基于电谐振单元的超介质吸波材料及矩形波导匹配终端应用研究*

李建 文光俊 黄勇军 王平 孙元华

(电子科技大学通信与信息工程学院,光纤传感与通信教育部重点实验室,成都 611731)

(2012年11月20日收到;2012年12月20日收到修改稿)

1 引言

超介质(metamaterial)是指一种自然界不存在的人工合成材料.1968年,前苏联科学家Veselago[1]理论分析了电磁波在介电常数ε(ω)和磁导率µ(ω)同时为负的各向同性均匀超介质中的电动力学行为,并预见了该类材料具有常规材料所不具有的一些独特电磁特性,如逆折射效应、逆多普勒频移效应、逆切连科夫辐射、负光压等.2000年,美国加州大学圣迭戈分校Smith等[2]采用金属导体线和金属谐振环相重叠的微结构为基本单元,首次人工合成出X波段超介质,同年英国帝国理工学院Pendry教授[3]提出了应用超介质实现完美透镜的可行性.2001年,Shelby等[4]通过实验测试证实了由Smith所设计的劈行二维超介质样品的负折射现象.这些研究成果开创了超介质的人工合成方法、机理、应用研究之先河,引起了国内外学者的极大研究兴趣,使超介质技术研究成为当今国际物理学界和电磁学界的前沿研究领域.

2000年始,超介质的研究主要集中在其实现机制探索[5-15]、奇异电磁特性分析[16-19]、应用研究[20-26]等方面.其中,基于超介质的吸波材料由于具有近理想的吸波性能而受到广泛关注[20-24].2008年,Landy等[27]首次研究实现了微波频段的基于电谐振环与短路金属线阵列的超介质吸波材料.随后,众多结构的超介质吸波材料被提出[28].其中,平面超介质吸波材料的主要实现结构为：在介质基板一面刻蚀出超介质金属谐振单元,另一面完全覆上金属.其吸波原理为：采用电谐振结构单负超介质实现电谐振特性,基于电谐振结构与介质层另一面的金属平板之间的耦合作用,将在金属平板上产生反向的表面电流,从而在金属谐振环与金属平板之间形成磁谐振.通过调节优化超介质的结构参数,使得其等效阻抗与自由空间波阻抗匹配,以及在匹配工作频段内具有高损耗特性(包括金属的欧姆损耗和介质的介电损耗),最终达到完美吸波特性.

另一方面,超介质吸波材料的实验测试方法主要为自用空间测试法,这种测试方法首先需制备大尺寸的测试样品,并采用两个喇叭天线在微波暗室里测试其反射系数(S11),最后得出超介质吸波材料的吸波率(A=1-|S11|2).这种测试方法的优点为可测试斜入射角以及不同极化角情况下的吸波性能,缺点是所需测试成本较高.2011年,西安电子科技大学李龙等[29]提出了可在矩形波导里测试小尺寸的超介质吸波材料,这种测试方法所需测试样品尺寸小,测试系统仅需一个波导同轴转换器以及矩形波导短路器.其缺点为不能测试超介质吸波材料在不同入射角和极化角情况下的吸波特性.但是,对于某些特定的应用环境,如本文要讨论的矩形波导匹配终端,采用矩形波导测试方法将具有其重要的研究价值.本文采用矩形波导测试方法,实验研究4种基于电谐振单元的超介质吸波材料的吸波性能,并分析将其作为矩形波导匹配终端时的各种指标特性.

2 基于电谐振单元的超介质吸波材料实验研究

2.1 实验样品加工及测试系统搭建

本文采用的4种电谐振单元如图1所示,其中第1种电谐振单元为参考文献[30]中所提出的树枝状谐振单元,第2种至第4种谐振单元为参考文献[31]中所设计的几种谐振单元.此4种单元结构均具有高度对称特性,因此由其构成的吸波材料具有极化不敏感特性.本文直接研究由这4种电谐振单元构成的吸波材料在X波段(8—12 GHz)矩形波导(WR90)中的吸波性能.

首先,根据X波段矩形波导的横截面尺寸(22.86 mm×10.16 mm)及其工作频段,采用商用电磁仿真软件(Ansoft HFSS 14.0)仿真优化本文所讨论的4种超介质吸波材料电谐振单元的结构尺寸.仿真模型如图2(a)所示,超介质吸波材料置于短路矩形波导的末端,矩形波导另一端设置为波端口.为便于实验测试验证,本文所采用的介质材料为FR4板材,其相对介电常数εr=4.0,介质损耗角正切值tanδ=0.02.FR4板材厚度0.8 mm,构成吸波材料的金属谐振单元以及FR4板材另一面的金属层为0.018 mm的金属铜(电导率为5.813×107S/m).基于上述材料及结构参数的限制,优化得出在矩形波导里具有近理想吸波特性的4种超介质吸波材料谐振单元尺寸(如图1中第二列所示,图中尺寸单位为mm).根据仿真优化得出的结构参数值,采用电路板刻蚀加工技术,制作出了如图1中第三列所示的4种超介质吸波材料样品.其中,第1种超介质吸波材料谐振单元间间隔为7.5 mm,第2及第3种谐振单元间间隔为5.0 mm,第4种谐振单元间间隔为4.8 mm.

图1 4种超介质吸波材料电谐振单元示意图和仿真优化出的结构参数值,以及制备出的对应超介质吸波材料样品

为测试超介质吸波材料在矩形波导里的吸波性能,本文采用一个工作于X波段的波导同轴转换器、一个短路器以及安捷伦矢量网络分析仪(Agilent N5230A)以搭建测试系统(如图2(b)所示).首先将超介质吸波材料样品置于波导同轴转换器的波导端口处,然后将短路器覆盖在波导端口处以防止电磁波能量泄漏,影响测试结果.最后将波导同轴转换器的同轴端口与矢量网络分析仪连接,测试其反射系数.

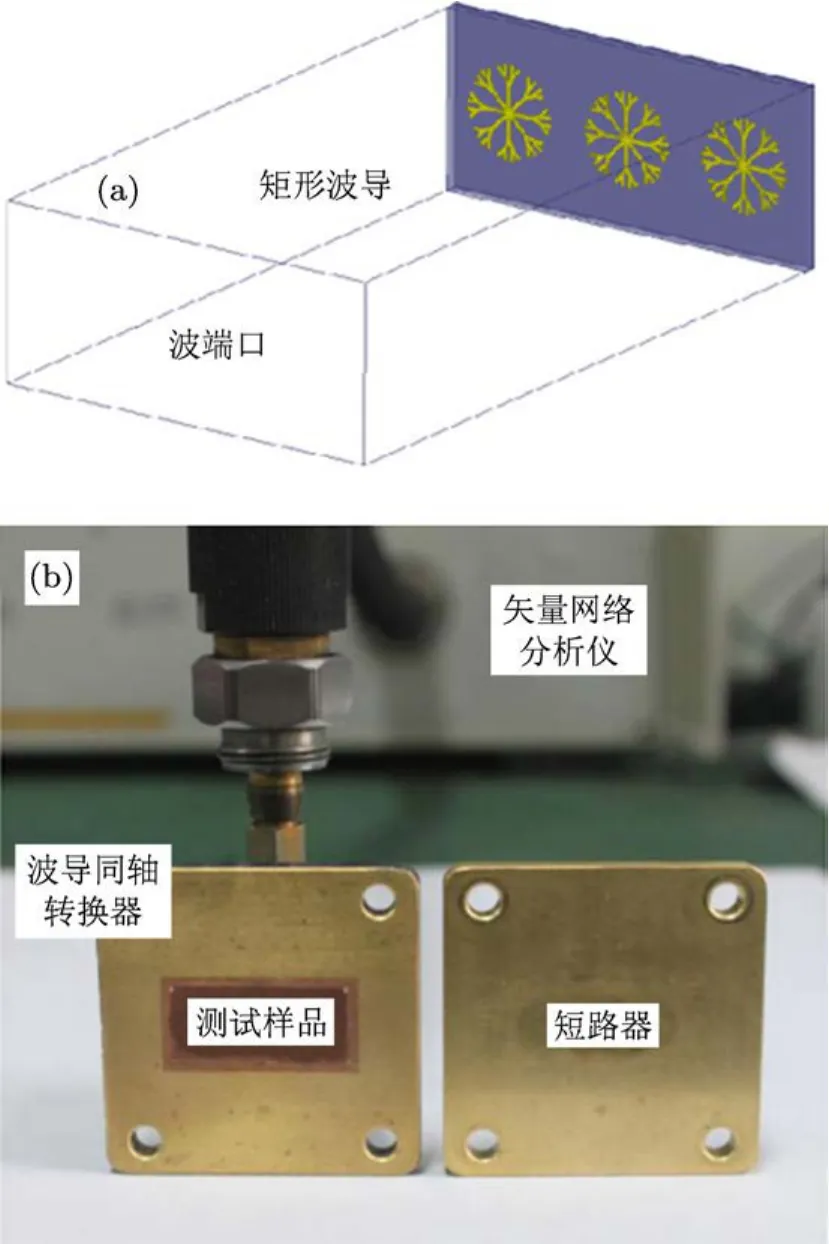
图2 置于矩形波导里的超介质吸波材料仿真及测试系统 (a)仿真模型;(b)测试系统

2.2 实验结果分析

采用上述测试系统,分别对本文所讨论的4种超介质吸波材料在矩形波导里的吸波性能进行测试,测试结果与相应仿真优化得出的数值结果如图3所示.其中反射率计算公式为为仿真/测试得出的反射系数值;由于在仿真及测试过程中,波导同轴转换器的波导端口被短路,因此没有电磁波能量泄漏,从而得出吸波率计算公式为A(ω)=1-R(ω)=1-|S11|2.由图3可知,本文所讨论的4种超介质吸波材料在矩形波导里均显示出了近理想的吸波性能.图3(a)所示为基于树枝状电谐振单元的超介质吸波材料的吸波特性,测试结果显示该种结构吸波材料的吸波峰值为99.4%(10.84 GHz),仿真所得吸波峰值为99.7%(10.68 GHz).测试与仿真所得吸波峰值基本符合,吸波峰值频率有一定频率偏移,由分析可知,该频移为实际加工误差所致.图3中其余3种结构超介质吸波材料的测试与仿真结果显示了相似的特性,此3种吸波材料的测试吸波峰值分别为97.3%(10.77 GHz),96.0%(10.51 GHz),97.2%(11.05 GHz);仿真所得结果分别为99.6%(10.69 GHz),93.8%(10.62 GHz),96.5%(10.95 GHz).

图3 本文所讨论的4种超介质吸波材料在矩形波导里的反射率及吸波率结果 (a)第1种吸波材料;(b)第2种吸波材料;(c)第3种吸波材料;(d)第4种吸波材料

图4所示为本文所讨论的4种超介质吸波材料的电谐振单元以及介质另一面的金属平板在吸收峰值频点处的表面电流分布仿真结果.由图可知,在矩形波导里实现的超介质吸波材料的表面电流分布与其在自由空间中的结果[30]类似.例如,图4(a)中的树枝状谐振结构的表面电流分布满足轴对称特性,因此能够实现典型的电谐振特性;而金属平板上面的表面电流与树枝状谐振结构的表面电流呈反对称特性,因此能在金属谐振环和金属平板之间形成磁谐振特性,此种谐振特点与文献[30]中分析的一致.图4中其余3种超介质吸波材料的表面电流特性与第一种结构类似.

图4 本文所讨论的4种超介质吸波材料的金属谐振单元以及介质另一面金属平板上的表面电流分布特性 (a)第1种吸波材料;(b)第2种吸波材料;(c)第3种吸波材料;(d)第4种吸波材料

由此可知,本文所讨论的在矩形波导里实现的4种超介质吸波材料具有与其在自由空间中相似的近理想吸波性能.因此,此种矩形波导测试研究方法可适用于其他已经提出的各种结构微波频段超介质吸波材料,以及可用于实验测试验证新提出的各种微波频段超介质吸波材料的吸波性能.

3 基于超介质吸波材料的匹配终端应用研究

由上一节分析可知,矩形波导加载超介质吸波材料可以实现一定带宽的吸波作用,且该种结构的反射系数趋近于零,因此,可将这种结构用于设计矩形波导匹配终端(其基本结构如图2(a)所示),以实现近完美的阻抗匹配特性.本文基于对加载超介质吸波材料的矩形波导的实验测试及仿真研究结果,得出所讨论的4种结构的电压驻波比特性以及阻抗Smith圆图特性如图5所示.由图可知,第1种及第2种超介质吸波材料加载的矩形波导匹配终端的电压驻波比特性在相应频段内显示出了较好的匹配特性,第3种超介质吸波材料加载的矩形波导匹配终端在其吸波工作频段内未能很好地达到匹配,第4种超介质吸波材料加载的矩形波导匹配终端表现出一定的匹配带宽.该4种超介质吸波材料加载的矩形波导匹配终端的最佳匹配点VSWR值,VSWR≤1.5的工作频段如表1所示,其中第2列及第3列为测试结果,第4列及第5列为相应的仿真结果.为进一步优化矩形波导匹配终端的匹配性能,可通过简单地调节介质基板的厚度来实现,其调节优化方法类似于吸波材料的优化方法[28].因此,本文所讨论的4种超介质吸波材料完全可用于设计矩形波导匹配终端,达到近理想的阻抗匹配性能.为进一步展宽此种匹配终端的工作带宽,可简单地通过加载宽带超介质吸波材料[32]实现.

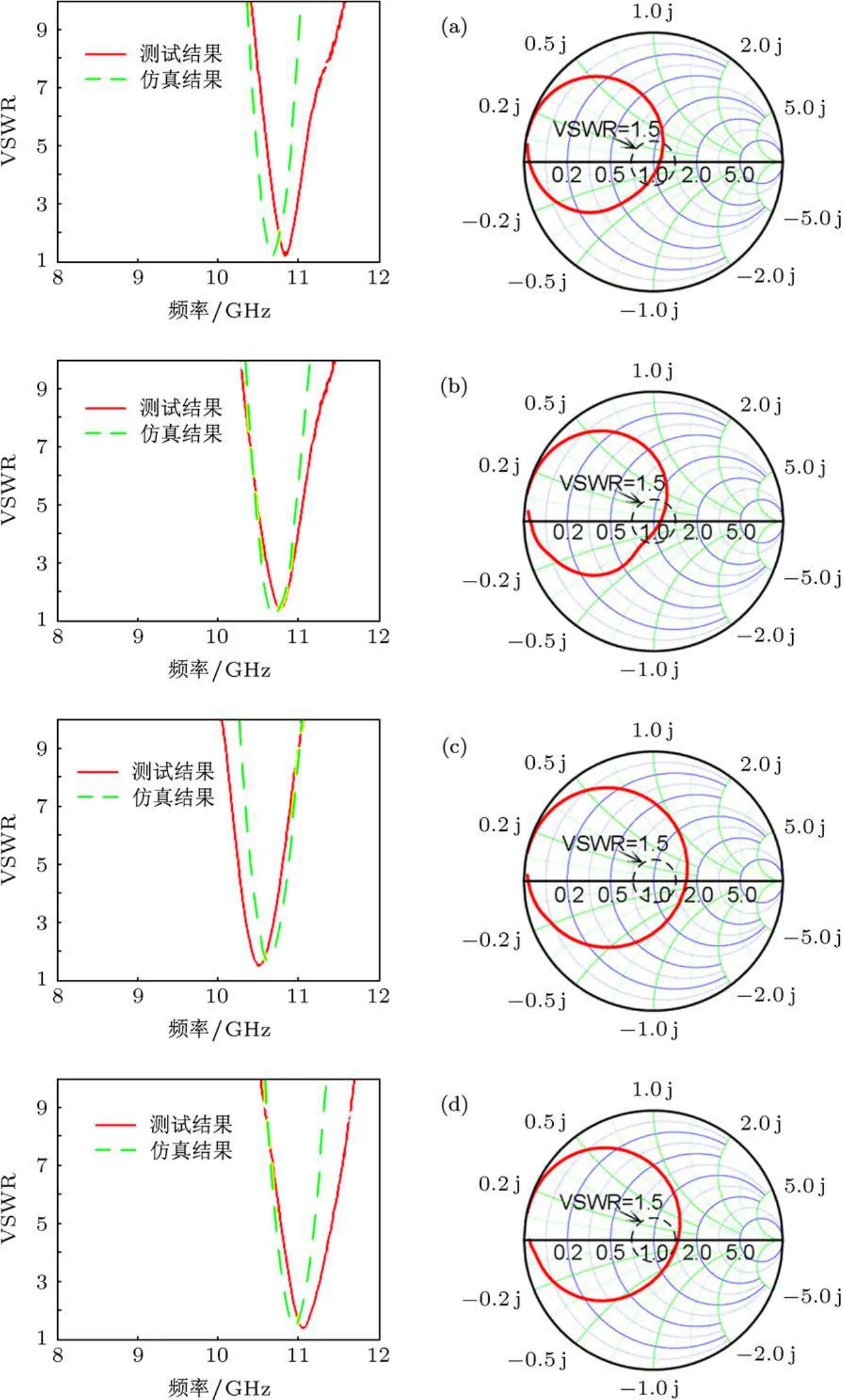
图5 4种超介质吸波材料加载的矩形波导匹配终端的电压驻波比(VSWR)以及阻抗Smith圆图特性

表1 4种超介质吸波材料加载的矩形波导匹配终端的测试与仿真结果

4 结论

本文采用矩形波导测试系统,实验与仿真相结合研究了4种超介质吸波材料的吸波性能及吸波机理.结果显示,超介质吸波材料在矩形波导中的吸波性能及吸波机理与自由空间中类似,因此得出矩形波导测试系统可用于其他新型超介质吸波材料的实验研究.进一步讨论了将超介质吸波材料加载到终端短路的矩形波导中,以实现窄带的匹配终端应用,结果显示该种新型的矩形波导匹配终端具有近理想的匹配性能,且其阻抗匹配带宽可通过设计宽带超介质吸波材料展宽.本文所讨论的超介质吸波材料测试方法及其矩形波导匹配终端应用具有重要的应用前景,可实现宽带小型化高性能的阻抗匹配终端.

[1]Veselago V G 1968 Sov.Phys.Usp.10 509

[2]Smith D R,Padilla W J,Vier D C,Nemat-Nasser SC,Schultz S 2000 Phys.Rev.Lett.84 4184

[3]Pendry JB 2000 Phys.Rev.Lett.85 3966

[4]Shelby RA,Smith D R,Schultz S 2001 Science 292 77

[5]Chen CH,Qu SB,Wang JF,Ma F,Wang X H,Xu Z 2011 Chin.Phys.B 20 034101

[6]Yang Y M,Wang JF,Xia S,Bai P,Li Z,Wang J,Xu Z,Qu SB 2011 Chin.Phys.B 20 014101

[7]Lu W B,Ji Z F 2011 Chin.Phys.B 20 054101

[8]Li J,Yang FQ,Wang Z,Dong JF 2011 Acta Phys.Sin.60 114101(in Chinese)[李杰,杨方清,王战,董建峰2011物理学报60 114101]

[9]Zhong J,Huang Y,Wen G,Sun H,Gordon O,Zhu W 2012 IEEE Antenn.Wireless Propag.Lett.11 803

[10]Huang Y J,Wen GJ,Li TQ,Li L W,Xie K 2012 IEEEAntenn.Wireless Propag.Lett.11 264

[11]Zang Y Z,He M X,Gu JQ,Tian Z,Han JG 2012 Chin.Phys.B 21 117802

[12]Xiong H,Hong J S,Jin D L,Zhang Z M 2012 Chin.Phys.B 21 094101

[13]Su Y Y,Gong B Y,Zhao X P 2012 Acta Phys.Sin.61 084102(in Chinese)[苏妍妍,龚伯仪,赵晓鹏2012物理学报61 084102]

[14]Liu Y H,Liu H,Zhao X P 2012 Acta Phys.Sin.61 084103(in Chinese)[刘亚红,刘辉,赵晓鹏2012物理学报61 084103]

[15]Xu X H,Xiao SQ,Gan Y H,Fu CF,Wang B Z 2012 Acta Phys.Sin.61 124103(in Chinese)[徐新河,肖绍球,甘月红,付崇芳,王秉中2012物理学报61 124103]

[16]Fan J,Sun G Y,Zhu WR 2011 Chin.Phys.B 20 114101

[17]Shi Y L,Zhou Q L,Liu W,Zhao D M,Li L,Zhang CL 2011 Chin.Phys.B 20 094102

[18]Zhou Q L,Shi Y L,Wang A H,Li L,Zhang CL 2012 Chin.Phys.B 21 058701

[19]Chen L T,Cheng Y Z,Nie Y,Gong R Z 2012 Acta Phys.Sin.61 094203(in Chinese)[陈龙天,程用志,聂彦,龚荣洲2012物理学报61 094203]

[20]Gu C,Qu SB,Pei Z B,Xu Z,Liu J,Gu W 2011 Chin.Phys.B 20 017801

[21]Gu C,Qu SB,Pei Z B,Xu Z 2011 Chin.Phys.B 20 037801

[22]Zhu W,Huang Y,Rukhlenko I D,Wen G,Premaratne M 2012 Opt.Express20 6616

[23]Yang Y J,Huang Y J,Wen GJ,Zhong JP,Sun H B,Gordon O 2012 Chin.Phys.B 21 038501

[24]Huang Y J,Wen G J,Li J,Zhong JP,Wang PSun Y H,Gordon O,Zhu WR 2012 Chin.Phys.B 21 117801

[25]Zhu W,Premaratne M,Huang Y 2012 J Electromag Waves Appl.26 2315

[26]Xu H X,Wang G M,Liang JG,Peng Q 2012 Acta Phys.Sin.61 074101(in Chinese)[许河秀,王光明,梁建刚,彭清2012物理学报61 074101]

[27]Landy N I,Sajuyigbe S,Mock JJ,Smith D R,Padilla WJ2008 Phys.Rev.Lett.100 207402

[28]Watts CM,Liu X,Padilla WJ2012 Adv.Mater.24 OP98

[29]Li L,Yang Y,Liang C 2011 J.Appl.Phys.110 063802

[30]Zhu W,Zhao X 2009 J.Opt.Soc.Am.B 26 2382

[31]Padilla WJ,Aronsson M T,Highstrete C,Lee M,Taylor A J,Averitt RD 2007 Phys.Rev.B 75 041102

[32]Ding F,Cui Y,Ge X,Jin X,He S 2012 Appl.Phys.Lett.100 103506