葛林森弧齿锥齿轮的有限元模态分析①

慕 灿， 陈 科

(1.阜阳职业技术学院，工程科技学院，安徽 阜阳 236016;2.合肥工业大学机械与汽车工程学院，安徽 合肥 230009)

0 引言

1913年格林森公司发明了曲线齿锥齿轮加工机床，宣告了弧齿锥齿轮的诞生.自20世纪60年代开始，格林森公司的弧齿锥齿轮生产技术日臻成熟，逐渐形成了一整套比较完善的设计和加工技术[1～4]，从而奠定了格林森公司在国际锥齿轮制造业中的主导地位.

弧齿锥齿轮具有承载能力强、重合度大、传动平稳等优点，在高速传动时能显著减少噪声和振动，可获得很大的传动比，对安装误差敏感性小，因此在航空、航天、工程机械等机械领域应用广泛.由于弧齿锥齿轮的几何形状、加工机床调整非常复杂，为了加速推广其在各个机械行业的应用，缩短生产周期，降低生产成本，进一步提高其使用性能，完善弧齿锥齿轮理论，近年来国内外学者运用现代技术继续开展了大量的研究工作.Gosselin[5]等推导出了弧齿锥齿轮载荷分配系数以及传动误差的通用计算公式，Bibelt[6]、Fuents[7]等使用有限元分析方法对弧齿锥齿轮的接触应力进行了仿真分析，Litvin[8]教授等采用有限元模拟仿真和物理实验相结合的方法，研究了低噪音高强度弧齿锥齿轮的设计、制造和应力分析，李源等[9]采用 MSC.Mare有限元软件分析了航空螺旋锥齿轮的啮合过程.李盛鹏等[10]采用ANSYS软件对弧齿锥齿轮进行了接触分析.

弧齿锥齿轮用于高速、高载荷、大转矩等工况时，齿轮副不仅产生复杂的接触应力，而且在激励力的作用下会产生机械振动，当激励力频率与齿轮副的固有频率接近时将产生共振，不仅出现严重的噪声，齿轮副也可能受损甚至彻底失效.模态分析可以帮助设计人员确定结构的固有频率和振型，从而消除共振、降低噪声，并指导工程师预测在不同载荷作用下结构的振动形式.近年，已有学者[11，12]结合三维CAD和有限元分析软件计算了各种圆柱齿轮的固有频率和振型，但有关结构十分复杂的格林森弧齿锥齿轮的动力学模态分析的文献则较少.本文在UG NX中利用参数化设计方法直接由其内部驱动程序生成格林森弧齿锥齿轮，然后将齿轮模型导入ANSYS Workbench中进行模态分析以得到其低阶固有频率和振型，在此基础上讨论弧齿锥齿轮的主要结构参数对固有频率的影响规律，为弧齿锥齿轮的结构优化、噪音控制及进一步动力学研究打下了基础.

1 模态分析的理论基础

模态分析是计算结构振动特性的数值技术，结构振动特性包括固有频率和振型.模态分析是其他动力学分析的基础，如响应谱分析、随机振动分析、谐响应分析等都需要在它的基础上进行.根据弹性力学有限元法，由达朗贝尔原理可得齿轮系统的运动微分方程为:

式中，[M]，[C]，[K]分别为质量矩阵、阻尼矩阵和刚度矩阵，{X}分别为加速度向量、速度向量和位移向量，{X}={X1，X2，…，Xn}T;{F(t)}为激振力向量，{F(t)}={f1，f2，…，fn}T.

在无阻尼自由振动情况下阻尼力项和外界激振力项为零，其运动微分方程为:

其对应的特征方程为

式中，ωi为系统的固有频率，φi为系统模态振型，i=1，2，…，n.

2 格林森弧齿锥齿轮有限元模态分析

2.1 格林森弧齿锥齿轮实体模型的建立

以一个汽车后桥主减速器中格林森弧齿锥齿轮(主动轮，等顶隙收缩齿)作为研究对象.其主要几何尺寸参数如表1所示.使用UG NX中GC工具箱的齿轮建模命令实现齿轮参数化建模，在齿轮参数对话框中对应输入大端模数、齿数、齿宽、法向压力角、旋向和中点螺旋角等，即可得到格林森弧齿锥齿轮的实体模型，再使用UG NX的“孔”命令增加轴孔即可，如图1所示.

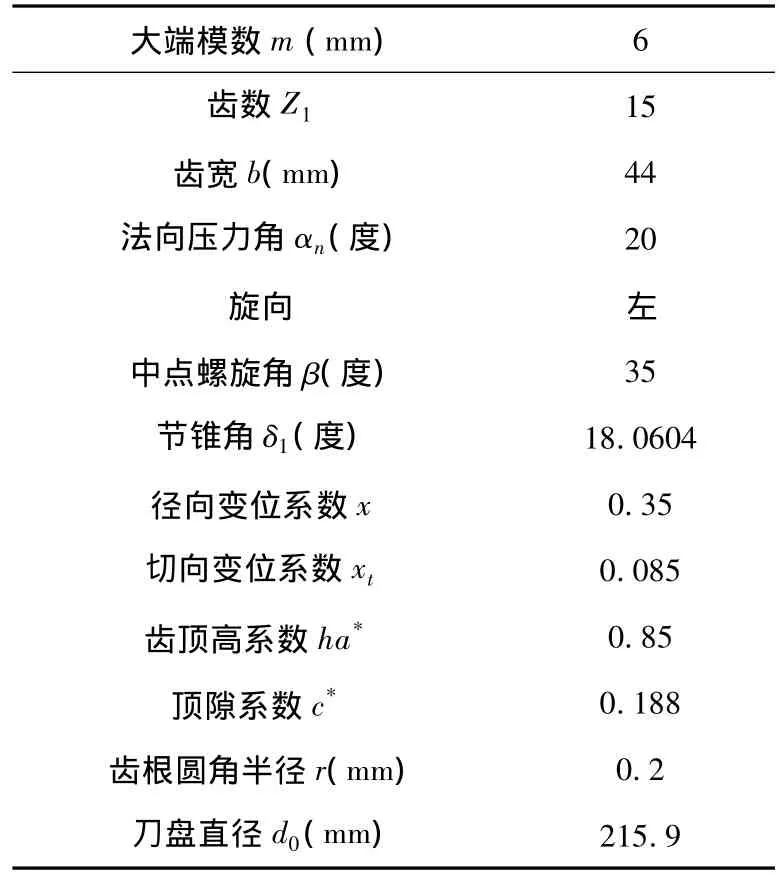
表1 齿轮设计几何参数

2.2 格林森弧齿锥齿轮有限元模型的建立

打开ANSYS workbench，从工具箱中拖放modal到项目视图区建立一个模态分析系统，将用UG NX建立的齿轮实体模型导入geometry模块，接着双击Model进入模态分析界面.编辑材料属性如下:弹性模量 EX=2.0675e8，泊松比 PRXY=0.3，密度 DENS=7.85e－6.设定目标物理环境为CFD，可获得质量较高、平滑过渡的网格.设定最小单元尺寸为3mm，经反复测验，精度能满足要求.因为格林森弧齿锥齿轮的齿面为复杂的空间曲面，这里采用自动网格划分方式，求解后查看划分结果情况:单元类型为Linear Tetrahedron，8144个节点，38584个单元，网格划分质量较好，如图2所示.

图1 格林森弧齿锥齿轮实体模型

图2 齿轮有限元模型

2.3 计算结果分析

添加边界条件并设定提取模态阶数.在典型的模态分析中唯一有效的载荷是零位移约束，其它的载荷形式均被忽略，因此仅在齿轮轴孔施加零位移约束.模态分析时因低阶模态刚度相对较弱，对于运动起主导作用，一般只需提取5～10阶即可满足精度要求，文中提取前10阶固有频率.

图3 模数－固有频率变化曲线

图4 齿数－固有频率变化曲线

图5 螺旋角－固有频率变化曲线

求解并查看结果.求解完毕后使用 ANSYS Workbench后处理工具得到弧齿锥齿轮的前6阶固有频率如表2所示.从表中可以看出，固有频率随着阶次的增加逐渐增大;由于齿轮结构近似对称，2和3阶、5和6阶、7和8阶、9和10阶的固有频率基本相同.

图6 径向变位系数－固有频率变化曲线

图7 切向变位系数－固有频率变化曲线

表2 齿轮前10阶固有频率

3 齿轮参数对固有频率的影响规律

3.1 模数的影响规律

在齿轮其它参数均保持不变的情况下，分别计算模数 m=4，6，8，10，12 五种情况下的前 10 阶固有频率，略去因结构和约束对称频率相近的第二、六、八和十阶(以下同)，其余各阶如图3所示.由图可见，齿轮固有频率随模数的增大而减小，而且影响较为显著.

3.2 齿数的影响规律

在齿轮其它参数均保持不变的情况下，分别计算齿数z=12，15，18，21和24五种情况下的固有频率，如图4所示.由曲线可以看出，固有频率随齿数的增大而减小.

3.3 螺旋角的影响规律

在齿轮其它参数均保持不变的情况下，分别取中点螺旋角 β =30°，32.5°，35°，37.5°和 40°建立五个齿轮模型，计算所得齿轮的固有频率随中点螺旋角的变化曲线如图5所示.由图可见，齿轮的固有频率随着螺旋角的加大而变化不明显.

3.4 径向变位系数的影响规律

在齿轮其它参数均保持不变的情况下，分别取径向变位系数 x=0.3，0.35，0.4，0.45 和0.5 建立五个齿轮模型，计算所得齿轮的固有频率随径向变位系数的变化曲线如图6所示.由图可见，轮齿的固有频率随着径向变位系数的加大而略有降低.

3.5 切向变位系数的影响规律

在齿轮其它参数均保持不变的情况下，分别计算切向变位系数 xt=0.06，0.085，0.11，0.135 和0.16五种情况下的固有频率，如图7所示.可以看出，切向变位系数对齿轮固有频率的影响与径向变位系数相当，并不十分明显.

4 结论

(1)利用UG NX中GC工具箱的齿轮建模功能可高效建立格林森弧齿锥齿轮实体模型，大大缩短了齿轮设计的时间;同时利用UG NX与ANSYS Workbench之间的数据接口，将齿轮模型精确地导入ANSYS Workbench中，弥补了ANSYS的建模功能的不足，提高了设计的效率.

(2)通过改变格林森弧齿锥齿轮的设计参数(包括模数、齿数、螺旋角、径向变位系数和切向变位系数)，得出了不同参数情况下固有频率的变化规律.分析结果表明，随着模数和齿数的增加，齿轮的固有频率明显减小，而中点螺旋角、径向变位系数和切向变位系数的增加将使齿轮的固有频率略有减小，但影响并不十分明显.

(3)齿轮的有限元模态分析结果为格林森弧齿锥齿轮的结构设计和进一步动力学研究提供了理论基础，同时为齿轮的结构优化和噪音控制提供了参考依据.

[1]The Gleason Works.Method for Designing Hypoid Gear Blanks[M].Rochester，New York:Gleason Work，1971.

[2]The Gleason Works.Calculating Instructions Generated Hypoid Gears[M].Rochester，New York:Gleason Work，1971.

[3]The Gleason Works.Calculating Instructions Formate Hypoid Gears[M].Rochester，New York:Gleason Work，1971.

[4]The Gleason Works.Calculating Instructions Formate Spiral Bevel Gears[M].Rochester，New York:Gleason Work，1971.

[5]Gosselin C，loutier L，Nguyen QD.A General Formulation for the Calculation of the Load Sharing and Transmission Error under Load of Spiral Bevel and Hypoid Gears[J].Mechanism and Machine Theory，1995，30(3):433 －450.

[6]Bibel GD，Kumar A，Reddy S，et.a1.Contact Stress Analysis of Spiral Bevel Gears Using Finite Element Analysis[J].ASME Journal of Mechanical Design，1995，117(2A):235 －240.

[7]Fuentes A，Litvin FL，Mullins BR，et.a1.Design and Stress Analysis of Low－Noise Adjusted Bearing Contact Spiral Bevel Gears[J].ASME Journal of Mechanical Design，2002，124(2A):524－532.

[8]Litvin FL，Fuentes A，Hayasaka K.Design，Manufacture，Stress Analysis，and Experimental Tests of Low － Noise High Endurance Spiral Bevel Gears[J]，Mechanism and Machine Theory，2006，41(1):83－118.

[9]李源.航空减速器螺旋锥齿轮啮合仿真分析[D].长沙:国防科学技术大学，2005.

[10]李盛鹏.弧齿锥齿轮动频率计算及接触分析研究[D].西安:西北工业大学，2006.

[11]吴卓，刘广利.基于PRO/E与ANSYS渐开线直齿圆柱齿轮模态分析[J].科学技术与工程，2009，(18):5476 －5478.

[12]李强，何家宁，张伟.基于Pro/E和ANSYS的渐开线圆弧齿轮模态分析[J].科学技术与工程，2011，(19):4447.