关于不定方程x2＋y2＋p＝xyz解的探讨

管训贵

（泰州师范高等专科学校 数理信息学院，江苏 泰州225300）

0 引言

长期以来，不定方程的求解是数论中引人关注的课题，很多数学家和数学爱好者对此做过大量的研究。［1－7］

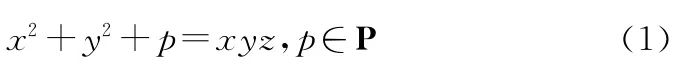
本文利用Fermat创立的无穷递降法研究了不定方程的正整数解问题，得出以下一般性的结果。用N＊，P分别表示全体正整数和全体奇素数的集合。

1 结果与讨论

定理1 设p∈P，p＋1＝ab（a，b∈N＊，且a＞1，b＞1），则不定方程（1）的全部正整数解为

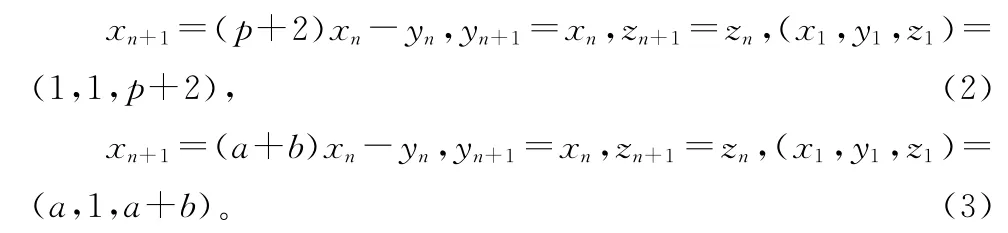
式中x与y可交换。

证明 设（1）的任一正整数解为（x，y，z）。由x，y的对称性可假定x≥y。

或

当（4）式成立时，代入（1）可知，r2t＝2r2＋p，即r2｜p，故r＝1，t＝p＋2。

当（5）式成立时，代入（1）可知，rt＝r2＋（p＋1），即r｜（p＋1）＝ab。若r＝1，则t＝p＋2，可归于（2）；若r＝p＋1，则t＝p＋2，由（2）知（x2，y2，z2）＝（p＋1，1，p＋2），仍可归于（2）。故r应为p＋1的真因数且r＞1，不妨设r＝a，则t＝a＋b。

综上所述，方程（1）的全部正整数解为（2）和（3），并且x与y可交换。

定理得证。

根据定理1直接可得如下推论（下文中Mp为Mersenne素数，Fn为Fermat素数）。

推论1 不定方程x2＋y2＋Mp＝xyz的全部正整数解为

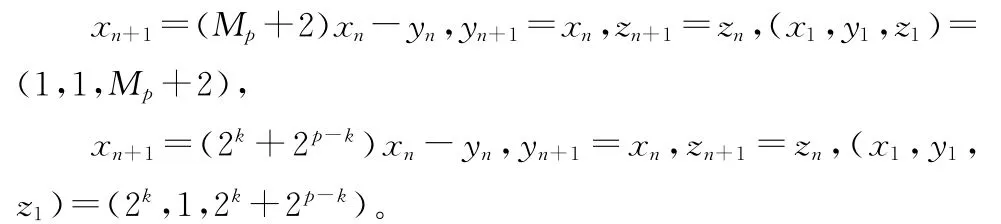
式中x与y可交换，1≤k≤p－1。

推论2 不定方程x2＋y2＋F0＝xyz的全部正整数解为

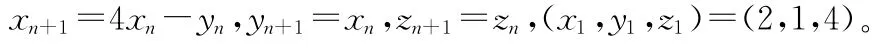
式中x与y可交换。

推论3 不定方程x2＋y2＋F1＝xyz的全部正整数解为

式中x与y可交换。

推论4 不定方程x2＋y2＋F2＝xyz的全部正整数解为

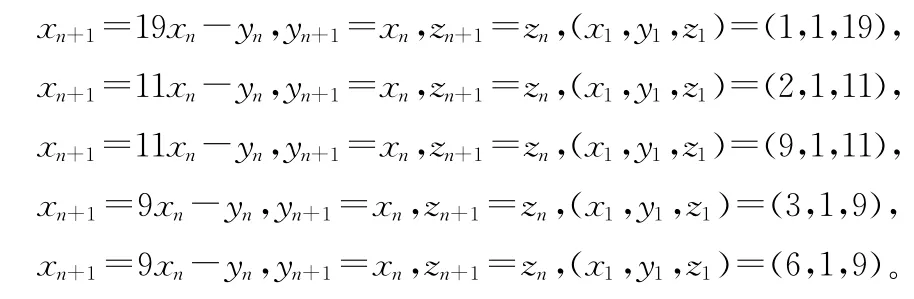
式中x与y可交换。

推论5 不定方程x2＋y2＋F3＝xyz的全部正整数解为

式中x与y可交换。

推论6 不定方程x2＋y2＋F4＝xyz的全部正整数解为

式中x与y可交换。

2 结语

本文的推论从另一角度给出了Mersenne素数与Fermat素数的表示方法，为研究Mersenne素数与Fermat素数开辟了一条全新的道路。

［1］ Mordell L J，Diophantine equation［M］．London：Academic Press，1969．

［2］ Guy R．Unsolved problems in Number Theory［M］．New York：Springer Verlay，2004．

［3］ 柯召，孙琦．谈谈不定方程［M］．上海：上海教育出版社，1980．

［4］ 管训贵．不定方程x2＋y2＋z2＝2（xy＋yz＋zx）［J］．齐齐哈尔大学学报：自然科学版，2012，28（1）：89－91．

［5］ 周泽文．关于不定方程ax2＋y2＋z2＝axyz（a∈N＊）［J］．高等函授学报：自然科学版，2004，18（5）：23－25．

［6］ 杨小康．关于不定方程x2＋y2＋z2＝1＋dxyz［J］．齐齐哈尔大学学报：自然科学版，2010，26（6）：87－89．

［7］ 管训贵．不定方程x3＋y3＋z3－3xyz＝n有非负整数解的充要条件［J］．四川理工学院学报：自然科学版，2011，24（4）：389－392．