大型数控铣齿机振动测试及减振方案研究*

董维新 胡万良 李云霞

(陕西秦川机械发展股份有限公司，陕西宝鸡 721009)

大型数控铣齿机是在传统的铣齿机基础上发展起来的，作为大型、高速、高精度的数控机床，其工作性能指标要求也大大提高.比如，作为一台自动化的机床，为了保证机床在各种工况下的加工稳定性，不仅要求机床结构具有良好的静态特性，而且更要具有良好的动态特性。

国内外学者针对机械结构的静动态设计进行了广泛深入的研究，取得了大量的成果［1－9］。例如，早在上世纪80 年代初，Cleek，A.L.和 Pacelic，V.对数控加工中心进行了结构频率响应以及模态分析，总结出机床的动态特性是决定其结构性能的重要因素，利用测量装置得出了系统的频率响应特性和振型。

本文针对某大型数控铣齿机动态性能、提高加工精度等问题，参考国内外相关研究方法，考察其在实际切削过程中，面临各种外界干扰以及静态或动态力的作用下，机床将会出现哪些振动响应，是否影响加工精度，是否影响到切削加工无法继续进行，继而进行进一步的动力学分析，看是否可以找到其成因，为提高机床整体动态性能，减小振动提供依据。

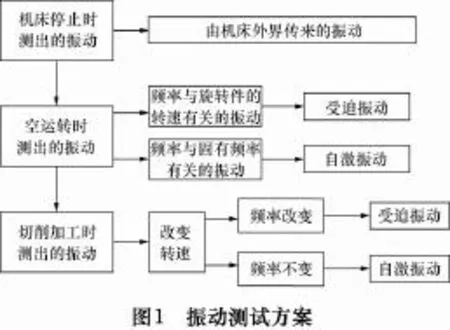
1 振动测试方案

机床加工中出现的振动按原因可分为自由振动、受迫振动、自激振动3种［9－11］。对于精密机床，应在保证加工质量的前提下考虑切削效率;相反，对于粗加工机床，应在保证切削效率的前提下考虑加工质量;对于普通机床以及目前正在发展的粗精加工都能使用的机床，应两者兼顾。切削过程中的振动较为复杂，是各种振动因素的叠加。因此，对机械系统进行振动测试，找出响应振源并改进机械振动系统，可以达到减振提高加工质量的目的。

如图1所示，对机床进行切削振动测试，可以判别出振动的类型。首先对机床停止时的外界干扰引起的振动进行测量，再测出空转时的振动。对于频率与各旋转件的转速有关的振动，就可以认为是其中的受迫振动。对于频率与转速无关而与机床各零、部件的固有频率有关的振动，就可认为是其中的自激振动。

2 切削试验

图2为数控铣齿机整机装配图，为找出切削加工中各振动量的大小及振源，分别对各转速调试过程中的铣齿机进行了停机测试试验、空转试验以及切削试验。测试的重点是刀架系统，因为它是加工系统的最主要部分，其与工件直接接触，最终影响加工精度。刀架双摆结构的测点布置如图3所示。

机床双摆结构为多轴联动结构，为详细测试出双摆结构各个部分的振动量大小以找出主要振动来源，在每个部件上X、Y、Z方向上均布置传感器。测试系统中单向传感器11个(布置于双摆上)，三向传感器1个(布置于工件正对切削位置)，共占用14个通道。现场测试模型如图4所示。

按测点号连接好传感器和仪器，根据灵敏度及增益标定各个通道后。进行采样示波，调整各通道输入输出的增益大小，使信号不致过大超过量程或过小，以防有效信号分辨率低。根据理论分析得到的前六阶固有频率的频率范围，设定分析频率为500 Hz。

2.1 停机测试

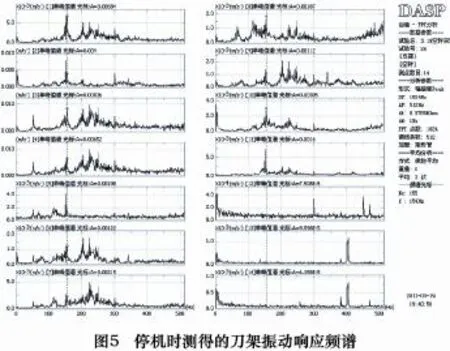
进行停机测试试验可以找出机床的外部振源，例如经过地基传来的振动、电磁干扰等。可以引起的振动形式有自由振动和受迫振动。首先采集时域信号，为分析其中各振动频率分布，对时域信号作自谱分析，得到响应频谱，如图5所示。

由图5响应频谱可以看出，台面响应较小。Y、Z方向在512 Hz内加速度响应幅值均在1×10－3m/s2以下，X方向则在4×10－3m/s2以下。而双摆结构上各测点的幅频特性曲线基本相近，响应幅值较大的3、4两测点加速度幅值范围在1×10－2m/s2以下。

由a=ω2x=(2πf)2x可得到由加速度到振动位移变换公式

式中:a为加速度;f为频率;w为角频率。

双摆上测点出现明显50 Hz峰值，分析其为交流电电磁力干扰。在3号测点出现最大峰值加速度0.006 m/s2，由式(1)计算出对应振动位移量6.09×10－5mm，振动位移很小。50 Hz以后出现不规则宽频激励，振动位移相比50 Hz时更小。综上可得出结论:外界干扰引起的振动量很小。

2.2 空运转试验

根据对机床振动类型的分析，该机床采用电主轴直接驱动刀具进行切削，排除传动链产生的振动。进行空转试验主要目的是为了测试出各种受迫振动振源的影响，受迫振动的可能因素有回转件的不平衡及空转启动中外部动力源，例如液压、气压系统引起的交变力等。

测试过程中气压驱动装置仍打开，采用同样的测点布置方案。精切加工转速为250 r/min。得到时域信号如图6所示。

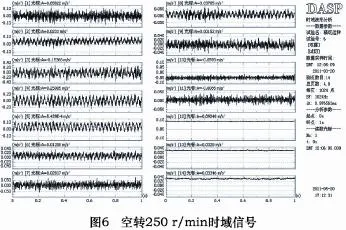
空运转测试时，工件及台面不受转速的影响，其响应同停机时一样。由时域信号可以看出，仍旧是3、4测点响应加速度值最大。对其进行频域内自谱分析得到峰值频率分布。由空转频谱可见在停机状态下的电磁干扰被湮没，也说明外界干扰相较自身转速激励而言可以忽略。双摆结构测点上具有明显的峰值响应，在3、4测点响应峰值相对较大。为详细分析各振动频率分量，对实验结果进行了自谱分析，如图7所示。

由频谱分析可以看出各测点具有相似的峰值频率，说明了测试的可靠性。其中靠近切削刀具的3号测点相较其他测点峰值更大，提取其频谱峰值加速度数据并按公式(1)计算得到其振动位移量见表1。

表1 空转转速250 r/min下振动频率及位移

由数据处理结果可见振动位移量最大值为频率4 Hz，位移大小为2.25×10－3mm。空转转速250 r/min对应频率为4.16 Hz，因数据分析频率分辨率为1 Hz，有理由认为4 Hz下的振动即为不平衡质量引起的受迫振动。且转速的微小跳动，其后的9 Hz可看作转速频率2倍频，且21 Hz、33Hz等都与转速频率有倍数关系。可进一步得出结论:振动来源于主轴系统不平衡引起的受迫振动。

2.3 切削试验

切削过程中采用气动驱动，主轴变频器在切削转速250 r/min下频率为12.5 Hz。测试时采用铣削加工，常用进给量为50 mm/min。铣削切屑刀片数为4，据转速得刀具断续切削引起的激励频率为16.67 Hz。

选取试验号2的时域信号进行分析，如图8所示。可以看出，相比停机和空转时响应加速度值明显提高很多。且台面振动响应也有所提高，相比双摆结构上的测点而言响应仍较小。同前一样，3、4号测点响应加速度值最大。振动加速度范围为±2 m/s2，其他测点在±1 m/s2以内。

为得出具体峰值频率分布，对其进行自谱分析，如图9所示。由全部14个通道分析结果可以明显看出各频谱具有很好的相似性，说明了测试结果的可靠性。台面和双摆结构上测点也具有基本相同的峰值分布，可见在切削加工时双摆部分和台面部分相互作用，各结构部件组成切削系统。

频谱中出现明显的峰值频率，且14个通道测点的频谱中的峰值频率分布基本一致。对比发现，台面峰值响应相对双摆结构上的响应差3个数量级，相比双摆小得多。

切削试切过程中，在加工小曲率位置时进给量为50 mm/min，而在加工齿轮曲面拐点也即大曲率圆弧时为了切除较多材料进给量设定为68 mm/min。且现场可明显感觉到在加工大曲率圆弧时振动大。因此有必要对两数据进行对比分析，每组试验中均是3号测点响应峰值最大，2号试验为加工小曲率半径，对其进行数据处理，得到位移响应频率分布。

表2 加工小曲率位置振动频率及位移

由数据处理结果可以看出，位移最大幅值出现在17 Hz，切削激励频率。位移值为1.651 7×10－2。比空转时的振动位移高出一个数量级。其后出现的33 Hz、50 Hz为切削激励频率的倍频，振动位移与比17 Hz时低一个数量级。5号试验为加工大曲率半径，对其进行数据处理作对比分析，如表3所示。

由加工大曲率半径位置的分析结果，最大位移响应出现在16 Hz。因频率分辨率为1 Hz，且转速跳动的原因，仍可认为其为切削激励频率。在2倍频32 Hz的振动位移量也很大，在同一数量级。其后的倍频下振动位移则相对较小。

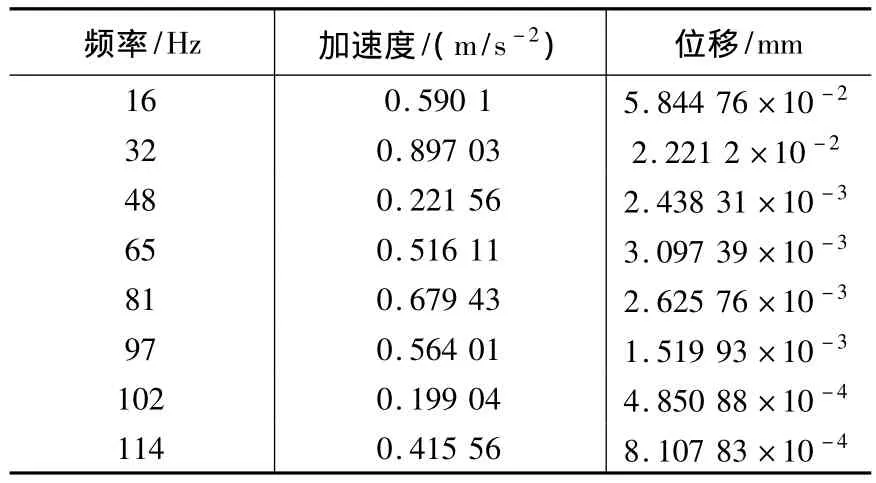
表3 加工大曲率位置振动频率及位移

3 试验结果分析

3.1 振动测试结论

在以上停机试验、空转试验及切削试验所有测试中均是3、4号测点振动位移最大，且两者加速度传感器方向同向。该两个测点对应的是刀架的最前端，刀架作为悬臂结构，该两个测点正好对应其最前端，同时也是最接近刀具加工区的位置。对比两者切削时域信号对比图如图10所示。

由时域信号可见3、4号测点出现明显峰值响应的频率基本是相同的。对比振动相位，既有同相位峰值也有相差180°左右的峰值，也即两测点有时同向达到最大位置，有时同时反向达到最大位移。由此判定电主轴部分的运动为既有平动，又有绕C2轴的扭转，因此对加工精度有很大影响。

如图11所示，对比各个频率下的不同工况振动位移量，在增大进给量加工大曲率位置时振动位移最大，是加工小曲率位置时振动位移的两倍以上，且两者的最大振动位移均出现在切削激励频率下。由空转振动幅值频率可以看出，主轴系统本身存在不平衡问题，但引起的受迫振动位移相对较小。

由测试结果可得出结论:外界干扰引起的振动很小;切削中工件未出现明显振纹，排除颤振的因素;根据前面对立柱部分的固有频率分析结果，说明切削激励频率在结构固有频率共振区外，综上也说明了切削系统设计的合理性;回转件不平衡引起的受迫振动相比切削激励引起的振动小;切削试验中产生的振动主要为切削激励下的受迫振动。

3.2 减振方案分析

根据上述分析，因主轴系统不平衡引起的振动幅值很小。影响较大的因素是切削刀具安装所出现的不平衡问题。可以通过重新调整安装来减小这一因素引起的振动量。

减小因断续切削激励引起的受迫振动的方法有:(1)改善结构设计，增大切削系统刚度;(2)设计隔振装置，提高系统结构等效阻尼;(3)提高切削转速或减小切削进给量，以减小切削力;(4)或改善加工工艺，改变切削力方向使其避开结构刚度薄弱方向。

对于前两种方案，对结构进行重新设计或增加隔振器，就要增加一定的生产成本，而且相关动力系统也需作相应改变。第三种方案中提高切削转速使刀具材料需要作相应的改变，也会一定程度上提高成本，而减小切削进给量必将影响加工效率。由于机床双摆结构可实现多轴联动，可通过软件程序调整加工各轴相对位置，对已在进行加工的机床，此该方案较为可行。

4 结语

本文分析了机床振动的形式。为找出振动来源，对机床切削过程分别进行了和切削试验。停机测试及空转实验结果表明外界干扰较小，在进行了切削试验后发现主轴系统存在不平衡问题，经过分析发现振动主要来源于主要振动来源于切削激励频率引起的受迫振动。在整个切削过程未出现明显振纹，从而可以排除颤振的因素，进一步说明了切削系统设计的合理性。在得到测试结果并对其进行分析的基础上，本文还提出了几种减振方案，并对方案进行了分析，为以后机床的振动控制提供了一定的依据。

［1］张波，陈天宁，虎恩典，等.数控车床分体式床身结合面参数优化识别及其动特性分析［J］.现代制造工程，2004(6).

［2］董凯夫.MK7132A数控卧轴矩台平面磨床的试验模态分析［D］.杭州:浙江工业大学，2008.

［3］大久保信行.机械模态分析［M］.上海:上海交通大学出版社，1985.

［4］大久保信行.模态分析发展综述［J］.机械研究，1985(1).

［5］李涛.MB4250－高精度立式桁磨机床的动态特性分析［D］.上海:上海交通大学，2008.

［6］Zaghbani I，Songmene V.Estimation of machine－tool dynamic parameters during machining operation through operational modal analysis［J］.International Journal of Machine Tools and Manufacture，2009，49(12 －13):947–957.

［7］Jiang T CM A.System approach to structural topology optimization:designing optimal connections［J］.Journal of Mechanical Design，1998，(12):619－621.

［8］Myers A.Finite element analysis of the structural dynamics of a vertical milling machine［M］.Laser Metrology and Machine Performance VI.WIT Press，Southampton，2003:431 －440.

［9］杨啸，唐恒龄，廖伯瑜.机床动力学(Ⅰ)［M］.北京:机械工业出版社，1993:110－115.

［10］杨啸，唐恒龄，廖伯瑜.机床动力学(Ⅱ)［M］.北京:机械工业出版社，1993:1－98.

［11］廖伯瑜，周新民，尹志宏.现代机械动力学及其工程应用——建模、分析、仿真、修改、控制、优化［M］.北京:机械工业出版社.2004.