基于VERICUT的指形铣刀数控加工等基圆锥齿轮仿真*＊1

王 斌 邓效忠 陈 均 李更更

(①西北工业大学机电学院，陕西西安 710072;②河南科技大学机电工程学院，河南洛阳 471003;③酒泉卫星发射中心，甘肃兰州 732750)

等基圆曲线齿锥齿轮是与格里森、奥利康等齿制不同的一种新型曲线齿锥齿轮［1］。通过控制刀具和轮坯的相对运动，使齿轮的螺旋角按特定规律变化，保证所加工的锥齿轮不同锥距处当量齿轮的基圆半径不变，即齿廓形状不变，从理论上保证了可以使用一把铣刀精确加工整个齿面［2］，而且根据需要可以设计成收缩齿或等高齿。其加工刀具结构简单、价格低廉，不需要专用机床，极大地降低了曲线齿锥齿轮的加工成本。对于需求量不大，但又要强度高、传动平稳、寿命长的大型相交轴运动，其尺寸大、难于用格里森、奥利康和克林根贝格机床加工，很适合于采用等基圆锥齿轮传动，如大型连续轧钢机、大型钻探机、大型圆锥破碎机等的锥齿轮［3］。

仿真加工是实际加工在虚拟环境下的映射，可对加工过程的各个环节进行评价和预测。VERICUT是CGTECH公司开发的数控加工仿真软件，具备同时进行刀具轨迹和机床运动仿真的功能，能够逼真地模拟数控加工仿真过程。利用VERICUT软件平台对等基圆锥齿轮进行的仿真加工国内鲜有报道。基于此，本文在VERICUT环境下，规划了刀具加工轨迹、计算了起刀点坐标、求解了凸凹面转换中轮坯的回转角度、建立了刀具模型、编写了数控加工的主程序和子程序，最终实现了对该齿轮的加工仿真。所选用的机床、夹具、刀具、刀杆等和实际加工中完全一致，加工过程中的运动情况清晰，可视性好，为普及推广等基圆锥齿轮的数控加工提供了实例。

1 等基圆锥齿轮基本原理

等基圆曲线齿锥齿轮任意锥距处当量齿轮的基圆半径为:

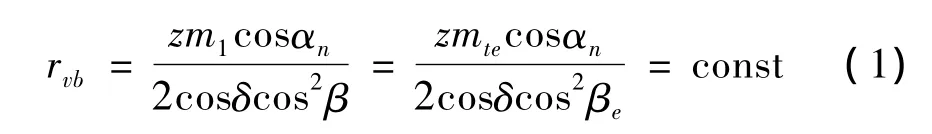
由式(1)得齿线的螺旋角β与锥距R的关系为

式中:z为锥齿轮齿数;δ为锥齿轮分度圆上的锥半角，(°);αn为齿廓法面压力角，(°);R、Re为分别为任意点锥距和大端锥距，mm;mt、mte为锥距为R、Re处的端面模数，mm;β、βe为对应于R、Re处的齿线螺旋角，(°)。

2 加工轨迹的规划

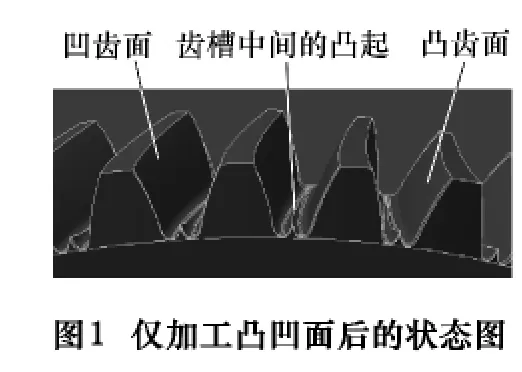
根据等基圆齿轮的理论［1］，在其齿面仿形加工中，一个齿槽的凸面和凹面至少要走刀一次，完成凸面和凹面的加工之后会在齿槽中间形成一个棱，如图1所示。所以至少还需要一次走刀，最终完成齿槽的加工，如图2所示。本次仿真加工中，规划3次走刀完成齿面、齿槽的加工。实际中为了齿槽的更规矩和更合理，走刀次数可适当调整。

等基圆锥齿轮加工中，刀具辅助坐标系在冠轮平

式(3)中:±中的“+”用于凹齿面，“－”用于凸齿面;r0理论齿线与其等距线之距离，由刀具尺寸确定，mm;s为沿理论齿线法向修形量，mm。式(4)中:±中的“+”用于右旋凹齿面或者左旋凸齿面，“－”用于右旋凸齿面或者左旋凹齿面;θ为理论齿线上锥距为R处的齿线极角;θd为理论齿线极径与刀具中心轨迹极径的夹角;根据文献［3］，在工件坐标系下，刀具辅助坐标系坐标原点在分锥母线上的向量为:

根据式(5)，即可求得指形铣刀特征点在分锥面上的轨迹，如图3所示。面上的轨迹极坐标方程为:

3 加工起刀点坐标计算

加工仿真的机床模型如图4所示，轮坯和夹具安装于工件箱上，工件箱根据齿轮分锥角绕着和Y轴平行的轴线回转。加工齿轮时，轮坯和夹具绕着轮坯轴线回转的同时，刀具箱沿着X轴做进给运动，二者联动即可完成加工［2］。刀具箱还沿着Z轴可以做进给，完成进刀、退刀运动。

从机床正上方沿着机床坐标系的Y轴向下看，建立如图5所示坐标系，XOZ为机床的坐标系，是机床运动所依赖的坐标系，在没有刀具偏置、没有定义程序零点的情况下，刀具从其零点依照程序开始加工运动。

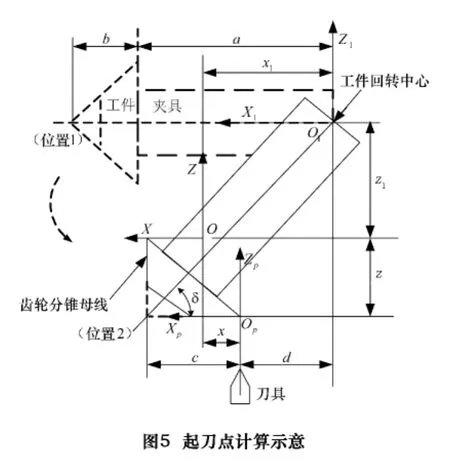
X1O1Z1为工件坐标系，它用于工件、夹具的安装，相对于机床零点有一个偏置量(x1，z1)。虚线所示的位置1是工件安装位，位置2是根据工件分锥角对工件回转后的位置。其回转中心为工件坐标系的坐标原点。

XpOpZp为程序坐标系，刀具加工的起刀位置即在程序坐标系的原点。它相对于机床零点有一个坐标偏置(x，z)，这个值就是要求的起刀点坐标。

图5中，a为夹具长度，mm;b为工件安装基面至分锥顶的距离，mm;c为分锥母线长度，mm;由图可得:d=(a+b)cosδ－c;x=x1－d;z+z1=(a+b)sinδ;z=(a+b)sinδ－z1。

4 凸凹面转换分度角计

冠轮平面［2］上指状铣刀与齿线的相对位置关系见图9，根据等基圆锥齿轮理论，当刀具沿着特定的运动轨迹运动时，刀具曲面包络出凸面或者凹面齿线。加工凹面时，在齿轮大端起刀处，冠轮平面上指状铣刀中心和理论齿线起点的夹角为θd1(图6)，对应于实际的轮坯加工中，指状铣刀中心和凹面齿线起点的夹角为e1(图7);加工凸面时，在齿轮大端起刀处，冠轮平面上指状铣刀中心和理论齿线起点的夹角为 θd2(图6)，对应于实际的轮坯加工中，指状铣刀中心和凸面齿线起点的夹角为e2(图7);

根据等基圆锥齿轮理论，θd1、θd2是理论齿线极径与刀具中心轨迹极径的夹角，

根据冠轮与轮坯的对滚关系［2］得:

实际加工中，刀具是沿着图6中的极径做直线移动的，轮坯按照特定的规律回转［1］。加工完毕一个凹面后，轮坯要进行分度，分度角度是图7中的θ角。加工完所有的凹面以后，轮坯要进行图7中的θx角度的回转，进行第一个凸面的加工，在下一个凸面的加工中，分度角度依然是图7中的θ角。分度角θ=360°/z，其中z是齿轮的齿数。图 7 中，θ1= θ2= θ/2，所以不难求得 θx角度，θx=θ1－e1－e2。

5 建立刀具模型

5.1 刀具截形的求解

指形铣刀轴截形切削刃部分应按其当量直齿圆柱齿轮的齿廓设计［1］。如图8所示，刀具轴截形坐标系σa(oa－ia，ja)的原点为当量齿轮的中心，刀具中线为齿间对称线;刀具辅助坐标系σn(on－in，jn)的原点为刀具轴线与当量齿轮分度圆的交点。

图8中，AB为圆弧，CD为设计刀具处当量齿轮齿廓渐开线，BC为连接AB与CD间的直线。轮齿齿廓修形由刀具廓线修形来实现，刀具廓线采用抛物线修形，修形中心点选择在当量齿轮分度圆上，修形量在圆周方向上度量，且仅对E点以上的部分修形，修形刀具廓线为ABCED'，半径rk处的修形量sk［3］为:

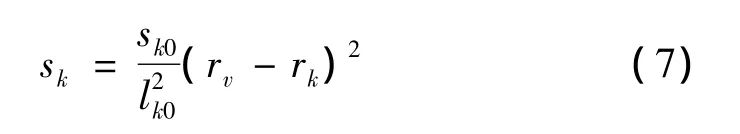
式中:lk0为齿廓修形参考点到修形中心点的距离，mm;sk0为lk0处齿廓修形量，由啮合分析确定，mm;rv为当量齿轮分度圆半径，mm。加工锥齿轮齿廓工作部分的刀具廓线CD段在坐标系σa下的方程为:

5.2 VERICUT模型的建立

依据式(8)，通过编程计算，可以获得一系列坐标值。打开VERICUT的Tool Manager界面，在图9所示的左方输入相关点的坐标，其坐标原点在图9中右边所示的O1点。

实际加工中，Z向进刀时，O1点须进给到程序坐标系的原点，以保证和等基圆锥齿轮的加工原理相符。但在VERICUT中，刀具安装的基点在图9中的O点，所以O点进给到程序坐标系的原点，因此在定义程序坐标系时，刀具Z向偏置距离Z1即可。生成的刀具安装在刀柄上后如图10所示。

6 数控仿真加工

6.1 加工程序

在加工程序的设计中，凸面加工使用一个子程序，凹面加工使用一个子程序，中间齿槽部分使用一个子程序，通过主程序调用子程序循环即可。具体程序的主体设计如下:

6.2 仿真结果

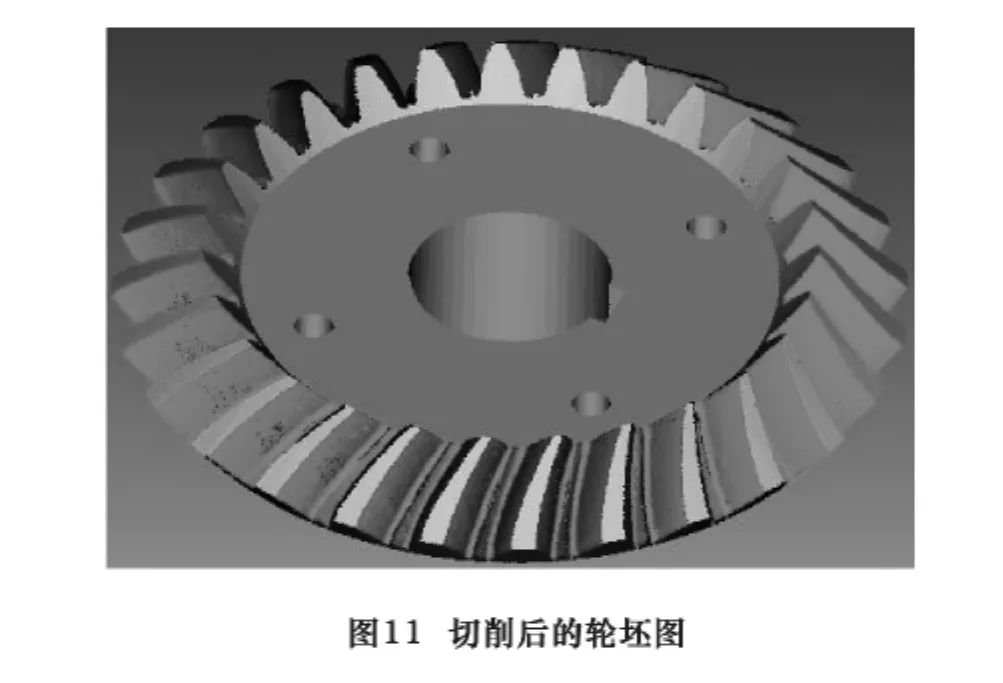
图11是轮坯只经过凹面、凸面切削后的状态图，对齿槽中间需要进行的第三刀辅助加工显然就容易实现了。将计算所得的理论齿面点导入三维软件，建立精确的齿轮三维模型，然后另存为stl文件后导入VERICUT软件，将仿真加工所得的齿面和该理论齿面进行比较，图12是比较的结果图。过切与欠切检测精度设为0.03 mm，图中除过切、欠切区域，其余部分齿面误差小于0.03 mm。

由图可知，指形铣刀加工的轮齿凹面小端有过切，大端有少量欠切;加工的凸面大端有少量过切，其余部分和理论齿面重合。齿槽底面显示欠切是因为只仿真加工了轮齿侧面，齿槽底面未精加工的原因。分析比较结果说明，所加工的齿面和理论齿面基本一致，运动轨迹求解正确。

7 结语

根据等基圆锥齿轮理论，通过合理的刀具轨迹规划、起刀点坐标计算、凸凹面转换中轮坯的回转角度求解、刀具的设计、实现了等基圆锥齿轮的数控加工，验证了等基圆锥齿轮数控加工的正确性及可行性，也为等基圆锥齿轮的数控加工提供了实例。

［1］蔡春源，程乃士.等基圆曲线齿锥齿轮原理.中国，91210712.X［P］.1990.

［2］巩云鹏.等基圆曲线齿锥齿轮传动原理、强度分析与跑合仿真研究［D］.沈阳:东北大学，1996.

［3］蔡春源，程乃士.等基圆曲线齿锥齿轮原理［J］.机械工程学报，1992，28(3):61 －64.

［4］巩云鹏，张伟华，蔡春源.等基圆锥齿轮的齿面啮合特性分析［J］.东北大学学报:自然科学版，1997，18(S):360 －364.

［5］张卫青，张明德，郭晓东，等.全数控锥齿轮铣齿机运动控制方法及切齿实验研究［J］.中国机械工程，2009，20(22):2733 －2737.

［6］唐进元，蒲太平，颜海燕.螺旋锥齿轮双重双面法多轴联动数控加工计算机仿真研究［J］.制造技术与机床，2008(2):25－29.

［7］韩佳颖，王太勇，李清，等.准双曲面齿轮切削仿真及齿面误差分析［J］.制造技术与机床，2010(1):112 －116.

［8］胡立志，赵家黎.圆弧齿轮指形刀具齿形计算研究［J］.制造技术与机床，2012(5):99－102.

［9］李铁军，朱成实.等基圆锥齿轮加工刀具轨迹的研究［J］.沈阳化工学院学报，2004(1):20－23.

［10］Gong Y P，Ding S C，Cai C Y.Analysis of tooth form error of equal base circle bevel gear［J］.Journal of Mechanical Engineering of China:English Edition，1996，18(1):52 －54.