舰船总体设计中的多学科优化技术
2013-09-27黄卫刚
周 奇,陈 立,许 辉,黄卫刚
(701研究所,武汉 320064)
0 引 言
20世纪80年代,多学科设计优化(MDO)兴起于航空航天领域。MDO是一种通过充分探索和利用工程系统中相互作用的协同机制来设计复杂产品及其子系统的方法论[1]。以Sobieski和Kroo为代表的科学家将其应用于飞行器结构设计中取得了良好的结果。目前,MDO广泛应用于飞机、运载火箭、汽车、涡轮引擎及潜器的设计[2]。
对于舰船总体设计领域而言,它涉及操纵、阻力、耐波、结构、声隐身、振动与噪声、工艺、材料等多个方面,是一个多目标、多变量、多约束的复杂工程设计问题。这些变量可能是离散、连续或非数值的;约束可能是线性或非线性的。就传统方法而言,船舶设计过程中对每个专业的分析是单独进行的,设计问题是以串行设计的方法来解决,其中每个学科有不同的优化问题,这种设计过程实质上是一种顺序求解,前面学科的结果往往决定后面学科的答案,而使设计陷入局部最优。
舰船是个复杂的巨系统,由很多子系统构成,各主要子系统之间均有强弱不同的耦合关系[3]。例如,改变舰船的结构设计将会改变舰船总重量,进而影响舰船的排水量、阻力及主机功率需求,同时也改变了舰船的质量分布,最终影响耐波性能、隐身性能;而改变舰船的阻力和推进特征又会影响所载燃料的重量,进而影响结构性能、空间利用情况及舰船的耐波性能。因此,为了获得整个系统的总体最优解,合理的做法是在设计期间同时考虑船型、结构、阻力等学科的设计,给出各学科的设计变量、约束条件以及各子系统之间的耦合关系,在满足系统总目标较优的情况下,设计各子系统,以获得各方面的综合平衡。多学科设计优化为舰船系统设计提供了一个有效的手段。国内将多学科优化应用于舰船总体设计的研究才刚刚起步,迄今为止还没有形成比较成熟的理论。
1 多目标协同优化
1.1 协同优化的思想
协同优化方法属于两级优化算法,将优化问题分为两级:一个系统级和并行的多个学科级(见图1),系统级向学科级分配系统级变量的目标值,各学科级在满足自身约束的条件下,其目标函数应使学科间耦合变量与分配的目标值的差距最小,经学科级优化后,各目标函数再传回给系统级,构成系统级的一致性约束,以解决各学科间耦合变量的不一致。通过系统级优化和子学科级优化之间的多次迭代,最终得到一个学科间耦合关系,达到一致的系统最优设计方案。协同优化算法的本质就是系统级协调优化算法。
1.2 协同优化的应用环境
协同优化方法在求解复杂的多学科问题时能体现出优越的特性,这些求解问题有如下共性[4]:
1) 需要进行大量子学科求解的复杂系统(集成优化和单级优化更适合简单问题);
2) 学科间耦合度低且系统级设计变量较少;
3) 学科级优化时需要利用特殊的优化算法,如轨迹设计时的离散优化,气动分析时的共轭优化;
4) 系统组织无严密的集成性。
应该注意,协同优化方法在求解时存在如下缺点:
1) 由于将状态变量看作设计变量扩大了设计变量的维数,耗费计算求解时间;
2) 系统级优化问题的表述形式导致系统级优化十分困难,当系统级耦合变量值处于可行域之外,要使系统级和子系统级耦合变量的不一致降低为0是非常困难的,这样要求更加完善的系统级优化算法;
3) 协同优化的收敛性目前仍未得到严格的证明,在实际应用中会遇到无法收敛或陷入局部最优的计算困难。
针对上述问题,许多学者从不同角度提出了一系列改进措施,包括一致性约束松弛、罚函数方法、引入响应面近似模型,系统层优化器中应用遗传算法、混合混沌算法等现代优化算法。
1.3 多目标协同优化
多目标协同优化的系统级优化问题表述为[5]:

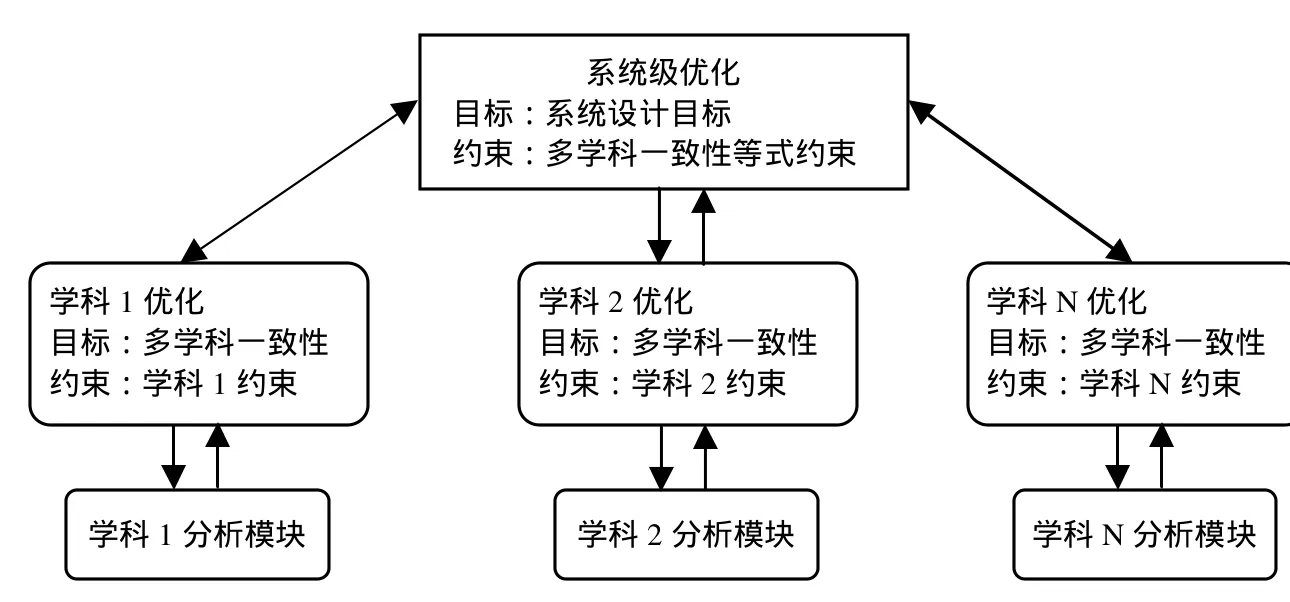
图1 协同优化框架
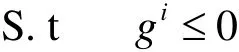
式中: Fi*——第i个学科的目标函数;x——交叉变量量 yij的辅助变量; gi≤ 0 ——局部约束条件。
由图 2可以看出各学科专家在处理其负责的学科任务时,只需要适时将计算结果存入数据库。并从数据库中提取所需信息后,就可完全按该学科获得最佳解的方向进行求解。系统层只要在消除各学科系统变量不一致性的基础上也就可能获得系统整体的最优解或满意解。求解基本步骤如下[6]:
1) 求出各学科的理想解,并构造系统层优化数学模型;
2) 系统层求解,获得辅助变量Z(系统变量)的初始协调值;
3) 在Z的初始协调值情况下,各学科引入相关变量的辅助变其一致性约束,并对其独立变量xi、系统变量x和辅助变行求解;
4) 得到各学科计算的有关信息之后,系统层再求解Z;
5) 系统层判断是否收敛,如收敛则结束,否则转到步骤6);
6) 得到Z的新的协调值之后,各学科将先前计算的各变量值作为初始值,再进行求解,然后转到步骤4);
7) 重复步骤3)~6)直至收敛。
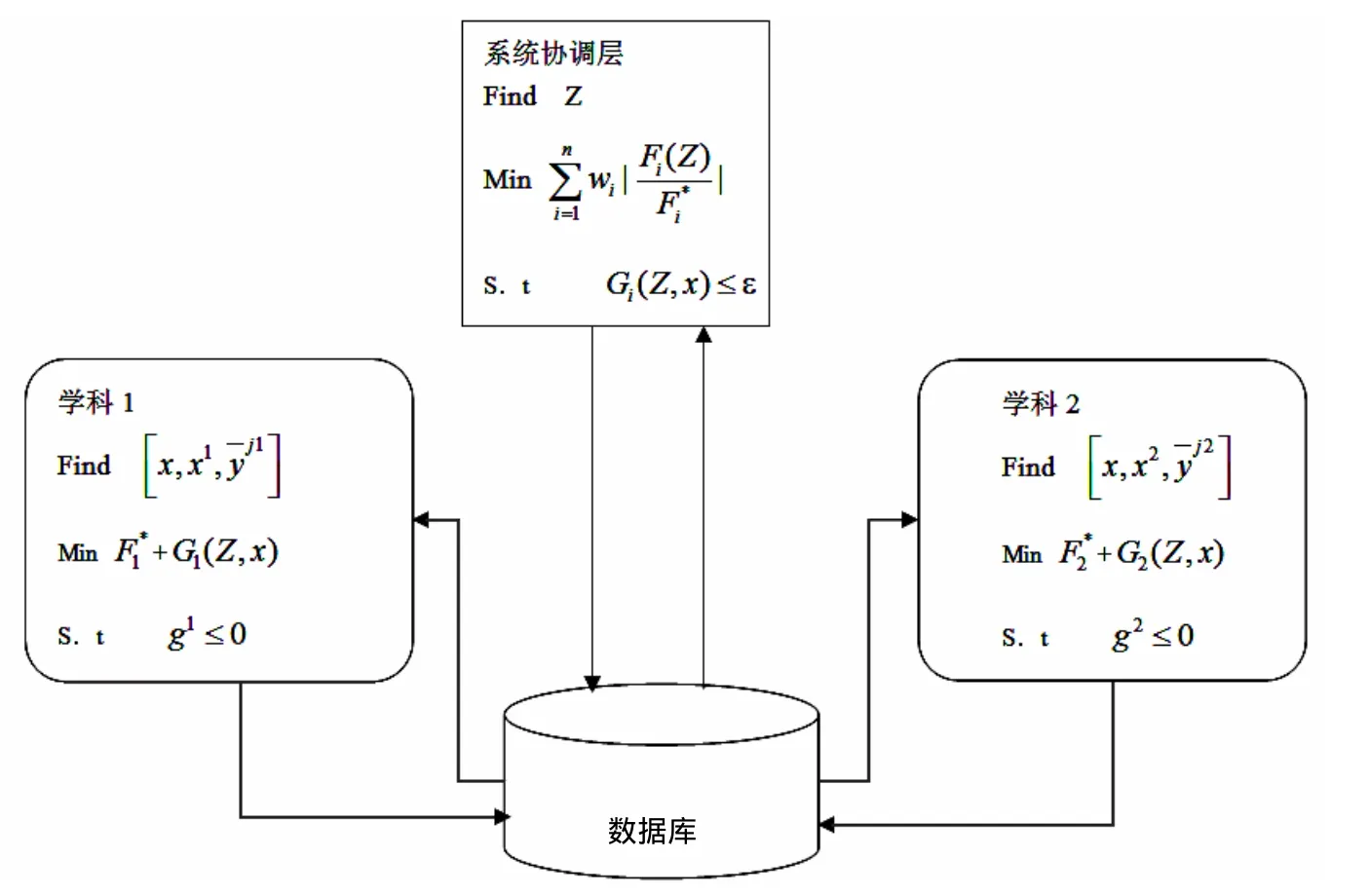
图2 多目标协同优化流程
2 舰船总体性能多学科优化
2.1 学科分析
舰船作为一个执行一定作战任务的复杂工程系统,进行舰船多学科优化的目的是要实现整个系统的综合性能整体最优,将舰船总体性能优化设计分为5个学科进行学科分析。
1) 浮态与稳性子系统:对于舰船设计而言,首先要保证舰船的浮态和初稳性,它取决于船型参数(船长、船宽、吃水,方形系数等);
2) 水动力性能子系统:水动力性能主要指快速性、耐波性、操纵性。其中快速性取决于舰船的阻力和推进性能,而阻力性能与船型参数、航速等有关。推进性能则与主机功率、转速、螺旋桨参数(螺距、桨径)、船型参数有关。耐波性与船型参数、航速、航向有关。操纵性与船型参数、螺旋桨参数、舵参数(舵角、舵高、舵宽)有关;
3) 造价子学科:舰船造价按照重量估算,并叠加相应的武备装置,与船型参数、主机功率、船用材料、武备单价数量等有关;
4) 隐身子学科:舰船隐身技术作为提升舰船系统生存、突防尤其是纵深打击能力的有效手段,与船型参数、船体布置,船用材料、螺旋桨参数等有关;
5) 振动与噪声子学科:舰船振动与噪声控制已成为舰船必不可少的战技指标,与螺旋桨参数、船体布置、船用材料等有关。
2.2 设计框架
舰船学科分析时,一般采用专业的软件进行学科分析,同时通过系统级协调共享参数。舰船总体设计优化框架如图3所示。
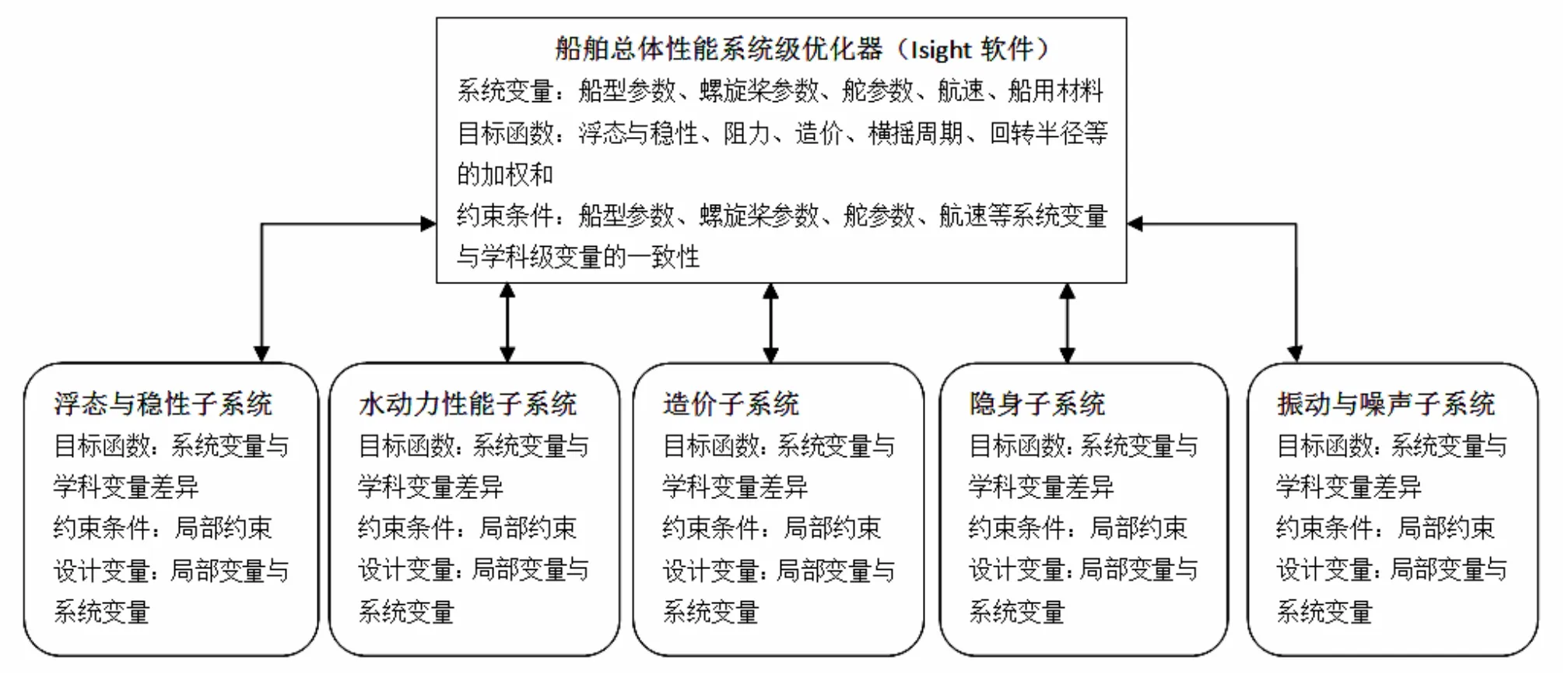
图3 舰船总体性能优化模型框架
2.3 计算环境
目前,在舰船研制领域的各学科相继引进了各类先进的设计分析工具,如结构学科的Ansys、Nastran、Patran等;快速性学科的Fluent、Shipflow等;耐波性学科的Hydrostar等;操纵性学科的Shipma、Napa等。这些设计分析工具的使用极大提高了设计效率和分析精度,可视化的多学科优化集成平台的建立使得这些彼此独立的设计分析工具不再局限于学科内部。
近年来,国外很多政府研究机构、大学和开发商积极地研发多学科优化软件框架,并取得较大的进展。现已在市场上占很大份额的集成框架有美国Engineous软件公司开发的Isight;Phoenix Integration公司的ModelCenter、Analysis Sever;TechnoSoft公司的AML等。其中Isight占市场份额的一半。
3 结 语
本文采用 MDO设计优化思路,利用多目标协同优化算法建立了舰船总体性能优化设计框架。MDO在航空领域应用广泛,这种将许多不同专业、约束、决策判据结合在一起的方法在舰船总体设计中的应用也会日趋广泛。
[1] Sobieszczanski-Sobieski J, Haftka R T. Multidisciplinary Aerospace Design Optimization: Survey of Recent Developments[J].Structural Optimization, 1997, 14(1): 1-23.
[2] Charles D.McAllister. Application of multidisciplinary design optimization to racecar design and analysis[A]. 9th AIAA/ISSMO Symposium on Multidisciplinary Analysis and Optimization[C]. Atlanta, Georgia: 2002.
[3] 刘祖源,冯佰威,詹成胜. 船体型线多学科设计优化[M]. 北京:国防工业出版社,2010.
[4] Kroo,I.M.Collaborative Optimization: Status and Directions[A]. 8th AIAA/NASA/ISSMO Symposium on Multidisciplinary Analysis and Optimization[C]. Long BeachCA: 2000. AIAA-2000-4721.
[5] Shu-yan Fu,Hai-yan Huang, Zhi-xiang Lin. Collaborative Optimization of container ship on static and dynamic responses[J].Procedia Engineering, 2010, 31: 613-621.
[6] 钟毅芳,陈柏鸿,王周宏. 多学科综合设计原理与方法[M]. 武汉:华中科技大学出版社,2006.
[7] A. DeMiguel, W.Murray. An analysis of collaborative optimization methods[A], 8th AIAA/NASA/ISSMO Symposium on Multidisciplinary Analysis and Optimization[C], Long Beach CA, 2000. AIAA-2000-4720.
