气候变暖下太湖极端洪水的归因探讨*

于 革 ，郭 娅 ，廖梦娜

(中国科学院南京地理与湖泊研究所，南京210008)

随着全球气温显著增加，人们观测到过去几十年的降水呈现明显的年代际变化［1］，而探究是否由人类活动排放温室气体导致全球增温并造成极端降水和洪水变化，是一个极具挑战的理论问题.近年来国内外一些探索性研究认为，北半球50年来最恶劣的暴雨和风雪事件呈上升趋势，年均升幅约为7%;而通过气候模拟研究，认为这些极端暴雨事件主要归因于温室气体作用下的全球增暖［2］.对2000年秋英国发生的特大洪水进行数值模拟，发现温室气体排放增加造成了温度升高、极端降水增强，引起特大地表洪水的发生由100年一遇加速到50年一遇［3］.这些研究揭示了增温引起降水和洪水的驱动机制并计算出所增加的份额，然而由于时间尺度局限在近50年，已经处于人类显著影响全球增温时段，这类研究还难以辨识增温中的自然系统下的脉动和变化份额.寻找现代全球增温下与工业革命前大气状况下的极端洪水事件，能够对比洪水强度和频率变化的差异，进而通过物理机制下的数值模拟能够获得对其差异的机制和归因认识［1-3］.

特大洪水属于极端水文事件.从统计上来讲，极端洪水事件是指洪水发生的频率或重现期严重偏离其平均态，在统计意义上属于不易发生的事件.根据现代水文观测数据，重现期超过50年的洪水被称为特大洪水［4］.对超过洪水50年一遇的小概率事件，常称为极端洪水［1，3］.长江下游太湖流域，历史和近现代不乏极端洪水发生［5］.新石器- 陶器时期太湖古文化的延续曾遭受数次大洪水侵袭而发生过中断［6］，洪水之患自古以来就是该区的最大威胁.20世纪发生了如1954、1992和1999年的特大洪水，其中由气象和水文仪器监测的1999年太湖流域洪水是自水文站监测以来的百年一遇的特大洪水［7］.根据历史文献记载，19世纪发生了如1823、1849和1889年的特大洪水［8-9］.有研究表明，采用相同水位标准估计1889年洪水水位比1954年洪水水位高出6 cm［9］.太湖流域19世纪末和20世纪末不同气候背景下的极端洪水事件，为洪水归因研究提供了难得的参照系.

我国东部长江中下游平原地势平坦，属亚热带季风气候，自古以来只要中、上游降雨过量，下游平原就出现水患［4］.现代太湖流域尽管人类围垦、建坝、土地利用等在一定程度上造成湖泊水体容量减少，或下游排水不畅导致洪水量的相对增大，但降水的增减仍然是流域洪水最重要的水源量［7，10-11］.因此，无论现代还是历史，降水都是控制流域洪水最重要的因素.在这个立论下，本文针对1990s和1880s的极端洪水历史，设计了太湖流域两个洪水年模式，在IPCC诊断的温室气体变化的方案下，采用4个GCM气候模拟驱动流域水文模拟，分析不同气候背景下极端洪水发生频率的差异，并进行极端流量不确定性的阈值模拟和风险系数论证，从而检测不同气候驱动下的洪水归因.

1 数据和方法

1.1 区域资料和模拟实验设计

太湖平均水位面积2338 km2，流域面积36895 km2.考虑到太湖为通江湖泊以及旨在洪水的气候归因研究，本研究集中于太湖流域上游来水区，主要位于西部山丘区和北部沿江区，模拟面积19055 km2.流域地形、水系、植被、土壤等自然地理资料来自于多年积累的流域基础数据库［12］.流域气象数据源于国家气象台站观测资料，包括流域内气象站1954----2009年逐日平均降水、最高与最低气温、相对湿度和风速.太阳辐射要素由最高、最低气温资料推算.作为率定模型参数和验证控制实验的水文资料，采用太湖大浦站1922-2009 年实测水位资料［11，13］、流域内河道巡测断面1988----2002 年流量［12-13］和太湖特大洪水资料［7，14］.

太湖是一个大型浅水湖泊，流域大部分的平原地势平坦，河床比降小，流速缓，流域输入太湖的输沙量在30～40万吨级;而由于太湖流域雨量丰沛，年降水量1100～1400 mm，入湖年径流量在40×108m3以上［15］，因此，太湖洪水变化主要受流域径流输入控制.本文采用分布式流域水文模型SWAT 2005［16］.对以湖泊水位和湖面高度变化为表征的产流、汇流的模拟研究已表明，SWAT能够胜任该流域的水文模拟［12］.对长期气候水文过程变化，笔者对过去200年以来的模拟研究，也表明SWAT能够模拟流域水量长期的年内和年际变化［17］.因此，围绕洪水的气候归因研究目标，笔者设计了采用该流域水文模型的模拟实验:

1)控制实验:太湖流域地形、水文、气候、植被、土壤等现代条件下的水文模拟实验，测试流域水文模型对太湖洪水的模拟能力;2)实验1:1990s极端洪水模拟，采用GCM气候模式驱动模拟15年(1988----2002年)，包括1999年特大洪水年的模拟;3)实验2:1980s极端洪水模拟，采用GCM气候模式驱动模拟15年(1880----1894年)，包括1889年特大洪水年的模拟.

控制实验是本项研究的基础，该实验的模拟过程和结果见文献［18］.对该模拟结果的检验［18］表明，在气候驱动下，该模型对现代或对历史的特大洪水具有较好的模拟能力，能够捕捉到小概率水文事件.因此，本文主要介绍实验1和实验2的工作，但采用控制实验的结果作为基线，检查实验1和2由GCM驱动的水文变化.模型SWAT在ArcView界面上运行，输出变量采用流域汇入太湖的逐日和逐月流量(Q)，并计算年平均流量、0.1% 和 0 .5%的极端洪水流量(Q0.1%和 Q0.5%).

1.2 极端洪水年的气候模式

根据《政府间气候变化专业委员会》第四次评估报告(IPCC-AR4)评估的过去150年来温室气体排放量方案(SRES)［1］，国际上多个气候模式组织采用SRES方案进行了全球大气环流模式(GCM)的气候模拟实验.目前在SRES方案下模拟过去150年以来的气候变化，有16个GCM被IPCC-AR4数据中心收录并发布［19］.根据应用经验［20-21］，本文选取了模式质量和精度相对较高、对东亚气候模拟相对适宜的海洋--生 物-冰圈与大气环流耦合的 G CM，包括了英国 H adCM［22］、德国 E CHAM［23］、美国 G FDL［24］和加拿大 C GCM［25］4 个模式.这4个 G CM的空间分辨率各异，HadCM3为格点模式，地表分辨率为2.75°纬度 × 3.75°经度;ECHAM5为谱模式T63结构，地表分辨率为1.875°纬度×1.875°经度;GFDL2为谱模式R30结构，地表分辨率为2.0°纬度 × 2.5°经度;CGCM3 为谱模式 T 47 结构，地表分辨率为3.75°纬度 × 3.75°经度.在 G CM 全 球输出中采用包含太湖流域在内的区域、地理位置围绕110°～120°E和28°～32°N范围的纬向和经向12个网格(3×4).

针对19世纪和20世纪不同气候归因下的洪水发生，本文采用IPPC-AR4两个方案下的气候模拟［1，19］驱动流域水文模拟:

1)20C3M方案:采用1850年以来观测到的大气温室气体增加状况进行气候模拟，代表了19 ---20世纪真实的大气温室气体变化，其中CO2浓度从工业革命前280 mg/L增加到2005年的379 mg/L，CH4浓度从715 μg/L增加到1774 μg/L.因此，该气候模拟从机理上反演20世纪温室气体实际增加下的气候变化.在此方案下，HadCM模拟了1850年以来140模式年，其他3个模式ECHAM、GFDL和CGCM分别采用1860、1861和1850年以来的150模式年.考虑到该方案下的模拟系温室气体150年来随着时间的实际增长变化，本文采用了1988 ---2002年15年气候模拟数据驱动实验1.

2)PICTL方案:采用工业革命前1850年大气温室气体作为常数对过去150年的气候模拟，代表了从机理上设置的20世纪温室气体未增加、工业革命前自然大气温室气体下的气候状况，其中CO2和CH4大气浓度分别采用280 mg/L和715 μg/L.HadCM、ECHAM、GFDL和CGCM在PICTL方案下分别模拟了自1859、1860、1860和1850年开始的340、505、500和500模式年.本文采用了围绕1889年前后的15年气候模拟数据驱动实验2.

1.3 不确定性分析

采用的GCM模拟的气候数据进行流域水文模拟，主要存在以下3方面的不确定性:

1)气候模式误差:包括不同GCM模拟实验对温室气体排放的大气层次、温室气体的光学物理和化学效应等不同设置、模式对大气环流和大气浓度不同系统的响应以及模式自身的系统误差.对此，本文采用4个GCM的多模式集合法［26］，以减少采用单个模式的误差.

2)全球空间尺度的GCM应用到太湖流域的区域误差:尽管根据应用经验选取了4个比较优秀的GCM，但这些欧美气候模式对东亚气候系统把握程度各异，应用到太湖流域可产生一定的不确定性［27-28］.因此，本文采用与观测资料序列拟合与校验的统计降尺度方法［29］，校正区域误差.

在逐日降水的随机模拟中，采用一阶马尔科夫链和和分布函数相结合证明可较好地模拟逐日降水过程［30-34］.本文应用该方法，首先用马尔科夫链描述降水日的发生，再用选定的分布函数拟合降水日的降水量，并采用实测数据予以验证.基本步骤如下:

i)首先根据1950----2000年太湖降水的实测数据，建立一阶马尔科夫链模型的两个基本状态(即降水日W和非降水日D)数据矩阵.然后，计算从2周内至年内的转移概率，即降水日到降水日转移概率P(WW)和非降水日到降水日转移概率P(WD)，使所分析的序列具有马尔科夫链的性质.

ii)选定的分布函数拟合降水日的降水量.由于本文研究极端值的变化，没有采用常用的Gamma分布函数［32-34］，而是采用了能较好描述极端值分布型的对数正态分布函数［30-31］.这个分布型经过了论证和检验适合太湖极端年份的降水分布［18］.由此估计出对数正态分布的位置参数(μ)和尺度参数(σ)，从而实现逐日降水的模拟.

iii)利用实测降水数据对极端年份(1999年)的逐日降水模拟进行了统计检验.结果表明，实测值与4个 GCM 模拟值的相关系数分别为 0.242(HadCM)、0.229(ECHAM)、0.202(GFDL)和 0.327(CGCM).在该极端年份的样本下(n=365)，总体相关系数检验P＜0.05，表明两个变量呈线性相关.

iv)该方法分别应用4个GCM在PICTL和20C3M方案下的逐月降水模拟，计算出太湖流域逐日降水序列.

3)有限样本认识极端值的误差:根据极端值理论，在认识极端水文事件的总体分布不完全的情况下，分析流量极端值存在着很大的不确定性.采用以下步骤进行随机统计模拟和不确定性阈值限定:

i)由于流量分布呈近似不对称型，可采用与降水相似、接近对数正态分布［31］的拟合.可利用流量序列分布的位置参数(μ)和尺度参数(σ)验证是否服从对数正态分布～Log-Normal(μ，σ)，并采用Kolmogorov-Smirnov 单样品序列检验(KS-test1)［35］;

ii)采用蒙特卡罗方法［3，28］对有限的15年样本序列按照正态对数分布进行大样本模拟;

iii)采用Bootstrap方法［36］对有限的15年样本序列进行置信区间模拟，从而限定其不确定性的统计范畴;

iv)根据论证的洪水偏态分布，采用Kolmogorov-Smirnov双样品序列检验(KS-test2)［35］对不同模式的结果进行差异性统计检验.

1.4 极端洪水的气候效应和风险系数

为了诊断温室气体变化下气候模式对洪水的影响，构建一个风险系数F值［37-38］用来定量描述太湖流域洪水在20世纪末与19世纪末的气候效应，并估测工业革命前气候与20世纪末气候所产生洪水风险的差异.F值采用PICTL方案下模拟的流量(QPICTL)与20C3M方案下模拟的流量(Q20C3M)之比:

F值无量纲，当F值＜0时，表示20世纪末的洪水风险减少，从0减少到最小值;当F值＞0时，表示20世纪末的洪水风险增加，从0增加到最大值.为了避免F值中分母为0，在QPICTL和Q20C3M15年的时间序列(n=5830 d)中，对流量标准化:

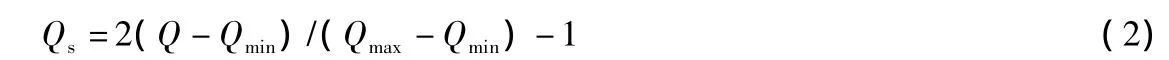
式中，Qs和Q分别是标准化后和标准化前的流量，Qmin和Qmax分别是标准化前最小和最大流量.这样，计算F值在(－∞，1)之间.尽管这个数据序列是一个不对称分布，可以通过计算风险系数在总体分布中(－∞，1)的百分位(%)［3］，以查看洪水风险的相对增减变化.

上述1.3和1.4节的数据矩阵和模式程序均在Matlab界面上处理、运行和计算.

2 模拟结果

2.1 现代气候模式的洪水模拟(实验1)

在实验1中，采用IPCC-20C3M方案的大气温室气体水平气候背景下4个GCM对1988----2002年气候模拟驱动，模拟太湖流域汇流过程，获得流域汇入太湖的逐日流量.在模拟的15年中，HadCM、ECHAM、GFDL、CGCM 的 平均流量分别为 1 82.1、181.6、167.8、171.9 m3/s.与 1 990s观测到的平均流量(183 m3/s)和控制实验平均流量(185 m3/s)相比，这些模拟比较接近观测值.由HadCM、ECHAM、GFDL、CGCM 4个GCM驱动，均模拟出1999年的极端洪水，其降水过程和模拟的洪水过程见图1.

对1988 ---2002年气候驱动的水文模拟计算0.1%的洪水流量，4个GCM模拟范围为2930～3603 m3/s，0.5%的洪水流量模拟范围为1843～1894 m3/s(图2a).根据日最大流量瞬时实测的记录，1983年7月3日是2770 m3/s，1991年6月5日是2450 m3/s，1999年6月28日是3029 m3/s［7］.实验1模拟的多年最大值达到其上限，认为可信.与控制实验模拟的小于5%洪水流量(Qextreme)相比，HadCM、ECHAM、GFDL、CGCM的均方根误差分别为 1 82、191、186、262 m3/s，相对误差分别为 7 .8%、10.3%、8.5%、8.1%，均在 1 0.3% 以 下，属经验可接受范围.此外，Bootstrap置信区间模拟，在P＜0.05水平上1990s流量均在控制实验的误差区域之内(图2a).

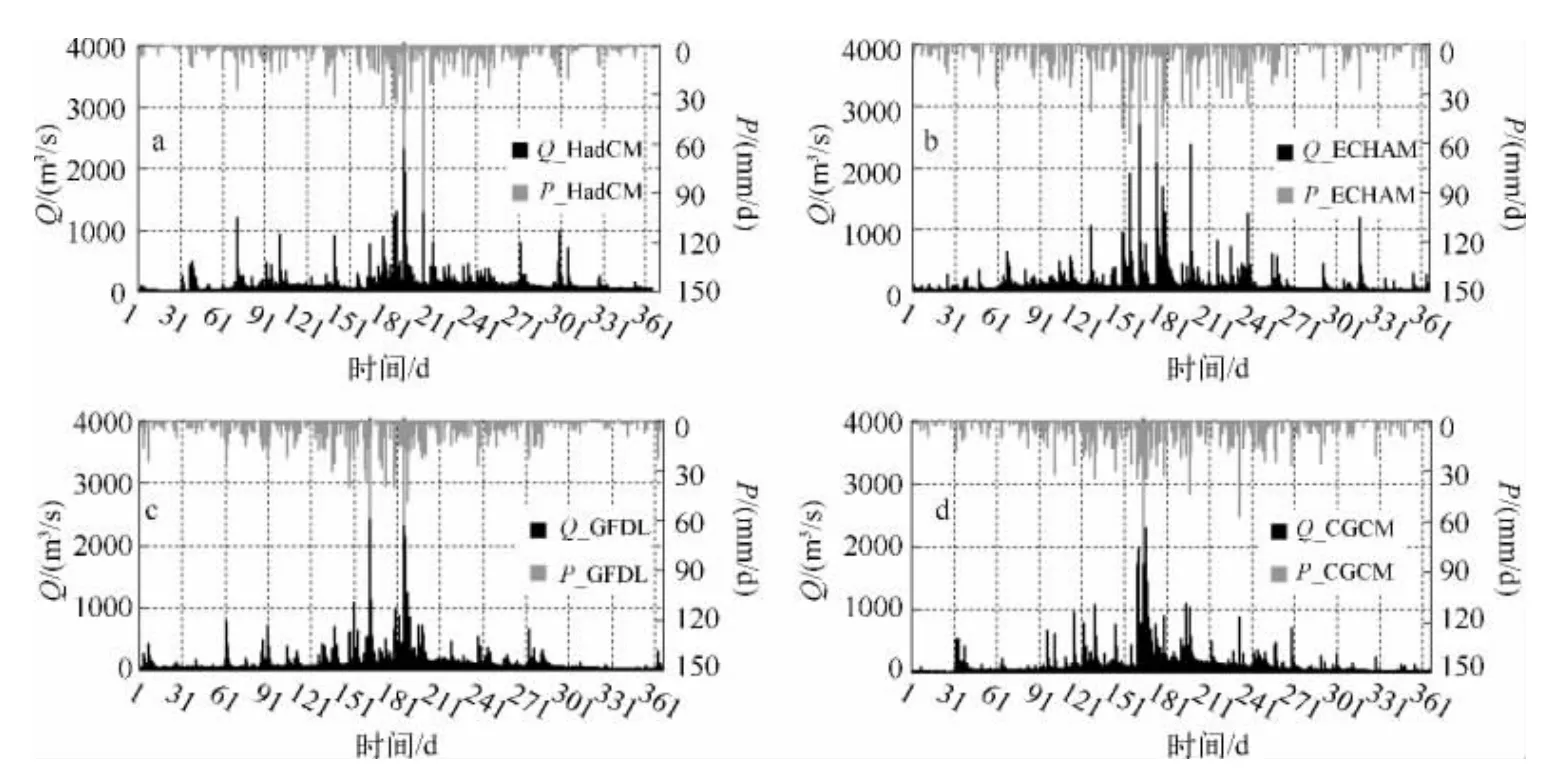
图1 4个GCM在IPCC-20C3M方案下1999年逐日降水(P)过程和所驱动的流域水文实验1的逐日流量(Q)过程Fig.1 Daily precipitation(P)simulations driving by four GCM simulations of IPCC-20C3M scenarios，and the driving 1999 daily discharge(Q)simulations in Exp.1

2.2 历史气候模式的洪水模拟(实验2)

在实验2中，采用IPCC-PICTL方案的工业革命前大气温室气体水平气候背景下4个GCM对1880-1894年气候模拟，模拟太湖流域汇流过程，获得流域汇入太湖逐日流量(图3a、b、c、d).在模拟的15年中，HadCM、ECHAM、GFDL、CGCM 的 平均值分别为 1 75.8、165.7、149.1、171.8 m3/s.模拟的流量逐日变化分布与各自GCM模拟的降水分布基本一致(图3e、f、g、h).

为了分析洪水极端值变化，画出在4个GCM驱动的15年流域水文序列模拟中≤5%的逐日洪水流量频率分布图(图2b).HadCM、ECHAM、GFDL、CGCM 驱 动模拟的0.1%的洪水流量范围为2069～3119 m3/s，0.5%的洪水流量范围为1437～1561 m3/s.与控制实验相比，可以观查到4个GCM气候驱动的极端流量(Qextreme)为0.01% ～2.00%部分显著降低.Bootstrap置信区间模拟的P＜0.05范围显示，1880s流量已经在控制实验的误差区域之外，可直观看到与控制实验的显著差异.

3 分析和讨论

为了分析不同气候模式对极端洪水的影响，对IPCC-PICTL和IPCC-20C3M两个方案下GCM气候模拟驱动的流域水文模拟进行对比.对实验1(1988----2002年)和实验2(1880----1894年)模拟的逐日流域流量输出，KS-test2检验表明，4个GCM的每两对方案下流量序列均具有显著差异(P＜0.017).主要统计量(表1)表明，工业革命前大气温室气体状况下的平均流量(165～196 m3/s)比1990s(192～215 m3/s)偏小，标准偏差也偏小.从极端值来看，Q0.1%和 Q0.5%的流量(2069～3119 m3/s和1436～1561 m3/s)均比1990s(2929～3601 m3/s和1842～1893 m3/s)显著偏小.

为了对比工业革命前(PICTL方案)与20世纪末(20C3M方案)4个GCM气候驱动下的洪水响应的差异，笔者采用样本n=10000服从正态对数分布的蒙特卡罗随机抽样模拟，以检查洪水流量在大样本下的极端值(图4a、b、c、d)和分布特征(图4e、f、g、h).流量模拟的4个GCM的 P ICTL模式在极端值区间比20C3M模式显著偏小(图4)，反映出大气温室气体在工业革命前的气候状况下，太湖流域极端流量比20世纪末显著减少(KS-test2检验，P ＜ 0.01).

检查IPCC-PICTL方案和20C3M方案下4个GCM气候模拟驱动的太湖洪水的发生风险，采用了风险系数(F值)定量描述上述“偏小”特征.根据公式(1)和(2)计算4个GCM在PICTL方案和20C3M方案驱动洪水模拟的F值，做出F值频率分布图(图5)，可以看到HadCM、ECHAM、GFDL、CGCM这4个模式的最大频率分别为 2 3%(F=0.6)、14%(F=0.6)、12%(F=0.2)和 1 8%(F=0.6)，4 个 G CM 洪 水风险系数出现频率最大值都为正值，代表着洪水风险的增加.计算各个序列的中值(50%百分位)可以查看该组数据中小于和大于一半的数据位居何处，结果显示HadCM、ECHAM、GFDL、CGCM4个GCM气候驱动下的风险系数的中值分别为0.44、0.15、－0.09、0.28，表明除了 GFDL模拟的流量风险系数中值接近于 0外，其他3个模式风险系数的中值均处于正值0.15～0.44，反映了洪水风险的显著增加.由于计算F值界于［－50，1］中，呈不对称分布，可以通过计算风险系数在总体分布中［－50，1］的百分位［3］，查看风险的相对增减变化.结果显示，HadCM、ECHAM、GFDL、CGCM 4个模式驱动的频率最大的洪水风险分别是60%、40%、20%和40%(图5)，反映出20世纪末的洪水流量变化较19世纪的风险显著增加20% ～60%.

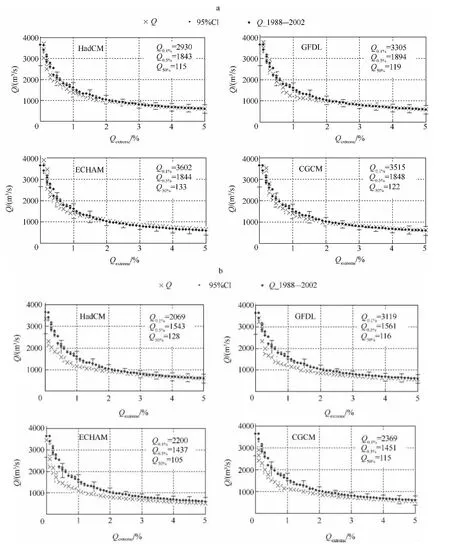
图2 4个GCM在IPCC-20C3M方案(a)和IPCC-PICTL方案(b)下驱动的流域水文模拟的逐日流量极端值频率(Qextreme＜5%)分布，并与控制实验的流量(Q_1988 ---2002)对比(蓝色误差范围为Bootstrap模拟的置信区间(P＜0.05))Fig.2 Frequencies of daily discharge extremes(Qextreme＜5%)by the hydrological simulations driving by four GCM simulations of IPCC-20C3M(a)and IPCC-PICTL(b)scenarios，and comparing with discharge simulations(Q_1988-2002)in the control run(Blue error bars are the Bootstrap confidence interval(P ＜ 0.05))

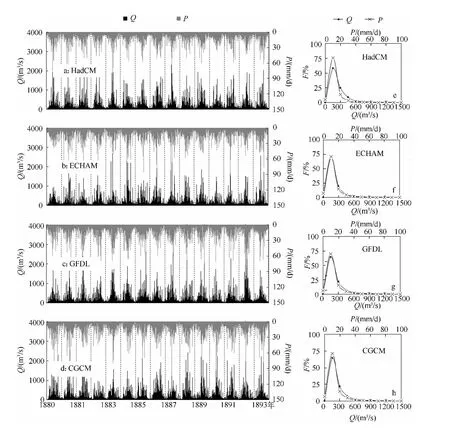
图3 4个GCM在IPCC-PICTL方案下逐日降水(P)过程模拟和流域水文实验2的15年逐日流量(Q)过程模拟(a、b、c、d)，以及相应降水和流量的频率分布(e、f、g、h)Fig.3 Daily precipitation(P)simulations driving by our GCM simulations of IPCC-PICTL scenarios and the discharge(Q)simulations in Exp.2(a，b，c and d).Frequencies of the precipitation(P)and discharge(Q)were plotted respectively in Figs.e，f，g and h

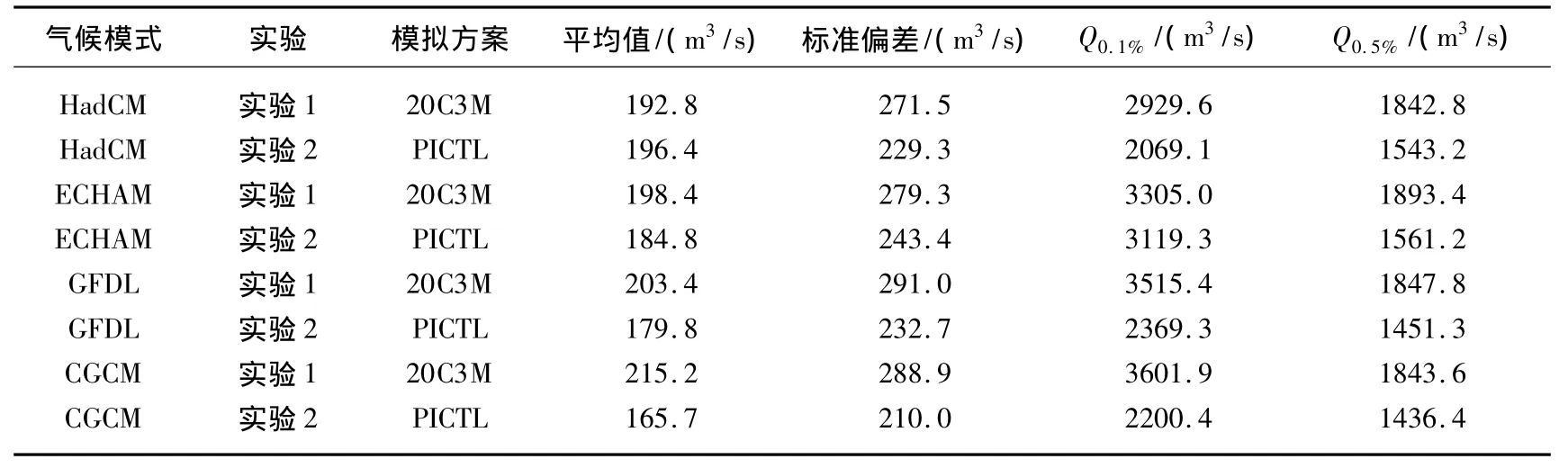
表1 实验1(1988----2002年)和实验2(1880----1894年)流域入湖流量模拟的主要统计量Tab.1 Major statistics of discharge simulations from Exp.1 and Exp.2

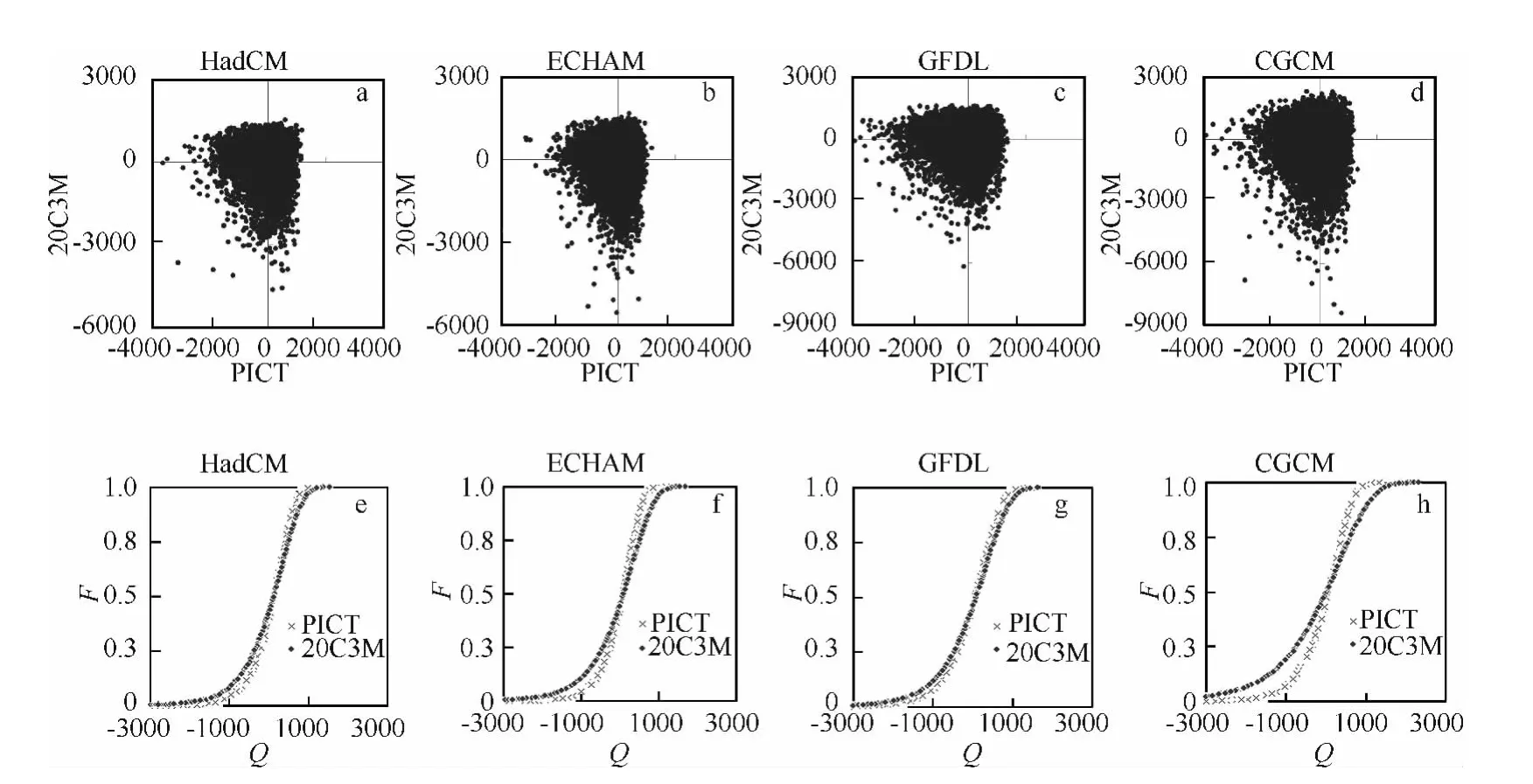
图4 蒙特卡罗模拟太湖流域不同时间逐日流量变化的频数变率分布(a、b、c、d:横坐标PICT代表19世纪末，纵坐标20C3M代表20世纪末)以及洪水风险系数(F)与频数变率(Q)的分布(e、f、g、h)，分别对比4个GCM工业革命前(PICTL方案)与20世纪末(20C3M方案)气候驱动下的洪水效应Fig.4 Frequency variability of daily discharge(a，b，c and d:the end of the 19th century in the horizontal axis and the end of the 20th century in the vertical axis)and flood risk ratio(F)vs.the frequency variability(Q)(e，f，g and h)by Monte Carlo simulations in the Lake Taihu catchment，comparing with flood effects of climate changes driving by four GCM simulations of the pre-industry time(PICTL scenario)and the 20th century(20C3M scenario)，respectively

4 讨论和结语

关于对全球增温是否能够引起降水增加超过气候统计意义上的变率、从而影响到极端洪水发生的认识，由于全球增温与气候系统脉动和振荡引起的温度变化互为交织，判识导致温室气体是否导致自然灾害加剧作用极为复杂，是灾害发生预测和对策研究中急需解决的瓶颈.此外，由于我国大部分观测资料时间开始于1950s，研究百年一遇以上的极端洪水受到时间长度的限制，存在着很大的不确定性.本文采用物理机制下的数值模拟与随机系统模拟结合对此进行了探讨，前者从气候驱动机制上模拟不同大气温室气候状况下的洪水结果，而后者旨在减少GCM驱动流域水文模拟过程中的不确定性.采用1980s包括1889年特征洪水年模式(农耕时代的流域系统下、自然的大气环流驱动模式)与1990s包括1999年特征洪水年模式(20世纪末流域系统下、全球增温下大气环流驱动模式)进行对比，能够较好地从机制认识洪水差异的归因，并能够进行极端流量的随机统计模拟和风险系数论证.

从模拟的洪水极端值来看，1990s流域极端洪水流量(Q0.1%为 2929 ～3601 m3/s，Q0.5%为 1842 ～1893 m3/s)比工业革命前大气温室气体状况下的洪水 流 量 (Q0.1%为 2069 ～ 3119 m3/s，Q0.5%为1436～1561 m3/s)显著偏大(KS-test2检验，P＜0.017)，4个GCM驱动的洪水产生的最大的风险在20% ～60%范围内，反映出20世纪末的洪水流量变化较19世纪的风险显著增加.

本研究中针对气候变化采用的驱动流域水文模拟，流域下垫面采用20世纪末的设置.因此，20%～60%的洪水增加风险估计包含了气候变化(降水、温度等)和流域下垫面变化(水利工程、土地利用等)两方面因素.尽管根据太湖流域研究［7，10-11］认为降水的增减是流域洪水最重要的控制因素，但下垫面变化的贡献仍然不可忽略.根据对1999年洪水灾害权重的研究，太湖围垦面积和泥沙淤积使湖泊容积减少5.2%，下游的淤塞使湖泊积水增加占24.3%～30.2%［39］.这两项均可以造成湖泊洪水水位抬升和相对湖泊洪水量(蓄洪量)增加.本文的太湖洪水效应来自于对入湖流量模拟，如果考虑湖泊洪水的蓄洪量中有30%～35%变化，则由于20世纪末气候降水变化的20%～60%洪水增加应该减去该项贡献，所以气候变化的洪水效应最大增量为25%.太湖流域1900s相对1880s下垫面变化从水文物理效应上的贡献，有待今后进一步研究，包括通过敏感性因子的模拟实验认识在总体增加风险中、人工改造下垫面因素的贡献份额.

大陆西岸的英国2000年秋季发生了百年一遇的极端洪水，经模拟研究认为由温室气体增加的气候变化引起的洪水风险增加了50%［3］.太湖流域人类活动改变的下垫面在1999年特大洪水中引起最大增量约35%［35］，本文模拟和分析的20世纪末气候下的洪水最大增量占60%，去除下垫面人为活动影响来估计洪水增加的最大增量在25%.因此，认为在我国东部长江下游、太湖平原地区，大气温室气体增加的气候变化可引发极端洪水发生的风险增加.这个认识有待进一步研究流域下垫面变化的水文物理效应，从而为认识与全球增温相关联的洪水灾害预测预警提供可靠的科学依据.

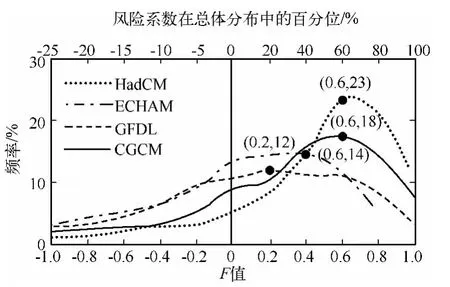
图5 PICTL方案和20C3M方案下4个GCM气候模拟驱动的太湖流量变化的风险系数(F值)分布和风险增减在总体分布中的百分位(%)(括号内数据表示最高频率的风险值和所占的频率)Fig.5 Frequencies of risk ratio(F-ratio)and the increasing percentiles(%)of the Lake Taihu extreme floods driving by four GCM simulations of PICTL and 20C3M scenarios

［1]I P CC.The fourth assessment report of the intergovernmental panel on climate change.Cambridge:Cambridge University Press，2007.

［2]M in SK，Zhang X，Zwiers FW et al.Human contribution to more-intense precipitation extremes.Nature，2011，470:378-381.

［3]P all P，Aina T，Dáithí A et al.Anthropogenic greenhouse gas contribution to flood risk in England and Wales in autumn.Nature，2011，470:382-385.

［4]中 华人民共和国水利部.水利水电工程等级划分及洪水标准.SL252----2000，2000.

［5]胡 明思，骆承政.中国历史大洪水(下卷).北京:中国书店出版社，1988.

［6]杨 怀仁，谢志仁，杨达源.全新世海面变化与太湖形成和演变.见:杨怀仁编.第四纪冰川与第四纪地质论文集.北京:地质出版社，1985:49-64.

［7]欧 炎伦，吴浩云.1999年太湖流域洪水.北京:中国水利水电出版社，2001.

［8]陈 家其.太湖流域历史洪水排队.人民长江，1992，32(2):30-33.

［9]《太湖水利史稿》编写组.太湖水利史稿.南京:河海大学出版社，1993:118-122.

［10]杨桂山，王德建.太湖流域——经济发展·水环境·水灾害.北京:科学出版社，2003.

［11]罗潋葱，秦伯强，朱广伟.太湖上游的水文特征及灾害分析.灾害学，2004，19(1):21-26.

［12]赖格英，于 革，桂 峰.太湖流域营养物质输移模拟评估的初步研究.中国科学:D辑:地球科学，2005，35(增刊2):121-130.

［13]中央水利部.长江流域水文资料·太湖区.南京:中央水利部南京水利实验处，1951.

［14]毛 锐.建国以来太湖流域三次大洪水的比较及对今后治理洪涝的意见.湖泊科学，2000，12(1):12-18.

［15]黄漪平，范成新，濮培民等.太湖水环境及其污染控制.北京:科学出版社，2001.

［16]Di Luzio，Srinivasa MR，Arnold JG.A GIS-coupled hydrological model system for the Watershed assessment of agricultural nonpoint and point sources of pollution.Transactions in GIS，2004，8:113-136.

［17]于 革，桂 峰.太湖流域营养盐沉积200年的历史模拟研究.沉积学报，2006，24(6):849-856.

［18]于 革，桂 峰，李永飞.太湖1899洪水年的流域水文模拟.湖泊科学，2012，24(6):651-657.

［19]IPCC Data Distribution Center.AR4 GCM data(Crown copyright 2005，Data provided by the Met Office Hadley Centre).http://www.ipcc-data.org，2008.

［20]Yu G，Shen H，Liu J.Impacts of climate change on historical locust outbreaks in China.Journal of Geophysical Research-Atmospheres，2009，114:D18104 1-11.

［21]Yu G，Shen H.Lake water changes in response to climate change in northern China:Simulations and uncertainty analysis.Quaternary International，2010，212:44-56.

［22]Johns TC，Gregory JM，Ingram WJ et al.Anthropogenic climate change for 1860 to 2100 simulated with the HadCM3 model under updated emissions scenarios.Climate Dynamics，2003，20:583-612.

［23]Roeckner E，Brokopf R，Esch M et al.Sensitivity of simulated climate to horizontal and vertical resolution in the ECHAM5 atmosphere model.Journal of Climate，2006，19:3771-3791.

［24]Manabe S，Stouffer RJ.Century-scale effects of increased atmospheric CO2on the ocean-atmosphere system.Nature，1993，364(6434):215-218.

［25]Flato GM，Boer GJ，Lee WG et al.The Canadian centre for climate modeling and analysis global coupled model and its Climate.Climate Dynamics，2000，16:451-467.

［26]Semenov MA，Stratonovitch P.Use of multi-model ensembles from global climate models for assessment of climate change impacts.Climate Research，2010，41:1-14.

［27]Moss R，Schneider S.Uncertainties in the IPCC TAR:Recommendations to lead authors for more consistent assessment and reporting.In:IPCC Supporting Material:Guidance Papers on Cross Cutting Issues in the Third Assessment Report of the IPCC.Geneva，2000:33-51.

［28]New M，Hulme M.Representing uncertainty in climate Change Scenarios:a Monte-Carlo approach.Integrate Assessment，2000，(1):203-213.

［29]Hewitson BC，Crane RG.Climate downscaling:techniques and application.Climate Research，1996，7:85-95.

［30]Hahn GJ，Shapiro SS.Statistical models in engineering.New York:John Wiley＆ Sons，Inc.，1967.

［31]Dingman SL.Physical hydrology:2nd edition.New Jersey:Prentice Hall，2002.

［32]廖要明，张 强，陈德亮.中国天气发生器的降水模拟.地理学报，2004，59(5):689-698.

［33]王 斌，付 强，王 敏等.几种模拟逐日降水的分布函数比较分析.数学的实践与认识，2011，41(9):128-133.

［34]杨文峰，陈德亮，胡春娟.天气发生器对陕西降水的模拟.陕西气象，2005，(5):5-7.

［35]Marsaglia G，Tsang WW，Wang J.Evaluating Kolmogorov's distribution.Journal of Statistical Software，2003，8:1-4.

［36]Efron B，Tibshirani RJ.An Introduction to the Bootstrap.Florida:Chapman ＆ Hall，1993.

［37]Allen MR.Liability for climate change.Nature，2003，421:891-892.

［38]Stone DA，Allen MR.The end-to-end attribution problem:from emissions to impacts.Climate Change，2005，71:303-318.

［39]秦伯强，胡维平，陈伟民等.太湖水环境演化过程与机理.北京:科学出版社，2004.