基于环网的短路电流计算方法研究
2013-09-25陶建鑫朱本坤
陶建鑫,朱本坤
(1.江苏科技大学 江苏 镇江 212003;2.镇江高专 江苏 镇江 212003)
目前,国内外常用的交流电力系统短路电流计算方法主要有国家标准(GB3321-82)、国家军用标准(GJB173-86)、IEC计算方法、图解法等等,而其中没有涉及到环形供电网络等复杂网络的短路电流计算[1]。
文中通过对国标法进行改进,利用电力网络简化先将发电机与其串联的阻抗进行等效,然后通过三角---星形变换将环网简化成简单的供电网络,再将等效后的发电机与其他发电机等效成一台发电机,最终直接与短路故障点通过阻抗相连的形式,通过发电机三相短路电流算法计算短路电流。
1 环形网络短路电流的等效计算
环形网络在发生短路故障时,发电机参数和电力网的结构对短路点的最大短路电流起决定作用,短路点距离电源越近,则系统的总阻抗就越小,短路电流值就越大。影响同步发电机的短路电流大小的参数主要有电抗类参数和时间类参数。电抗类参数的大小影响短路电流各分量的大小,时间类参数影响短路电流各分量的衰减速度。由于短路电流中超暂态短路电流分量的比例最大,衰减速度最快,所以超暂态短路电流分量的衰减速度对短路电流的影响最大[2]。
文中以简单二节点环形网络为基础,探讨环网短路电流的等效计算方法。假设4台发电机为同一型号,负载为静态负载,不贡献短路电流。
1.1 单台发电机馈送的短路电流
1.1.1 发电机对称短路电流
当发电机处在空载且额定电压的情况下,在发电机输出端发生三相短路时,超暂态对称短路电流初始值和暂态对称短路电流初始值分别为:
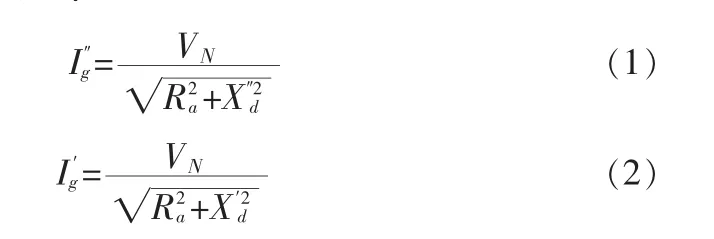
则短路发生后第一个半周时发电机馈送的对称短路电流为:

式中:
VN----发电机空载额定相电压;
Ra----发电机内阻;
Ia----发电机对称短路电流;
Td″----发电机直轴超暂态时间常数;
Td′----发电机直轴暂态时间常数;
T----为交流电周期;
Xd----发电机的稳态电抗;
Xd′----发电机的瞬变电抗;
Xd″----发电机超顺变电抗。
1.1.2 发电机短路电流非周期分量
当发电机处在空载且额定电压的情况下,其短路发生后第一个半周时短路电流非周期分量为:
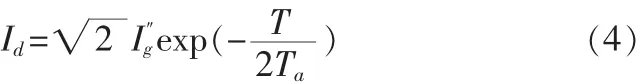
1.1.3 发电机最大非对称短路电流
发电机的非对称短路电流等于其对称短路电流的峰值与短路电流非周期分量之和[3],一般最大非对称短路电流发生在第一个半周时,当发电机在空载及额定电压下,输出端短路最大非对称短路电流为:

1.2 发电机串联阻抗(Rc+jXc)后等效发电机的参数
发电机机端串联阻抗对该发电机贡献的短路电流大小有很大的影响,为了将这部分的影响计算进去,需要将串联阻抗归算到原发电机中,二者等效为一台等效发电机,等效后的发电机电枢电阻Rd-e、直轴超瞬变电抗和瞬变电抗

发电机单机短路电流非周期分量衰减时间常数为:
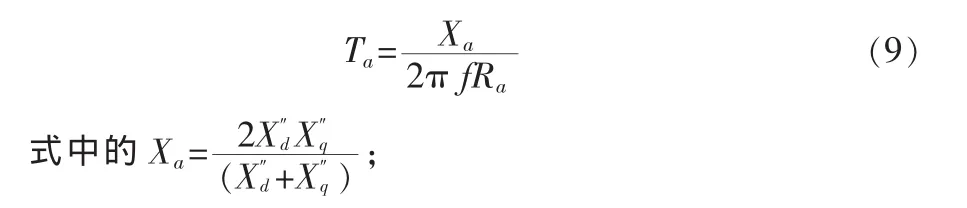
此时要用串联阻抗进行修正,等效发电机短路电流周期分量衰减时间常数为:

1.3 两台发电机并联后的等效发电机参数
两台不同规格发电机并联时,等效发电机的电枢电阻RA、超瞬变电抗、瞬变电抗、周期分量衰减时间常数非周期分量衰减时间常数TA分别为:

2 算例验证
2.1 环形供电网络的等效变换
首先做出环形供电网络的等值电路图,然后将电路图化简,如图1所示,以等效为基本原则,先将原发电机与串联阻抗等效为一台发电机,然后以等效后的发电机再与其他支路上的发电机进行并联,等效为一台发电机,层层化简后,最终将网络简化成一台发电机端三相短路的情况,则用单机机端短路的计算公式计算出总的短路电流峰值。

图1 等效电路化简过程示意图Fig.1 Equivalent circuit simplification process diagram
2.2 实例计算
计算以典型环形供电网络的短路形式为例,如图1所示,4台发电机分别向短路点馈送短路电流。
其中:
两配电板间线路阻抗为:4.28+j1.62 mΩ;
短路点左侧阻抗为:3.21+j1.215 mΩ;
短路点右侧阻抗为:1.07+j0.405 mΩ;
发电机至配电板间线路阻抗为:0.535+j0.202 mΩ。
发电机参数如表1所示,以环形供电网络的等效变换为参照,运用上述计算公式,一步步推导,最终得出短路电流计算结果:Ia=39.78 kA,Id=27.59 kA,Ip=83.85 kA。分别为原发电机参数与串联电阻或电抗的代数和。

表1 发电机参数Tab.1 Generator parameters
3 环形网络短路电流的MATLAB仿真
利用MATLAB的Simpowersystems工具箱对环形网络进行仿真,它的功能强大,不仅可以为用户提供了各种器件模块、组态平台、可选算法,而且输入输出方便,可以用于电路、电力电子系统、电机系统、电力传输等过程的仿真[5-6]。
环网模型如图2所示,其中仿真参数中选用的是变步长ode23tb(stiff/TR-BDF2),仿真时间为 0.35 s,系统以稳态为初始状态,短路器动作的时间为0.03 s,切断故障的时间为0.3 s,图3为F1点短路时短路支路的电流波形,短路电流峰值为82.10 kA。与计算值83.58 kA的误差控制在了3%左右,满足工程要求,达到了一定的精度,为系统选择电力设备提供了有效的依据。
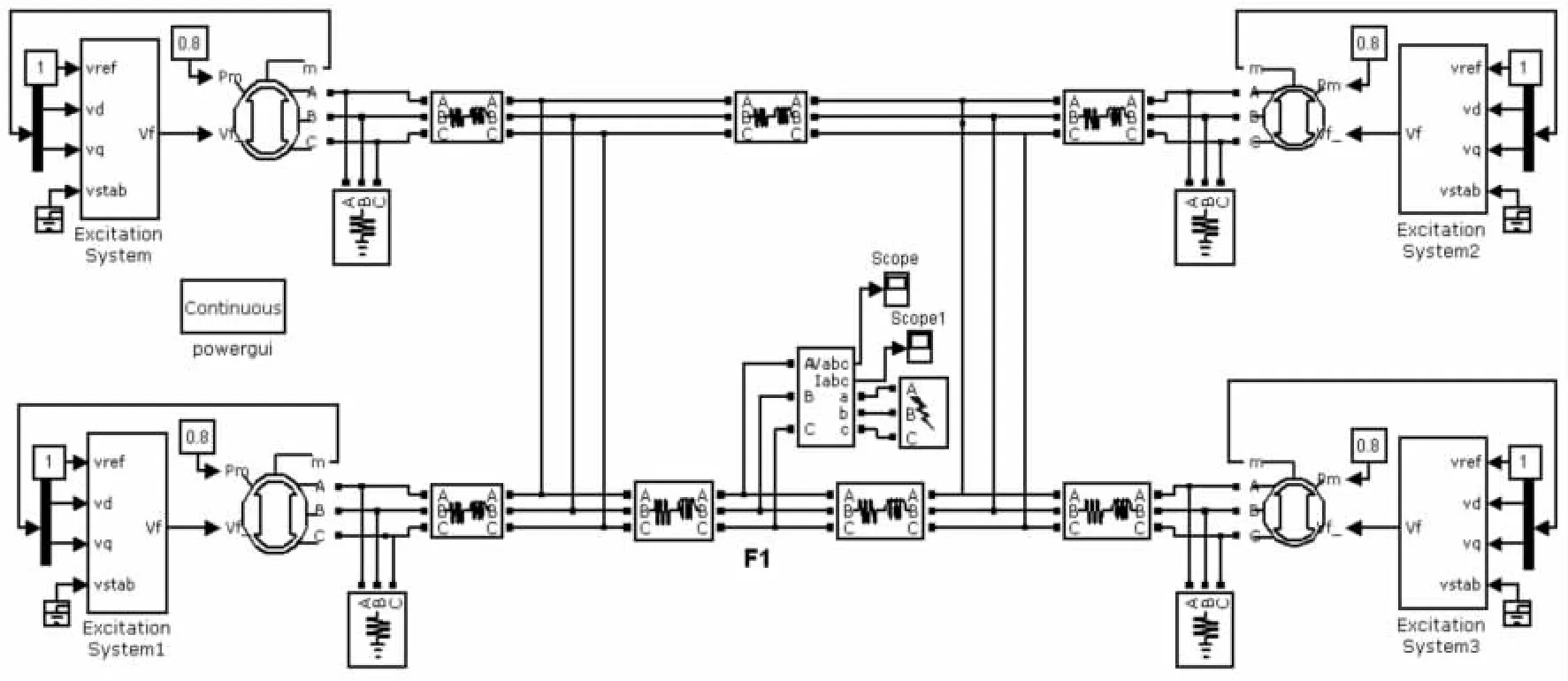
图2 仿真模型图Fig.2 Simulation model diagram

图3 F1点短路时短路支路的电流波形Fig.3 F1 points short circuit current waveform of the short-circuit branch
4 结 论
文中研究的是四机型环形供电网络的短路电流,通过对发电机与其串联阻抗的等效再与其他发电机进行并联,从而简化环形网络。经过多次仿真计算验证了这种方法的正确性和精度,对环形网络短路电流的计算进行了深入研究,为以后更加复杂的电力系统短路电流的研究奠定了基础。
[1]戴超,沈兵.船舶环形供电网络短路电流计算研究[J].船海工程,2006,175(6):97-99.
DAI Chao,SHEN Bing.Calculation of short-circuit current in marine loop power supply network[J].Ship and Ocean Engineering,2006,175(6):97-99.
[2]尚成枝,王德明,朱志宇.舰船环形区域配电结构及可靠性分析[J].船 电技术,2009,29(1):37-41.
SHANG Cheng-zhi,WANG De-ming,ZHU Zhi-yu.Structure of the marine looped zonal distribution and its reliability analysis[J].Ship power technology,2009,29(1):37-41.
[3]Electrical Installations of Ships and Mobile and Fixed Offshore Units—Part 1,Procedure for Calculating Short-Circuit Current in Three-Phase A C.IEC 61363-1.
[4]曹爽,唐石青,王骅.船舶环形供电网络的短路电流计算[J].船舶工程,2003,25(6):51-54.
CAO Shuang,TANG Shi-qing, WANG Hua.Calculation of short-circuit current in marine looped electric power system[J].Marine Engineering,2003,25(6):51-54.
[5]李维波.Matlab在电气工程中的应用[M].北京:中国电力出版社,2007:143-205.
[6]The MathWorks Inc.Power system blockset user’s guide[Z].Version 2.Natick, MA:The MathWorks Inc,2001.
