人工神经网络在金相图像分割中的应用研究
2013-09-25何维娜张丽丽
何维娜,张丽丽
(西安工业大学 计算机与工程学院,陕西 西安 710021)
人工神经网络在人工智能与模式识别领域应用非常广泛。由于其具有的高并行度,相当地分类速度和利用样本学习的能力,使其在涉及形状识别领域的应用更加广泛[1]。人工神经网络的最小单元是人工神经元,人工神经元是对实际神经系统中自然神经元的数学表征。材料科学是人工神经网络应用较为广泛地几个领域之一。例如,人工神经网络在焊接质量控制中的应用,在管道焊接中用于建立焊接参数,在钢材料中用于建立微结构与机械性能的复合模型,用于建立钛合金热成型应变模型,预测奥贝球墨铸铁性能,预测碳钢中碳含量和晶粒大小,用于获得陶瓷矩阵的组成单元,预测合金元素模型中的应力和显微组织演变,对金属显微图像中微结构进行分割和定量分析,钢在蠕变条件下工作时内部损坏地分类和实现球墨铸铁形态分析中的最佳图像二值化等[2-4]。人工神经网络也已非常适用于执行图像分割的任务。其实,许多必须基于人工神经网络的计算型视觉系统的开发主要是因为其具有的主要特点,如鲁棒性,执行速度和可行性地并行实施。
文中考察了模式识别领域常用地两种神经网络结构:基于BP算法(监督算法)的MLP结构和基于K算法(非监督算法)的SOM结构。这两种方法被用来对金相图像中的显微结构进行分割和对比。为了实际评价分割地效果,文中考察了球墨铸铁、可锻铸铁和灰铸铁的显微结构。选择这些材料的原因是由于其在工业领域的广泛应用,例如,机座结构,分层气瓶,阀门和泵的主体结构,齿轮元素等。
1 多层感知器神经网络
人类的大脑是由约10亿个神经元组成,脑组织的结构和功能复杂性高。所以,这些单元密集的内在联系形成了一个非常复杂的逻辑架构,至今仍是任何人工智能系统无法达到的。人工神经网络的出现是期望能够模拟人类大脑的潜能,特别是其学习能力[5]。第一个神经元数学模型是由McCulloch和Pitts[6]提出的。它有一个二进制输出端和几个输入端,每一个都带有不同的兴奋或抑制增益。这些增益被称为突触权重(或权重)。输入信号值和相关权重确定神经元的输出[5]。
因此,感知器或人工神经元是一个神经元细胞的数学模型,并且这些基本单元最终组成了人工神经网络。感知器架构包含一系列的输入(xi)n,每一个都包含相关的权向量(wi)和激活函数(fi)。可感知组织形成一个感知层,其中所有的感知器都链接相同的输入,但输出是不同的。这种网络被定义为感知器网络。只有被用来识别的图案是线性可分离的,单层感知网络才可以实现其良好的性能[5],因此,单层感知网络不能被用来解决复杂的分类问题,涉及非线性可分模式,通常用多层感知器网络来代替。
1.1 MLP架构
MLP是由一个输入层(Xi),一个或多个中间层或隐藏层和一个输出层(Y)构成。每一层都可以被定义成一个权向量矩阵(W)。这种人工神经网络的拓扑结构可以解决涉及非线性可分模式的分类问题并可以作为一个通用函数发生器[5]。
多层感知器网络包括训练和执行两个不同的阶段。在训练阶段,不能直接使用普通的三角规则[5],因为三角规则不允许重复计算隐藏层的权重。因此,MLP训练算法的最广泛算法是BP算法及其变种。这种学习方法比单层感知器网络更复杂[6]。
1.2 BP算法
标准的BP算法是训练神经网络最常用的算法[5]。该算法通过随机地初始化权值和将神经网络样本作为输入信号来实现的,这个信号通过隐藏层的传播处理实现输出层的输出。而权值则是通过下面方程来进行修正和调整:

式中,i是当前神经元的输入,j为神经元,l是当前层,s是神经元的输出,d为期望输出。最后,重复此过程直到误差小于之前设定的阈值。
该算法存在一些缺点,例如:1)易形成局部极小(属贪婪算法,局部最优)而得不到全局最优;2)训练次数多使得学习效率低下,收敛速度慢(需做大量运算)等。
1.3 MLP的拓扑结构
文中使用了两层结构的MLP。由于文中主要目的是从金相图中分割出材料的微结构,并将金相图像的像素分类为石墨结构,珍珠岩结构或铁氧体结构这些材料显微结构。因此,选择3/2/3(三路输入,两个隐层感知器和3个输出层感知器)的拓扑结构。对于每一个输入分配一个颜色组件(R,G和B),这些颜色组件对应被分割图像的一种像素类型。每个输出被分配给3种可能的像素分类:石墨结构,珍珠岩结构或铁氧体结构。隐藏层感知器数量的建立使用由YIN[7]等人提出的方法。最后进行显微定量,每一种分割后的显微结构所相关的像素被计数并且计算其在整体图像中所占的百分比。正如已经提到的,训练人工神经网络使用的是BP算法,而实验考察的是具有代表性输入图像的几类微观像素。应指出的是,一旦各种金属材料被分割出来之后,训练阶段就宣告完成。
2 SOM网络
自组织映射(Self-Organizing Maps,SOM)神经网络是由Kohonen[8]提出地包含在前反馈神经网络中使用非监督训练的一种拓扑结构。Kohonen的SOM神经网络在对外部信息输入形成拓扑映射结构的过程中,具有和人脑信息映射相类似的两个特点[9]:1)拓扑映射结构不是通过神经元的移动重新组织实现的,而是由各个神经元在不同兴奋状态下构成一个整体所形成的拓扑结构;2)这种拓扑映射结构的形成具有自织特点。因此,和反向传播网络(BP网络)等一类有监督学习的方法相比较,SOM神经网络算法更接近于人脑的认知过程。
SOM神经网络是一种前馈式无监督的学习网络,它由两层即输入层和输出层组成。其结构如图1所示。
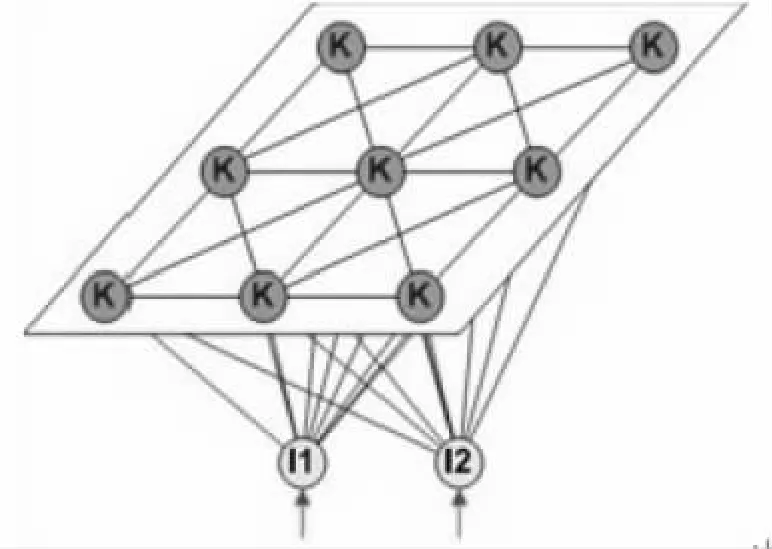
图1 SOM神经网络的结构Fig.1 Models of self-organizing Map Networks
图1中I1、I2为输入层神经元。输入层又称为匹配层,计算输入模式向量与权向量之间的距离,即匹配程度。输入层神经元的个数即为输入数据的维数。K为输出层神经元。输出层又称为竞争层,各神经元以匹配程度为依据进行竞争,确定匹配程度大(距离小)的神经元获胜。获胜的神经元及其邻域内的神经元权向量朝与模式向量更靠近的方向更新,其它神经元的权值向量保持不变。经过多次反复的这种竞争与更新,最终神经元就会学会模式向量,并以权向量的形式保存下来,这一过程就是自组织学习(映射)。可见SOM神经网络的学习映射包括两部分:最佳匹配神经元的选择和权向量的更新。
SOM神经网络中每一个神经元都代表一个输出。这个网络的拓扑结构的另一个特点是,其中的神经元是完全连接(突触连接)的。因此,如果有10个输入端,那么每个神经元也相应的有10个输入端,每一个神经元都与输入层有一个连接点。每个突触连接都对应一个权向量,如果网络中存在10个输入点,3个神经元,那么就应该有30连接(每一个神经元有10个)相应的就有30个突触权向量(每一个神经元有10个)。
2.1 近 邻
自组织映射网络中的神经元及其周围的神经元可以通过一定的拓扑关系而组织起来,从而使得它们能够对给定的刺激具有最佳的反馈。这种特性与人脑中神经元的活动是相似的,即以获胜神经元为圆心,对近邻的神经元表现出兴奋性侧反馈,而对远邻的神经元表现出抑制性侧反馈,近邻者相互激励,远邻者相互抑制。
2.2 神经元自适应
神经元自适应包括权向量调整,搜索对确定刺激的反应改善。实现权向量调整的第一步就是确定获胜神经元。而获胜神经元就是输入模式向量与权向量之间欧氏距离dt(n)最短的神经元,计算公式如下:
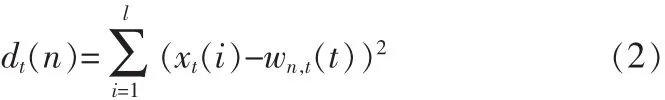
式中,xt(i)是时刻 t的第 i个输入向量,wn,t(i) 是神经元 n在时刻t的第i个权向量,i是I个输入端网络的输入向量和权向量的系数,dt(n)是神经元n在时刻t的欧氏距离。
事实上,最小欧式距离的神经元就是权向量值与输入向量值最接近的那个。如此以来,在每一次迭代中,获胜的神经元及其邻域内的神经元权向量朝与模式向量更靠近的方向更新,其他神经元的权值向量保持不变。权向量的调整在接下来的t+1时刻也是同样的适应过程。而临近神经元权向量的调整也是遵循同样的准则,如下所示:
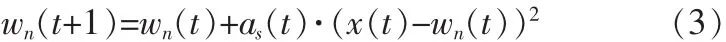
式中,0<as(t)<1 为学习速率,是一个增益函数,随时间而减小。
2.3 迭 代
迭代或世代的次数与被提取的输入模式的次数有关。每一个世代中,都必须提取所有的输入数据。而每一个输入模式都有一个获胜神经元被确定下来。接着,获胜神经元及其邻近神经元的权向量开始自我调整。当上一个输入模式被提取之后,一个新的世代就会开始并且所有的输入数据被再次提取。
2.4 SOM网络的训练算法
1)确定迭代的次数;
2)使用随机值对网络权向量进行初始化;
3)确定每个神经元的初始邻里半径(这是最初的邻里半径建议使用整个网络的初始半径);
4)给网络提供一个输入;
5)根据欧氏距离计算每个神经元的输出;
6)选择获胜神经元;
7)更新或者调整获胜神经元及其邻域内神经元权向量;
8)如果依旧存在近邻,就减小邻近半径;
9)如果仍然存在输入数据,返回步骤4;
10)增加世代数量,如果允许的最大世代数量仍未实现,返回步骤4并且再次提取所有输入数据;
非常重要的是,初始的权向量值必须是与每一个输入数据不同并且小于输入数据的;否则,就不会出现自组织的映射和竞争。
2.5 获胜神经元
训练结束之后,就可以根据输入模式的分类对每一个神经元进行标记。事实上有多个神经元会因为邻近神经元的原因而被归为同一对象。如果发生了这种现象,就需要对计算结果进行必要的后处理。
2.6 SOM网络的拓扑结构
文中所用到的SOM网络拓扑结构是1维的,并且其主要的任务是实现对金相图像材料显微结构的分割。SOM网络是被用来识别金相图像的像素颗粒属于石墨结构,珍珠岩结构或铁氧体结构中的某一种,因此,需要有3个神经元节点,并且每个神经元有3个输入的网络。而由于图像中每个像素的值包含R、G、B 3个分量,所以每一个输入点对应R、G、B中的一个分量,即输入数据的维数为3。而每一个神经元对应石墨结构,珍珠岩结构或铁氧体结构中的一类。为了实现定量分析,要对分割出来的各个像素进行计数和所占相对百分比的计算。用来训练网络的Kohonen训练算法。
3 结果和讨论
文中的目的是分割金相图像中的材料微观结构,因此,文中使用了两种人工神经网络结构来识别石墨结构,珍珠岩结构或铁氧体结构这3种微观结构。并且通过使用MLP和SOM对球墨铸铁、可锻铸铁和灰铸铁的分割应用获得了实验结果。
前面的章节介绍了MLP和SOM神经网络的结构,但是两种网络结构都只能用来把材料微观结构分成两类,一类代表石墨结构(输入图像中的黑色部分),另一类代表珍珠岩或铁氧体结构(输入图像中的灰色部分)。珍珠岩/铁氧体结构被归为一个类别是因为这两种结构在视觉上不能被有效地区分。
文中所用到的输入图像的像素是640×480;MLP所用的是BP算法,学习率是0.1,最大迭代次数为2 500,绝对误差<0.01;SOM在训练时所用的是Kohonen算法,学习率为0.1,最大迭代次数为2 500。
表1是使用MLP和SOM对球墨铸铁处理的结果。从表1中可以发现,两者处理的结果最大相差了5.7%(如样本7),最小相差了0.99%(如样本10);进一步计算可以发现MLP分割后,图像中石墨结构的平均含量是12.62%,珍珠岩/铁氧体结构的平均含量是87.28%;而SOM分割后的图像中这一含量分别为15.67%和84.23%;两种方法处理后的差异率平均值为3.05%。
图2是处理前后的球墨铸铁金相图,图2(a)是原始的球墨铸铁金相图,图 2(b)和(c)分别是 MLP和 SOM分割后得到的球墨铸铁金相图;综合图和表中的结果可以发现,MLP分割处理的结果比SOM分割处理的结果更加精确,因为SOM把部分珍珠岩/铁氧体结构错误地归类为石墨结构。
表2是使用MLP和SOM对灰铸铁处理的结果,从表2中可以发现,两者处理的结果最大相差了14.73%(如样本9),最小相差了1.83%(如样本7);进一步计算可以发现MLP分割后,图像中石墨结构的平均含量是12.71%,珍珠岩/铁氧体结构的平均含量是87.29%;而SOM分割后的图像中这一含量分别为21.79%和78.21%;两种方法处理后的差异率平均值为9.08%。
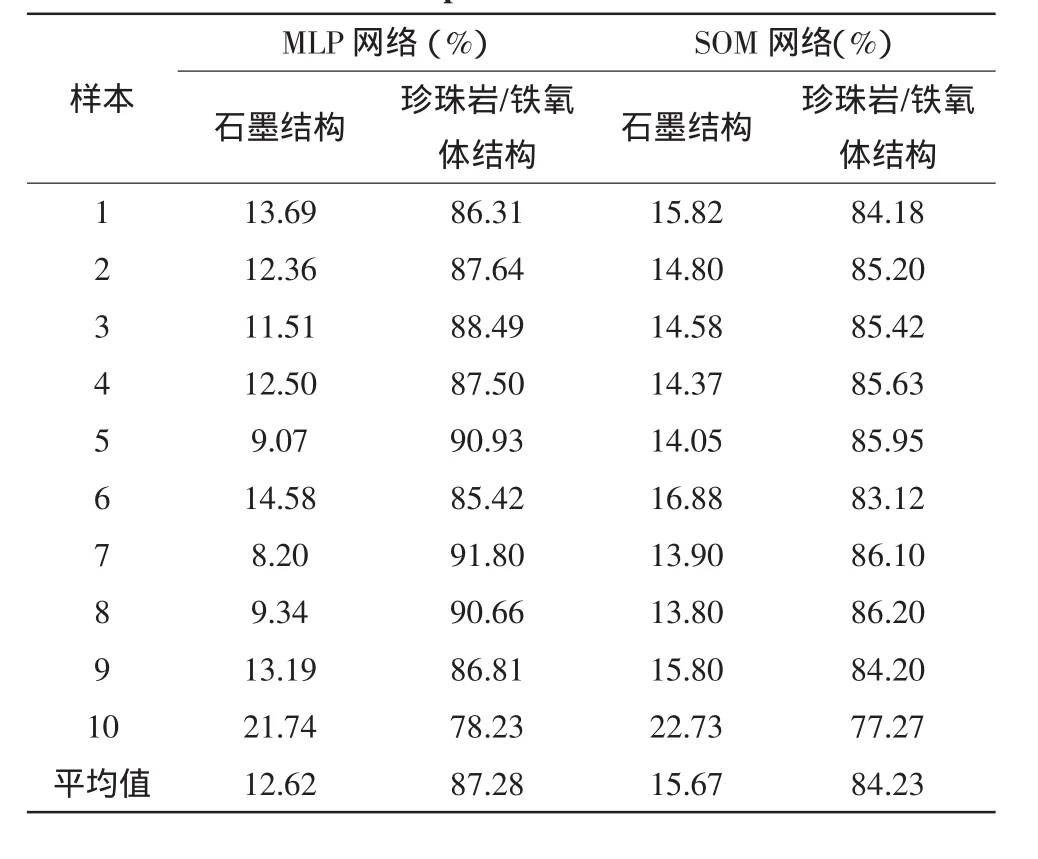
表1 MLP和SOM对球墨铸铁金相图分割的结果Tab.1 Results obtained using MLP and som based neural networks on samples of a nodular cast iron
图3是处理前后的灰铸铁金相图,图3(a)是原始的灰铸铁金相图,图 3(b)和(c)分别是 MLP和 SOM分割后得到的灰铸铁金相图。
综合图3和表2中的结果可以发现,MLP分割处理的结果比SOM分割处理的结果更加精确,这与对球墨铸铁分析的结果非常相近,同样是因为SOM把部分珍珠岩/铁氧体结构错误地归类为石墨结构。
表3是使用MLP和SOM对可锻铸铁处理的结果,从表3可以发现,两者处理的结果最大相差了5.69%(如样本6),最小相差了1.66%(如样本1);进一步计算可以发现MLP分割后,图像中石墨结构的平均含量是14.44%,珍珠岩/铁氧体结构的平均含量是85.56%;而SOM分割后的图像中这一含量分别为18.45%和81.55%;两种方法处理后的差异率平均值为2.89%。

图2 处理前后的球墨铸铁金相图Fig.2 Qriginal image of a nodular cast iron
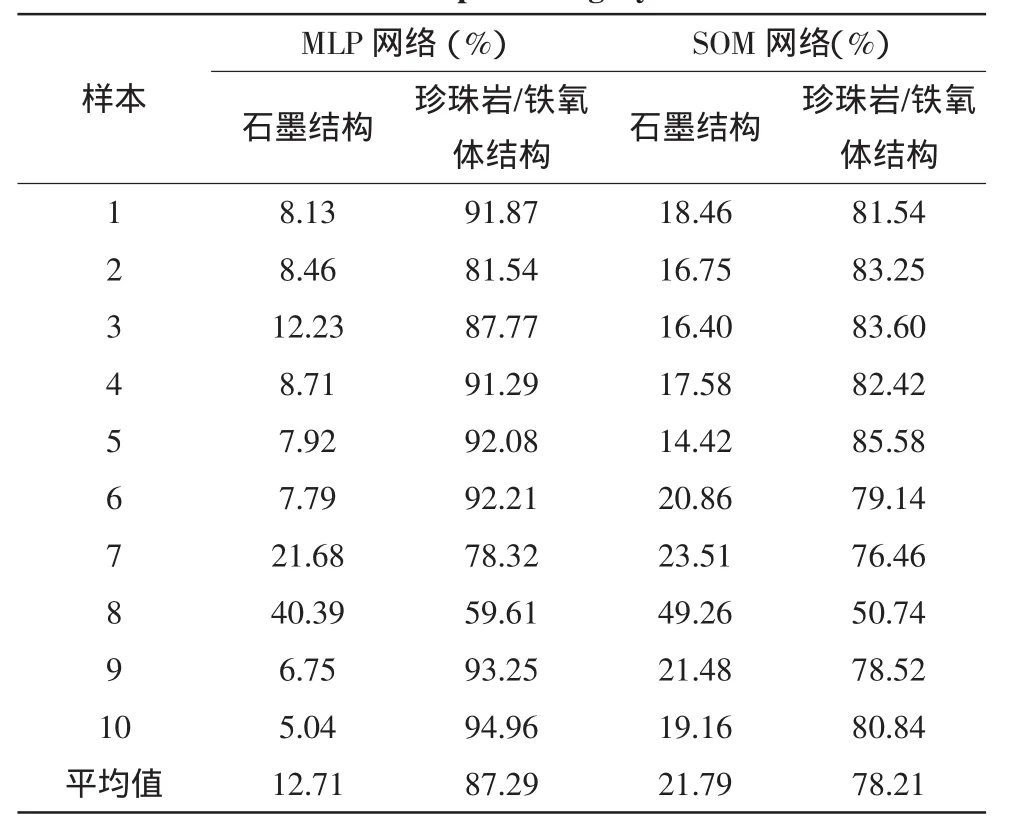
表2 MLP和SOM对灰铸铁金相图分割的结果Tab.2 Results obtained using MLP and SOM based neural networks on samples of a gray cast iron
图4是处理前后的可锻铸铁金相图,图(a)是原始的可锻铸铁金相图,图(b)和(c)分别是 MLP和SOM分割后得到的可锻铸铁金相图。
从上面的结果可以发现,利用MLP和SOM对样品1处理的结果非常相近,而对样品6处理的结果相差很大,从图4(c)可以发现,是因为SOM把大部分珍珠岩/铁氧体结构错误地归类为石墨结构,而MLP可以正确地将石墨结构分割出来造成的。
从MLP和SOM神经网络对球墨铸铁、灰铸铁和可锻铸铁金相图分割的结果来分析,可以发现当输入图像的背景不够均匀时会对成功分割石墨结构造成一定的困难;但是,MLP网络可以有效地将其分割提取出来。即使输入图像的质量较差,MLP网络仍然能自适应地和顺利地对金相图像显微结构实现有效地自动化分割。另外,相比SOM网络,MLP网络实现显微结构的分割所需的时间更短。
4 结 论

图3 处理前后的灰铸铁金相图Fig.3 Original image of a gray cast iron
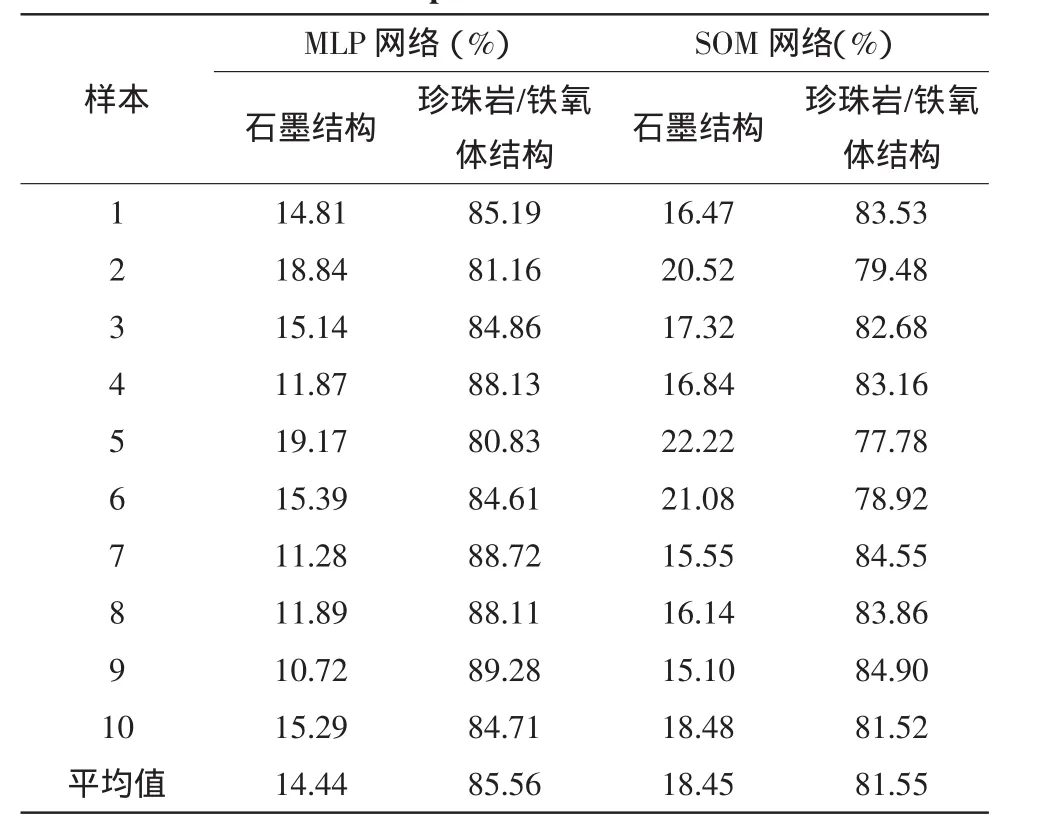
表3 MLP和SOM对可锻铸铁金相图分割的结果Tab.3 Results obtained using MLP and SOM based neural networks on samples of a malleahe cast iron

图4 处理前后的可锻铸铁金相图Fig.4 Original image of a malleable cast iron
文中利用MLP网络和SOM网络对金相图像中的微观结构进行了分割。其中MLP网络是基于BP算法的,而SOM网络则是基于Kohonen算法。在图像采集过程中,这两种方法相比传统的分割方法,例如阈值法,对噪声和无规律照明有更强的鲁棒性。对比分析使用MLP网络和SOM网络对球墨铸铁、灰铸铁和可锻铸铁金相图的分割结果可以发现使用MLP网络的分割效果更佳。据此,可以推断MLP网络能够成功地应用于材料科学领域,特别是用于对金相图像中微观结构的分割和处理。另外,相比SOM网络,MLP网络的主要优点是分割所用的时间更少和图像分割质量更佳。
[1]Samarasinghe S.Neural Networks for Applied Sciences and Engineering:From Fundamentals to Complex Pattern Recognition[M].Philadelphia, PA:Auerbach Publications,2006.
[2]Biernacki R,Koz "owski J,Myszka D,et al.Prediction of properties of austempered ductile iron assisted by artificial neural network[J].Materials Science,2006,12(1):11-5.
[3]Kim I,Jeong Y,Lee C,et al.Prediction of welding parameters for pipeline welding using an intelligent system[J].The International Journal of Advanced Manufacturing Technology,2003,22(9-10):713-719.
[4]Kusiak J,Kusiak R.Modelling ofmicrostructure and mechanical properties of steel using the artificial neural network[J].Journal of Materials Processing Technology,2002,127(1):115-121.
[5]Haykin S.Neural networks and learning machines[M].USA:Prentice Hall,2009.
[6]Mc Cullogh WS,Pitts W.A logical calculus of the ideas immanent in nervous activity[J].Neurocomputing,1988:15-27.
[7]Yin XC,Liu CP,Han Z.Feature combination using boosting[J].Pattern Recognition Letters,2005,26(16):2195-2205.
[8]Kohonen T.Self-organized formation of topologically correct feature maps[J].Biological Cybernetics,1982,43(1):59-69.
[9]李春艳.自组织映射(SOM)型神经网络的实现[J].电脑知识与应用:学术交流,2007,11(4):821-823,839.
LI Chun-yan.Reflect to shoot a realization of nerve networks from the orgamization[J].Computer Knowledge and Technology:Academic Exchange,2007,11(4):821-823,839.
