大地-电离层谐振腔中极低频电磁波传播的数值模拟
2013-09-25谭仕文
谭仕文
(92330部队 山东 青岛 266102)
极低频电磁波在地球物理勘探、地震预报等领域具有重要的用途。由于频率很低,波长很长,极低频电磁波的激励与传播可以看作是大地-电离层谐振腔中电磁场的空间分布问题[1]。这是一个典型的球面分层介质中的边值问题[2],分析方法有近似解析方法和数值方法。目前国外学者主要采用解析方法来求解该问题,而解析方法在具体的处理技巧上又有所不同。其中一种方法是利用波长远大于电离层高度的特殊条件,得到大地-电离层腔体中齐次波动方程的近似解,然后基于这种近似的本征模获得天线激励的完备解,这种方法主要被美国学者所采用。而俄罗斯学者则是从经典的球谐级数解和散射迭加原理出发,运用Watson变换,将天线辐射场的球谐级数解变换到复平面上的围线积分,然后从中分离出横向的特征模式解。这两种处理方法本质上是等效的,可以通称为模式理论。由球面波导模式理论得到的计算公式中,含有待定本征值的特殊函数,只有在一定条件下,才能导出本征值及特殊函数的近似表达式。
除了解析方法之外,作为一种典型的电磁场数值算法,时域有限差分法(FDTD)[3-5]也开始应用极低频电磁场的模拟中。FDTD以差分原理为基础,直接从Maxwell方程出发,将其转换为差分方程组,在一定体积内和一段时间上对连续电磁场的数据取样。因此,它是对电磁场问题的最原始、最本质、最完备的数值模拟,具有最广泛的适用性。FDTD算法简单直观、容易掌握。从Maxwell出发,不需任何导出方程,避免了使用更多的数学工具,使得它成为所有电磁场计算方法中最简单的一种。其次,它可以在计算机所能提供的离散数值时空中仿真再现电磁现象的物理过程,非常直观,易于可视化显示。
本文基于积分形式的Maxwell方程,推导了大地—电离层谐振腔中的FDTD迭代方程,计算了极低频电磁波的辐射和传播过程,得到了可视化的结果。
1 FDTD的剖分和时间步进迭代公式
对于ELF频段,电离层高度远小于波长,因此可近似认为场沿高度方向没有变化,这样可以简化为二维问题来处理[6-8]。对于地球表面。用经纬线进行剖分是比较方便的,如图1所示。可见这种剖分得到的离散网格是非均匀,越靠近南北两极,沿纬线方向的网格长度越小。
设沿经线方向的剖分单元数为M,沿纬线方向的剖分单元数为2×M,沿纬线方向的网格编号为i,沿经线方向的网格编号为j,网格编号的参考点位于网格中心。沿纬线方向的网格长度为Δw-e,沿经线方向的网格长度为Δs-n,网格面积为S。
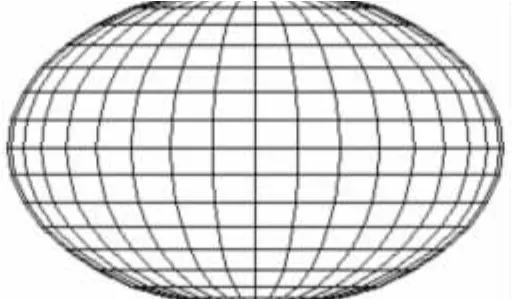
图1 地球表面剖分网格Fig.1 Earth’s surface mesh
在各向同性无源空间中,Maxwell旋度方程为:
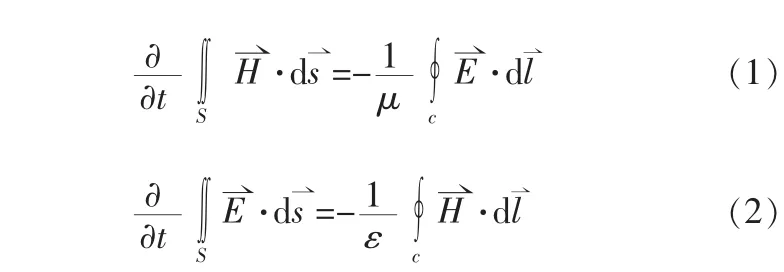
安培定律式(2)中的面积分和环路积分可近似为:
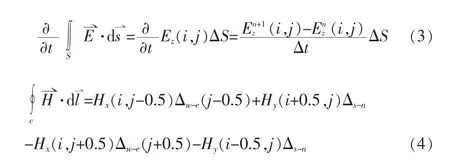
从而可以得到Ez的差分方程为
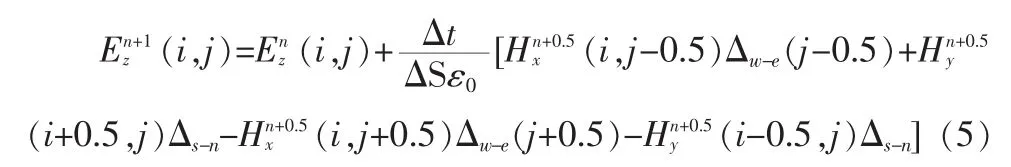
电磁感应定律式(1)中的面积分和环路积分可以近似写作:
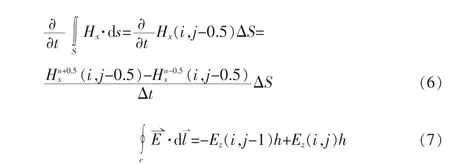
其中h为电离层高度,于是可以得到Hx的差分方程为:
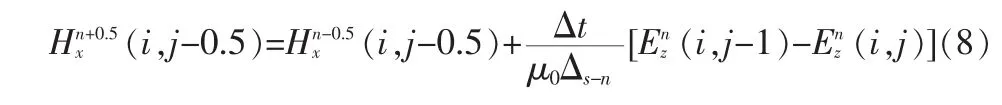
同样可以得到Hy的差分方程为
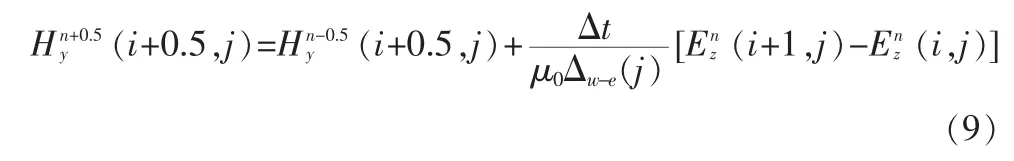
在南北两极上,四边形网格退化为三角形,此时差分方程变为:
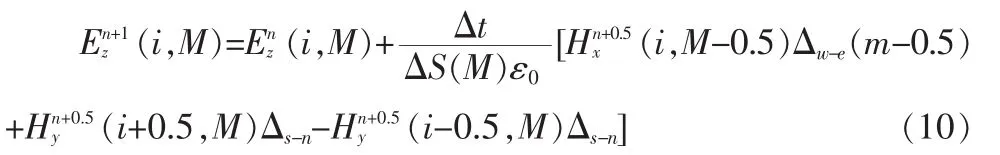
当存在电流源时,安培定律变为:
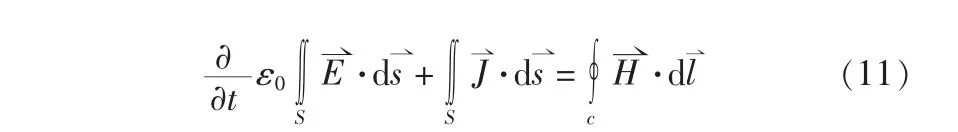
其差分近似形式为:
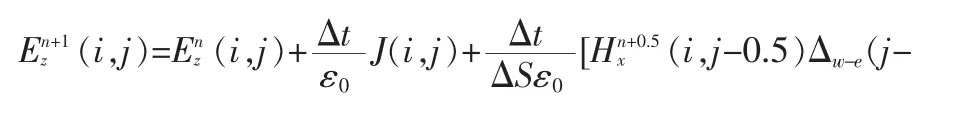
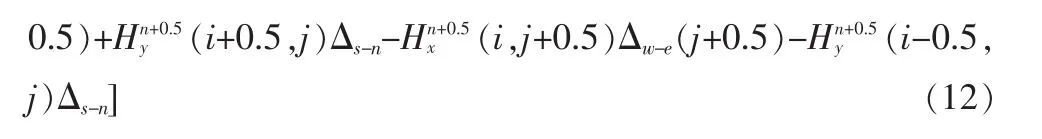
在靠近南北两极时,沿经度方向与沿纬度方向的网格长度差距将越来越大,将会影响到数值计算的稳定性和计算效率,因此实际编程中需仔细处理,合理选择时间步进。
2 计算示例
2.1 简谐振荡电流源在地-电离层波导中激励的场
假设在武汉地区(约北纬30度,东经110度)设置一个简谐振荡的垂直电流源,频率为100 Hz。计算了不同时刻球面上电磁场的分布状况,如图3~5所示。在二维平面示意图中,下边缘对应北极,上边缘对应南极,左边缘对应经度的0度。时间步进为 5 μs。
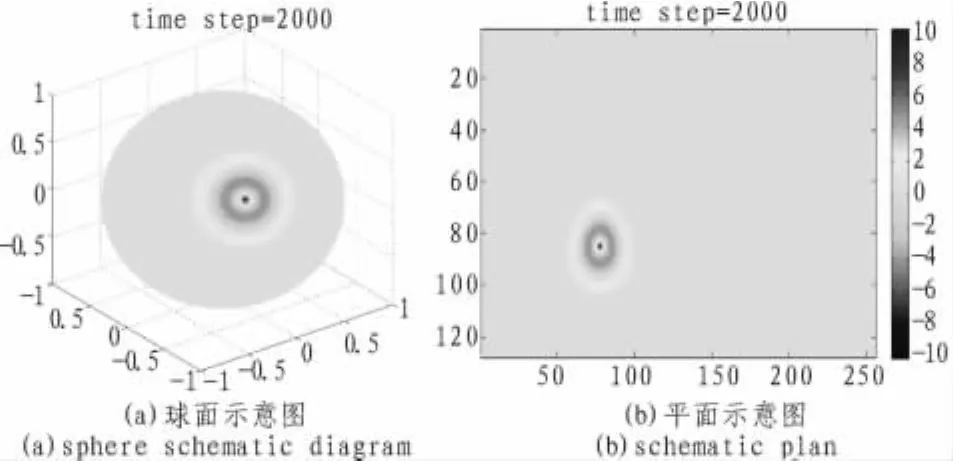
图2 一个周期时的球面电磁场分布示意图Fig.2 A cycle of spherical electromagnetic field distribution diagram

图3 3个周期时的球面电磁场分布示意图Fig.3 Spherical electromagnetic field distribution diagram of three cycles
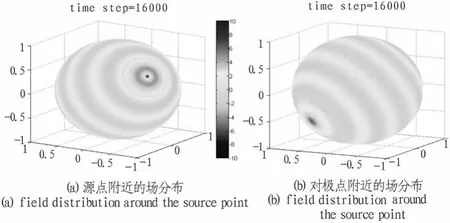
图4 8个周期时的球面电磁场分布示意图Fig.4 Spherical electromagnetic field distribution diagram of eight cycles
图2为1个周期时的场分布,可见电磁场以源点为中心,均匀地向四周扩散开来。
图3为3个周期时的电磁场分布图,此时电磁波已越过北极地区,可见时间步进迭代过程是稳定的。
图4为8个周期时的电磁场分布图,此时,电磁波已到达对极点,可以看出经球面传播后,电磁波汇聚到对极点,从而在对极点附近形成一个强信号区域。
2.2 高斯脉冲电流源在地-电离层波导中激励的场
雷电等自然极低频信号源可用高斯脉冲来模拟,将上例中的简谐源换成高斯脉冲,重新计算了电磁场的分布。图5为迭代了50 000步后电磁场的分布图。此时激励源信号早已消失,但地-电离层腔体中仍有稳定的电磁波存在,这表明地-电离层波导中存在谐振现象。图6为对极点电场强度随时间的变化曲线,可以看出两次正的峰值之间的时间间隔约为0.13 s,由此可以估算出地-电离层腔体的谐振频率约为7.7 Hz。这个数值与有关文献给出的地球舒曼(Schumem)谐振的基波谐振频率十分接近。
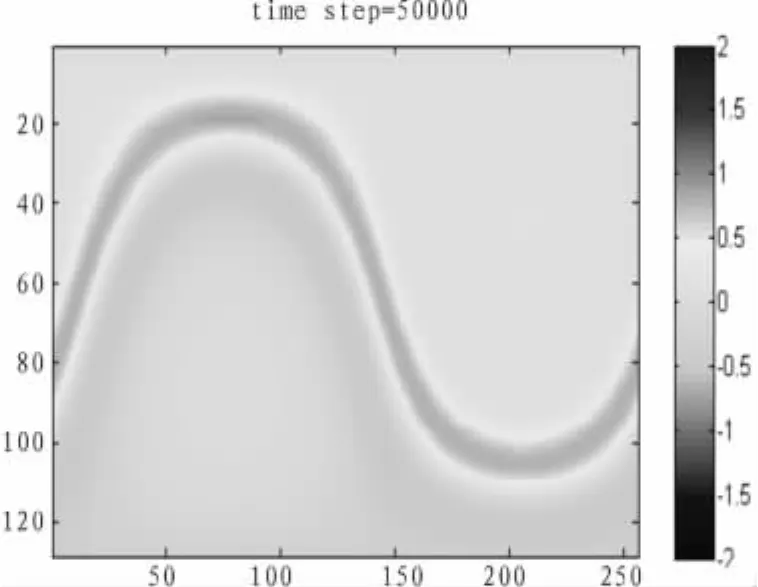
图5 高斯脉冲信号激励的球面电磁场分布示意图Fig.5 Spherical electromagnetic field distribution diagram with Gauss pulse signal excitation

图6 对极点电场的时域波形Fig.6 Electric field waveform in time domain on pole
3 结束语
文中采用FDTD方法计算了ELF电磁场在地-电离层波导中的分布,并给出了可视化的结果。从计算结果来看,大地-电离层腔体中的ELF电磁场衰减很小,而且球面波导结构可以将电磁波汇聚到天线的对极点,使得对极点附近成为强电磁场区域。从高斯脉冲源的FDTD计算结果来看,大地-电离层腔体在极低频段存在谐振点,可以观察到明显的舒曼(Schumem)谐振效应。
由于缺乏全球的大地及电离层参数,在本文的计算中,暂时没有计入大地和电离层电导率的有限性和非均匀性。但FDTD是一种基于差分方程的算法,适合于处理媒质的非均匀性问题。只要建立了各个地区的大地电导率及电离层电子浓度数据库,应用该方法就可以模拟出极低频电磁场在全球的传播与分布。
[1]潘威炎.长波、超长波、极长波传播[M].成都:电子科技大学出版社,2004.
[2]Wait J R.Electromagnetic wave in stratified media[M].London:Pergamon press,1962.
[3]王秉中.计算电磁学[M].北京:科学出版社,2002.
[4]王长华,王秩雄.基于时域有限差分法的谐振腔分析[J].现代电子技术,2011(2):103-105,108.
WANG Chang-hua,WANG Zhi-xiong.Analysis of cavity resonator based on finite difference time domain[J].Modern Electronics Technique,2011(2):103-105,108
[5]肖健,高爱华.飞秒激光触发光电导天线产生太赫兹波的研究[J].电子科技,2010(3):7-9.
XIAO Jian,GAO Ai-hua.Investigation of generation of terahertz with the photoconductor triggered by the femosecond laser pulse[J].Electronic Science and Technology,2010(3):7-9.
[6]Burrows M L.ELF Communications antennas[J].Peter Peregrinus Ltd.1978.
[7]Simpson J J,Taflove A.Two-dimensional FDTD model of antipodal ELF propagation and Schumann resonance of the earth[J].IEEE Antennas and Wireless Propagation Letters,2002(1):53-56.
[8]Simpson J J,Taflove A.Three-dimensional FDTD modeling of impulsive ELF propagation about the earth-sphere[J].IEEE TransactionsonAntennasandPropagation,2004(52):443-451.
