工程岩爆灾害判别的RBF-AR耦合模型

王 羽，许 强，柴贺军，刘 丽，夏毓超，王晓东

1.重庆交通大学国际学院，重庆 400074

2.成都理工大学地质灾害防治与地质环境保护国家重点实验室，成都 610059

3.招商局重庆交通科研设计院有限公司，重庆 400067

0 引言

岩爆是岩体中聚积的高弹性应变能大于岩石破坏所消耗的能量时，多余的能量导致岩石爆裂，使岩石碎片从岩体中剥离、崩出、弹射的动力破坏现象。由于围岩是一个开放的复杂系统，其稳定性受地质和工程等多种因素综合影响，这些因素有的是确定性的，有的则具有随机性、模糊性和可变性等不确定特点。

近年来，学者们针对锦屏二级水电站长隧洞群等典型工程的岩爆现象与机理进行了广泛探索，取得了部分成果：W.D.Ortlepp[1]根据完整岩体的裂隙化及原有裂隙面的滑移程度将岩爆分为应变型和断裂型；R.S.Read[2]利用加拿大 AECL地下实验室采用声发射、微震、应力、变形及声波多元化技术分析硐室围岩的片帮形成过程；王元汉等[3]提出了用模糊综合评判法进行岩爆判别，但模糊综合评判法权重的赋予常带有专家的主观性，缺乏足够科学的模型描述；杨莹春等[4]、陈祥等[5]运用物元可拓法确定岩爆指标和等级标准，并给出分级预报模型，但在计算关联度时往往把最优点考虑为区间中点，容易忽视其他的约束条件，致使最终评价结果有所偏离实际；姜彤等[6]通过灰色归类法对南水北调西线工程岩爆风险评估进行应用，但当原始数据方差较大、信息过于分散时，就不能保证预测精度与效度；宫凤强等[7]根据岩爆发生和烈度分级，采用距离判别方法预测岩爆发生方式与时点，不过，距离判别法会受原始数据准确性、代表性的影响，容易出现较大误差。

RBF-AR（radias basis function-autoregression）模型[8-10]，是 RBF（高斯径向基函数）网络和线性AR模型结构组成的复合结构。它是一种用RBF来逼近AR函数系数的非线性预测方法。RBF网络具有拓扑结构简单、能精确地逼近非线性动态特性以及快速训练参数的特点。AR（自回归模型）能很好地描述非线性系统的动态特征。RBFAR模型融合了RBF辨识参数的优点和AR描述非线性系统的动态特征的能力。此外RBF-AR模型是一个全局模型，它需要的RBF中心少，模型参数采用寻优辨识，克服了工程建模中参数辨识可能出现的局部化问题。

1 RBF-AR算法模型

1.1 模型结构

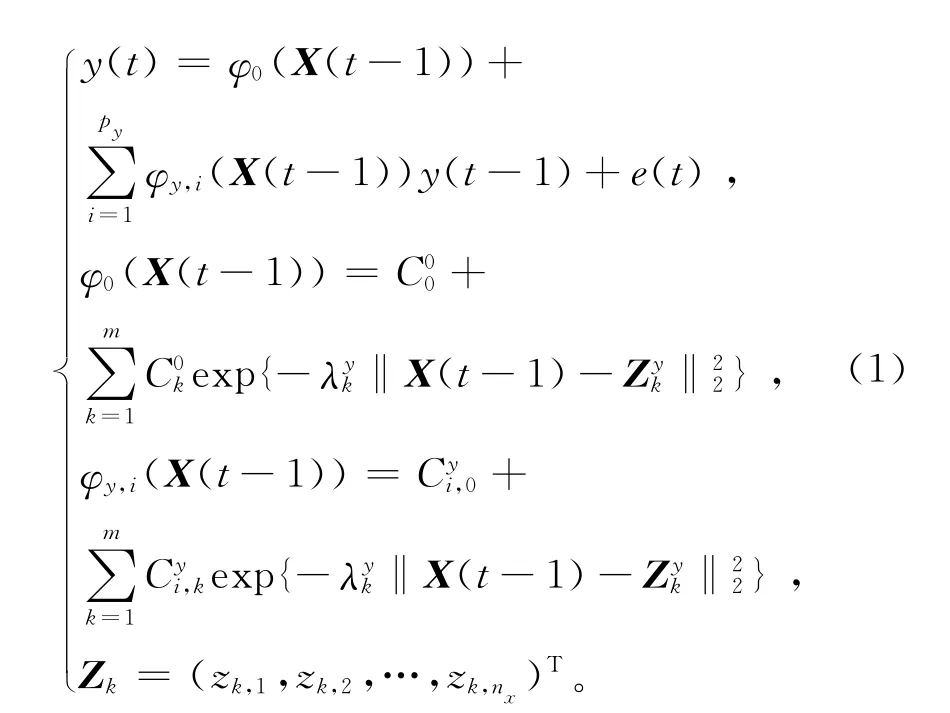
式中：py、m 和nx是模型阶次，nx＝dim｛X（t-1）｝；φ0、φy，i是依存于状态的模型系数，它取决于 RBF网络结构；Zk（k＝1，2，…，m）是 RBF网络的中心，是RBF网络参数，是缩放比例参数；e（t）为白噪声；是初始标量，（k＝0，1，2，…，m）和（i＝1，2，…，p；k＝0，1，2，…，m）是标量，‖·‖代表矢量的2范数，y（t）是最终模型输出，y（t-1）为网络自变量，X（t-1）为状态变量，X（t-1）＝[y（t-1），…，y（t-nx）]，决定时变模型参数的状态变量X（t-1）是输出信号。

1.2 模型估计方法

RBF-AR模型的辨识包括估计模型中所有的参数和阶次的选择。因此必须建立一个合适的参数优化方法，然后用不同的阶次重复实验，最终选择最好的模型。在本文中，采用结构化非线性参数优化方法。这种方法把被搜索参数划分为线性参数空间和非线性参数空间，用最小二乘（LSM）来优化模型中的 线 性 参 数，用 （LMM，levenberg-marquardt method）方法来优化非线性参数，利用该方法能大幅度提升计算精度。该方法的优化过程按如下步骤进行。

1.2.1 参数类型划分

将式（1）的所有参数进行线性参数和非线性参数分类，线性参数θL和非线性参数θN分别用下式表示：

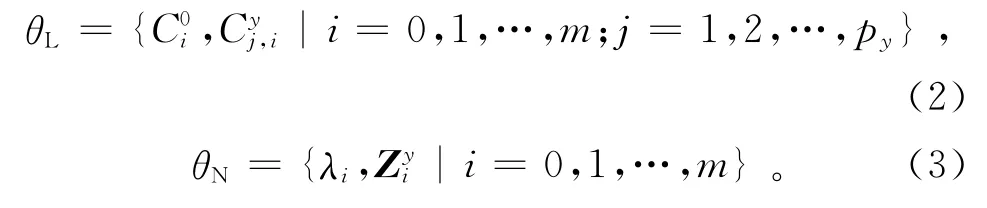
这样模型（1）就可以转换成式（4）的形式：

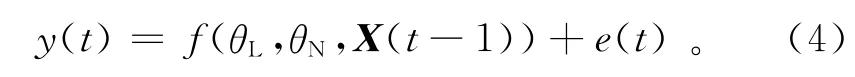
式（2）中θL包含了RBF-AR模型的所有线性参数，式（3）中θN包含了所有非线性参数，求出θL和θN就可以确定模型的各计算参数了。

1.2.2 参数优化

一般运用二次目标函数进行参数优化，即

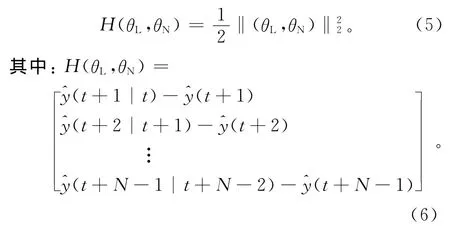
N为序列数，在式（4）的基础上，RBF-AR模型的向前一步预测为

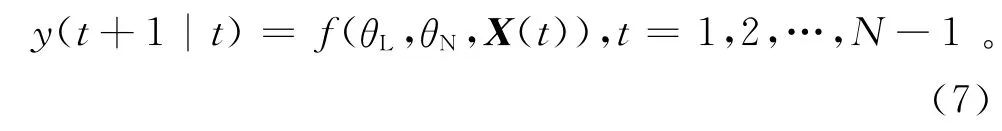
可以看出，此优化问题就是计算

1.2.3 模型阶次的确定

RBF-AR模型的阶次包括Py、nx和m。模型阶次按照AIC值来确定。通过寻找式AIC值最小并且模型动态特性合适的值作为Py、nx的模型阶次。RBF-AR模型的AIC值可以表示为

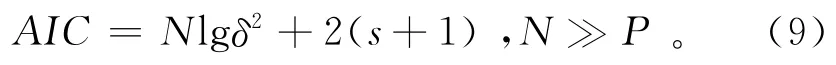
式中：AIC是Akaike信息标值；P是回归部分的最大阶次；s是要辨识的线性参数和非线性参数个数之和；δ2为方差。

2 基于岩爆机理与主控要素的RBF-AR模型

2.1 岩爆机理解析

现代工程与试验研究表明，岩爆是洞室围岩剧烈破坏的现象体现，其机理可以理解为：在开挖卸荷作用下，初始应力场使硬质脆性岩体储聚的弹性应变能瞬间释放，出现围岩应力集中；致使超过岩体内摩擦力及黏聚力而产生张-剪脆性破坏，伴随震动和声响，在消耗部分弹性应变能的同时，将剩余的能量转化为岩块的动能，使围岩急剧向动态失稳发展，造成岩片脱离母体，向临空方向猛烈抛掷弹（散）射。

岩爆产生过程揭示，形成岩爆的基础条件是高地应力与围岩二次应力集中。人工开挖洞室，不可避免会对围岩初始应力状态产生扰动，在一定程度上影响初始应力平衡状态，出现围岩应力重分布，而二次应力在局部位置的高度集中，导致围岩应力超过岩爆的临界应力，发生岩爆破坏。

不过，国内外众多工程实践证明，岩爆是多因素复杂作用的结果。围岩应力的高度集中不是出现岩爆的唯一主控要素。岩石强度、围岩岩性、储能条件等因素均起关键作用。徐林生等[11]发现二郎山隧道岩体只有在岩石弹性能量指数Wet和高地应力这两条件均满足一定标准时才可能发生岩爆。谷明成等[12]提出要同时满足岩体抗压抗拉比Rc／Rt≥15、岩石弹性能量指数Wet≥2.0、围岩切向应力与抗压强度比值σθ／Rc≥0.3、岩体完整性指数Kv≥0.55共4个标准时方能出现岩爆。

2.2 岩爆强度与主要影响因素的关系

根据岩爆机理可以将岩爆的产生分为内因和外因两方面：内因包括岩石的强度与变形特性、岩体结构特性和地质构造特征等几个方面；外因包括围岩的应力或能量。针对以上影响岩爆的主要因素，提出3类判别准则：

1）围岩的岩性与岩爆的产生密切相关，可采用围岩抗压强度σc与抗拉强度σt的比值B来判别，B＝σc／σt，B越小，则岩爆发生的概率和强度越大。B＞40.0时，无岩爆；B＝26.7～40.0时，弱岩爆；B＝14.5～26.7时，中等岩爆；B＜14.5时，强岩爆。

2）Burton[13]发现切向应力对岩爆的产生具有直接影响，提出了根据围岩切向应力与围岩抗压强度的比值σθ／σc来判定岩爆强度，比值越大，则岩爆发生的概率和强度越大。

3）岩爆的产生与能量有关，围岩中积聚的弹性应变能是岩爆发生的内部主导因素。Kidybinski[14]定义了岩石弹性能量指数Wet，并用来预测岩爆，其值越大，破坏时释放的能量越大，岩爆存在的可能性及其烈度就越大。为了有效预测和判别隧道工程岩爆灾害，在总体考虑岩爆各影响因素的基础上，选取隧道工程中岩体完整性指数Kv、围岩抗压强度σc、岩石单轴抗拉强度σt、围岩最大切向应力σθ、围岩抗压强度与其抗拉强度的比值σc／σt、围岩切向应力与围岩抗压强度比值σθ／σc、岩爆能量倾向性指数Wet作为岩爆预测的评判指标，如表1所示。

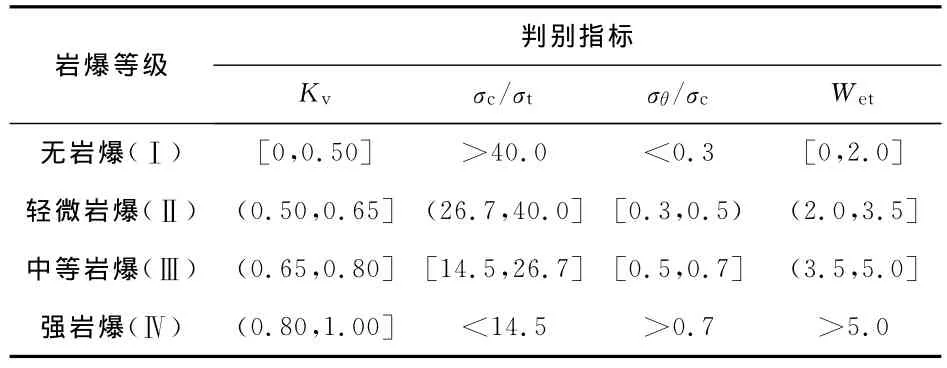
表1 岩爆判别等级标准Table1 Classification criterion of rock burst

2.3 模型阀值设定与调试

由于RBF-AR计算值为[0，1]的实数，根据计算规则和程序，可设定的岩爆烈度分级阀值区间，如表2所示。

表2 RBF-AR计算阀值Table2 Classification threshold value of RBF-AR

根据上节所述RBF-AR模型，在MATLAB环境下编制了岩爆判别程序。将17个工程实例作为RBF-AR（py，m，nx）训练样本，将其数据输入判别程序，通过学习和试算，最终确定出RBF-AR（py，m，nx）模型参数。Akaike信息标值AIC＝102.62，模型阶数py＝17，维数nx＝42，模型系数φ0＝2.83，φy，i＝0.62，缩放比例参数λk＝0.12，节点数目m＝4，参数个数s＝25，迭代次数t＝380次。同时，模型特征阀值与变量区间如表3所示。

为了验证其有效性，选取4个地下工程实例作为检测样本。根据特征计算值判断岩爆灾害等级，评判结果和对比情况列于表4。从表4中的对比情况可以看出，RBF-AR模型计算结果与实际情况几乎完全相同，同时，经过学习检验后，运用训练好的岩爆预测模型对终南山隧道竖井岩爆发生趋势情况进行了预测。

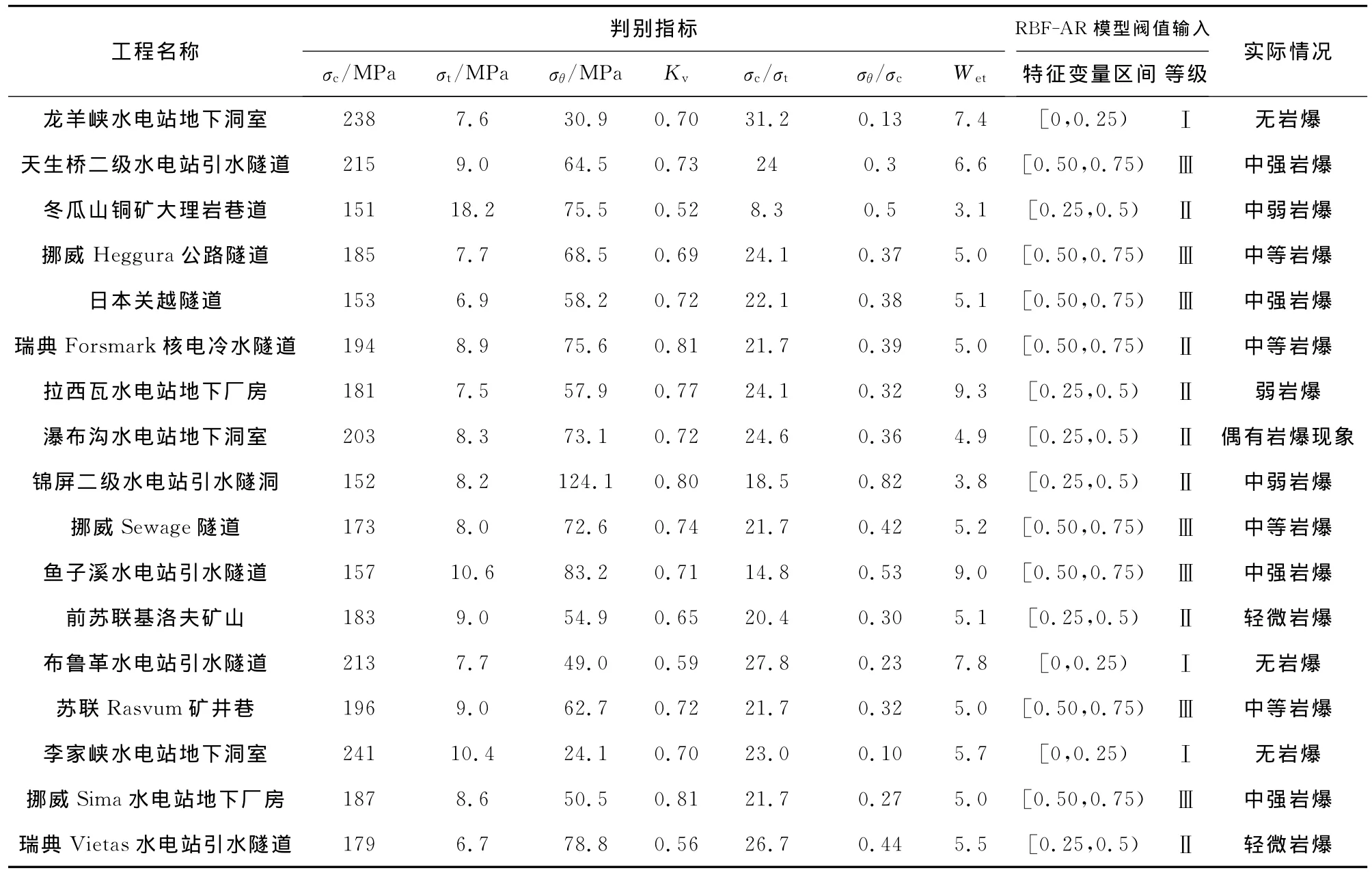
表3 国内外地下工程岩爆分析结果Table3 Rockburst analysis results of some underground rock project

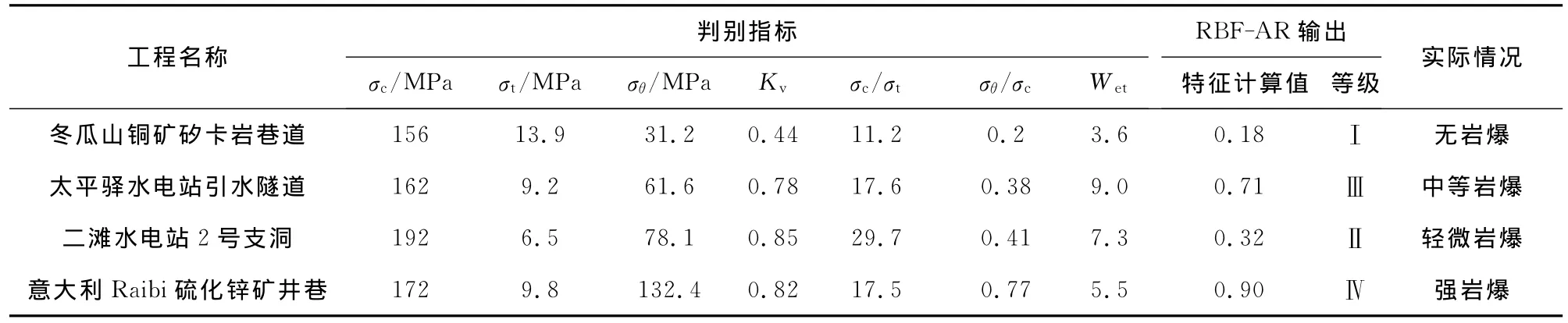
表4 工程实例判定检测表Table4 Engineering judgements testing table

3 方法验证与工程实例

3.1 工程概况

秦岭终南山公路隧道全长18.02km，该隧道是国家高速公路网包头至茂名线控制性工程。为了改善运营环境条件及安全性，采用了3座竖井的纵向式通风方案。该方案是目前世界口径最大、深度最大的竖井通风工程，此隧道通风竖井被形象地形容为地球上最大的“烟囱”（图1，2）。竖井主体采用中隔板将送排风道分开，竖井底部送风和排风设不同高度的导流板，以利于风流的汇合和分流[14]。各竖井风塔设计高度均为40m，排风口下沿按高于进风口上沿15m设计，3个竖井分别将东线、西线两隧道分成4个通风段，最长段为4.948km，最短段为3.781km。其中2号竖井是该隧道通风系统主体工程，也是国内乃至世界公路隧道规模最大的竖井工程，该竖井为进、回风合一的通风井（图3），其位于秦岭北坡水洞子沟中上游右侧30m，竖井中心地面高程1703m，竖井内径为11.2m，最大开挖外径为13.32m，井深为661m。2号竖井通过的地层：上部30m为第四系全新统坡洪积层，其中，表层为崩积块石土，块石土岩性为混合片麻岩，Ⅱ类围岩；下部为混合片麻岩，部分地段夹黑云母斜长角闪片岩残留体，岩体受构造影响轻微，岩体完整，Ⅵ类围岩。在竖井埋深大的地段，最大水平主应力测试值为21.04MPa，方向NW28°，属于高地应力水平，可能会产生岩爆。

3.2 模型应用

表5为终南山隧道竖井工程岩爆采集的实测岩体力学参数。利用RBF-AR法对其岩爆烈度进行了预测，判别结果与实际情况完全一致，表明RBFAR法在实际工程岩爆预测中的有效性和可靠性，为岩爆预测提供了一条新的途径。

3.3 工程防治方法与施工手段

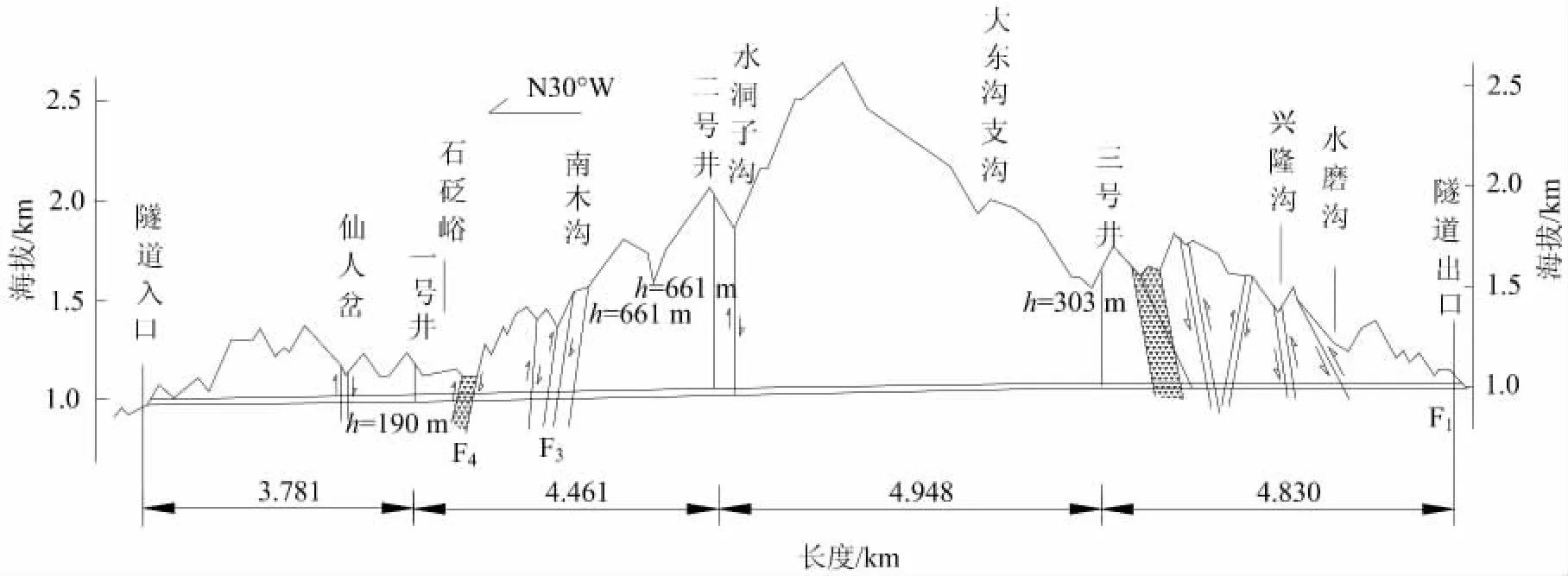
图1 秦岭终南山隧道通风竖井位置图Fig.1 Locations of ventilation shafts in Zhongnanshan tunnel

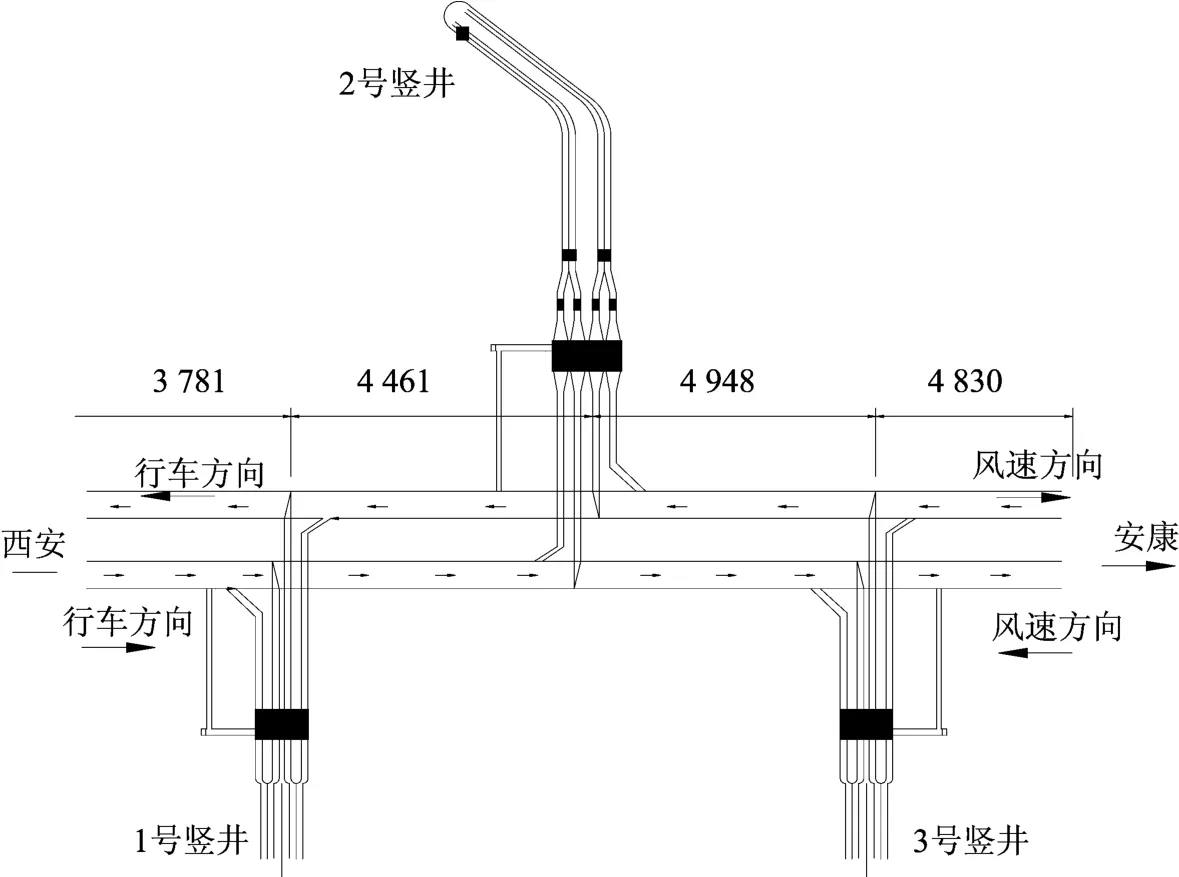
图2 秦岭终南山公路隧道通风方案图Fig.2 Ventilation shaft plan of Zhongnanshan tunnel

终南山公路隧道2号通风竖井的岩爆现象时有发生，在全面分析判断的基础上，提出了“预防为先、安全第一、减少扰动、实时监控”的施工原则。终南山公路隧道2号通风竖井采用导坑扩挖法和中心扩孔技术相结合进行施工。运用竖井专用机械从底部开始向上将导孔扩大至竖井设计尺寸，弃碴从孔洞向下排出，最后从底部由下至上施做防水层与二次衬砌。使用竖井双层吊盘，强化保护能力（图4）。在下层盘预备多个安全绳梯，一旦下部围岩出现岩爆现象，工人可及时通过安全梯到达吊盘上躲避，等待升井。在进行钻眼等作业时，采用铁丝网罩盖住吊盘喇叭口，防止井壁上部松散岩块坠入施工作业面。尽量避免大规模钻眼爆破，严格控制周边孔的装药量，采用小直径、低爆速药卷，按照中部掏槽孔-辅助孔-周边孔的毫秒时间微差顺序起爆，防止应力重分布导致的应力集中。同时，中弱岩爆发生地段，需采取及时有效的支护手段，见表6。

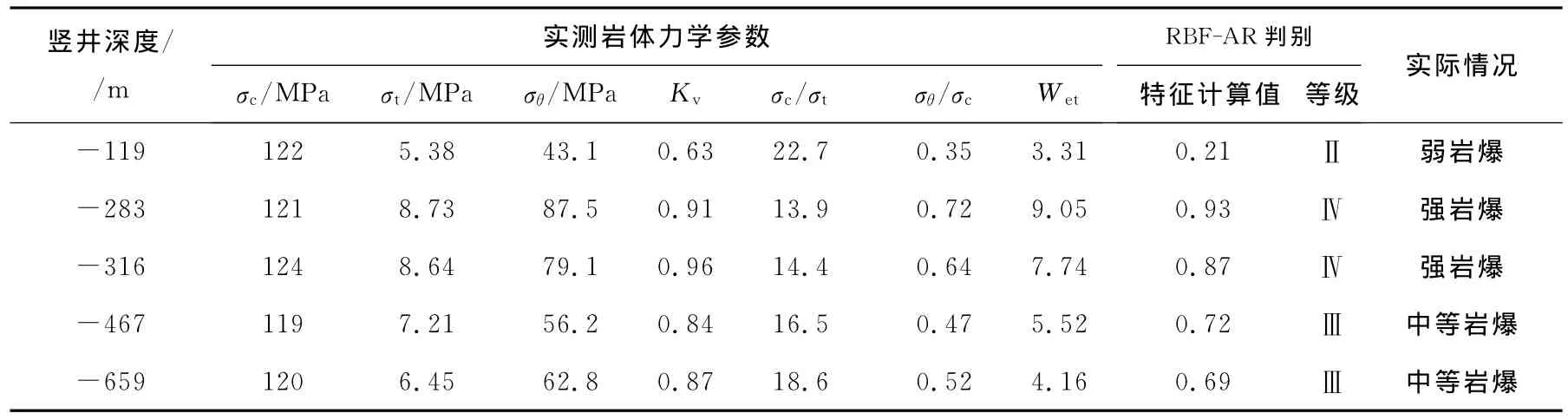
表5 终南山隧道竖井工程岩爆实测数据与判测结果Table5 Measured data for rock burst and prediction of Zhongnanshan tunnel ventilation shaft

表6 岩爆地段支护参数Table6 Supporting parameters in rockburst area

图3 2号竖井井塔Fig.3 Derrick of No.2ventilation shaft

图4 吊盘安装Fig.4 Photo of crane installation

4 结语

1）岩爆是一种复杂的动力失稳现象，对其进行预测难度较大。笔者提出基于非线性参数优化的RBF-AR岩爆预测模型，作为一类变系数模型，描述岩爆在相空间中的演化轨迹，是该算法在此研究方向上的一次探索性尝试。工程实例中，采用RBFAR模型进行的岩爆判定结果与实际情况吻合度较高，证明本文算法具有很强的计算能力。运用此模型，能较客观地反映岩爆灾变状况，为采取必要的措施进行断链减灾提供依据。

2）研究表明，RBF网络输入变量的选择对预测结果有重大影响，如何选择状态向量的最优组合是未来进一步提升此模型运算精度和效率的关键，这不仅需要一定的数学技巧，更依赖于对岩爆本质和影响因素的认识。同时，随着样本数量的增多，RBF-AR岩爆预测模型的预估效果和预估精度将会得到更大的提升。

（References）：

[1]Ortlepp W D.Rock Fracture and Rockbursts：An Illustrative Study[M].Johannesburg：South African Institute of Mining and Metallurgy，2009：23-67.

[2]Read R S.20Years of Excavation Response Studies at AECL Sunderground Research Laboratory [J].International Journal of Rock Mechanics and Mining Sciences，2004，41（8）：1251-1275.

[3]王元汉，李卧东，李启光，等.岩爆预测的模糊数学综合评判方法[J].岩石力学与工程学报，1998，17（5）：493-501.Wang Yuanhan，Li Wodong，Li Qiguang，et al.Method of Fuzzy Comprehensive Evaluations for Rock Burst Prediction [J].Chinese Journal of Rock Mechanics and Engineering，1998，17（5）：493-501.

[4]杨莹春，诸静.一种新的岩爆分级预报模型及其应用[J].煤炭学报，2000，25（2）：169-172.Yang Yingchun，Zhu Jing.A New Model for Classified Prediction of Rockburst and Its Application[J].Journal of China Coal Society，2000，25（2）：169-172.

[5]陈祥，孙进忠.岩爆判别指标和分级标准及可拓综合判别方法[J].土木工程学报，2009，42（9）：82-87.Chen Xiang，Sun Jinzhong.Judgment Indexes and Classification Criteria of Rock-Burst with the Extension Judgment Method [J].China Civil Engineering Journal，2009，42（9）：82-87.

[6]姜彤，黄志全，赵彦彦.动态权重灰色归类模型在南水北调西线工程岩爆风险评估中的应用[J].岩石力学与工程学报，2004，23（7）：1104-1108.Jiang Tong， Huang Zhiquan， Zhao Yanyan.Dynamically Weighted Grey Optimization Model for Rockburst Risk Forecasting and Its Application to Western Route of South-North Water Transfer Project[J].Chinese Journal of Rock Mechanics and Engineering，2004，23（7）：1104-1108.

[7]宫凤强，李夕兵.岩爆发生和烈度分级预测的距离判别方法及应用[J].岩石力学与工程学报，2007，26（5）：1012-1018.Gong Fengqiang，Li Xibing.A Distance Discriminant Analysis Method for Prediction of Possibility and Classification of Rockburst and Its Application[J].Chinese Journal of Rock Mechanics and Engineering，2007，26（5）：1012-1018.

[8]Priestley M B.State Dependent Models：A General Approach to Nonlinear Time Series Analysis[J].Journal of Time Series Analysis，1980，23（1）：57-71.

[9]Muler W.Proceedings of Information Processing[C]／／Vesin J.An Amplitude Dependent Autoregressive Signal Model Based on a Radial Basis Function Expansion.Minnesota：Proceedings of International Conference of ASSP，1993：129-132.

[10]Shi Z，Tamura Y，Ozaki T.Nonlinear Time Series Modeling with the Radial Basis Function Based State Dependent Autoregressive Model[J].InternationalJournal of System Science，1999，30（7）：717-727.

[11]徐林生，王兰生.二郎山隧道岩爆岩石力学试验研究[J].公路，2000，25（12）：6-8.Xu Linsheng，Wang Lansheng.Research on Rock Mechanical Experiment of Rock Burst in Erlangshan Tunnel[J].Highway，2000，25（12）：6-8.

[12]谷明成，何发亮，陈成宗.秦岭隧道岩爆的研究[J].岩石力学与工程学报，2002，21（9）：1324-1329.Gu Mingcheng，He Faliang，Chen Chengzong.Study on Rockburst in Qinling Tunnel[J].Chinese Journal of Rock Mechanics and Engineering，2002，21（9）：1324-1329.

[13]Barton N.Some New Q-Value Correlations to Assist in Site Characterisation and Tunnel Design[J].Journal of Rock Mechanics ＆ Mining Sciences，2002，39：185-216.

[14]Kidybinski.Strata Control in Deep Mines[M].[S.l.]：A A Balkema Press，1990.