基于岩石地质本质性的碳酸盐岩单轴抗压强度预测

鲁功达，晏鄂川，王环玲，王雪明，谢良甫

1.中国地质大学工程学院，武汉 430074

2.河海大学海岸灾害及防护教育部重点实验室，南京 210098

3.河海大学岩土工程研究所，南京 210098

0 引言

单轴抗压强度是岩土工程中岩石的基本参数，室内单轴压缩试验是其最简单的测定方法，这种试验要求所使用的样品必须是具有特定尺寸的完整岩心。然而，在岩体软弱、破碎或者岩层厚度较小时，取得符合要求的岩心则较为困难，加之岩石的非均质性导致其强度值差异明显，因此人们便采用经验公式来估算岩石的单轴抗压强度。目前国内外有很多学者通过测定试样的回弹值、波速、密度等指标，以无损的方法预测完整岩石的单轴抗压强度，同时随着人工智能和计算机数值模拟技术的发展，岩石抗压强度的预测方法也趋于多样化。邓华锋等[1]考虑回弹值和纵波波速，采用线性回归的方法对砂岩的单轴抗压强度进行了预测研究；Heidari等[2]通过试样不同方向的点荷载试验，也采用回归的方法对石膏的单轴抗压强度和抗拉强度进行预测研究。由于不能完全了解各因素对岩石单轴抗压强度的影响，Sarkar 等[3]、杨 文 甫 等[4]、Dehgha 等[5]、Zorlu等[6]分别考虑岩石密度、矿物组成、矿物粒度及形态、空隙度、纵波波速等指标，采用神经网络的方法对多类岩石的单轴抗压强度进行了预测研究。基于颗粒离散元程序，王新等[7]考虑不同的土石比和各级粒径下石料的不同黏结强度，用PFC模拟得出了相应土石混合体在不同围压下的抗压强度；Tawadrous等[8]考虑不同材料的接触黏结力、刚度和颗粒大小等模型细观参数，用PFC模拟得出了材料的单轴抗压强度值，并采用神经网络的方法，以上述细观参数为输入层单元对模拟所得强度值进行了预测研究。

上述研究中，数值试验类方法中的细观参数具有较大的不确定性，不易在工程实践中推广；其次，以上研究均未系统论证所选指标的依据及其合理性，各自所考虑的强度影响因素也不够全面，而且均未考虑水的影响，亦或所选指标具有片面性，不能代表试样整体的特征。

王思敬[9]指出，岩石力学的研究对象是岩石，虽然研究目标是探讨岩石的力学性能及其工程行为，但是却与其他工程材料有所不同，因为岩石都经历了特定的地质演化历史并具有特殊的地质本质性。因此，岩石力学研究都应该在充分认识岩石的地质本质性的基础上开展。

笔者以碳酸盐岩这类工程中常见、成分相对简单（主要为碳酸盐和黏土矿物）的沉积岩为例，充分全面地考虑其地质本质性，并据此选取适当的无损物理指标，采用回归和神经网络的方法对其单轴抗压强度展开预测研究，最后采用灰色关联分析法验证本次研究所选用的预测指标的合理性。

1 单轴抗压强度预测的基本指标

文献[9]指出，岩石的地质本质性涵盖了岩石的物质性、结构性和赋存状态3个方面的内容。岩石的物质性是指原岩物质及其次生演化，岩石矿物组分力学特性的差异直接影响着岩石的力学性能及其不均一性；岩石的结构性包括不同尺度结构体的形态和排列，以及它们之间的连接特征，主要表现为地质体的原生结构、次生结构和构造断裂等方面，地质体的各向异性就是其结构性的体现；赋存性是岩石区别于其他人工材料的重要特征，包括岩石所处地应力环境、地下水环境和地质动力环境3方面。

对比前人用于预测岩石强度所考虑的影响因素，同时考虑到岩石的地质本质性，笔者对碳酸盐岩单轴抗压强度预测的基本指标参数做如下选择：首先，以碳酸盐岩矿物组成和密度反映岩石的物质性，前者体现了岩石物质组成的比例，后者则体现了单位体积岩石中各组成物质的数量；其次，由于弹性波对固体材料中微空隙、微裂隙的发育状况反应敏感，因此可以用试样的纵波波速来反映完整岩石的结构特征；而对于岩石所处的环境状态，在室内力学试验中其主要体现为给试样施加的围压和含水状态的影响，对本文所考虑的单轴压缩试验来说，只需以不同的参数来反映岩石试样的含水状态对其强度的影响。因此，在充分考虑岩石上述3方面特征及其与单轴试验的联系的基础上，本预测研究中所选用的矿物组成、密度、纵波波速和含水状态基本指标，可以比较全面的涵盖岩石的地质本质性对其自身强度的影响。

2 碳酸盐岩单轴抗压强度预测的回归方法

根据上一节中对碳酸盐岩单轴抗压强度预测基本参数的考虑，并简化碳酸盐岩矿物组成仅为碳酸钙和黏土矿物（基质），与前人提出的强度预测经验公式比较分析后，建立如下表达式进行碳酸盐岩单轴抗压强度的预测计算：

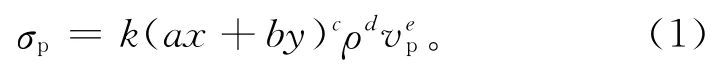
式中：σp为碳酸盐岩试样单轴抗压强度预测值（MPa）；x与y分别为试样中碳酸钙和基质的质量分数（%）；ρ 为 试 样 密度（g／cm3）；vp为纵波 波 速（km／s）；k为与试样含水状态和对水敏感性有关的影响系数（简称水影响系数）；a、b、c、d、e均为假定经验公式的待定系数。

文献[3]考虑波速、点荷载强度和密度等指标，用神经网络的方法对天然状态下灰岩的单轴抗压强度进行了预测研究；根据该文中试验结果，利用最小二乘法对式（1）进行回归处理，且由于灰岩中碳酸钙质量分数不低于95%，于是在处理过程中不妨假设试验所用灰岩的碳酸钙质量分数为95%，基质质量分数为5%。解得上式中的待定系数后有：

用（2）式对所研究灰岩的单轴抗压强度进行计算，结果见表1（试样1-10）。由计算结果可见，上述预测计算公式可以较好地反映试样单轴抗压强度与矿物组成、密度、纵波波速的关系。同时，注意到式（1）中的系数a、b实际上反映了岩石中单位含量的碳酸钙和黏土矿物对其抗压强度的贡献，而解得的a与b的比值为6.43，正好介于一般工程中涉及的纯净灰岩与黏土岩单轴抗压强度比值的范围中。因此，笔者提出的经验公式各项参数的组合形式具有较为明确的物理意义。

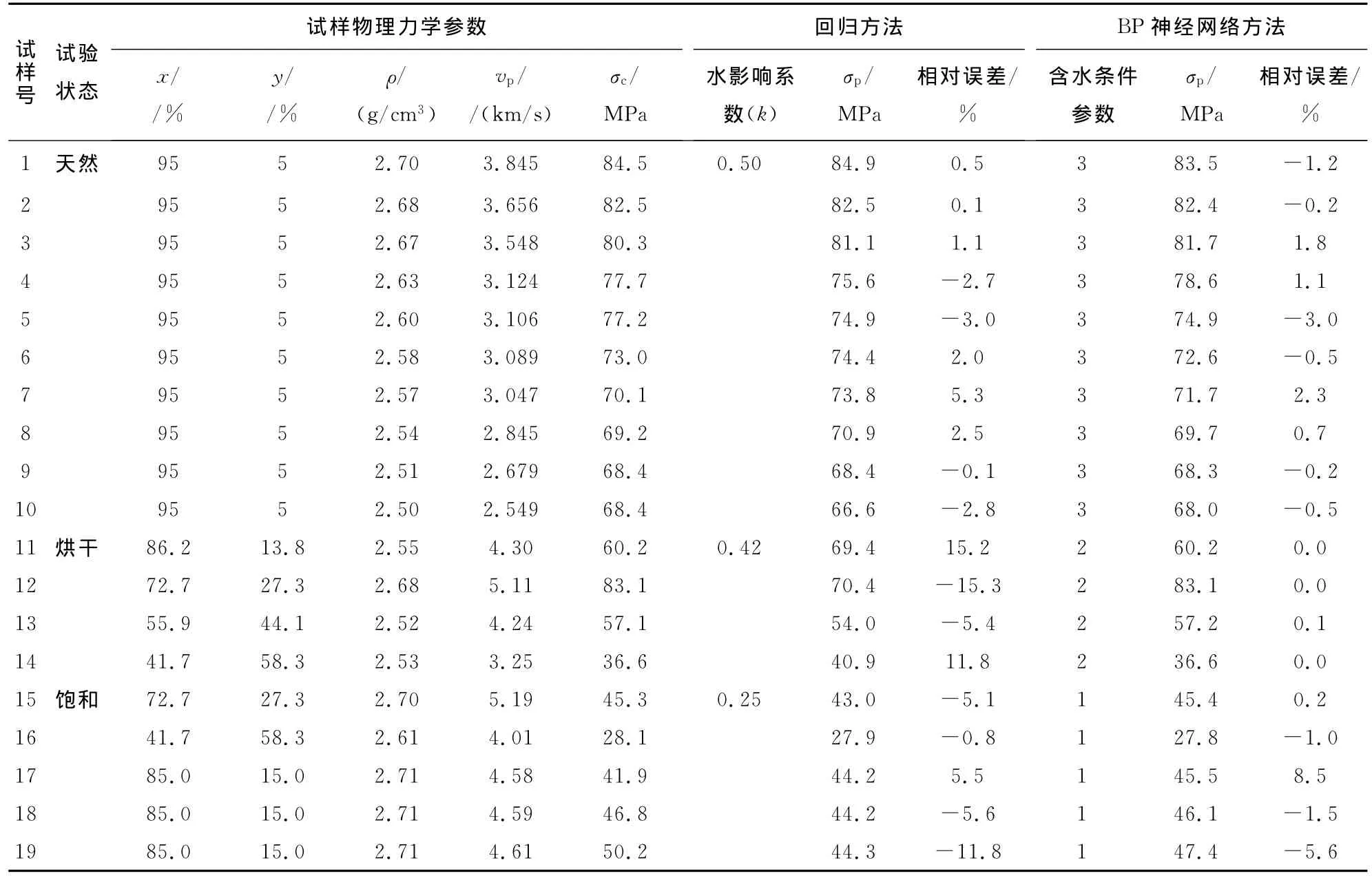
表1 碳酸盐岩单轴抗压强度预测值及其误差Table1 Predictive values of UCS of carbonate and their error

为了进一步证明（1）式具有普遍意义，用本方法对另一类碳酸盐岩——泥灰质岩石的单轴抗压强度进行了预测。张加桂[10]对三峡库区巴东组泥灰质岩石在岩溶风化作用下碳酸钙含量、密度、波速、力学强度等的变化进行了试验研究，根据该文中的部分参数（试样11-16），结合作者在巴东大坪小区某场地勘察中所取泥质灰岩试样的室内试验数据（试样17-19），利用所得经验公式对这类岩石的单轴抗压强度进行预测计算。在计算中设烘干、饱和状态下试样的水影响系数k分别为k1、k2，而a、b、c、d、e的值均保持不变（即与（2）式中的值相同），用最小二乘法解出k1（0.42）、k2（0.25）后，对试样的单轴抗压强度进行计算，结果见表1。

绘制试样单轴抗压强度实测值与回归方法预测计算值的关系曲线如图1。由图1和表1可见，上述经验公式对于碳酸盐岩类都具有较好的适用性，而表1中计算结果出现误差的原因主要为建立经验公式时假设较为简单，碳酸盐岩中的主要矿物除了方解石外，可能还含有白云石、燧石等，其基质的矿物组合也可以多种多样，而式（1）中以a、b两个系数概括试样矿物组合的强度贡献只是实际情况的简化。此外，由于泥灰质岩石具有膨胀性，在含水状态变化的情况下试样将可能出现微裂隙，这也将导致预测计算结果存在一定的偏差；而烘干状态下其水影响系数 为0.42，小于式（2）中天然状态下的k值0.5，也是由于试验所用的泥灰质岩石较之灰岩对水更为敏感。图2为若干次的风干-饱和循环作用后，原本完整的泥质灰岩试样中产生的可见裂纹。

3 碳酸盐岩单轴抗压强度预测的神经网络方法

自20世纪40年代以来，人类迄今已开发了几十种甚至上百种不同类别的人工神经网络模型，它所具有的非线性映射、学习分类和实时优化等基本特征使其能够解决一些用传统方法难以处理的问题[11-12]。正因为神经网络能学习和存贮大量的输入-输出模式映射关系，而无需事前揭示描述这种映射关系的数学方程，它对于岩石单轴抗压强度这类影响因素较多、且各因素对其影响机制复杂的问题具有极佳的适用性。据此，笔者将采用BP神经网络模型的方法对碳酸盐岩单轴抗压强度进行预测。

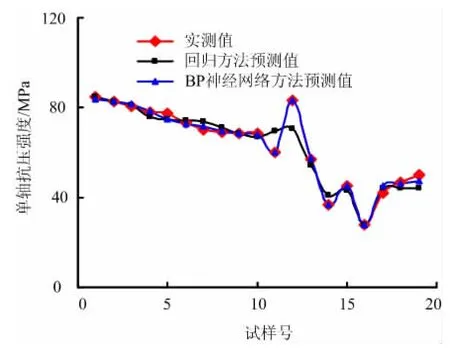
图1 试样单轴抗压强度实测值和预测值关系曲线Fig.1 Relationship curves of measured and predicted values of the uniaxial compressive strength of carbonate samples

图2 风干-饱和循环作用下泥质灰岩中产生的可见裂纹Fig.2 Visible cracks in the argillaceous limestone due to cyclic drying-wetting effect

BP（back propagation）网络是一种按误差逆向传播算法训练的多层前馈网络，是目前应用最广泛的神经网络模型之一。它的学习规则是使用最速下降法，通过逆向传播来不断调整网络的权值和阈值，使网络的误差平方和最小。

在使用神经网络的方法对研究对象进行预测的过程中，所采用预测基本指标的具体数值固然可以作为参数输入神经网络中，同时对于一些描述性的因素（如地质描述中的颗粒形状）、甚至一些人为的因素（如施工方法、管理水平等）也可做为变量输入，此时只需遵循一定的导入规则，把这些抽象的信息变成系统可以辨认的信息即可[13]。因此，对于岩石单轴抗压强度的预测而言，除了一些数量化的物理指标之外，试样的含水状态（天然、烘干、饱和）也完全可以作为参与预测的基本指标，这也是前人采用神经网络方法预测岩石强度所未考虑的。本次研究在使用BP神经网络方法进行数据输入、训练和输出时，对试样的不同含水状态赋以不同数值加以区分辨认，即将天然、烘干、饱和状态下试样的含水条件参数分别赋以3、2、1以进行神经网络分析和预测。

据此，以矿物组成（碳酸钙和基质质量分数）、密度、纵波波速和含水状态为5个输入层节点，以试样的单轴抗压强度为单个输出层节点，根据表1中试样的物理指标参数、含水状态以及实测单轴抗压强度值，经反复试算，当隐层采用单层四节点时，只需运算约27000步，均方差MSE即收敛到0.001的阈值。BP神经网络方法的预测结果见表1，试样单轴抗压强度实测值与本方法预测值的关系曲线见图1。可见，神经网络方法对碳酸盐岩单轴抗压强度的预测也具有较好的适用性，且较之回归方法更为可靠，预测误差更小。

4 所选用预测基本指标与岩石强度的灰色关联分析

一般情况下，研究对象都具有某种不确定性，其构成的因素各式各样且形式较多，灰色理论是研究对象不确定性的一种较为有效方法。在系统发展过程中，若两个因素变化的趋势具有一致性，即同步变化程度较高，即可谓二者关联程度较高；反之，则较低[14]。据此，笔者将采用灰色关联分析法来研究所采用预测基本指标与岩石单轴抗压强度序列之间关联程度，以验证所选指标的合理性。具体实施步骤如下：

1）确定参考序列和比较序列。反映系统行为特征的数据序列，称为参考序列；影响系统行为的因素组成的数据序列，称比较序列。本研究以岩石的单轴抗压强度为参考序列，其矿物组成（碳酸钙和基质含量）、密度、纵波波速和含水状态5项基本指标为比较序列，同时对试样的不同含水状态以不同的数值表示以进行量化分析，即将天然、烘干、饱和状态下试样的含水条件参数分别赋以3、2、1以进行灰色关联分析计算。

2）对数据做均值化处理，使其无量纲化：

其中：Xi（k）为参考序列；X′i（k）为均值化处理后的参考序列，i＝0，1，2，…，m，代表参与计算的数据序列；k＝1，2，3，…，n，代表参与计算的数据样本。无量纲化处理后的数据序列见表2。

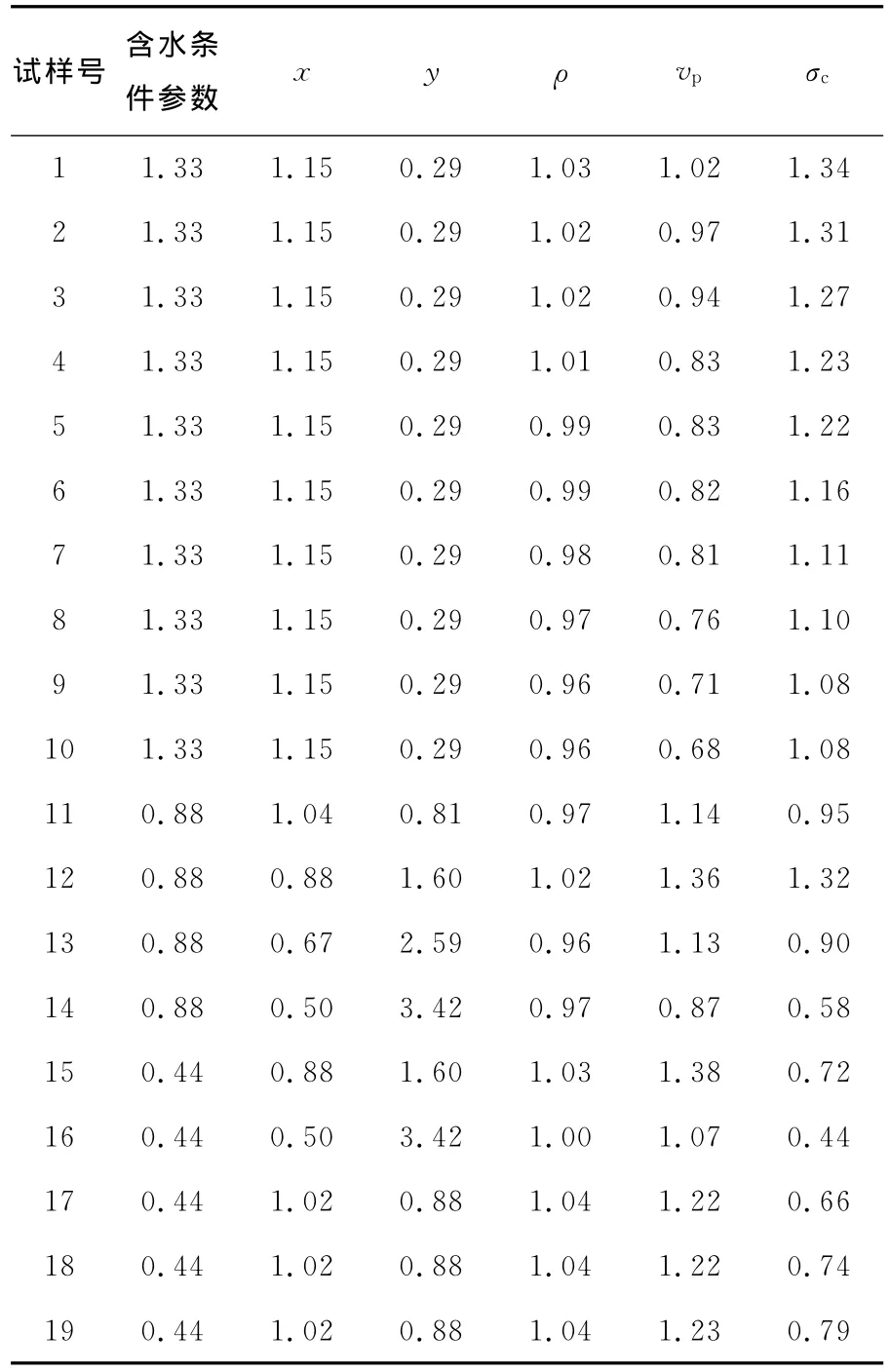
表2 比较序列和参考序列的无量纲化值Table2 Dimensionless values of comparison sequences and reference sequence

3）求参考序列与比较序列的绝对差Δi（k）：

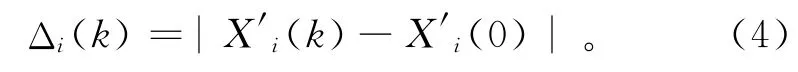
X′i（0）为均值化处理后的比较序列。

4）计算两极最大差Δmax与最小差Δmin：

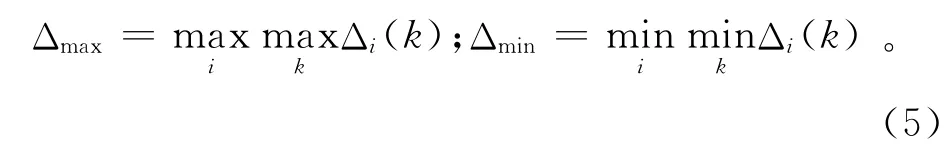
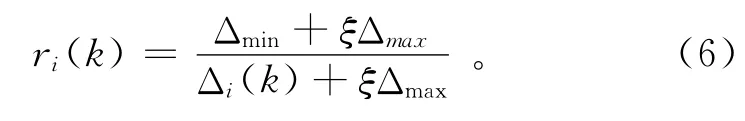
5）计算关联系数ri（k）：ξ为分辨系数，其作用是提高关联系数之间的差异显著性，ξ∈（0，1），一般取ξ＝0.5时即具有较大的分辨率。关联系数ri（k）反映了不同序列在同一点与参考序列的相似程度。

6）求得关联度R（i）：

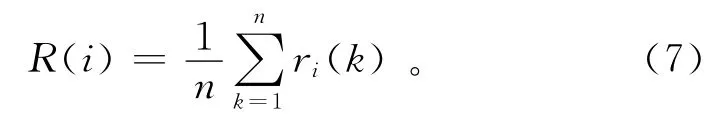
关联度R（i）即反映了比较序列Xi对参考序列X0的相似程度。

7）计算各评价因素的权重Wi：

按以上步骤计算获得各指标的权重见表3。

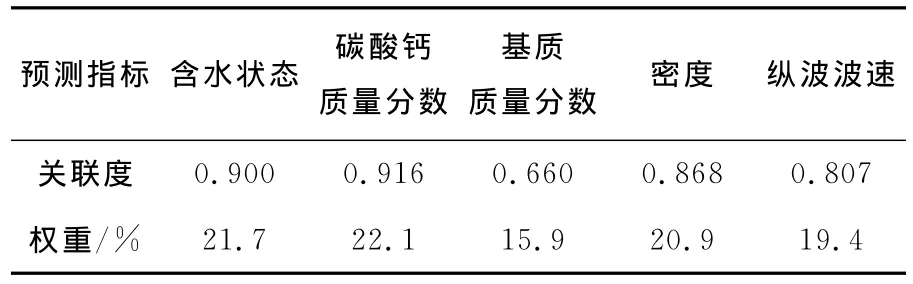
表3 预测指标权重表Table3 Weight of prediction factor

由计算结果可见，本研究所选基本指标对碳酸盐岩单轴抗压强度的贡献率比较接近，即每个指标都对岩石强度具有重要影响。其中碳酸钙质量分数所占权重相对较大，为22.1%，而基质质量分数所占权重相对较小，为15.9%。

根据这5个基本指标的贡献率，可对各个试样进行综合评价，将评价值作为岩石强度的参照。样本综合评价值V的计算式为

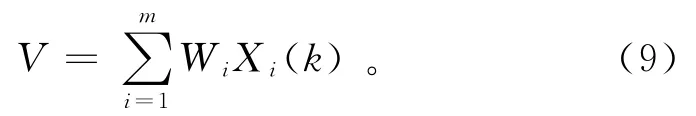
式中：Xi（k）为样本某评价指标的具体数值；Wi为对应指标的权重。

由式（9）计算所得表1中各样本的综合评价值曲线如图3。与图1对比可知，试样的综合评价值与其单轴抗压强度值具有几近一致变化趋势。其中，试样1和试样12综合评价值相对较高，而实际上它们强度相近，且值相对较大（分别为84.5MPa和83.1MPa）；试样16综合评价值最低，而实际上其强度为最小值（28.1MPa）。

灰色关联分析结果说明，本研究中5个预测基本指标的选择较为合理，它们的组合能够较好地反映碳酸盐岩的单轴抗压强度。因此，笔者基于上述指标进行的单轴抗压强度预测研究是合理的。

由以上分析结果可以看出，对同一块碳酸盐岩而言，随着岩溶风化作用的进行，其碳酸钙含量不断减少，黏土矿物含量不断增多，其整体密度也会降低，波速值也将减小，因此其综合评价值就会变低，强度不断弱化，如试样1-10，以及试样11、13、14就充分反映了这一规律。而对于两块不同的碳酸盐岩来说，由于形成条件不同，其强度值将是上述指标的综合反映。如试样11和12，虽然前者碳酸钙含量相对更高，黏土矿物含量相对更少；但后者更为致密，即其密度更高、波速值更大，其反映出来的综合评价值更高，表现出的强度也更大。

图3 试样的综合评价值曲线Fig.3 Curve of comprehensive evaluation values of samples

5 关于预测基本指标的讨论

岩石强度是岩石物质性、结构性、赋存环境状态的宏观综合表现，它与这些因素之间没有明确的力学关系，笔者在综合考虑岩石地质本质性的基础上，根据已有数据采用回归和神经网络的方法来研究碳酸盐岩单轴抗压强度与其矿物组成、密度、纵波波速和含水状态之间的关系。

由于试验条件的限制和出于方便应用的考虑，本研究对于岩石地质本质性的考虑还不能做到绝对地全面：对于岩石的物质性，上文已提到碳酸盐岩矿物组成在一定程度上比较多样，如需充分考虑各组分对其强度的影响，则应额外计入其他物质成分的比例、并分配相应的强度贡献系数；其次对于岩石的结构性，本方法只适用于无层理等结构面发育的完整试样，当试样中存在肉眼不可见的微裂隙时，其方位特征对波速值的影响较大，尤其当试样存在近轴向的微裂隙时，其预测结果将可能出现较大的误差；而对于岩石的赋存状态，以相同物质组成、结构和试验方法、不同初始应力状态的碳酸盐岩为例，其在室内力学试验中由于不同的应力历史将必然会表现出不同的强度特征。

在这种情况下，进一步完善本预测方法将可以得出更多有益的结果，如通过充分考虑岩石的组成成分，以将本预测方法推广到其他多相物质组成的均质岩石；通过考虑试样中微层理等结构面方位的影响，可在公式中增加表征其各向异性的系数以进行修正；通过建立可溶盐岩溶蚀过程中孔隙度变化与其波速、密度、组成成分变化的规律，则可以推导出这类岩石在溶蚀作用过程中单轴抗压强度的变化规律，这些内容将在后续的研究中开展。

6 结论

1）在考虑岩石地质本质性的基础上，应首先合理确定影响岩石力学性质的基本指标。笔者所选碳酸盐岩的单轴抗压强度预测的基本指标是矿物组成、密度、纵波波速和含水状态。

2）笔者采用的回归方法对该类岩石单轴抗压强度预测的最大误差为15.3%，BP神经网络方法预测的最大误差为8.5%。由于神经网络所具有非线性映射和实时优化等特征，因而该方法较之回归方法具有更高的精度和更强的容错能力。其中预测误差出现的原因为碳酸盐岩物质组成复杂，笔者所选预测基本指标只是实际情况的简化；同时泥灰质岩石所具有的膨胀性也导致其经含水状态变化后的实测和预测结果具有一定的差异。

3）灰色关联分析表明，试样的综合评价值和试样实测单轴抗压强度具有一致的变化规律，因此笔者所确定的用于预测的基本指标对岩石单轴抗压强度是具有重要影响的，其组合是合理的。

（References）：

[1]邓华锋，李建林，邓成进，等.岩石力学试验中试样选择和抗压强度预测方法研究[J].岩土力学，2011，32（11）：3399-3403.Deng Huafeng，Li Jianlin，Deng Chengjin，et al.Analysis of Sampling in Rock Mechanics Test and Compressive Strength Prediction Methods[J].Rock and Soil Mechanics，2011，32（11）：3399-3403.

[2]Heidari M，Khanlari G R，Mehdi Torabi Kaveh，et al.Predicting the Uniaxial Compressive and Tensile Strengths of Gypsum Rock by Point Load Testing[J].Rock Mechanics and Rock Engineering，2012，45（2）：265-273.

[3]Sarkar Kripamoy，Tiwary Avyaktanand，Singh T N，et al.Estimation of Strength Parameters of Rock Using Artificial Neural Networks[J].Bulletin of Engineering Geology and the Environment，2010，69（4）：599-606.

[4]杨文甫，佴磊，祝玉学，等.预测岩石单轴抗压强度的神经网络方法[J].水文地质工程地质，2003（6）：52-54.Yang Wenfu，Nai Lei，Zhu Yuxue，et al.Method of Neural Network for Predict Uniaxial Compressive Strength of Rock[J].Hydrogeology and Engineering Geology，2003（6）：52-54.

[5]Dehghan S，Sattari Gh，Chehreh Chelgani S，et al.Prediction of Uniaxial Compressive Strength and Modulus of Elasticity for Travertine Samples Using Regression and Artificial Neural Networks [J].Mining Science and Technology ，2010，20（1）：41-46.

[6]Zorlu K，Gokceoglu C，Ocakoglu F，et al.Prediction of Uniaxial Compressive Strength of Sandstones Using Petrography-Based Models[J].Engineering Geology，2008，96（3／4）：141-158.

[7]Tawadrous A S，Degagne D，Pierce M，et al.Prediction of Uniaxial Compression PFC3DModel Micro-Properties Using Artificial Neural Networks[J].International Journal for Numerical and Analytical Methods in Geomechanics，2009，33（18）：1953-1962.

[8]王新，丁秀丽.含石量对土石混合体力学特性影响的数值试验[J].水运工程，2010（10）：93-99.Wang Xin，Ding Xiuli.Numerical Tests on Impact of Stone Content to Mechanical Parameters of Soil-Rock Mixture[J].Port and Waterway Engineering，2010（10）：93-99.

[9]王思敬.论岩石的地质本质性及其岩石力学演绎[J].岩石力学与工程学报，2009，28（3）：433-450.Wang Sijing.Geological Nature of Rock and Its Deduction for Rock Mechanics[J].Chinese Journal of Rock Mechanics and Engineering，2009，28（3）：433-450.

[10]张加桂.三峡地区泥灰质岩石在岩溶和风化过程中力学性质的变化[J].岩石力学与工程学报，2004，23（7）：1073-1077.Zhang Jiagui.Variation of Mchanical Property of Marlite in Process of Karstification and Weathering in Three Gorges Region[J].Chinese Journal of Rock Mechanics and Engineering，2004，23（7）：1073-1077.

[11]高浪，谢康和.人工神经网络在岩土工程中的应用[J].土木工程学报，2002，35（4）：77-81.Gao Lang，Xie Kanghe.Application of Artificial Neural Networks to Geotechnical Engineering[J].China Civil Engineering Journal，2002，35（4）：77-81.

[12]刘兴远.神经网络理论在土木工程应用中的几点认识[J].岩土工程学报，2003，25（4）：514-516.Liu Xingyuan.Discussion on Neural Network Application in Civil Engineering[J].Chinese Journal of Geotechnical Engineering，2003，25（4）：514-516.

[13]张清，宋家蓉.利用神经元网络预测岩石或岩石工程的力学性态[J].岩石力学与工程学报，1992，11（1）：35-43.Zhang Qing，Song Jiarong.Predicting Mechanical Behaviors of Rock or Rock Engineering by Neural Network[J].Chinese Journal of Rock Mechanics and Engineering，1992，11（1）：35-43.

[14]邓聚龙.灰色系统理论教程[M].武汉：华中理工大学出版社，1990.Deng Julong.Grey System Theory Teaching[M].Wuhan：Huazhong University of Science and Technology Press，1990.