基于同态滤波的图像照度补偿算法研究

周龙杰

（汕头大学工学院，广东 汕头515063）

图像细节受光照影响较为明显，部分图像细节会由于光照不均匀而难以看清。为了消除照度不足给图像带来的影响，可以利用基于同态滤波的光照反射模型，在不损失图像细节的前提下进行照度补偿。作为一种图像预处理方法，同态滤波技术结合灰度变换和频率过滤方法，通过增强对比度和压缩灰度范围改善图像细节。目前，该技术在图像对比度增强、照度补偿、灰度修正和图像恢复中得到广泛应用。本文介绍了同态滤波原理，结合传统巴特沃斯高通滤波方法，提出一种新的同态滤波函数，并选取滤波参数，经过实验及分析，得出结论。

1 图像同态滤波原理

图像同态滤波原理是基于将图像看成由反射光和照射光的乘积，对一副图像进行傅里叶变换，可将乘积关系转化为卷积关系进行处理。图像同态滤波可以很好地解决光照问题，取得良好的图像增强效果［1］。

若用Iσ（x，y）表示图像的入射分量，Iτ（x，y）表示图像的反射分量，那么数字图像I（x，y）可表示为

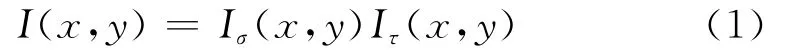
Iσ（x，y）代表图像内容，属于频域内的高频分量，随着图像细节的不同作快速变化，对应图像中物体的边缘；Iτ（x，y）的变化比较缓慢，属于频域内的低频分量。对式（1）两边分别取对数，将两个相乘分量转化为两个相加分量，即

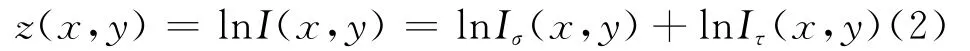
对两边求傅里叶变换，得到

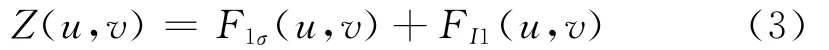
通过式（3）在频域中将图像入射分量和反射分量分离开。从它们自身的空间变化特征来看，低频部分为入射分量频谱，高频部分为反射分量频谱。典型同态滤波法为：对原图进行对数变换和快速傅里叶变换，分离出图像的高频分量和低频分量，然后选择适合不同需要的传递函数改良照度不均的图像，最后对经过频域处理的图像进行快速傅里叶逆变换和指数变换，最终得到经过预处理的图像。对Z（u，v）采用滤波传递函数 H（u，v）进行处理，代入式（3）可得

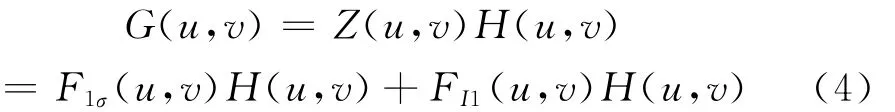
对式（4）进行快速傅里叶逆变换，并令J’σ（x，y）＝F－1（F1σ（u，v）H（u，v）），J’1（x，y）＝F－1（FI1（u，v）H（u，v）），可得

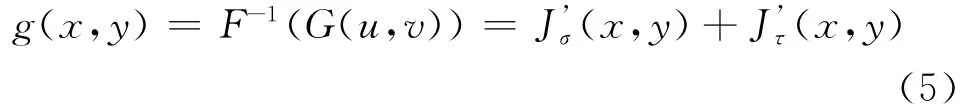
对式（5）进行指数变换，得到最终经过照度补偿的图像I’（x，y），表示为

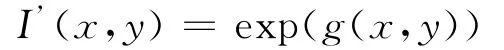
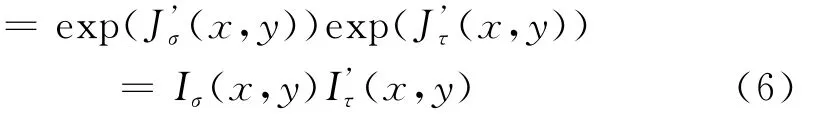
同态滤波的关键在于传递函数H（u，v）的确定，滤波器函数对图像高频部分和低频部分的响应各不相同，通过压缩像素灰度范围和增强图像对比度，从而达到照度补偿的效果［3］。

2 同态滤波函数确定及参数选取

传统巴特沃斯高通滤波器的传递函数为

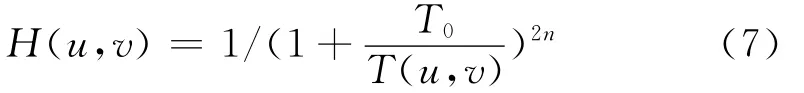
式中，T（u，v）表示任意频率（u，v）和滤波器中心（u0，v0）之间的距离，T0表示截止频率。为了达到压缩灰度动态范围，并取得进一步改善图像增强效果的目的，对传统巴特沃斯高通滤波器加以改进。

设Eh代表高频增益，El代表低频增益，当Eh＞1，El＞1时，滤波函数可以在增强反射分量的同时抑制入射分量，从而达到增强图像对比度和压缩像素动态范围的目的。对式（7）修改如下

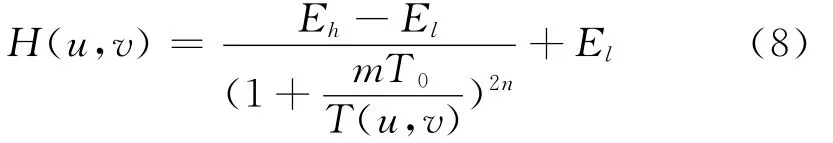
式中，m为锐化系数，目的是对滤波器的斜面锐化加以修正［2］。m值的选取必须在El和Eh之间，T0的选择必须在进行大量实际比较的基础上，充分考虑反射函数和照度函数加以确定。这种选择方式既浪费时间和精力，经实践证明取得的效果也不好，因此有必要通过选取适当滤波参数，设计合适的同态滤波器模型来克服这个困难。

在图像频域，不同频率分量的组合代表着图像的信息。对于一幅X×Y图像f（x，y），对其进行离散傅里叶变换可得

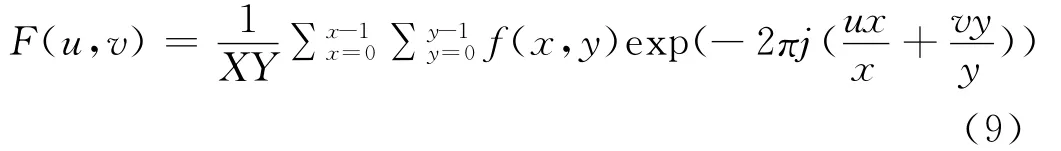
式中，u＝0，1，2，……，X－1；v＝0，1，2，……，Y－1。F（u，v）的实部为Re（u，v），虚部为Im（u，v），那么其频谱可由下式表示

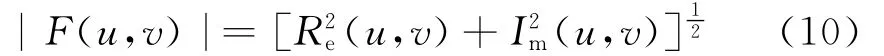
由式（10）可知，T0可通过以下方法计算得到

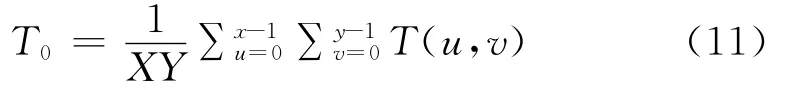
同理，对巴特沃斯低通滤波器进行修改，加入高频、低频增益以及锐化系数，结合巴特沃斯高通滤波器，可得到巴特沃斯带阻滤波器，其传递函数表示为

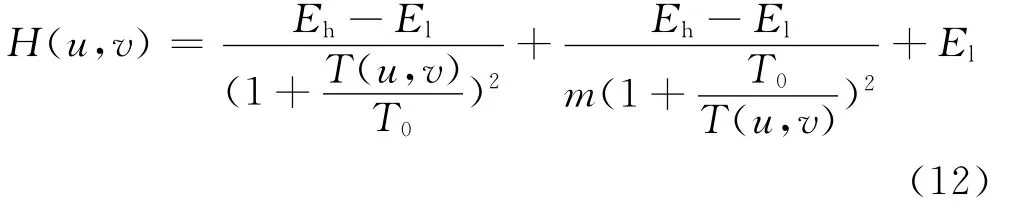
3 实验结果及分析

基于Matlab软件，分别采用巴特沃斯同态高通滤波器和改进的巴特沃斯同态带阻滤波器对lena图像进行照度补偿，效果如图1所示。同态滤波器的参数设置如表1所示。

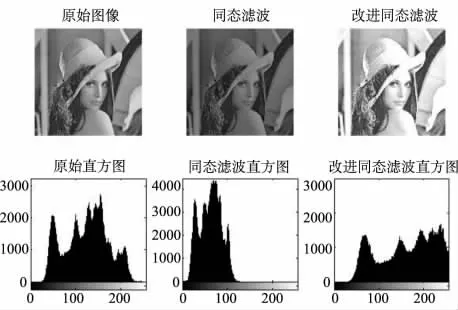
图1 滤波效果对比

表1 同态滤波器参数

从图1可以看出，两种滤波器都对图像起到了照度补偿的作用。很明显，虽然在具有相同低频增益的条件下，两者都可以清楚地显示图像细节，但经过巴特沃斯高通滤波的图像反而使原图中较亮的部分变暗；而对于经过巴特沃斯带阻滤波的图像来说，不仅起到了照度补偿的作用，而且通过观察两者的直方图可以发现，经过巴特沃斯带阻滤波的图像更好地抑制了图像噪声，大大增强了图像对比度，效果更为理想。

4 结 论

通过以上对实验结果的比较和分析可知，改进后的巴特沃斯同态滤波器对于图像的照度补偿效果更为理想，同时也大大增强了图像对比度。对于照度不均的图像来说，该种算法的图像增强效果异常明显，可以在突出图像暗处细节的同时很好地抑制高亮部分。

［1］ Richar d J Radke，Srinivas Andra，Omar Al－Kofahi，Badrinath Roysam.Image change detection algorith ms：a systematic survey［J］.IEEE TRANSACTIONS ON I MAGE PROCESSING，2005，14（3）：294－307.

［2］ 陈春宁，王延杰.在频域中利用同态滤波增强图像对比度［J］.微计算机信息，2007，23（6）：264－266.

［3］ 张新明，沈兰荪.基于小波的同态滤波器用对比度增强［J］.电子学报，2001，29（4）：531－533.

［4］ 黄剑玲.利用MATLAB进行数字图像的分析和处理［J］.计算机与现代化，2000，（6）：104－107.