基于压缩感知的交通监控视频目标检测算法
2013-09-24李芬兰彭卓韬庄哲民
李芬兰,彭卓韬,庄哲民
(汕头大学工学院电子系,广东 汕头 515063)
0 引言
目前,我国高速公路视频监控系统主要有以下两方面不足,一方面,随着高清化节奏的加快,人们对数据清晰、详细度要求的增大,从而要求的信息量和带宽也越来越大,导致费用十分昂贵.另一方面,目前普通高清IP摄像机的工作方式是高采样到高清视频数据后再进行压缩,经过大量的运算后抛弃掉大部分冗余的数据,这就造成采样资源极大浪费和采样端设备器械的造价成本大幅上升.近几年来压缩感知(Compressed Sensing,简称CS)[1]理论的出现恰好提供了解决这两大难题的思路,它指出,只要信号是可压缩的或在某个变换域是稀疏的,就可以用变换空间描述信号,通过直接采集得到少数"精挑细选"的线性观测数据,通过求解一个优化问题就可以从这些少量的压缩观测值以高概率重构出原信号,所以,它可降低对高清视频数据的采集成本和传输带宽,从而减少网络费用,具有广泛的应用前景.
传统的压缩感知重构算法运用的是基跟踪技术,重构出的信号误差较大.贝叶斯压缩感知是基于贝叶斯推论,利用随机变量之间依赖关系,将数据有效地转化为知识,再利用这些知识进行推理,来求解不确定性问题的一种重构方法,它提供更为精确的估计或者减少CS观测量的途经.文献[2]提出了基于相关向量机的贝叶斯CS框架估计信号.文献[3]针对临时互相关构建了分块稀疏的贝叶斯学习框架,把高维测量向量转换到低维测量向量.文献[4]构建一个分层的贝叶斯模型,使用马尔可夫蒙特卡罗采样进行有效的估计,提出了贝叶斯树结构小波压缩感知(tree-structured wavelet compressive sensing,简称TSW-CS)重构算法,该算法在图像重构的效果比目前很多算法都要好.
国内外专家在背景分割上都做了很多研究,总结常见的背景分割方法有四类:背景差分法、帧间差分法、光流法和分类法[5-10].背景差分方法由它实现最简单,并且能够完整地分割出运动目标,适合交通车辆摄像头的终端节点处理.文献[11]描述了一种直接重构压缩感知的背景差分图像的方法,从理论分析和实验结果验证了它的可行性,但重构的背景差分图效果不够理想.本文结合压缩感知、小波分析和马尔可夫链蒙特卡洛的思想,提出一种新颖的基于小波分析的贝叶斯压缩感知背景分割的目标检测算法.这种方法不同于传统的目标检测算法,它可以减少终端节点的信息储存和传输量同时有较好的目标检测精度.文章首先针对视频图像信号的特点,采用了Daubechies小波基进行信号稀疏,以对比方法选取了更为合适的哈达玛测量矩阵,然后提出在部分时间均衡的自适应背景模型,再结合背景模型和TSW-CS算法重构出目标.
1 研究思路和基本步骤
1.1 算法架构
以往的视频监控为了减少传输数据量,都要把拍摄下来的录像进行压缩编码,复杂的压缩编码需要较大的运算量,这时对前端设备的要求很高,费用也较昂贵.本文运用压缩感知方法,在前端只需进行简单的观测即可得到压缩的信号.在前端可以使用智能DSP芯片对监控视频进行智能分析并完成压缩感知采样,然后将压缩视频流传输到后端系统平台,系统平台由大型高速计算机和监控中心组成,再对视频流进行重构得出目标图像并分析目标的细节来获取有关的信息.
1.2 算法流程
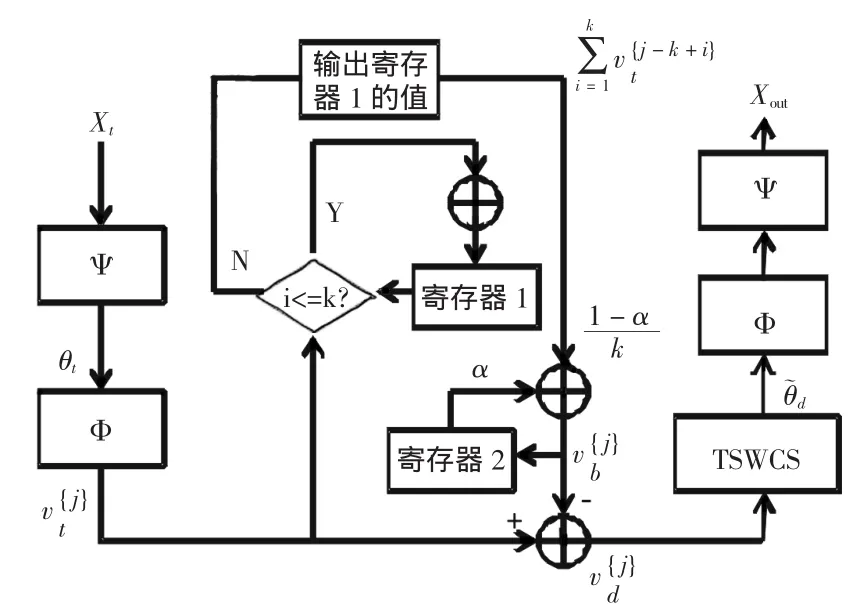
算法的基本步骤如下:先终端节点的视频摄像头获取视频信号,对视频信号进行小波基稀疏表示,然后使用哈达玛矩阵进行观测得到网络传输带加性噪声的压缩信号,在接收端进行信息处理,使用结合背景差分法的TSW-CS重构算法估计背景分割后的图片,最后使用形态学(或膨胀运算)的得到检测目标,具体如图1所示.
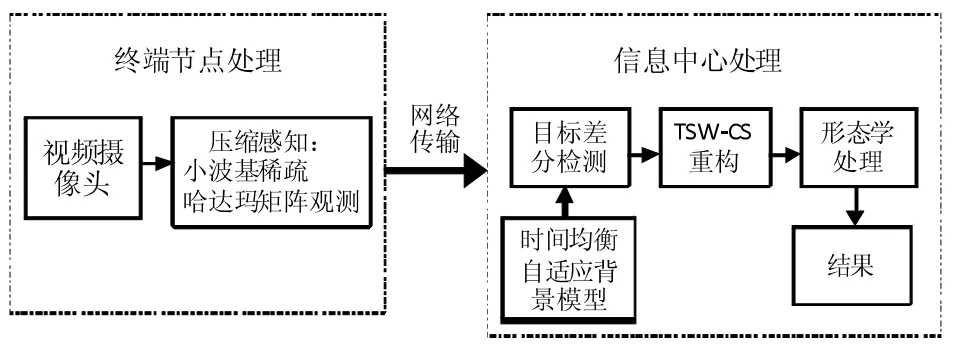
图1 本文目标检测系统的流程图
2 基于压缩感知的背景分割
2.1 稀疏表示
假设我们有一个大小为N1XN2的图像X,以每一顺序连接起来向量化为一个NX1(N=N1N2)列向量x.图像向量x的第n个元素记作x(n),其中n=1,…,N.再假设正交基Ψ=[ψ1,…,ψN],其稀疏度为K,则x表示如下:

其中θ(n)是第n个向量基ψn=(ψn:NX1)的系数,并且这K个非零系数的下标用nl表示,K< 在普通的数据采集系统中(例如数码摄像机),首先采集图像x的全部N个像素点采样,然后进行变换编码,计算出全部的变换系数θ=ΨTx,找出稀疏度为K的K个最大系数并将N-K个较小的系数全部丢掉,将这K个最大系数的值以及它们所在的位置用来编码.这样先采样后编码的框架本身存在采样量过多,并且只需要K个较大系数,但要将全部的变换系数计算出来和系数值编码都无疑引起额外的开销.在CS框架中,取消采集全部N个像素点的中间过程,直接以压缩的方式采集信号,即采用另外一个与正交基Ψ不相关的观测矩阵Φ:MXN,(M 可见压缩感知的采样量只要M,这样的观测过程是非自适应的,在很大程度上依靠观测矩阵的选取.通常随机观测矩阵因为它提供了广泛的观测矩阵与稀疏矩阵不相干对,给重构提供了条件,往往两者不相关度越大,重构的效果会越好.目前随机矩阵在观测矩阵中应用很广泛,例如高斯随机矩阵、随机正交矩阵、随机贝努利矩阵等,本文采用部分哈达玛(Hadamard)观测矩阵,是由于哈达玛矩阵为正交方阵,它的任意两行(或两列)都是正交的这一特点,在随机矩阵中的不相关性较好. 部分哈达玛矩阵的构造方式是:生成大小为NXN的哈达玛矩阵,然后在生成矩阵中随机地选取M行向量,构成一个MXN的矩阵. 则称H为n阶哈达玛矩阵. 五种测量矩阵在对同一帧情况下,三摩托车监控视频的检测,统计出各自的信噪比(SNR)如下表1所示. 表1 各种不同测量矩阵的重构信噪比对比表 表1可见在稀疏度一样时,哈达玛测量矩阵在5种测量矩阵中重构后的信噪比(SNR)是最高的,更能准确重构. 在隐式马尔可夫树模型中,小波系数描述成一个由两个零均值、不同方差的高斯分布所组成.这里的两个高斯分布分别表示两种隐式状态,第一种状态为高状态,相应是θm,描述为大方差的高斯分布,另外一种状态为低状态,相应是θc,描述为小方差的高斯分布.同时马尔科夫树模型的概率转换矩阵P,为2X2矩阵,其中P(i,j)表示子系数在状态j,相应的父系数在状态i;i=1和j=1表示低状态,i=2和j=2表示高状态,即(初始状态分布为[1-πr,πr]) 对于计算机视觉来说,自然图像在小波域内是可以被稀疏表示的.根据压缩感知理论,CS观测量v=Φx=ΦΨθ,其中Φ是一个MXN维矩阵(M 根据之前隐式马尔可夫模型的描述,θc能够建模为一个零均值、方差σ2e的高斯分布.当我们假设压缩感知的观测量中包含了加性噪声,该噪声n0为零均值,方差为的高斯噪声,则观测量为,其中nc+n0可化简为一个零均值,方差为σ2的高斯分布.在CS重构中,就是通过重构算法,估计出θk在向量序列θ中的值和位置. 利用贝叶斯回归和因子模型中的峰平(spike and slab)先验知识[13,14],我们对第i个小波系数θ服从其中δ0是接近0的值,πi是混合加权值.因为每一个观测量都是整幅图像的一个随机投影,所以观测值满足常数方差的独立同分布的高斯分布,即再采用小波估计模型建立.根据以上结论,参考文献[4]建立贝叶斯树结构小波压缩感知模型(TSW-CS)描述为: 其中 其中混合加权πi,精度参数αi和未知噪声精度αn,θs,j表示在尺度s下的第i个小波系数,i=1,…,Ns(Ns是在尺度s下小波系数的全部个数),πs,i是相关混合加权,θpa(s,)j表示θs,i的父系数,L为分解等级的个数.在(5)式里,带有零值的父级在尺度下s所有系数分享一个混合加权π0s,带有非零的父级在尺度s下稀疏分享一个混合加权π1s.噪声精度αn和非零系数精度αs都描述成Gamma先验分布,其中a0=b0=c0=d0=1X 10-6,而他们的后验概率则有数据里推导出来.混合加权值πsc,πr,π0s和π1s都描述成Beta分布,其中,esc=(1-δ)Nsc,fsc=δNsc,Nsc为尺度系数的个数,er0=0.9Ns,fr0=0.1Ns,,其中s=2,…,L. 设背景图、测试图和差分图为xb,xt和xd,差分图是由测试图与背景图相减所得.差分图的支撑,它提供了检测目标的位置和外形.假设xb和xt是自然图像,采用小波基稀疏的条件下使用K个变换系数实现较准确的近似,那么差分图像xd的支撑集P=Sd的像素且P< 在N维重构维数下,xb,xt和xd的观测量M的个数[12]可确定为Mscene=Mb=Mt≈和其中α为一个较小的常正数.为了比较Md与Mscene的大小,先假设Md 公式(6)可以化简为 重构前景我们采用TSW-CS算法[4],该算法是基于Gibbs采样的马尔科夫蒙特卡罗(MCMC)算法[16]来计算后验知识.这种MCMC算法的一个显著特点是每步迭代都用条件分布(这些分布是通过将目标分布限制在一定的子空间产生的)来构建马尔可夫链并最终收敛于平稳分布.算法的具体描述如下: 1)假设随机变量先验概率: 2)在每次MCMC迭代过程中,由式(5)和(7)得重构小波系数的条件先验分布为: 其中θs,j是N维向量θ的第j元素,表示θ(j),则,其中 4)经过k次MCMC迭代后,由蒙特卡罗方法得到重构后小波系数的近似形式θ˜=,得检测后的目标图像. 由于光照、相机的抖动、阴影的变化都会使背景发生变化,为了提高算法的鲁棒性和准确性,本文提出了局部时间均衡的自适应背景模型,学习公式: k表示步长,步长越大对于短时间剧烈运动的分辨能力越差,但相反可以减少低速运动物体的干扰,更准确地识别出它,提高鲁棒性,α表示模型的学习速度,其倒数表示衰减过程的时间常数,一般是经验值.该模型在每隔k帧更新一次,将该时刻的前k帧的图像进行均衡从而获得.其中初始背景v{b1}为第一帧v{t 1} 图2 动态目标识别检测系统的流程图 当视频通过摄像头采集后,以一帧一帧的形式进入动态目标识别检测系Z统中,系统会根据目标的移动情况自动更新背景,使得背景模型适应环境的变化. 为了验证算法的有效性,对分辨率为128X128像素的多个目标真实场景的交通监控录像进行了测试,其中包含树荫、树叶、路面等复杂背景的干扰,以及各种不同车辆目标的新生、消失等跟踪场景,摄像头每秒采集25帧. 实验测试内容:1)为了比较在本文检测系统下对室外交通监控视频进行检测,获得不同帧下各种车辆的测试结果,并检测出目标个数,实验参数α=0.5,步长k=7,观测比M/N=10%.2)不同观测比M/N下进行检测.3)TSW-CS重构算法与其他常用的重构算法进行检测比较,对比信噪比、相对重构误差和重构时间. 图3为实验(1)的大马路视频的检测结果,第一行图片为原跟踪画面(原始视频信号),第二行为常规背景差分法得到前景图像,再进行压缩感知并使用TSW-CS重构,第三行为本算法相应检测结果,第四行为形态学处理后的检测结果和检测目标个数;图中白色图案为背景分割后的目标图像.由图可见,先进行背景差分再压缩感知的话,由于重构算法在低观测率下会出现较大的失真,对比第二、三行图像,本算法的检测效果有较大的提升.在图3(a)中,可以看到马路上有七辆汽车,从马路上方往下行驶,我们的算法都能检测出来,只是最顶部的三辆汽车行驶比较靠近,在形态学处理后会误判为同一目标.图3(b)有六辆汽车,虽然画面顶部的几辆汽车目标较小,但是本算法也能准确检测出来.图3(c)的形态学结果中,顶部出现两个目标是由于斑马线上行人的走动所致,对于靠近摄像机的两辆汽车都能检测出来.图3(d)的两辆汽车能清楚地检测出来.为了对检测效果有一个定量的分析,我们定义检测率=;统计实验结果,该视频的检测率为94.1%. 图3 不同帧视频下的目标检测效果图 如图4为实验(2)中大马路视频的本算法在观测比M/N为15%,10%,5%下,第235帧视频的检测结果.从图4可以看出,当不适应自适应背景模型,在观测率为10%时目标非常不清晰,背景噪声过大导致检测率下降,而使用自适应背景模型后,检测效果会更良好和清晰,这是由于固定背景不可能完全适应即时视频背景的配对,会在光照或者抖动的影响下降低检测准确度.同时可见,在观测比为10%以上,检测结果都能比较好得重构出原检测目标,观测比为5%时噪声会比较大,可借助滤波提取到检测.另外,本背景模型在步长k为1-3时,能较好地检测高速运动物体,在7-9时,能较好地检测低速运动物体.需要注意的是,步长如果取大了之后,快速运动的物体检测结果会出现拖尾现象,所以要根据实际需要合理选取步长,一般情况α取(0.5~0.7),k取(4~6)为佳. 图4 大马路视频中第235帧的检测结果.第一行为有使用自适应背景模型的结果,第二行为未使用自适应背景模型的结果 图5 五种重构算法在观测比为10%的检测结果对比图 图5 为实验(3)把常规背景差分法与目前常用的5种重构算法和TSW-CS算法的效果对比图,以卡口监控视频的第51帧为例,观测比为10%.可以看出,在观测量比较小的时候,本文TSW-CS算法的信噪比是最高的,而且目标的细节都最为清晰,跟没进行压缩感知的背景差分所检测的目标十分接近,从而在大大减少采样率的前提下,实现了有效的预测跟踪,确保较好的检测准确度.这是由于TSW算法集中更多能量在低尺度分辨上,检测目标一般只要轮廓不需要太多细节,所以需要的是目标的低尺度的小波系数,因此用TSW-CS算法重构更为准确. 图6 各重构算法的信噪比 图7 各重构算法的相对重构误差 图8 各重构算法的重构时间 如图6-8所示TSW-CS重构算法比与OMP、StOMP、GPSR、TVAL3四种算法的重构比较,其中TSW-CS的迭代次数为15,OMP和StOMP的最大迭代次数为50,GPSR和TVAL3的最大迭代次数为100.可见,TSW-CS的信噪比在每个观测量个数下都是最高,更准确地恢复目标的轮廓和有关部分细节.相对重构误差(Relative Reconstruction Error)定义为,其中f代表原图像信号,˜f代表重构信号,由图7可见TSW-CS相对重构误差最小,重构精度最高,从视觉上可以明显看出差异.由图8可见TSW-CS的重构时间属于中等,在N=2000后逐渐少于StOMP,与OMP算法平均相差4秒,重构时间在五种算法里占优.由于TSW-CS的迭代次数固定,所以重构时间相对变化比较平稳,而其他四种算法会由于观测量增加,导致迭代所选原子也增多,错选原子的概率也增加,迭代次数也就会增加,重构时间增长. 本文以压缩感知理论为基础,建立了使用与交通监控视频目标检测的CS框架,以db3小波稀疏为基础,通过哈达玛矩阵进行随机抽取行的方法构建测量矩阵,该方法解决传统的视频编码需要较大的运算量的问题,可以减轻视频采集终端的硬件处理任务,减少网络传输的数据量,将更多的运算转入后端信息处理中心. 结合背景差分思想、TSW-CS重构算法和局部时间均衡自适应背景模型而组成的目标检测系统,对多个车辆目标的几个视频进行检测,从而得到其准确性以及分析误差出现的原因.实验结果表明,本文提出的检测系统能在较高压缩比的情况下提取出前景区域,并较快速地完成信号重构,具有工程可实现性.下一步工作主要集中于重构算法的改进和寻找特定有效的观测矩阵进行观测,得到更好的结果. [1]Donoho D L.Compressed sensing[J].IEEE Transactions on Information Theory,2006,52(4):1289-1306. [2]Ji S H,Xue Y,Carin L.Bayesian compressive sensing[J].IEEE Transactions Signal Processing,2008,56(6):2345-2356. [3]Zhang Z L,Rao B D.Sparse signal recovery with temporally correlated source vectors using sparse bayesian learning[J].IEEE Journal of Selected Topics in Signal Processing,2011,5(5):912-926. [4]He L H,Carin L.Exploiting structure in wavelet-based bayesian compressive sensing[J].IEEE Transactions Signal Processing,2009,56(9):3488-3497. [5]Jain R,Sankar K P,Jawahar C V.Interpolation based tracking for fast object detection in videos[C]//Computer Vision,Pattern Recognition,Image Processing and Graphics(NCVPRIPG),2011 Third National Conference on.IEEE,2011:102-105. [6]朱明旱,罗大庸.基于帧间差分背景模型的运动物体检测与跟踪[J].计算机测量与控制,2006,14(8):1004-1006. [7]Wang P,Shen C H,Barnes N,et al.Fast and robust object detection using asymmetric totally corrective boosting[J].IEEE Digital Object Identifier,2012,23(1):33-46. [8]Ng H F.Automatic thresholding for defect detection[J].Pattern Recognition Letters,2006,27(14):1644-1649. [9]Lin R S,Ross D,Lim J,et al.Adaptive discriminative generative model and its applications[J].Advances in neural information processing systems,2004:17:801-808. [10]Collins R T,Liu Y X,Leordeanu M.Online selection of discriminative tracking features[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,2005,27(10):1631-1643. [11]Cevher V,Sankaranarayanan A,Duarte M F,et al.Compressive sensing for background subtraction[M]//Computer Vision-ECCV 2008.Springer Berlin Heidelberg,2008:155-168. [12]李小波.基于压缩感知的测量矩阵研究[D].北京:北京交通大学,2010:9-21. [13]Carvalho C M,Chang J,Lucas J E.High-dimensional sparse factor modeling:applications in gene expression genomics[J].Journal of American Statistical Association,2008,103(484):1438-1456. [14]Ishwaran H and Rao J S.Spike and slab variable selection:frequentist and bayesian strategies[J].American Statistical Association,2005,33:730-773. [15]Ray S,Mallick B.Functional clustering by bayesian wavelet methods[J].Journal of the Royal Statistical Society.2006,68(2):305-332. [16]Robert C P,Casella G.Monte carlo statistical methods[M].2nd.ed,New York:Springer,2004:56-90.2.2 部分哈达玛观测矩阵

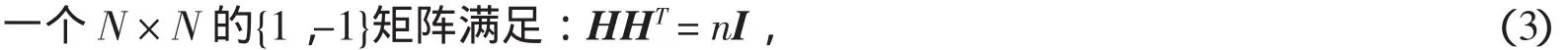
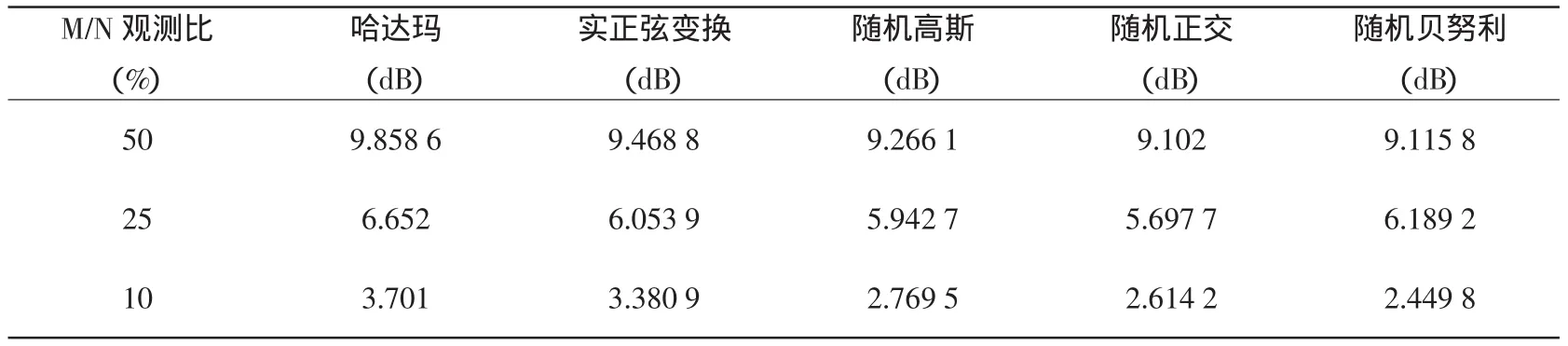
2.3 图像的稀疏表示

2.4 背景差分图像模型
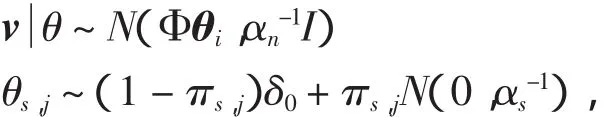
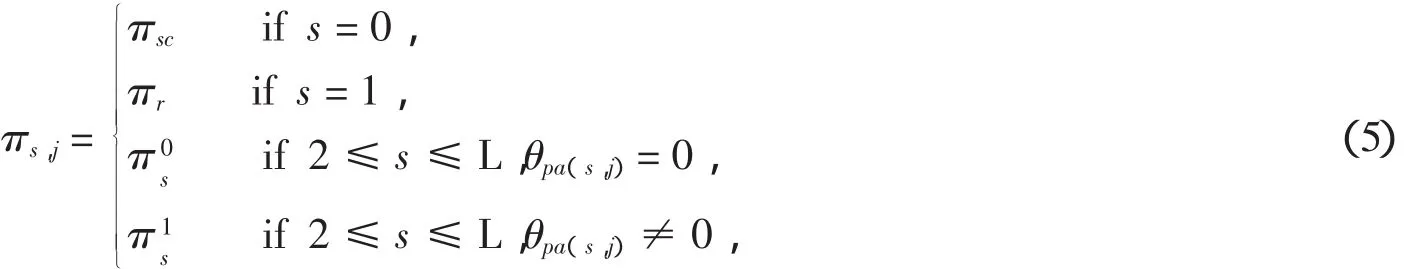
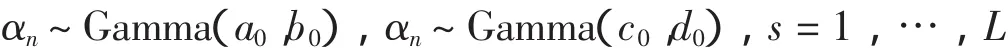
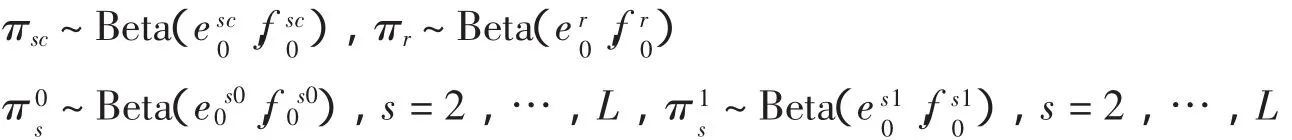
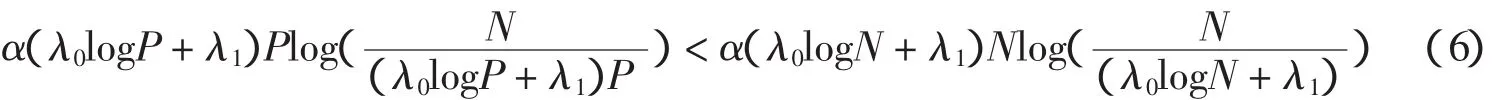
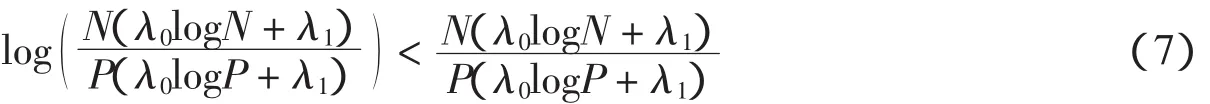
2.5 基于压缩感知的前景重构
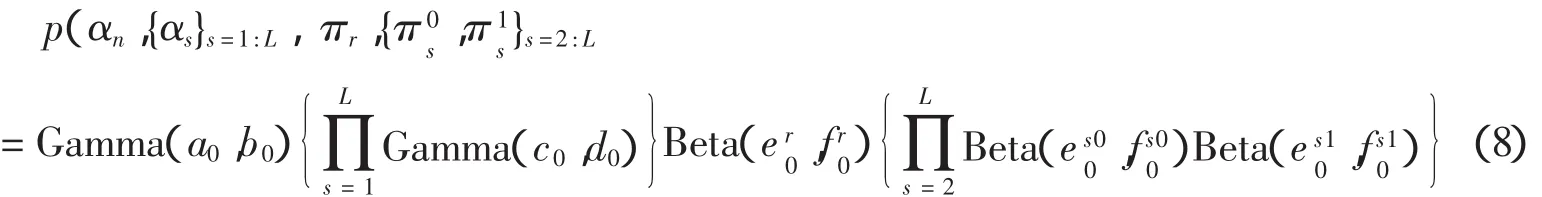
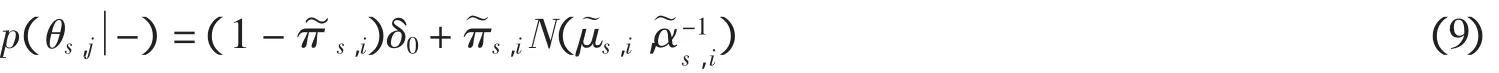
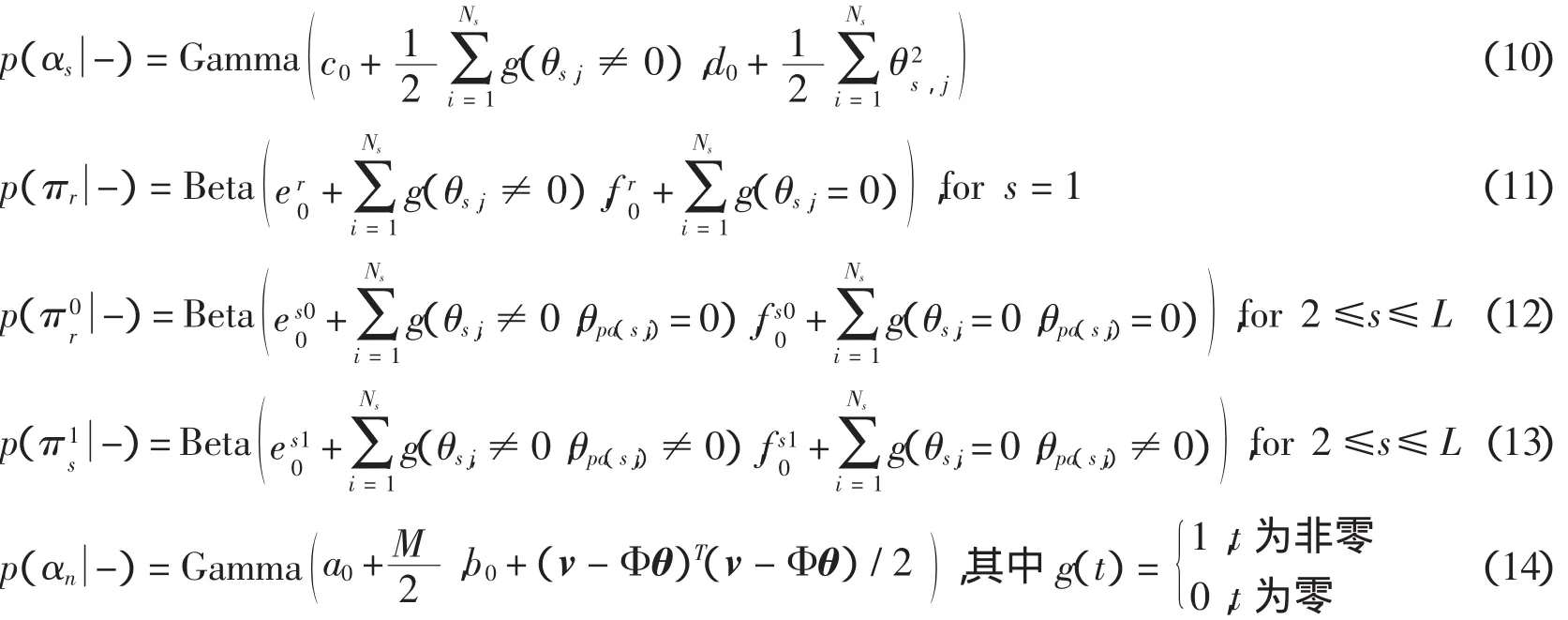
2.6 自适应背景建模
3 实验结果



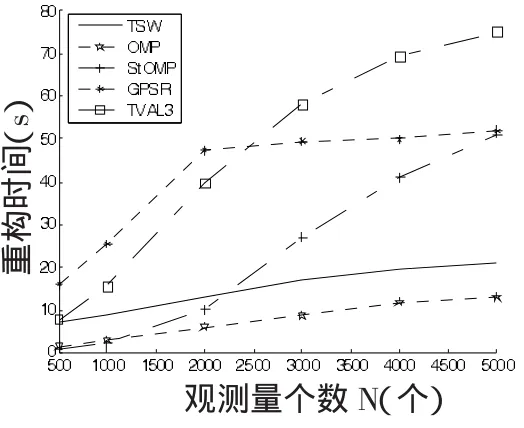
4 结束语
