PRM标量平流方案在GRAPES全球预报系统中的应用

苏勇 沈学顺 彭新东李兴良伍湘君张爽陈贤

1南京信息工程大学大气科学学院，南京210044

2中国气象科学研究院灾害天气国家重点实验室，北京100081

3中国气象局数值预报中心，北京100081

4广州空军气象中心，广州510071

1 引言

标量平流过程的数值模拟，一直是数值模式动力过程发展的重要内容。对于天气、气候模式来说，通常需要求解水汽等标量的平流输送方程。因为大气中水汽的分布具有梯度大、不连续、多相变等特点，这就给水汽平流过程的精确模拟带来一定的困难（苏勇和沈学顺，2009）。一个好的标量平流方案一般具备以下几个特点（Machenhauer et al.,2008）：（1）较高的计算精度；（2）严格的质量守恒；（3）正定，没有明显的数值振荡；（4）保持被平流物理量的形状；（5）保证计算的稳定性；（6）较高的计算效率。

随着大型计算机的飞速发展，数值模式的分辨率日益提高，这就给平流过程的计算精度提出了更高的要求。对于拉格朗日模式而言，一般情况下，如果直接采用高阶精度的插值方案进行水汽的平流计算，频散误差较大，强梯度区域的数值振荡明显，不能保证水汽场的空间分布特点和正定、守恒的性质（沈学顺等，2011）。

近年来，与计算流体力学相关的领域都对标量平流过程进行了深入的研究。早期的研究主要基于欧拉方法，如 TVD（total variation diminishing）（Thuburn, 1996）方案，基于通量修正思路的FCT（flux-corrected transport）（Book et al., 1975）方案，基于Godunov方法的MUSCL（Monotone Upstreamcentered Schemes for Conservation Laws）（Colella,1985）方案，以及基于分段抛物线函数的 PPM（Piecewise Parabolic Method）（Colella and Woodward,1984）方案等。其中MUSCL和PPM方案在天气模式的设计中得到了广泛的应用和发展。国内 Yu（1994）提出了一个两步保形方案（TSPAS，Twostep Shape Preserving Advection Scheme），有效地改进了暴雨中尺度模式中水汽的计算。

欧拉方法容易做到被平流标量的守恒性，但也有不易克服的缺点：（1）积分时间步长受到 CFL（Courant-Friedrichs-Lewy）条件的限制；（2）相邻网格点的插值过程会导致系统的非局地发展。

20世纪80年代以后，基于半拉格朗日方法设计的标量平流方案发展迅速，在天气模式中得到广泛应用（Robert et al., 1985；Ritchie et al., 1995）。与传统欧拉方案相比，半拉格朗日方案可取较大得时间步长，积分效率较高，计算精度相当，在处理不连续问题的时候没有显著的频散（Staniforth et al.,1991）。但半拉格朗日平流方案也普遍存在问题，上游点处物理量的内插造成总量不能严格守恒（陈嘉滨和季仲贞，2004），在标量场的强梯度、不连续区域计算精度不高等。

Williamson and Rasch（1989）首先提出半拉格朗日平流方案的保形问题。他们采用三次 Hermite插值或者有理函数插值，结合斜率的修正来确保单调性。Bermejo and Staniforth（1992）设计出一个混合算法使传统的半拉格朗日方法转化为准单调的半拉格朗日（QMSL）方法，如在平滑的区域采用三次样条插值或者三次拉格朗日插值，在不太平滑的区域采用一阶迎风格式，或者加大一阶迎风格式的权重。这种方法可以抑制强梯度和间断处的振动，同时在解足够光滑的区域保持了传统半拉格朗日方法的计算精度（沈学顺等，2011），但缺点明显：（1）在标量的强梯度、不连续区域，低阶插值不能保证计算精度；（2）传统的拉格朗日算法不能保证标量在全场的守恒性。

Xiao et al.（2002）和 Xiao and Peng（2004）从通量形式的平流方程出发，利用一个网格内的积分平均值和两边的边界值，设计出了PRM（Piecewise Rational Method）方案和 CSLR（Conservative SL with Rational function）方案，其中积分平均值通过通量来更新，边界值通过半拉格朗日点映射来更新。PRM方案是PPM方案的变形，用有理函数代替了PPM方案中的抛物线函数,利用有理函数的保凸性，避免了 PPM 中强制单调而采用的边界值调整。CSLR方案则是基于 CIP-CSL（Constrained Interpolation Profile-Conservative Semi-Lagrangian）（Tanaka et al., 2000; Xiao and Yabe, 2001）方法发展的一种使物理场精确守恒的半拉格朗日方法，它与 PRM 类似，但在边界值的计算上，它采用拟合出的曲线中上游点处的值来替换，而 PRM 则采用上游点处周围格点来插值。这两个方案无论在标量场的平滑处还是间断处，都可以做到正定保形，并保持较高的精度。虽然 CSLR的算法略简单于PRM，但CSLR中边界值是全局变量，在大规模并行计算中涉及相邻区域之间的数据交换，程序编制较复杂，通讯量较大。

中国气象局自主研发的新一代全球中期预报系统GRAPES_GFS（陈德辉和沈学顺，2006；庄世宇等，2005）采用半隐式半拉格朗日的动力框架，标量平流过程的计算采用QMSL方案。如前所述，该方案存在不光滑区域计算精度不高，不能严格守恒的问题。本研究将PRM标量平流方案引入GRAPES_GFS中，旨在改进模式对水汽平流和分布的模拟，提高降水的预报效果，提升模式的综合预报性能。

第二章简要介绍PRM标量平流方案、GRAPES_GFS中水汽方程以及对极区采用的技术处理；第三章通过一维、二维以及模式中的一系列理想试验对QMSL和PRM两种方案的性能进行对比；第四章通过GRAPES_GFS中的批量预报试验，检验采用PRM方案之后，对模式预报效果的改善；第五章给出本研究的结论。

2 方案简介

2.1 GRAPES_GFS中的水汽平流方程

GRAPES_GFS大气运动控制方程组（薛纪善和陈德辉，2008）中的水汽方程为

其中，q为水汽或其他水物质，S(q) 为水物质的源汇项，由物理过程部分计算。在不考虑源汇项的情况下，将方程（1）改写为通量形式：

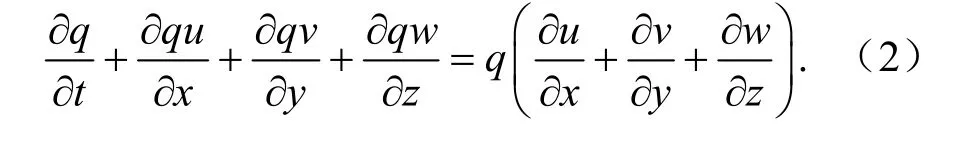
再将方程（2）推导到球面、地形追随坐标下，得到的水物质通量方程为

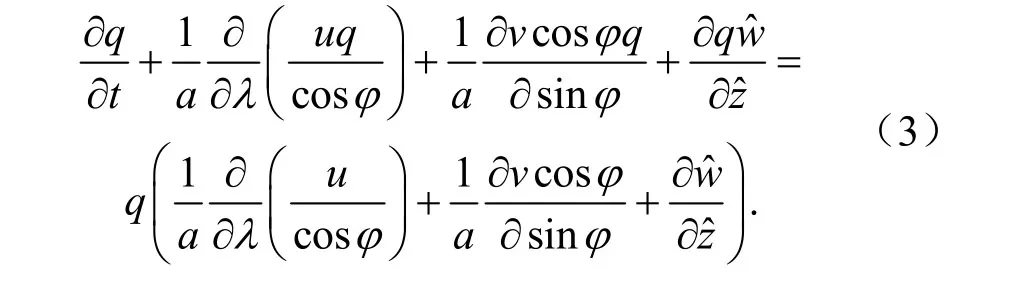
在上式中散度的推导过程中，暂未考虑地形坡度对散度的影响。u、v分别表示纬向、经向速度，表示地形高度追随坐标的高度，表示地形高度追随坐标下的垂直速度，λ和ϕ为经度和纬度，a为采用薄层近似之后的地球半径。

利用分维算法，将方程（3）改写到三个方向分别进行计算：

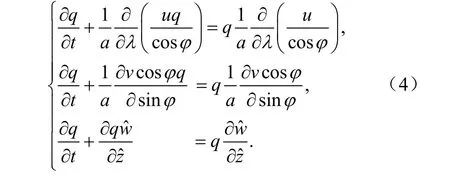
方程组（4）中三个方程的左边部分通过一维的平流方程分别计算，右边部分通过平流之后的散度修正过程计算。

分维算法易于实现，在多维平流及计算中得到广泛的应用，但是当流场中在x或y方向有辐合辐散的情况下，该算法会引入虚假的源汇。如果不对这种公式分解过程中产生的差异进行处理，那么模式在速度场散度较大的区域拟合出的水汽场和降水场是不合理的，会有明显的格点堆积问题，且易引发积分不稳定。Clappier（1998）提出了一种加入修正项的分维算法，在很大程度上缓解了这一问题。本研究采用的即为这种加入修正项的分维算法。

2.2 PRM标量平流方案（Xiao and Peng, 2004）

考虑通量形式的一维平流方程：

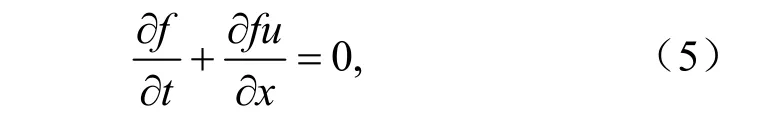
其中，f为被平流标量，t为时间，x为空间坐标，u为速度。将上式在控制单元格 [xi−1/2,xi+1/2]内积分，经过推导可以得到

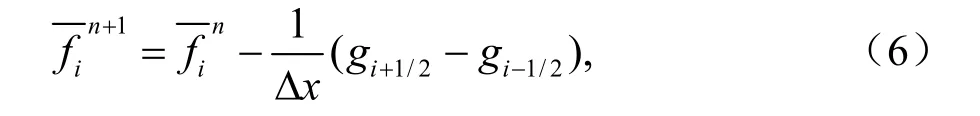
其中，n为积分时刻，Δx=xi+1/2−xi−1/2，gi±1/2分别代表第i单元格左右边界的通量。表示第i单元格的积分平均值，

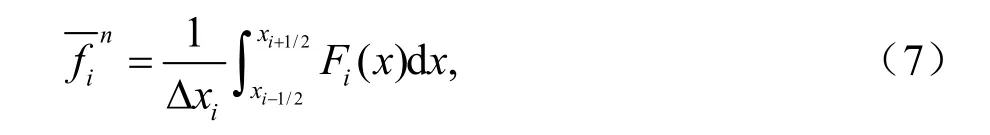
其中，Fi(x)表示第i单元格内所用算法拟合出的函数。PRM 算法采用如下的有理函数拟合计算区间内的标量分布形式：

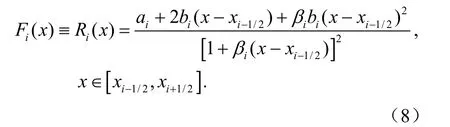
在积分平均值和单元界面值的限制条件下，

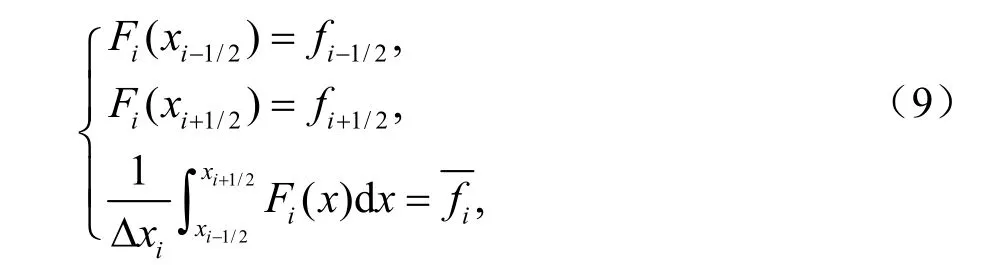
fi±1/2分别为第i单元格左、右边界的值。由（8）、（9）可以求得Ri(x)中参数的值：

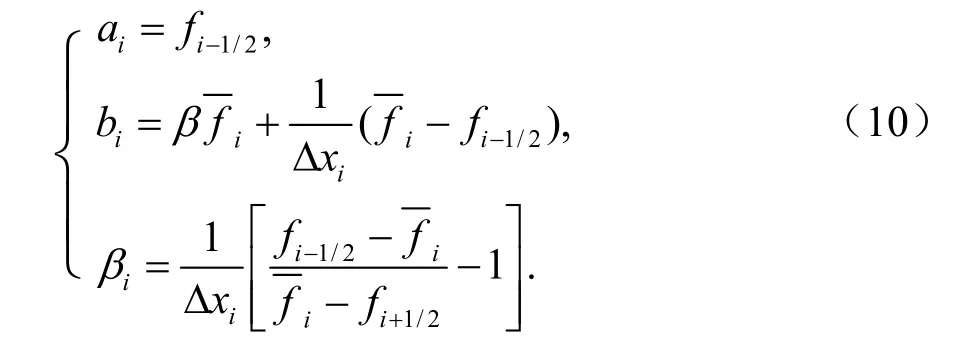
现在，只要再确定了边界值1/2if±，就可以确定函数()Fx。PRM 方案利用临近网格点的积分平均值插值得出边界值（Colella and Woodward，1984）。

这样，有理函数Ri(x)构造完成，就可由方程（6）、（7）来计算+1。方程（6）中边界通量g

i±1/2的表达式如下:

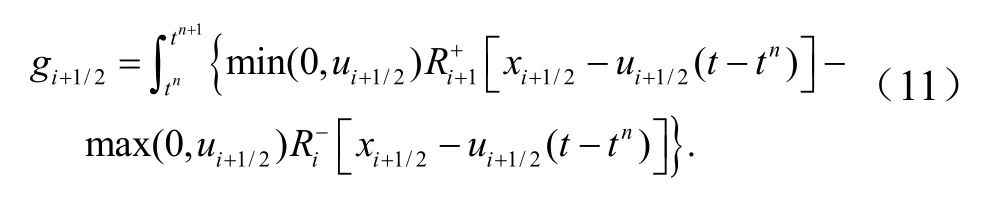
可以得到：

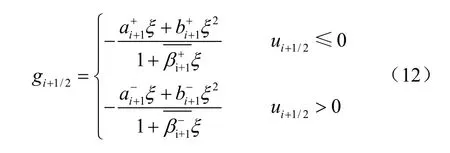
2.3 极地混合（Peng et al., 2005）

GRAPES_GFS采用球面经纬度格点坐标，变量在网格上的分布采用 Arakawa-C跳点方案，水物质放置在半点上，极点只放置经向风分量。在球面经纬度格点坐标中，纬向格距在极点附近变得非常小，如不采取特殊处理会导致积分不稳定。因为极点附近水物质含量一般不高，且极区附近四季都以绕极地的纬向风为主，经向风分量不大，所以极点附近水物质的分布和变化对高纬度地区影响不大。由此，引入极地混合技术，对极点附近小范围内的水物质进行混合。考虑到混合区域与未混合区域的过渡问题，本研究对传统的混合技术做了修正，采取了带过渡的极地混合。

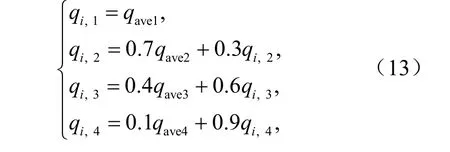
其中

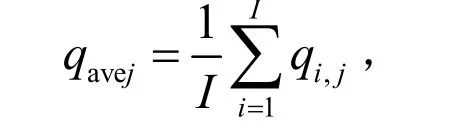
I为纬向格点总数，j=1，2，3，4分别对应从极点向赤道数的放置水物质的第1、2、3、4个纬圈，q为水物质的浓度在格点内的积分平均值，avejq为对应的第j个纬圈上q的平均值。

采用了考虑过渡的极区混合技术之后，PRM 平流方案在极区的适应能力明显增强，积分稳定性也得到了保证。但是当极区经向风较强时，极区的混合会带来一定的偏差，具体可以参考本文GRAPES_GFS中示踪标量穿越极地的理想试验。

3 理想试验

将 PRM标量平流方案加入 GRAPES_GFS之前，需要通过一系列的理想试验对其计算精度、频散性、耗散性等进行检验，同时与模式中现在采用的QMSL方案进行对比。该部分设计了4组理想试验：1D方波平流、2D圆锥平流、2D凹槽圆柱旋转和2D变形场试验。

为了定量检验数值试验的结果，定义误差如下：

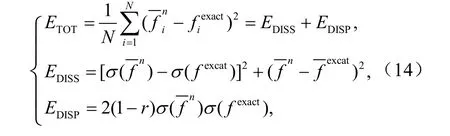
通过理想试验对PRM和QMSL平流方案的性能进行了检验和对比之后，将 PRM 方案加入GRAPES_GFS的动力框架中，进一步通过模式中球面上的理想试验，对该方案在模式中的合理性，以及在理想情况下的模拟效果进行检验和对比。

3.1 一维方波平流

一维的区域内有 100个格点，格距为1.0，水平均匀的速度场u=1.0，平流标量初始场分布如下：

在不同的时间步长，也就是不同的CFL数下模拟方波平流 50个格距后的分布形式。这里给出CFL数取0.5时的模拟结果。

表1 方波平流试验计算误差Table 1 Error of the square wave advection test

从图1和表1可以看出，QMSL和PRM方案都可以较好地保持方波的形状，没有相速度的误差，都可以完全抑制虚假的上冲和下冲。但相对来说，PRM比QMSL更接近真解，保形效果更好，总误差、耗散、频散误差都比较小。其他CFL条件下的模拟结果与此相类似。

3.2 凹槽圆柱旋转试验

二维均匀的区域在x、y方向都有100个格点，格距为 1.0，区域内为无辐合辐散、绕中心点顺时针匀速旋转的速度场，按下式给出：

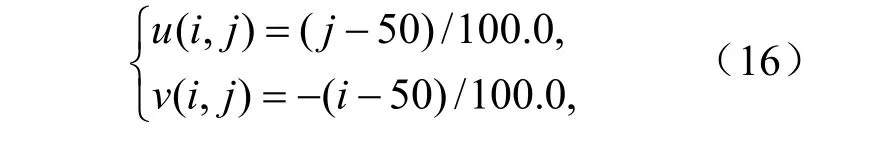
其中i、j为x、y方向格点数。初始场如图2所示，为中心在点（50，50），半径为25，高为1的带有凹槽的圆柱，凹槽的范围为4060,i≤≤2562j≤≤。时间步长取0.5，计算区域内CFL的最大值为0.25，积分12560步，即圆柱顺时针旋转10圈。图2和表2分别给出旋转2圈后和10圈后的结果以及计算偏差。

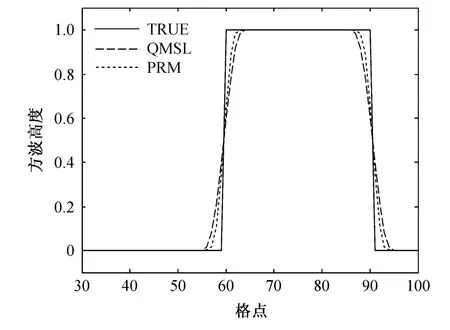
图1 方波平流试验模拟结果。纵坐标为方波高度; 实线为真解，长虚线为QMSL方案，短虚线为PRM方案Fig.1 The square wave advection test.The ordinate is the height of the square wave.The solid line is the true solution, long-dashed line for QMSL scheme and short-dashed line for PRM scheme

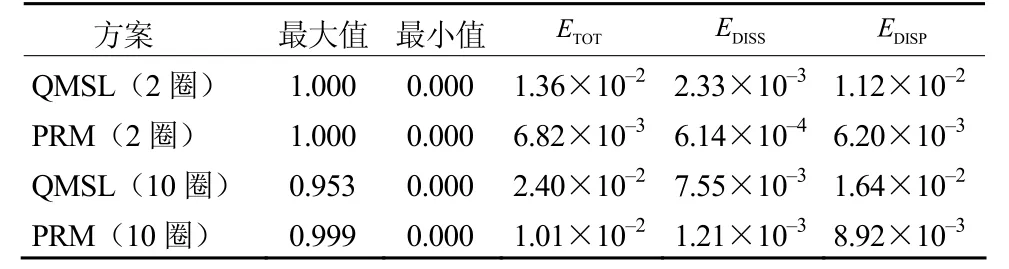
表2 凹槽圆柱旋转试验计算误差Table 2 Error of the cut-cylinder rotation test

该试验主要考察平流方案的保形能力，在没有辐合辐散的速度场中，初始场的分布形式不应该随着平流过程而发生变化。从图2中可以看到，在采用 QMSL方案旋转 2圈之后，已经不能够维持住凹槽圆柱的基本形状，旋转 10圈之后变形更加明显。相对来说在采用 PRM 方案的情况下，可以较好的保持初始场中凹槽圆柱的形状，变形较小。另外从表 2计算误差的对比中可以看到两个方案都没有虚假的下冲，QMSL方案在旋转 10圈之后，区域内的极值被削弱到0.953，而PRM方案还可以达到 0.999。频散、耗散误差的对比同样类似于前面两组理想试验，都是 PRM 方案的误差明显较小。

3.3 变形场试验

本节采用 QMSL和 PRM方案，重复了Smolarkiewicz（1982）和 Staniforth and Cote（1987）中的变形场试验。二维均匀的区域在x、y方向都有 100个格点，格距为 1.0。计算区域中采用带有很强辐合辐散的变形速度场，按照下式给出：

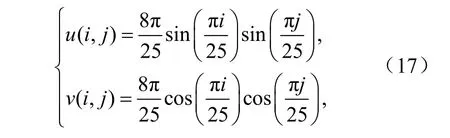
其中i、j为x、y方向格点数。初始场为中心在点（50，50），底面半径为15，高为3.87的圆锥。时间步长取0.7，计算区域内CFL的最大值为0.7。参考文献中给出的试验结果，这里也给出分别采用两种方案的情况下，积分19步、57步、3768步的试验结果，如图3中所示。

该试验主要考察平流方案在复杂变形速度场中的适应能力，经过长时间的积分，数值解应该对称地分布在中间两个涡旋的内部。这里给出的PRM方案模拟结果与Staniforth and Cote（1987）中的解析解相近，模拟结果中体现出了很好的对称性，但QMSL方案模拟结果的对称性稍差，与解析解偏差较大。对比两个方案的模拟结果，积分3768步之后，数值解中的最大值都要小于初始场中的最大值3.87，体现出计算方案的耗散性质，所以两个方案都具有较好的积分稳定性，相对来说QMSL方案耗散更大、更稳定。

3.4 GRAPES_GFS中的理想平流试验

在完成上面一系列理想试验之后，将PRM方案加入GRAPES_GFS的动力框架中，检验该方案在模式球面经纬度坐标中的模拟能力。

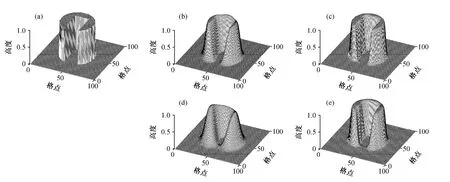
图2 凹槽圆柱旋转试验模拟结果。（a）为初始时刻的凹槽圆柱；（b）、（d）分别为QMSL方案旋转2圈和10圈后的结果；（c）、（e）分别为PRM方案旋转2圈和10圈后的结果。纵坐标为圆柱高度Fig.2 The cut-cylinder rotation test.(a) The initial moment of cut-cylinder; (b), (d) the results of QMSL scheme after 2 laps and 10 laps, respectively; (c),(e) same as (b), (d), but for PRM scheme.The ordinate is the height of the cylinder

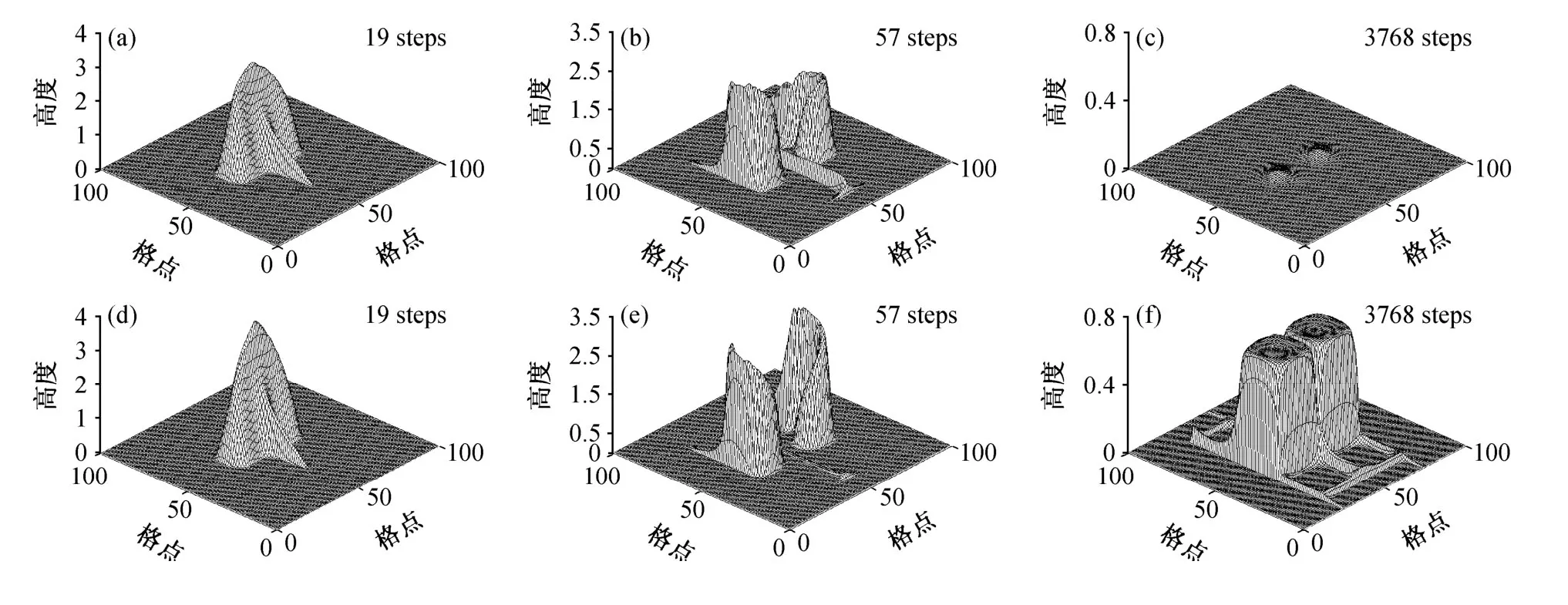
图3 变形场试验模拟结果。（a）、（b）、（c）依次为QMSL方案积分19、57、3768步后的模拟结果；（d）、（e）、（f）依次为PRM方案的对应结果。纵坐标为变形后圆锥的高度Fig.3 The deformational flow test.(a), (b), (c) The result of QMSL scheme after 19 steps, 57 steps, and 3768 steps, respectively; (d), (e), (f) same as (a), (b),(c), but for PRM scheme.The ordinate is the height of the cone after deformation

本试验中，等经纬度网格的格距 Δx=Δy= 0.5°,层顶高度ztop= 1.2 km，均匀分为60层。在球面上放置如下定义的示踪物初始场，如图4中所示。

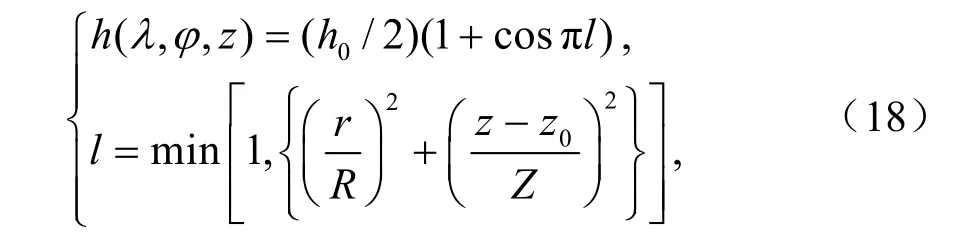
其中，λ和ϕ分别为经度和纬度，h0= 1.0g/kg，r是球面上距离圆心的大圆距离，水平半径R取1/3的地球半径，圆心的垂直高度取为4.5 km，垂直半径Z取1 km。

驱动示踪物进行平流的速度场如下设置：

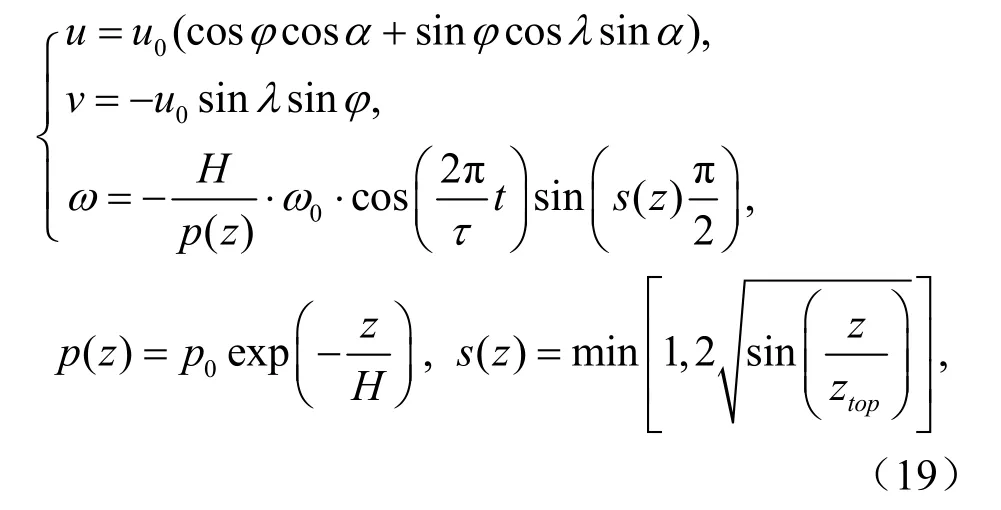
其中，u0= 38.61 m/s，α为平流方向与赤道的夹角，p0= 1000hPa，运动的尺度H≈ 8.78km。垂直运动的周期为4天，垂直速度的最大值约为4 m/s。初值以及试验条件的设置参考 Hundsdorfer and Spee（1995）、Li et al.（,2006）、Jablonowsik et al.（,2008）。

本部分进行三组试验，参考图4中平流方向的示意，分别对应（1）α=0°，示踪物向西，沿线路1绕地球一周回到初始位置；（2）α=45°，示踪物向东南，沿线路2绕地球一周回到初始位置；（3）α= 90°，示踪物向南，沿线路3绕地球两极一周回到初始位置。时间步长Δt=1200s，积分864步，12天之后示踪标量回到初始位置。

如图5中所示，在3组试验中，两个平流方案的模拟结果都较为合理，绕地球一周之后，示踪物的分布形式与初始场可以保持基本一致，没有位相偏差，中心的极值都有所削弱。但对比之后可以看出，QMSL方案耗散严重，中心极值由1.0耗散至0.6，PRM方案则可以使极值维持在0.8或者0.9；QMSL方案变形严重，x–z剖面的圆形已经明显扭曲，PRM 方案则可以很好地保持住初始场圆形的形状。

虽然 PRM 方案在前面的理想试验中表现较好，但是由于采用了极地混合的方案，当经向风分量为主的时候，也就是在90α=°的试验中，示踪物过极地时会有明显的相位以及量值的偏差，如图 6中水平剖面图所示。在实际预报的过程中，当过极地气流较强时，PRM方案也会带来类似的偏差，这点值得注意。

在没有源汇项的情况下，标量的平流过程应该保证区域内总质量的守恒。从图7的对比结果中可以看到，模式中原来采用的 QMSL方案并不能保证标量总质量的守恒，在α=0°的试验中，积分约12天，绕地球一周之后，总质量减少了约 1%；在α= 45°的试验中，总质量增加了约 3.5%；在α= 90°的试验中，两次穿越极地的过程中总质量都有明显的抖动，误差最大时可以达到0.5%。从图中的变化趋势可以预测，如果延长积分时间，在采用QMSL方案的情况下模式中标量的总质量还会持续的增大或减小。另一方面，采用欧拉通量形式处理标量平流过程的PRM方案则可以做到严格守恒，上面三组试验中标量在全球的总质量都不随积分发生变化。

通过上述一系列的理想试验，我们可以看出，PRM 标量平流方案相对于模式中原来使用的QMSL方案，精度更高，频散、耗散误差更小，正定、保形能力也更强，特别是处理标量场的不连续、强梯度区域优势明显；虽然在球面经纬度网格系统中需要采用额外的极地混合技术才能保证稳定积分，对过极地标量的模拟有一定的影响，但采用欧拉通量形式求解水汽方程的 PRM 方案可以保证积分过程中总质量的严格守恒，这一点对全球中期模式，特别是较长时间的积分来说非常重要。

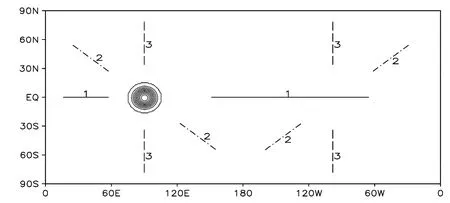
图4 球面理想试验初始场及平流方向示意图Fig.4 Schematic diagram of the initial field and the advection direction of the spherical ideal test

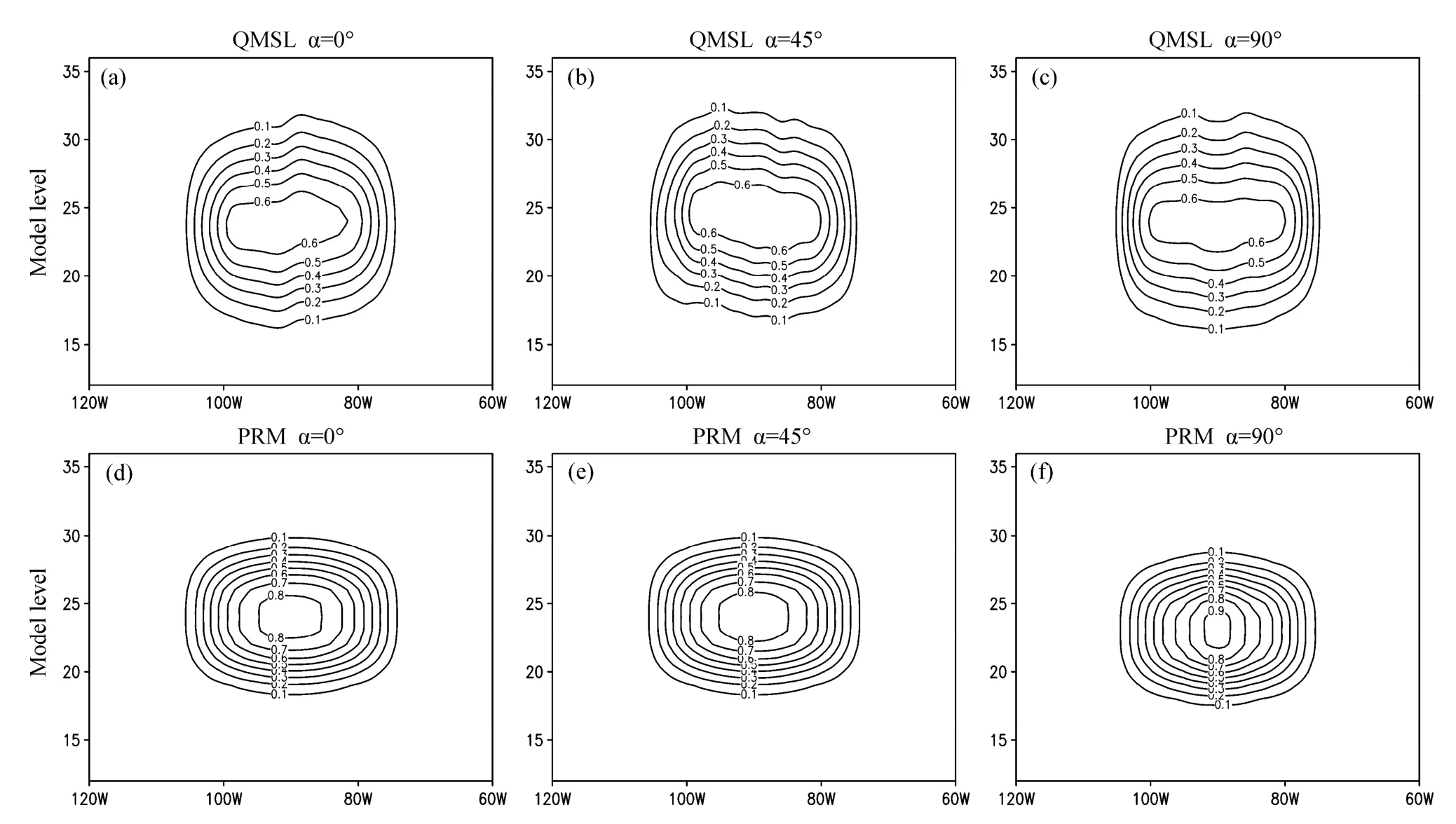
图5 球面理想试验，绕地球一周后示踪物浓度的模拟结果（x–z剖面，单位：g/kg）。（a）、（b）、（c）依次为QMSL方案在0α=°、45α=°和90α=°的模拟结果；（d）、（e）、（f）依次为PRM方案的对应结果。纵坐标为垂直方向模式层次Fig.5 The simulated concentration of the tracer after a turn around the earth in the spherical ideal test (x–z profile, units: g/kg).(a), (b), (c) The results of QMSL scheme for 0α=°, 45α=°, and 90α=°, respectively; (d), (e), (f) same as (a), (b), (c), but for PRM scheme.The ordinate is the vertical model levels

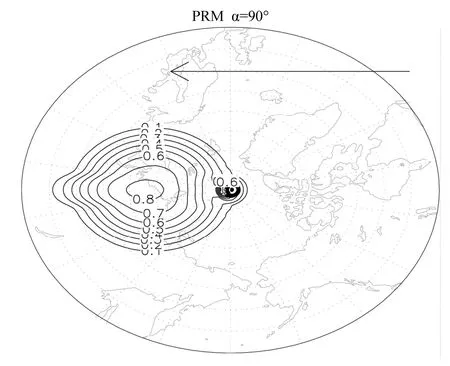
图6 PRM方案穿过极地时示踪物的示意图Fig.6 The schematic diagram while the tracer crosses the North Pole in PRM scheme

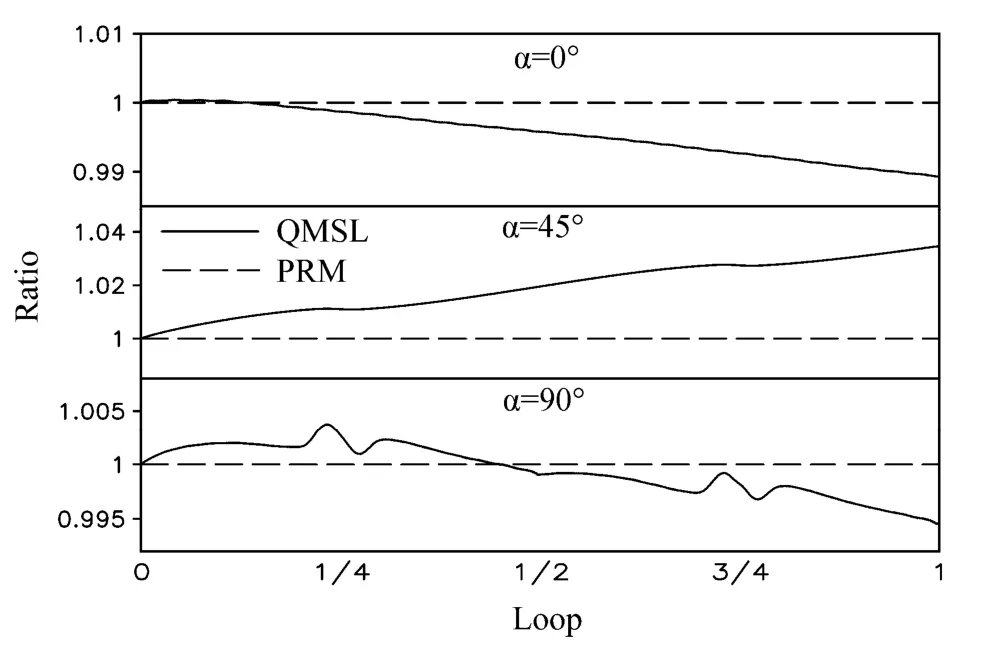
图7 球面理想试验中标量守恒性的对比。横坐标为绕地球的圈数，纵坐标为每步后全球总质量与初值的比例;实线为QMSL方案，虚线为PRM方案Fig.7 Conservation contrast of the spherical ideal test.The abscissa is the number of turns around the earth, the ordinate is the proportion of the global sum after each step to the initial value.Solid line: QMSL scheme;dashed line: PRM scheme

4 批量预报试验

上述理想试验确认了 PRM 方案在精度、守恒性及在保形方面的优势，本节将进一步通过在GRAPES_GFS中的实际预报试验，检验新方案对水物质平流、降水预报效果的改进，以及对模式综合预报性能的影响。

为此，共进行了连续一个月的8天预报试验，时间范围为2009年7月1日12时（协调世界时，下同）至7月31日12时。水平分辨率0.5°，垂直方向36层，时间步长600秒。积分初始场选择FNL再分析场，不做变分同化过程。试验所选取的物理过程参数化方案包括：WSM6微物理方案、RRTMG长短波辐射方案、CoLM（Common Land Model）陆面过程方案、MRF边界层参数化方案、SAS积云对流参数化方案。

下面通过对两种不同标量平流方案情况下湿度场、温度场、高度场、风场，以及水凝物和降水预报效果的对比，检验新标量平流方案对模式预报性能的改善。

从图8湿度场预报偏差的对比中可以看出，采用QMSL方案对水物质进行输送的时候，模式预报的中低层湿度场相对于FNL分析场明显偏湿，如图8a，72小时预报的850 hPa湿度场中，亚欧大陆、非洲大陆以及南、北美洲普遍偏湿1～3 g/kg，整个中国东部都是明显的偏湿区；在湿度场偏差的纬向平均剖面图（图8c）中，北半球低层平均湿度偏大6～8 g/kg，这种偏湿的趋势随着对流的运动可以延伸到500 hPa以上。当采用PRM方案之后，湿度场正偏差得到明显的缓解。从图8b中可以看到，整个亚欧大陆、非洲大陆以及南、北美洲的误差都得到明显的控制，图 8d中模式中层的湿度场正偏差也明显减小。但是在采用 PRM 方案之后，中低纬地区太平洋、大西洋以及印度洋上空湿度场的负偏差有所增大，模拟的大气明显偏干，具体原因还有待进一步的分析。

标量平流方案对模式的影响也不仅限于水物质分布和降水的模拟，通过相变加热、密度变化、各种不稳定机制等复杂的热力、动力过程，又影响着模式中温度场、高度场、风场等的预报。

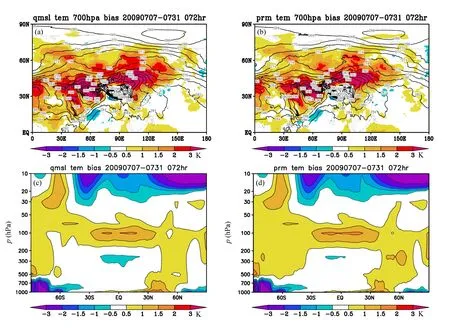
图9 批量试验72小时温度场预报平均偏差。单位：K。（a），（b）分别为QMSL方案和PRM方案700 hPa预报场与FNL的偏差，图中阴影为偏差，黑线为预报场；（c），（d）分别为QMSL方案和PRM方案预报场与FNL偏差的纬向平均垂直剖面Fig.9 Same as Fig.8, but for temperature forecast (units: K)

从图9a，b温度场72小时预报700 hPa偏差的对比中可以看出，采用QMSL方案的情况下，欧亚大陆上空有1～3 K左右的正偏差，采用PRM方案之后上述偏差得到明显的缓解。从图9c，d的垂直剖面图中也可以看到，采用新的PRM方案之后，模式中低层温度场的预报偏差有所减小，特别是在北半球中纬度地区效果明显。

预报场相对于分析场的距平相关系数（ACC）与均方根偏差（RMSE）可以很好地反映模式的预报能力，其中，ACC提高表示模式预报能力增强，RMSE减小表示模式预报偏差减小。从图10温度场北半球的ACC和RMSE可以看出：新的PRM方案对北半球温度场的预报有正贡献，模式的低层、中层、高层 ACC都有所提高；RMSE在中低层有所减小，高层基本保持不变。

进一步通过高度场的距平相关系数（ACC）与均方根偏差（RMSE）检验两种不同标量平流方案对高度场预报效果的影响。对比图11和图10可以看到，采用 PRM 方案之后，相对于给温度场带来的变化，对高度场的影响要更加明显：模式低层、中层、高层高度场距平相关系数都明显提高，均方根偏差都明显减小。

采用新的 PRM 标量平流方案之后，模式低层经向风场的预报偏差也有所减小，高原下游地区低层的南风正偏差有所缓解。图12a中，850 hPa高原东部南风明显偏强，相对于 FNL分析场风速偏大5 m/s左右，这种显著的偏差会对模式造成明显的影响，如降水带大范围北移等。采用 PRM 方案之后，如图12b所示，高原东部的南风偏差减小了约2 m/s，整个华北、东北地区的风场偏差也有所减小。

通过上面的几组对比可以看到，采用新的PRM标量平流方案之后，模式的综合预报能力明显提高，湿度场、温度场、高度场以及风场的预报偏差都有所减小，最后来检验水汽平流过程的改进对云的模拟，以及降水预报效果的影响。

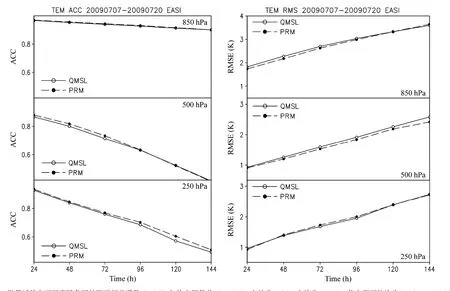
图10 批量试验东亚温度场各层的距平相关系数（ACC）与均方根偏差（RMSE）。左边为ACC，右边为RMSE。从上至下依次为850 hPa、500 hPa、250 hPa的结果；实线为QMSL方案；虚线为PRM方案Fig.10 The anomaly correlation coefficient (ACC) and root mean square error(RMSE) of temperature field in East Asia.Solid line with open circles: QMSL scheme; dotted line with solid circles: PRM scheme

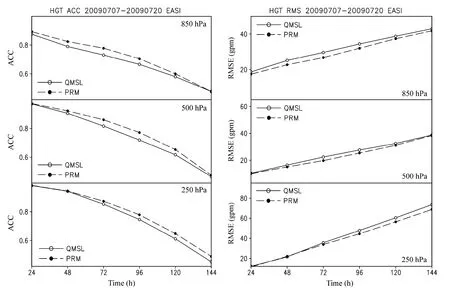
图11 批量试验东亚高度场各层的距平相关系数（ACC）与均方根偏差（RMSE）。左边为ACC，右边为RMSE。从上至下依次为850 hPa、500 hPa、250 hPa的结果；实线为QMSL方案；虚线为PRM方案Fig.11 Same as Fig.10, but for height field

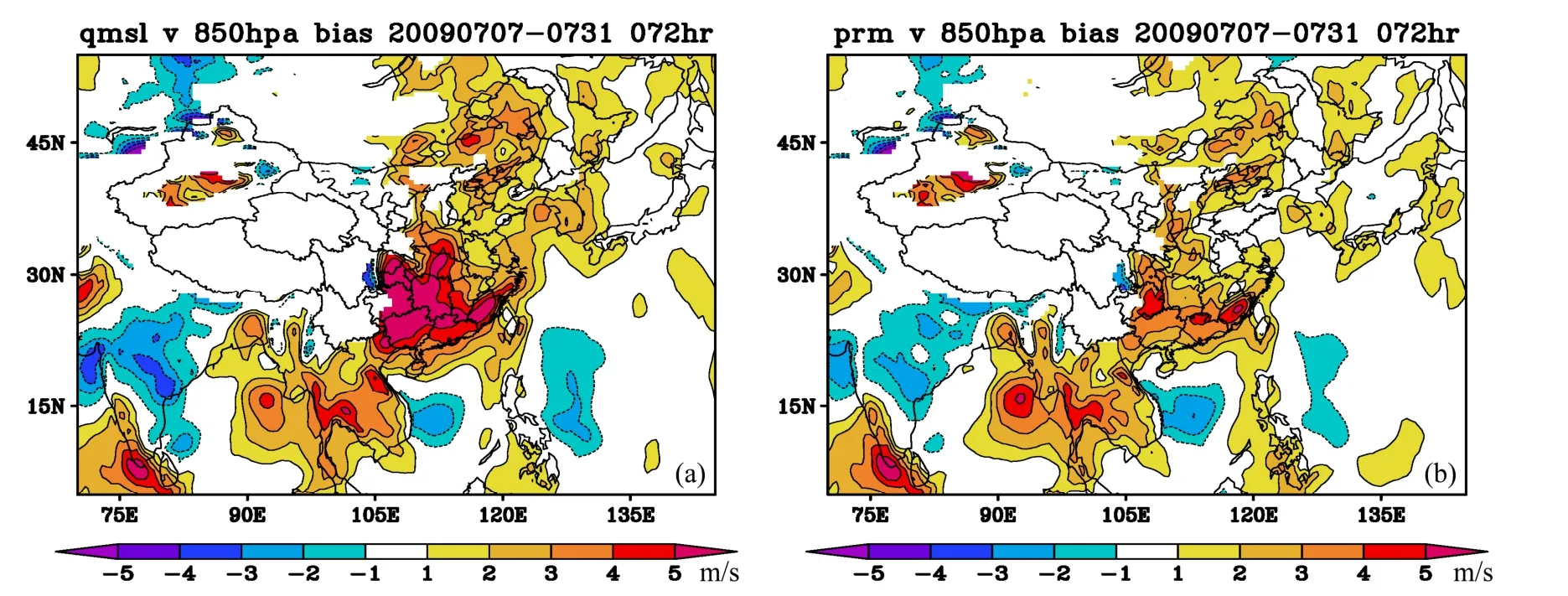
图12 批量试验72小时经向风场预报平均偏差（单位：m/s）。（a）为QMSL方案850 hPa预报场与FNL的偏差；（b）为PRM方案850 hPa预报场与FNL的偏差Fig.12 Average deviation of the 72-h meridional wind forecast at 850 hPa in the bulk test against FNL reanalysis data: (a) QMSL scheme; (b) PRM scheme

前面比较了模式预报的湿度场相对于 FNL分析场的偏差，但FNL分析场并不能真正的代表水凝物等的实况信息，相对来说，模拟的云带与卫星云图的对比、预报降水与实况降水的对比，更能体现出不同水物质平流方案在模式中的预报能力。下面通过对7月21～22日降水过程的个例分析，进一步的对比两种平流方案的预报性能。

为了与FY2C卫星云图做对比，将模拟的500 hPa以上总水凝物的浓度（云水、雨水、云冰、雪、霰）随高度进行积分（王明欢等，2011），得到模拟云带的分布，如图 13a，b所示。将两种方案模拟的云带与图 13c中 FY2C卫星云图对比可以看出，两种方案在大体上都可以把握住云带的位置、形状与量级，相对来说：（1）PRM方案预报的云带中心水凝物含量更高，更有利于对强降水过程的模拟；（2）QMSL方案没有模拟出河套、华北地区的云带，PRM方案的模拟结果与实况更为接近，但云带位置略有偏北。

另外，在24小时累积降水与实况的对比中可以看出，两种方案模拟的雨带在落区和走势上差别不大，在强度上略有差异，具体分析可以看到：（1）在强降水中心，PRM方案对降水量级的预报更加准确，如江淮流域、印度西北部、黑龙江地区等；（2）两种方案模拟的雨带落区差别不大，如都漏报了华北北部地区的降水，长江中下游地区的雨带位置都略有偏北等。

对全球中期预报系统来说，大范围、长时间系统的模拟能力非常重要。下面对亚洲区以及全球月平均的24小时累积降水进行对比，从图14中可以看出两种方案模拟的降水落区和走势上差别不大，在局部的强度上略有差异。对比中国区的月平均降水可以看出，相对于实况，QMSL方案在四川盆地、河套地区附近模拟出杂乱的大值中心；PRM方案模拟的雨带比较规则，与实况更加接近。从这点上可以看出，QMSL方案在地形复杂、水汽梯度大的区域模拟效果较差，PRM方案可以更好的处理这一类准不连续、大梯度问题。

7月份，赤道辐合带（ITCZ, intertropical convergence zone）偏向北半球,从西太平洋暖池向东南伸展的南太平洋辐合带（SPCZ, southern Pacific convergence zone）也比较明显。从图14e，f全球的月平均降水中可以看出，两种方案模拟的降水差异不大，都与实况较为接近；两种方案都可以把握住ITCZ和SPCZ区域降水的位置与走势，只是在局部强度上略有差异。

通过全球 24小时累积降水月平均的纬向平均也可以较为直观的对比两种标量平流方案下，GRAPES_GFS对各纬度地区平均降水量的预报能力。从图15中可以看出：（1）整体来说，两种方案模拟的降水没有大的差异；（2）ITCZ区域，PRM方案模拟的降水偏强，QMSL方案与实况更为接近；（3）60°S附近和40°N附近，两种方案模式的降水都较实况偏弱。

下面通过 Threat Score（TS）和 BIAS score（BAIS）评分检验，对批量预报试验期间各降水量级的降水量以及落区偏差进行定量地检验。评分的区域为东亚区域（15°～65°N，70°～145°E）。简要介绍这两种评分方法（王明欢等，2011）：TS评分主要用来对降水的量级进行定量检验；bias评分又称为偏差评分，主要是对降水落区的偏差进行定量检验。这两种评分都是基于累加量级的方法，即分别对大于某一阈值的预报情况进行检验，若预报和实况均为大于此量级的降水即为预报正确。这两种评分都是数值越接近1.0，代表预报效果越好。

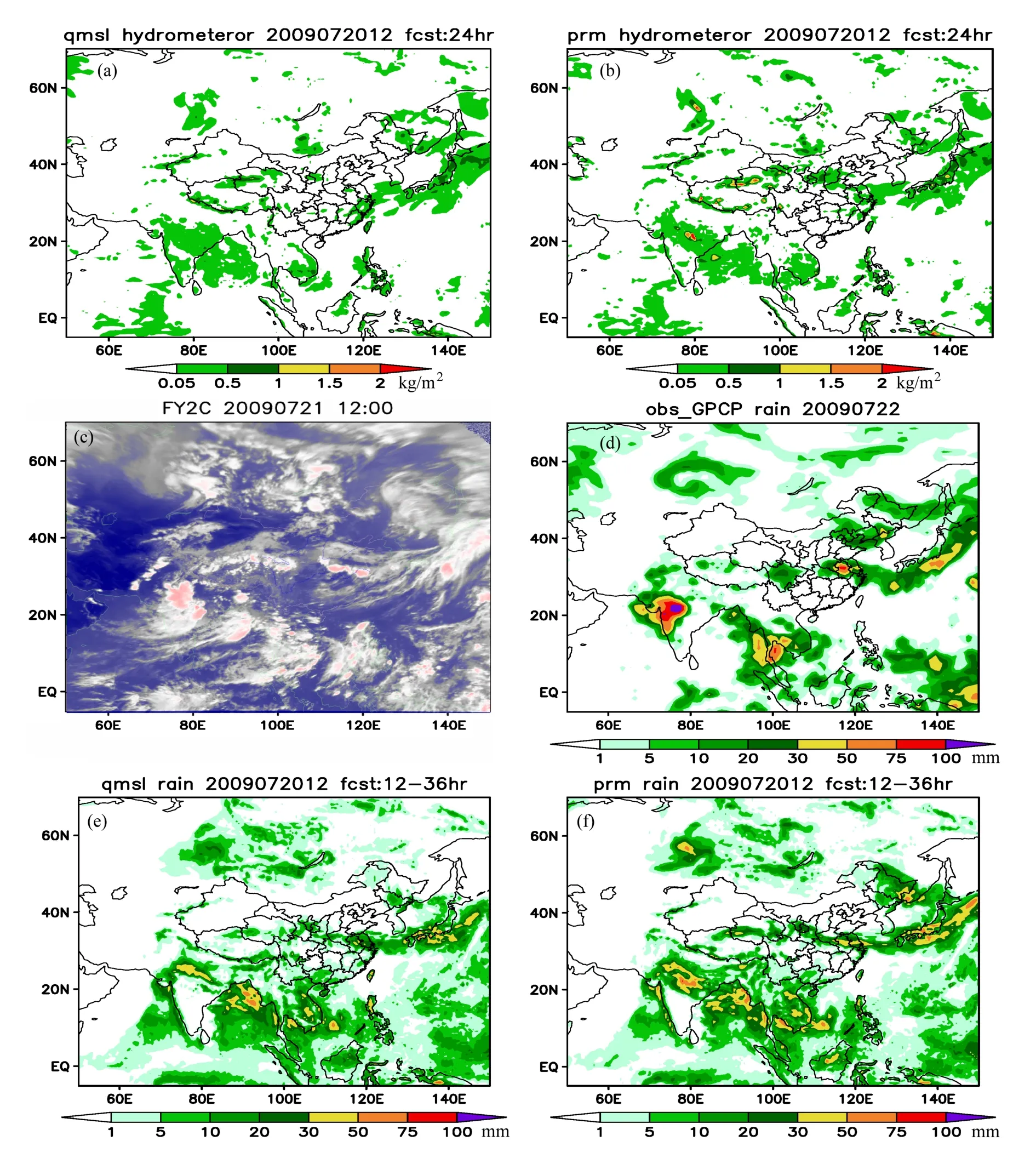
图13 （a），（b）分别为QMSL和PRM方案2009年7月20日12时24 h预报的云带分布（单位：kg/m2）；（c）风云2C卫星2009年7月21日12时的卫星云图；（d）GPCP资料2009年7月22日00时的24 h累积降水量（单位：mm）；（e），（f）分别为QMSL和PRM方案2009年7月20日12时预报的12～36 h时段内24 h累积降水量（单位：mm）Fig.13 (a), (b) 24-h cloud band forecast at 1200 UTC 20 July 2009 for QMSL and PRM schemes; (c) nephogram of the FY-2C satellite at 1200 UTC 21 July 2009; (d) 24-h accumulated precipitation from GPCP data at 0000 UTC 22 July 2009; (e), (f) the 12–36-h accumulated precipitation at 1200 UTC 20 July 2009 for QMSL and PRM schemes

从图16东亚区域降水的检验结果来看，对降水量级的TS检验中，对于24 h累积大于10 mm的降水，PRM方案模拟的降水量级更加准确，但对于降水量在100 mm以上的大暴雨、特大暴雨，模式的预报能力较差；对落区偏差的BAIS评分中可以看到，对于各个量级的检验，PRM方案的BAIS值都更加接近1.0，模拟的降水落区都与实况更加接近。

虽然水物质平流的模拟对降水非常重要，但它不是决定降水的唯一因素，比如水物质之间的相变过程、积云对流、辐射的加热作用等都在降水的产生过程中发挥关键的作用。想要更好的模拟降水过程，不仅需要更好的标量平流方案，还需要更合理的物理过程参数化方案。

在这一部分中通过批量实际预报对 PRM 标量平流方案在 GRAPES_GFS中的预报效果进行了检验，对比QMSL方案的模拟效果可以看到：（1）PRM方案明显地减小了中低层湿度场的正偏差；（2）采用 PRM 方案之后，对温度场、高度场、风场的模拟都有正的贡献；（3）两种方案模拟的云带、降水带没有大的差异，相对而言，PRM方案对中雨及以上量级的降水模拟的更加准确，东亚区的 TS和BAIS评分都更优，特别是在地形复杂、水汽梯度大的区域模拟的降水带更加合理。

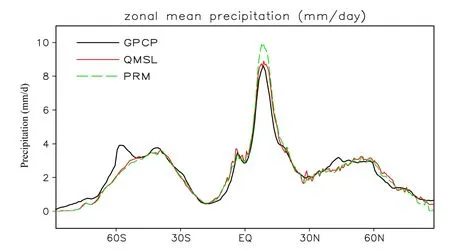
图15 批量试验36～60 h预报时段内24 h累积降水量平均值的纬向平均。黑色实线为GPCP资料；红色实线为QMSL方案；绿色虚线为PRM方案Fig.15 The zonal average of the averaged 24-h accumulated precipitation in the 36–60-h period in the bulk test.Solid black line: GPCP data; solid red line:QMSL scheme; dashed green line: PRM scheme

图16 批量试验东亚区域降水的TS和BAIS评分。左边为TS评分，右边为BAIS评分。从上至下依次为12～36 h、36～60 h和60～84 h的评分结果。实线为QMSL方案；虚线为PRM方案Fig.16 The Threat Score (TS) and BIAS score (BAIS) of the precipitation in East Asia in the time periods of 12–36 h, 36–60 h, and 60–84 h in the bulk test

5 结论

PRM方案是Xiao and Peng（2004）利用单元格内的积分平均值和两个边界值构造的基于分段连续有理函数的半拉格朗日标量平流方案，本研究将其引入GRAPES_GFS，把模式中水汽方程改写为通量形式后利用其求解，在得到高精度、正定保形数值解的同时，可以保证积分过程的严格质量守恒。在经过一系列单机上的理想试验、模式动力框架中的理想试验、批量的实际预报试验之后，得到以下几点主要结论：

（1）PRM方案相对于QMSL方案，精度更高，频散、耗散误差更小，正定、保形能力也更强，特别是处理标量场的不连续、强梯度区域优势明显。

（2）GRAPES_GFS中，PRM方案在欧拉格点上求解通量形式的水汽方程，可以保证水物质在积分过程中的严格守恒，这一点对全球中期模式，特别是积分时间较长的情况来说非常重要；原来的准单调半拉格朗日（QMSL）方案不能保证标量的守恒性。

（3）在实际预报中，相对于QMSL方案，PRM方案明显地减小了中低层湿度场的正偏差；两种方案模拟的云带、降水带差异不大，相对而言，PRM方案对中雨及以上量级的降水模拟的更加准确，东亚区的TS和BAIS评分都更优，特别是在地形复杂、水汽梯度大的区域模拟的降水带更加合理。

（4）标量平流方案对模式的作用不仅局限于水物质和降水的模拟，通过模式中的热力、动力过程又影响着温度场、高度场、风场等。GRAPES_GFS中采用PRM方案之后，对模式温度场、高度场、风场的模拟都有显著的正贡献。

本论文的研究工作取得了一些有意义的结果，但数值模式需要靠有限的方程组去求解大气中复杂的动力、热力过程，一个算法在模式中的应用也远比做理想试验要复杂。本研究将 PRM 方案引入GRAPES_GFS之后，也还有一些需要进一步解释和解决的问题：

（1）当采用 PRM 方案之后，亚欧大陆、非洲大陆以及南、北美洲地区低层湿度场正偏差都得到明显的控制，但中低纬地区太平洋、大西洋以及印度洋上空湿度场的负偏差有所增大（图7b，d），模拟的大气明显偏干，具体原因还有待进一步的分析。

（2）将PRM方案引入GRAPES_GFS之后，由于经纬度网格在极区的格点辐合问题，需要采用极地混合技术来保证积分的稳定性，这对极地地区的精确模拟有一定的影响。

（References）

Bermejo R, Staniforth A.1992.The conversion of the semi-Lagrangian advection schemes to quasi-monotone schemes [J].Mon.Wea.Rev., 120:2622–2632.

Book D L, Boris J P, Hain K.1975.Flux-corrected transport II:Generalizations of the method [J].J.Comput.Phys., 18: 248–283.

陈德辉, 沈学顺.2006.新一代数值预报系统GRAPES研究进展 [J].应用气象学报, 17: 773–777.Chen D H, Shen X S.2006.Recent progress on GRAPES research and application [J].Journal of Applied Meteorological Science (in Chinese), 17: 773–777.

陈嘉滨, 季仲贞.2004.半隐式半拉格朗日平方守恒格式的构造 [J].大气科学, 28: 527–535.Chen J B, Ji Z Z.2004.A study of complete square-conserving semi-implicit semi-Lagrangian scheme [J].Chinese Journal of Atmospheric Sciences (in Chinese), 28: 527–535.

Clappier A.1998.A correction method for use in multidimensional time-splitting advection algorithms: Application to two- and threedimensional transport [J].Mon.Wea.Rev., 126: 232–242.

Colella P.1985.A direct Eulerian MUSCL scheme for gas dynamics [J].Sci.Stat.Comput., 6: 104–117.

Colella P, Woodward P R.1984.The piecewise parabolic method (PPM) for gas-dynamical simulations [J].J.Comput.Phys., 54: 174–201.

Hundsdorfer W, Spee E J.1995.An efficient horizontal advection scheme for the modeling of global transport of constituents [J].Mon.Wea.Rev.,123: 3554–3564.

Jablonowsik C, Lauritzen P, Nair R, et al.2008.Idealized test cases for the dynamical cores of atmospheric general circulation models: A proposal for the NCAR ASP 2008 summer colloquium.June, 2008, Boulder,Colorado, U.S.A., NCAR.

Li X L, Chen D H, Peng X D, et al.2006.Implementation of the semi-Lagrangian advection scheme on a quasi-uniform overset grid on a sphere [J].Adv.Atmos.Sci., 23: 792–801.

Machenhauer B, Kass E, Lauritzen P H.2008.Finite-Volume Methods in Meteorology [C] // Teman R, Tribbia J, Ciarlet P.Computational Methods for the Atmosphere and the Oceans.New York: Elsevier, 1–120.

Peng X D, Xiao F, Wataru O, et al.2005.Conservative semi-Lagrangian transport on a sphere and the impact on vapor advection in an atmospheric general circulation model [J].Mon.Wea.Rev., 133: 504– 520.

Ritchie H.1995.Implementation of the semi-Lagrangian method in a high resolution version of the ECMWF forecast model [J].Mon.Wea.Rev.,123: 489–514.

Robert A, Yee T L, Ritchie H.1985.A semi-Lagrangian and semi-implicit numerical integration scheme for multilevel atmospheric models [J].Mon.Wea.Rev., 113: 388–394.

沈学顺, 王明欢, 肖峰.2011.GRAPES模式中高精度正定保形物质平流方案的研究 I: 理论方案设计与理想试验 [J].气象学报, 69: 1–15.Shen X S, Wang M H, Xiao F.2011.A study of the high-order accuracy and positive-definite conformal advection scheme in the GRAPES model.Ⅰ: Scientific design and idealized tests [J].Acta Meteorologica Sinica(in Chinese), 69: 1–15.

苏勇, 沈学顺.2009.相变修正方案在GRAPES模式标量平流中的应用[J].气象学报, 67: 1089–1100.Su Y, Shen X S.2009.Application of amendment to phase-change scheme in scalar advection of GRAPES model [J].Acta Meteorologica Sinica (in Chinese), 67: 1089–1100.

Smolarkiewicz P K.1982.The multi-dimensional Crowley advection scheme [J].Mon.Wea.Rev., 110: 1968–1983.

Staniforth A, Côté J.1991.Semi-Lagrangian integration schemes for atmospheric models—A review [J].Mon.Wea.Rev., 119: 2206–2223.

Staniforth A, Cote J, Pudykiewicz J.1987.Comments on “Smolarkiewicz_s deformational flow” [J].Mon.Wea.Rev., 115: 894–900.

Tanaka R, Nakamura T, Yabe T.2000.Constructing exactly conservative scheme in a non-conservative form [J].Comput.Phys.Commun., 126:232–243.

Thuburn J.1996.TVD schemes, positive schemes, and the universal limiter[J].Mon.Wea.Rev., 125: 1990–1997.

王明欢, 沈学顺, 肖峰.2011.GRAPES模式中高精度正定保形物质平流方案的研究II: 连续实际预报试验 [J].气象学报, 69: 16–25.Wang M H, Shen X S, Xiao F.2011.A study of the high-order accuracy and positive-definite conformal advection scheme in the GRAPES model.Ⅱ:Continuous actual rainfall prediction experiments [J].Acta Meteorologica Sinica (in Chinese), 69: 16–25.

Williamson D L, Rasch P.1989.Two-dimensional semi-Lagrangian transport with shape preserving interpolation [J].Mon.Wea.Rev., 117:102–129.

Xiao F, Peng X D.2004.A convexity preserving scheme for conservative advection transport [J].J.Comput.Phys., 198: 389–402.

Xiao F, Yabe T.2001.Completely conservative and oscillation-less semi-Lagrangian schemes for advection transportation [J].J.Comput.Phys., 170: 498–522.

Xiao F, Yabe T, Peng X D, et al.2002.Conservative and oscillation-less atmospheric transport schemes based on rational functions [J].J.Geophys.Res., 107: 1–11.

薛纪善, 陈德辉.2008.数值预报系统GRAPES的科学设计与应用 [M].北京: 科学出版社, 67–70.Xue J S, Chen D H.2008.Scientific Design and Application on Numerical Prediction System GRAPES (in Chinese)[M].Beijing: Science Press, 67–70.

Yu R C.1994.A two-step shape-preserving advection scheme [J].Adv.Atmos.Sci., 11: 479–490.

庄世宇, 薛纪善, 朱国富, 等.2005.GRAPES全球三维变分同化系统——基本设计方案与理想试验 [J].大气科学, 29: 872–884.Zhuang S Y, Xue J S, Zhu G F, et al.2005.GRAPES global 3D-Var system—Basic scheme design and single observation test [J].Chinese Journal of Atmospheric Sciences (in Chinese), 29: 872–884.