TI介质局部角度域射线追踪与叠前深度偏移成像

段鹏飞，程玖兵＊，陈三平，何光明

1 同济大学海洋与地球科学学院，上海 200092

2 中国石油川庆钻探工程有限公司地球物理勘探公司，成都 610213

1 引 言

为了改善地震波照明与成像、噪声压制以及油气储层的预测和描述，长偏移距、宽方位的地震数据采集越来越多，以往针对有限偏移距、窄方位地震数据的各向同性介质假设与在此基础上的地震成像方法明显受到了挑战.忽略各向异性带来的误差会引起反射波归位不准，绕射波收敛不彻底，能量不聚焦，对长偏移距、宽方位数据尤为突出.这就要求地震偏移成像与速度模型建立方法考虑速度各向异性，否则花费巨大代价观测到的地震资料得不到合理的利用.大量的观测与研究发现，许多页岩与薄互层沉积地层等在地震波长尺度下均可等效成TI介质.而这些地层在全球范围内分布非常广泛.因此，在考虑各向异性地震波成像问题时，VTI介质和TTI介质是最常用的等效模型.

叠前深度偏移是强横向非均匀介质复杂构造成像与速度模型建立依赖的关键技术.其算法实现要么基于射线理论，如Kirchhoff偏移和高斯束偏移，要么基于波动理论，如单程波方程深度延拓偏移和双程波方程逆时延拓偏移.近10多年来，各向异性介质深度偏移方法也得到了极大的发展，先后出现了 TI介质 Kirchhoff偏移[1］、高斯束偏移[2］、单程波方程偏移[3］与逆时偏移[4］等深度域成像方法.尽管波动方程偏移存在精度上的优势，射线理论基础上的偏移方法因其在灵活性、面向局部目标的成像能力以及计算成本等优势，在复杂构造成像尤其是速度模型建立过程中得到广泛应用.目前主要地震数据处理软件中的深度域偏移速度模型构建都仍以Kirchhoff偏移作为引擎.

在复杂介质条件下，即使偏移速度是合理的，传统的偏移距域和炮域共成像点道集都可能存在假象干扰.为此，近十几年来人们一直在致力于研究射线理论或波动理论基础上的角度域成像方法.基于射线理论和广义拉冬变换（GRT），de Hoop[5］提出了共散射角偏移／反演理论.随后Xu等[6］和Brandsberg-Dahl等[7］提出了Kirchhoff叠前深度偏移共散射角成像方法，并用于地震成像和速度模型建立过程中.Bleistein[8］也系统地阐述了共散射角成像／反演理论.最近，Koren等[9］在局部角度域成像理论框架下提出了方向型和反射型共成像点道集的产生方法及其用途.Cheng等[10］提出了适应TI与方位各向异性介质的方位保真局部角度域叠前时间偏移成像方法并展示了在储层成像与描述中的初步应用.

局部角度域Kirchhoff叠前深度偏移算法的核心在于稳健、快速地计算地震射线的走时与方向信息.在传统Kirchhoff叠前深度偏移过程中，程函方程有限差分解法[11］与波前重建算法[12］被广泛用于走时表的计算[1，13］.然而，对局部角度域成像与反射走时层析基础上的偏移速度分析而言，射线追踪算法显得更有吸引力，因为它除了计算走时，还可以显式地得到射线路径及其方向信息.不过，传统的各向异性介质射线追踪方程是以刚度系数而不是Thomsen参数表示的[14］，不方便数值计算，效率也较低[14-16］.为此，一些学者重新推导了Thomsen参数表征的射线方程.例如，Alkhalifah[17］基于声学近似推导出了VTI介质的射线方程.Zhu[15-16］等推导了一种基于相速度、适用于一般各向异性介质的射线方程.

本文根据强横向非均匀各向异性介质地震波成像与偏移速度模型建立的需要，研究基于射线理论的TI介质局部角度域叠前深度偏移成像方法.首先讨论与对比两种各向异性射线追踪算法，然后论述局部角度域叠前深度偏移成像原理及其算法实现，最后借助国际上通用的理论模型检验算法的可靠性.

2 各向异性介质射线追踪方法

各向异性介质中的运动学射线方程最早由Cerveny[14］给出.下文简单回顾其推导过程.一般各向异性介质无源的弹性波动方程可以表示为

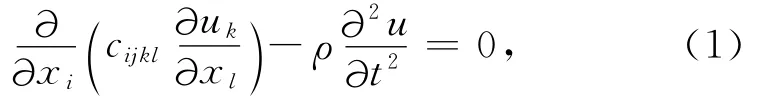
其中，ui为位移，cijkl为介质的刚度系数，i，j，k，l=1，2，3，ρ为密度，t为走时.其频率域表达式为

其中，ω为圆频率.在零阶射线理论中，（2）式的近似解可写成uk（xi，ω）=Uk（xi）eiωτ（xi），其中Uk（xi）和τ（xi）分别是射线上的振幅和走时.把这个解带入（2）式，当ω→ ∞ 时，可得到Christoffel方程：

其中，Γjk=aijklpipl为Christoffel矩阵，aijkl=cijkl／ρ为密度归一化刚度系数，pi=∂τ／∂xi为慢度矢量的各个分量.方程（3）对应一个标准的特征值问题，且特征值满足G（pi，xi）=1.（3）式可改写为

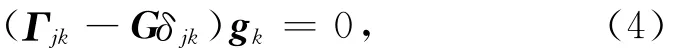
其中，gk是单位特征向量（即极化矢量）.（4）式两边同乘以gj，结合gkgk=1，可得到

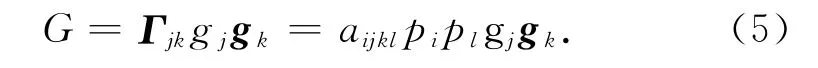
对于程函τ（xi），方程（4）是一个非线性一阶偏微分方程.这个程函方程可通过汉密尔顿方程求解，进而表示成一般各向异性介质的运动学射线追踪方程组[14］：

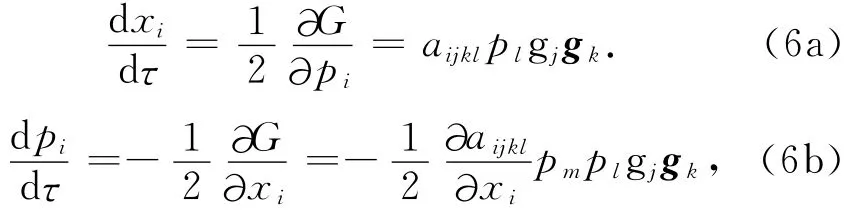
方程组等式最右侧的函数非常复杂，计算不但费时，且需要在射线追踪的每一步求解特征值问题.此外，方程组（6a）与（6b）用刚度系数来描述介质的弹性性质，这与实际地震资料处理中通常用Thomsen参数的情况不一致.为此，文中将讨论两种不需用刚度系数表征的各向异性射线方程.

2.1 相速度表示的各向异性介质射线方程

为了克服刚度系数表示的射线方程的复杂性及其计算上的麻烦，Zhu[15-16］等重新推导了各向异性介质中的运动学射线追踪方程.根据文献[14］，沿xi方向的群速度可表示为Vi=aijklplgjgk.于是，方程（6a）改写为

其中，VGi为群速度对空间坐标xi的导数.考虑到（4）式中特征值G及其偏导数∂G／∂xi都是pi的齐次方程，容易得到v2=G（xi，ni），故而有：

与各向同性介质程函方程推导思路一样，将平面波解带入方程（10）可推导出VTI介质的程函方程：

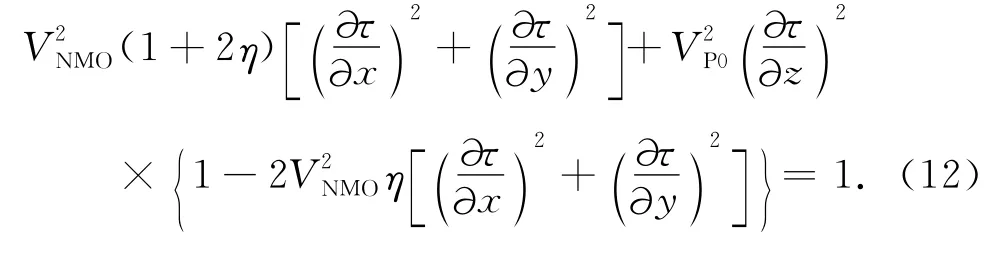
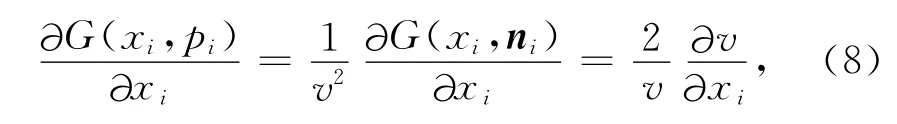
其中，ni为单位慢度矢量，v=v（xi，ni）为相速度.将（8）式带入方程（6b）并联立（7）式得到：

由于群速度可通过相速度计算得出，因此（9a）与（9b）式就组成了相速度表示、适应一般各向异性介质的射线方程组.这样就回避了传统各向异性射线追踪过程中每一步都要计算的特征值问题.注意，由于空间矢量x与单位慢度矢量n都是相速度方程v=v（xi，ni）的独立变量，因此（9b）式右边对相速度求偏导数时，其隐函数的链式求导中不依赖ni，只需对相速度表达式中出现的与空间坐标xi有关的参数对xi求导即可.

在许多地质条件下，受构造运动或其它因素影响，一些横向各向同性地层大多数情况下都非水平层状，其对称轴通常与垂向存在一定的夹角.这时，采用TTI模型来描述速度各向异性就更合理.附录A给出了VTI与TTI介质中相速度表示的射线追踪方程的具体形式.

2.2 TI介质声学近似意义下的射线方程

声学近似就是假设沿对称轴方向qSV波的传播速度为0，即VS0=0，这样就可将原始的VTI介质弹性波动方程及其频散关系简化.假设地下介质为声学介质，由VTI介质弹性波动方程及其频散关系可推导出近似的qP波标量波动方程，进而得到相应的程函方程和射线方程[17］.研究表明，声学近似对qP波运动学特征的负面影响基本可以忽略[17］.

根据VTI介质qP波的频散关系，声学近似qP波波动方程满足[17］：

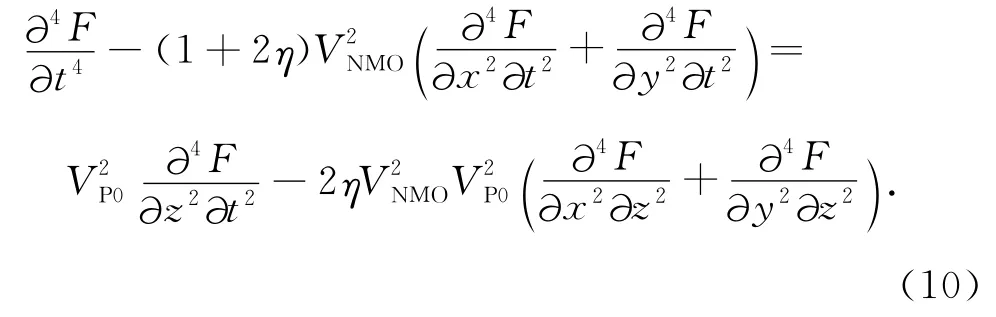
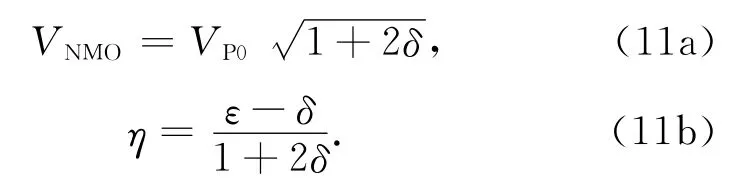
其中VP0为qP波垂直速度，VNMO为NMO速度，η为反椭圆系数，且与Thomsen参数ε与δ存在如下关系：设η=0和VNMO=VP0，（12）式就退化成各向同性介质的程函方程.通过特征值方法可进一步推导出描述射线路径的常微分方程组.为此，将（12）式改写为如下形式：

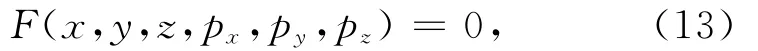
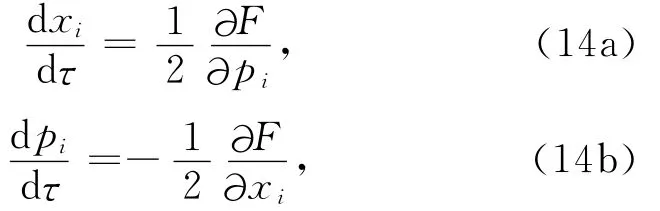
其中，τ代表沿着射线的走时，i对应x，y和z分量.该方程组描述了VTI介质声学近似意义下的射线路径、走时及传播方向信息.可以看出，式（14）与式（9）形式上非常相似，且在算法框架上也基本一致.只不过式（9）在理论上是准确的，而式（14）代表的射线追踪算法存在声学近似引入的误差.

TTI介质与VTI介质并没有物理上的本质区别，若在沿倾斜对称轴的坐标系下考查TTI介质波的传播问题则与VTI介质完全等价.为了推导TTI介质的程函方程，将VTI介质程函方程进行坐标旋转.假设x为标准坐标系，按对称轴的倾角ν与方位角α旋转后的倾斜坐标系记为x′，则坐标变换对应的雅可比矩阵B可以表示成：

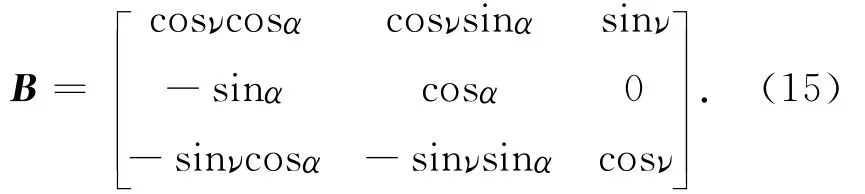
于是由（12）式得到三维TTI介质声学近似意义下的程函方程（见附录B）.设方位角满足α=0，则得到其二维形式：

将（16）式改写为汉密尔顿方程 F（x，y，z，px，py，pz，ν）=0，通过特征值方法仍可将声学近似意义下TTI介质的射线方程表示成（14a）与（14b）的形式.只不过这时对称轴倾角ν也为空间坐标xi的函数，因此（16）式对空间坐标xi求导时，还需对倾角ν求导数.

2.3 两种各向异性射线追踪算法对比

由于局部角度域叠前深度偏移成像算法既需要射线的走时信息，还需要其方向信息，因此在偏移之前按上述原理编写射线追踪算法创建走时与起飞（相）角的数值表.基于国际上通用的二维TTI推覆体模型，对比两种算法的计算精度与效率.如图1（a—d）分别显示了该模型的垂直qP波速度vP0、Thomsen参数ε与δ以及对称轴倾角ν.该模型横向与纵向采样点分别为900和200，采样间隔均为10m.由于声学近似意义下的射线追踪方程不是完全精确的，因此本文将基于它计算的射线路径、走时和文中另一种精确的各向异性介质射线追踪算法进行对比.图2a与图2b中红色射线路径与走时曲线为相速度表示的射线方程计算结果，而蓝色曲线为声学近似射线方程计算结果.两种结果非常接近，表明声学近似射线追踪算法精度仍然比较高，适用于角度域叠前深度偏移算法中走时与起飞角等相关参数的计算.

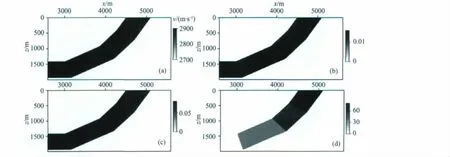
图1 逆冲模型（a）vP0模型；（b）ε模型；（c）δ模型；（d）ν模型.Fig.1 Numerical example on overthrust model（a）vP0model；（b）εmodel；（c）δmodel；（d）νmodel.

图2 局部角度域射线追踪图（a）射线路径；（b）走时曲线图.Fig.2 Local angle domain ray tracing（a）Raypath；（b）Traveltime.

基于同样的模型，表1列出了两种算法在VTI与TTI两种介质情况下计算走时表与起飞角度表所需的CPU时间.对于VTI介质情况，将原TTI介质模型对称轴倾角取为0.从表中可以看出，VTI介质声学近似射线追踪算法效率非常高，但当考虑对称轴倾角时，其计算成本提高了数倍，这主要是因为从VTI介质到TTI介质的坐标变换引入了太多的额外计算量.而基于相速度的射线追踪算法考虑对称轴倾角增加的计算成本不到10%.

表1 两种射线方程计算效率对比Table 1 Computational cost comparison between two ray tracing systems

3 地震波局部角度域成像原理

如果从地下成像点的视角来观察地震波场，成像点处有两种波场，即入射波与散射波（包括反射与绕射波）.在高频渐近意义下，入射和散射波前面分别具有各自的格林函数属性，如走时、几何扩散因子、走时梯度或慢度矢量等.如图3所示，三维情况下，入射慢度矢量ps和散射慢度矢量pr共同描述了散射点m处波的传播方向特征.入射与散射慢度矢量之和pm称为照明矢量.根据地震勘探的需要，可用两类、四个角度共同定义局部传播方向[18］.第一类是描述入射与散射（包括绕射和反射）方向特征的两个角度，即入射角γ（散射张角θ的一半）和散射方位角（即局部入射与散射慢度所在平面的方位角）φ.偏移速度分析、AVA分析／反演就是考察和利用时差或振幅随这两个角度的变化.第二类是描述局部照明方向的两个角度，即照明矢量的倾角ϑ与方位角φ.基于射线理论，这四个角度参数可由走时的空间梯度计算得到[10］.

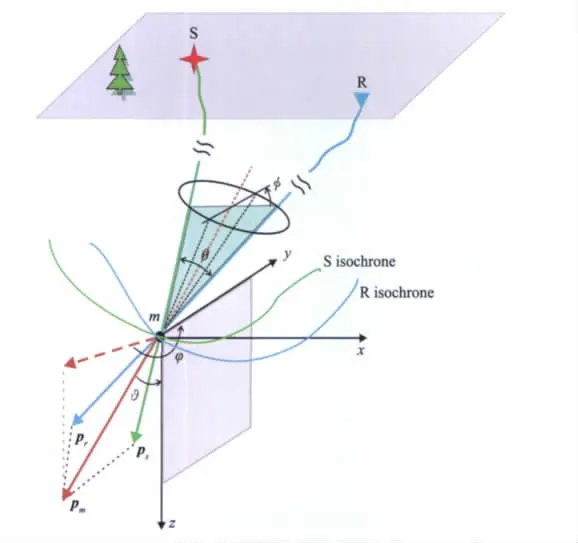
图3 成像点处地震波局部角度特征示意图Fig.3 Local angle characteristics of a selected ray pair at a subsurface image point

设入射射线的起飞角为βs，方位角为αs，散射射线的起飞角为βr，方位角为αr，很容易得入射射线与散射射线的单位慢度矢量：

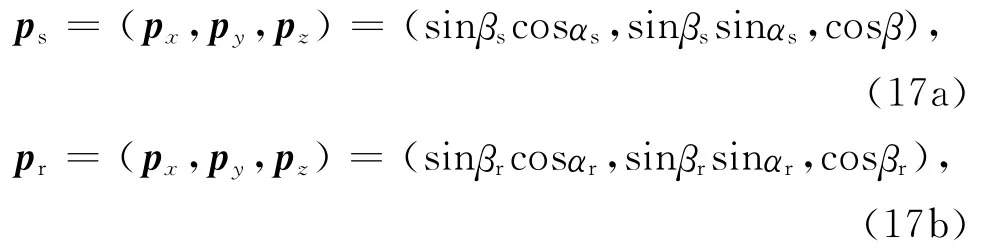
根据矢量运算法则，四个局部角度参数分别满足[10］：

式中x、y与z分别代表沿坐标轴的单位矢量，其中y指向正北方向并作为定义方位角的参考方向，pmz为照明矢量的垂向分量.可见，只要根据起飞角及其方位角计算得到入射与散射慢度矢量，就可根据上述方程求取四个局部角度参数.

在局部角度域进行射线追踪时，从地下成像点以起飞角βs（或βr）与方位角αs（或αr）等间隔向上发射一簇射线到达地表各观测点，将这些不同方向起飞射线的走时与角度信息保存在数值表中.在局部角度域成像时，根据炮点-成像点-接收点关系，在数值表中读取计算好的样本通过插值获得实际射线路径的走时、起飞角及其方位角，进而按公式（17a）至（18d）从射线路径的局部角度参数 （βs，αs；βr，αr）转换成局部角度域成像需要的角度参数（φ，γ；φ，ϑ）.

根据Kirchhoff积分偏移原理，地面观测地震记录各个时刻振幅所对应的偏移脉冲响应按空间位置叠加起来就得到地下构造图像.事实上，脉冲响应曲面任意一点都与可能的特定射线路径相对应，且在各点都具有其局部角度属性.常规的成像结果相当于不同传播方向波场成像值的某种平均，而局部角度域成像就是要在叠前偏移过程中保留这些像的局部方向信息.为了降低计算成本，一般在完全叠加成像数据与炮检距域共成像点道集之外，仅额外输出入射角度（φ，γ）域或者照明角度（φ，ϑ）域的共成像点道集.入射角度域共成像点道集适用于偏移速度分析、成像振幅随入射角或方位角变化（AVA／AVAZ）分析.照明角度域共成像点道集可用于提取地层走向与倾角属性，也可用于绕射波的分离与成像等[10］.

根据Bleistein等[8］的建议，本文把三维入射角度域Kirchhoff叠前深度偏移成像公式写成：

其中I（x，γ，φ）为入射角度域成像结果，A（x，xs）与A（x，xr）分别对应入射波与反射波格林函数中的振幅项，W（x，xr，xr）为与该成像点处的覆盖次数成反比的加权系数，D（x，xr，xr）为滤波后的地震数据，其表达式为

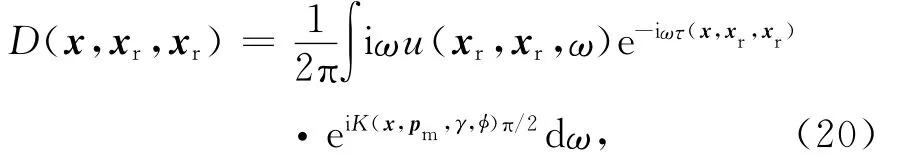
式中u（xr，xr，ω）表示地表观测数据，τ（x，xr，xr）为入射射线与散射射线走时之和，K（x，pm，γ，φ）为KMAH参数，它代表射线经过焦散处引起相位反转的次数.振幅系数A（x，xs）与A（x，xr）以及 KMAH参数通常需由动力学射线追踪得到.为降低计算成本，本文数值算法中的振幅系数采用了均匀介质或横向均匀介质格林函数振幅来替代.如果不考虑随入射方位角的变化，可将（19）式改写为：

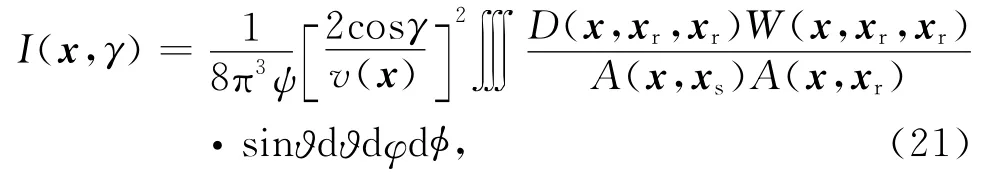
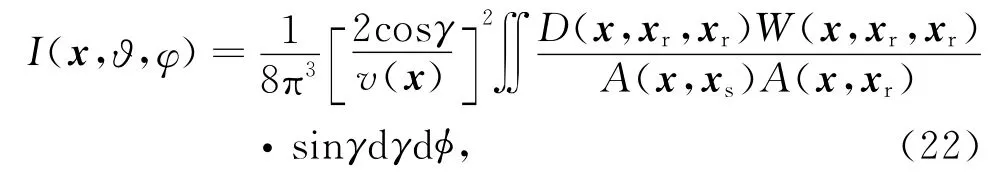
其中，I（x，ϑ，φ）为照明角度域成像结果.

4 数值算例

4.1 SEG／HESS VTI模型

图4（a、b、c）展示了SEG／HESS二维VTI模型垂直qP波速度、Thomsen参数ε和δ.模型左边有一个被各向异性岩层包围的盐丘，右侧为一个断层面，盐丘两侧与断层较为陡峭.射线走时与局部角度计算采用VTI介质声学近似射线追踪算法.图4d为本文VTI介质Kirchhoff叠前深度偏移结果，盐丘边缘与断层都得到了很好的聚焦成像；克服了各向同性介质Kirchhoff叠前深度偏移（图4e）中反射归位不准、绕射未完全收敛、能量不聚焦等问题.图5a展示了该模型偏移后的平均入射角域共成像点道集，其中入射角范围为0°～60°.与传统的偏移距域共成像点道集（图5b）相比，角度域共成像点道集能量更聚焦，波形拉伸效应的影响也弱得多.类似地，图5c与图5d分别展示了忽略各向异性影响的情况下得到的入射角域与偏移距域共成像点道集.可以看出，这两种成像道集大多数同相轴均未拉平，都有上翘的现象.借助这些剩余曲率信息便能够进行各向异性偏移速度分析.

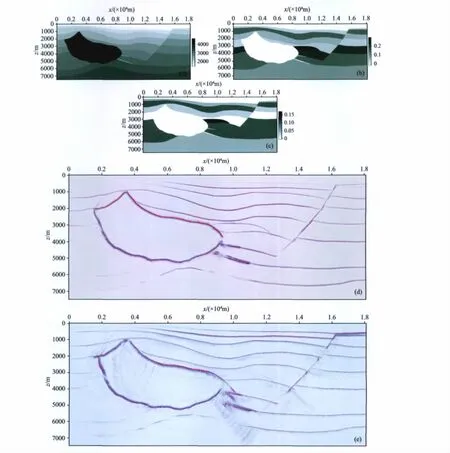
图4 SEG／HESS VTI模型数值算例（a）vP0模型；（b）ε模型；（c）δ模型；（d）考虑各向异性偏移结果；（e）忽略各向异性偏移结果.Fig.4 Numerical example on SEG／HESS VTI model（a）vP0model；（b）εmodel；（c）δmodel；（d）Considered the effects of anisotropy；（e）Ignored the effects of anisotropy.

4.2 TTI逆冲模型

下面以国际上通用的逆冲模型（图1）为例，测试TTI介质局部角度域叠前深度偏移成像算法.该模型数据正演模拟时底部放有一水平反射界面用于测试上覆各向异性介质对该界面反射地震波传播与成像的影响.射线走时与局部角度计算采用前文介绍的相速度表征的TTI介质射线追踪算法.首先对合成数据进行VTI介质Kirchhoff叠前深度偏移（图6a），发现由于忽略对称轴倾角给走时计算带来明显误差，进而导致该反射界面未能准确成像.图6b显示了TTI介质Kirchhoff叠前深度偏移结果，此时底部的水平界面得到了正确成像，观测孔径限制引起的未完全收敛与叠加掉的绕射能量也减弱了许多.图6c为TTI介质局部角度域Kirchhoff叠前深度偏移成像获得的平均入射角域共成像点道集.由于合成数据偏移距范围较小，考虑的入射角范围为0°～25°.图6d展示了TTI介质局部角度域Kirchhoff叠前深度偏移成像获得的照明倾角域共成像点道集.可见，偏移后的反射波为似双曲线形状，其中能量最强的顶点所对应的照明倾角与反射界面的倾角一致，而偏移后的绕射波则具有明显不同的形态.关于照明角度域共成像点道集物理含义和实际用途的讨论可参见文献[18］，[9］和[10］.

5 结 论

本文基于改进的射线追踪算法实现了一种面向TI介质的局部角度域叠前深度偏移成像方法.对比研究的两种改进的射线追踪方法为局部角度域成像提供射线的走时与局部方向信息，它们均不再采用刚度系数而是相速度或Thomsen参数来表示各向异性速度模型.其中声学近似射线追踪方法是基于VTI介质声学近似qP波波动方程与程函方程推导的，本文通过坐标旋转将其扩展到了TTI介质.今后可以照此思路推导诸如正交各向异性等更复杂各向异性介质的声学近似射线方程.从推覆体模型数值试验看，声学近似射线追踪算法精度与文中另一种准确的射线追踪算法非常接近，但从计算效率考虑更适合VTI介质.

根据地震波在成像点处的局部方向特征，文中采用局部角度域成像空间的脉冲响应叠加，实现了入射角度域和照明角度域Kirchhoff叠前深度偏移成像算法.文中二维VTI与TTI模型数值试验表明，该算法能够给各向异性偏移速度分析提供强有力的支撑.这种局部角度域成像方法的优点还在于用到了成像孔径内所有波场数据而不是某些按地面炮检距与方位角分选的数据子集，成像振幅更合理地反映了目的层“原位”的随入射角及其方位变化的带限反射系数信息.本文方法与常规Kirchhoff叠前深度偏移一样，在处理多波至、焦散等问题是存在缺陷.基于与本文TI介质运动学射线追踪对应的动力学射线追踪算法，可在本文理论框架下发展局部角度域高斯束偏移成像方法，进而有效地解决多波至与焦散问题，提高在复杂非均匀各向异性介质中的成像精度.这部分工作拟另文介绍.

致 谢 感谢SEG提供文中使用的理论模型数据.

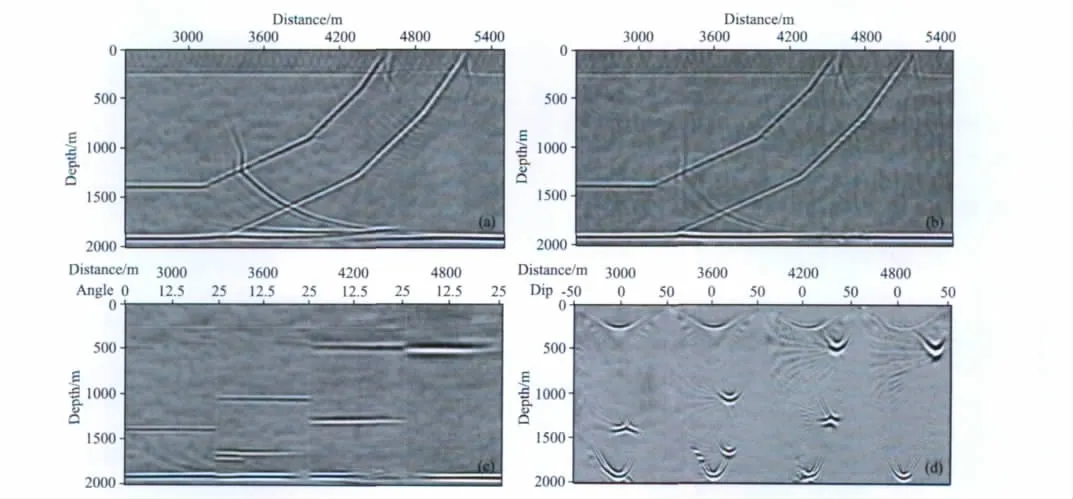
图6 逆冲模型偏移结果（a）VTI偏移结果；（b）TTI偏移结果；（c）平均入射角域共成像点道集；（d）照明倾角域共成像点道集.Fig.6 TTI data migration results（a）VTI migration；（b）TTI migration；（c）Average incident-angle CIGs；（d）Illumination-dip domain CIGs.

附录A 相速度表示的TI介质射线追踪方程

前文给出了Zhu等[15-16］提出的相速度表示的一般各向异性介质的射线方程.在VTI与TTI介质中的具体形式，根据前文，有如下各向异性射线追踪方程组：

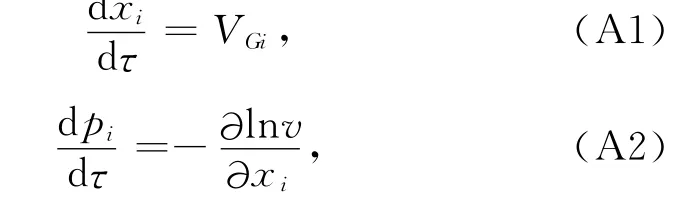
其中群速度可由相速度表示[19］，

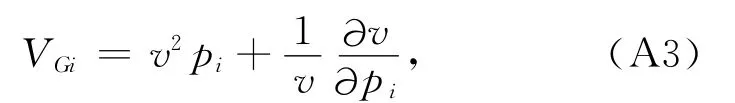
而VTI介质相速度满足[19］：

当TI介质对称轴与垂向存在夹角为ν时，相速度满足：

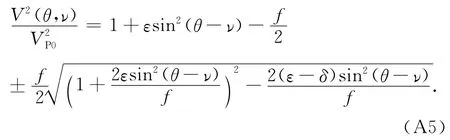
于是在（A1）中采用这种适用于TTI介质的相速度公式即可.如果令相速度公式中的f=1，上述射线方程也就退化成声学近似形式.

附录B：TTI介质声学近似程函方程

TTI介质声学近似意义下的程函方程有如下形式：

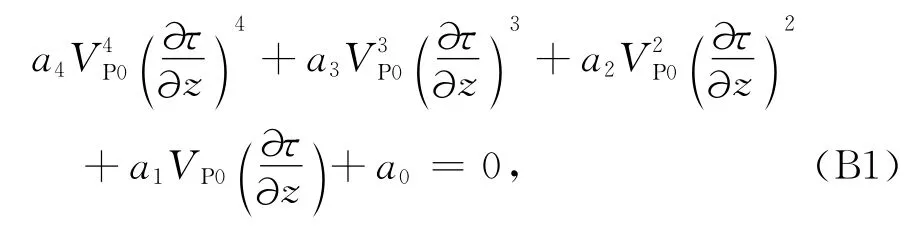
其中，

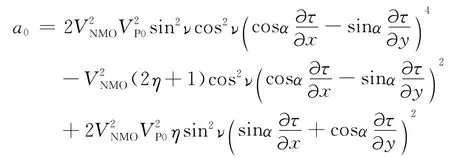
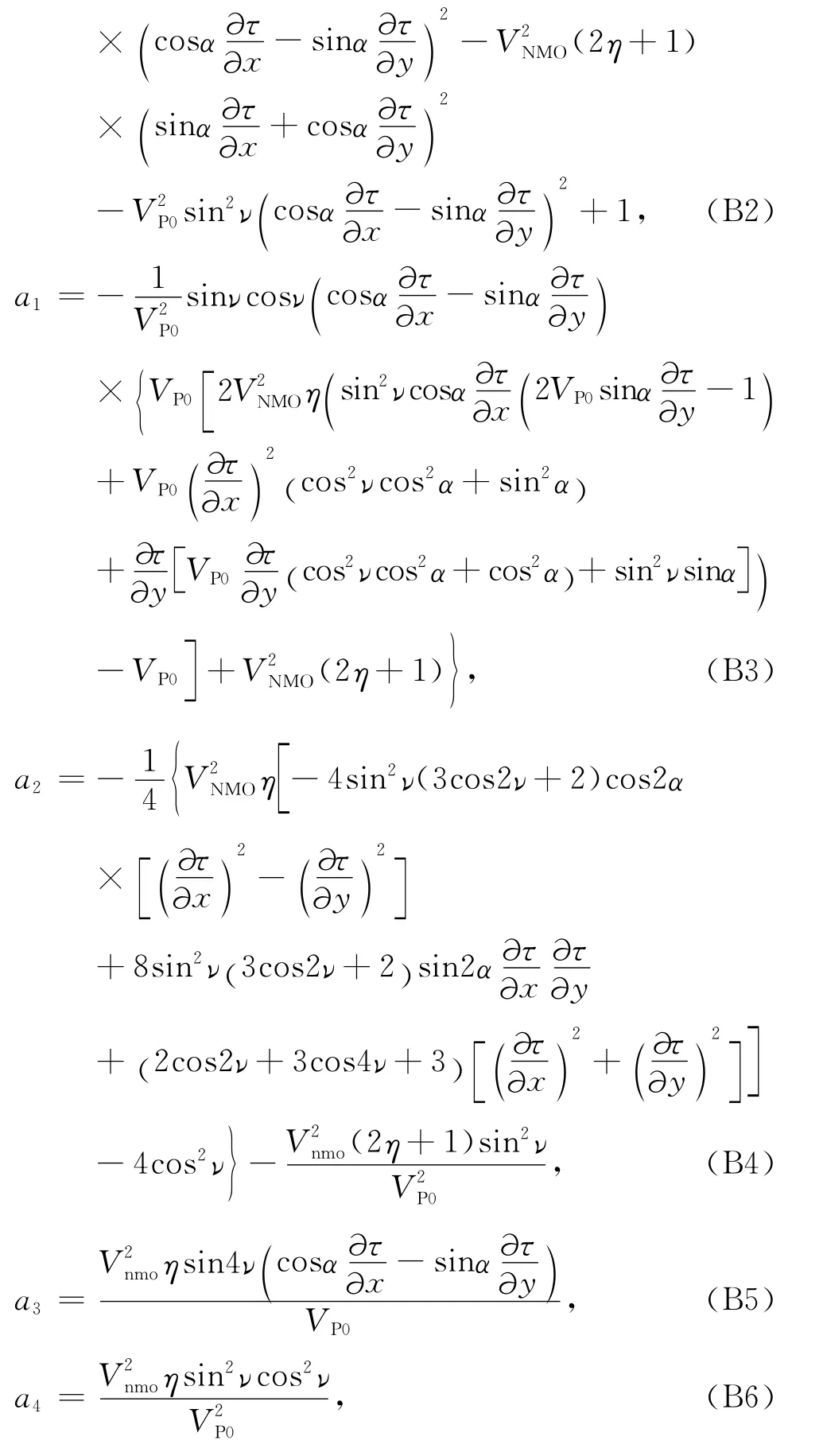
（References）

[1]Kumar D，Sen M K，Ferguson R J.Traveltime calculation and prestack depth migration in tilted transversely isotropic media.Geophysics，2004，69（1）：37-44.

[2]Zhu T F，Gray S H，Wang D L.Prestack Gaussian-beam depth migration in anisotropic media.Geophysics，2007，72（3）：S133-S13.

[3]吴国忱.各向异性介质地震波传播与成像.东营：中国石油大学出版社，2005.Wu G C.Seismic Wave Propagation and Imaging in Anisotropic Medium （in Chinese）.Dongying：China Petroleum University Press，2005.

[4]康玮，程玖兵.横向各向同性介质拟声波方程及其在逆时偏移中的应用.地球物理学报，2012，55（3）：1033-1045.Kang W，Cheng J B.Pseudo-acoustic wave equations for reverse-time migration in TI media.Chinese J.Geophys.（in Chinese），2012，55（3）：1033-1045.

[5]de Hoop M V，Bleistein N.Generalized radon transform inversions for reflectivity in anisotropic elastic media.Inverse Problems，1997，13（3）：669-690.

[6]Xu S，Chauris H，Lambaré G，et al.Common-angle migration：A strategy for imaging complex media.Geophysics，2001，66（6）：1877-1894.

[7]Brandsberg-Dahl S，Ursin B，de Hoop M V.Seismic velocity analysis in the scattering angle／azimuth domain.Geophysical Prospecting，2003，51（4）：295-314.

[8]Bleistein N，Gray S H.A proposal for common-openingangle migration／inversion.Center for Wave Phenomena，Colorado School of Mines.Research Report CWP-420，2002.

[9]Koren Z，Ravve I，Ragoza E，et al.Full-azimuth angle domain imaging.SEG Technical Program Expanded Abstracts，2008：2221-2225.

[10]Cheng J B，Wang T F，Wang C L，et al.Azimuth-preserved local angle-domain prestack time migration in isotropic，vertical transversely isotropic and azimuthally anisotropic media.Geophysics，2012，77（2）：S51-S64.

[11]Vidale J E.Finite-difference calculation of traveltimes in three dimensions.Geophysics，1990，55（5）：521-526.

[12]Schneider W A，Ranzinger K A，Balch A H，et al.A dynamic programming approach to first-arrival traveitlme computation in media with arbitrarily distributed velocities.Geophysics，1992，57（1）：39-50.

[13]Farra V.Ray tracing in complex media.Journal of Applied Geophysics，1993，30（1-2）：55-73.

[14]Cerveny V.Seismic Ray Theory.Cambridge：Cambridge University Press，2001.

[15]Zhu T F，Gray S H，Wang D.Kinematic and dynamic raytracing in anisotropic media-aphase-velocity formulation.Theory and application：75th Annual International Meeting，SEG，ExpandedAbstracts，2005，96-99.

[16]Zhu T F，Gray S H，Wang D L.Prestack gaussian-beam depth migration in anisotropic media.Geophysics，2007，72（3）：S133-S138.

[17]Alkhalifah T.An acoustic wave equation for anisotropic media.Geophysics，2000，65（4）：1239-1250.

[18]Audebert F，Froidevaux P，Racotoarisoa H，et al.Insights into migration in the angle domain.SEG Technical Program Expanded Abstracts，2002：1188-1191.

[19]Tsvankin I.Seismic Signatures and Analysis of Reflection Data in Anisotropic Media.New York：Elsevier，2001.