基于BFGS法融合InSAR和GPS技术监测地表三维形变
2013-09-22李志伟朱建军丁晓利汪长城冯光财
胡 俊,李志伟*,朱建军,丁晓利,2,汪长城,冯光财,孙 倩
1 中南大学 地 球科学与信息物理学院,长沙 410083
2 香港理工大学土地测量与地理资讯学系,香港九龙
1 引 言
InSAR由于其覆盖范围大、空间分辨率高、测量精度高等优势,近年来已经被广泛用于监测地表形变[1].但是其缺点是容易受到大气[2]和失相关[3]的影响,时间分辨率低(几天到几十天,基于卫星的重返周期),并且只能监测地表在雷达视线方向(LOS)上的一维形变[4-7].GPS技术是目前最常用的监测地表形变的方法之一,通过区域布设的GPS网来连续测量,能够提供高精度和高时间分辨率的地表三维运动信息[8].但是GPS较高的安置和运行费用限制了GPS网的密度,因此空间分辨率很低.目前世界上布设密度最大的GPS网是美国南加州的SCIGN网和日本的GEONET网,分辨率也分别只有10~25km和25km左右.InSAR和GPS技术的特点正好形成互补,因此可以最大限度的挖掘地表形变等信息[9-12].
针对InSAR和GPS技术的各自优缺点,Gudmundsson等[13]在2002年首先提出将这两种形变监测技术进行最优融合,将它们优势互补,获取高空间和时间分辨率的地表三维形变.文中,Gudmundsson建立了InSAR和GPS获取的地表形变量的能量方程,通过Markov随机场理论和模拟退火法得到了冰岛Reykjanes Peninsula地区的地表三维形变场.但模拟退火法计算复杂,有时甚至无法收敛.2006年,Samsonov等则对该方法进行了改进,简化了Gibbs能量方程,并对其求偏导得到地表三维形变速率的解析解[14].随后,他利用该解析法获取了美国南加州地区的地表三维形变速率场[15-16].但该方法的缺点是计算时可能会出现数值不稳定的现象.针对此缺点,罗海滨等[17]提出了一种直接分解法,将GPS插值所得的地表水平形变速率作为约束,直接将InSAR的LOS上的形变速率分解成垂直形变速率.该方法虽然简单易操作,但过分依赖于GPS插值所得形变的精度,不能改善地表水平形变精度,对垂直形变精度的提高也有限.
鉴于上述问题,本文提出一种更稳健更实用的综合InSAR和GPS技术监测地表三维形变的方法.该方法是基于文献[14]中改进的综合InSAR和GPS监测地表形变速率的能量函数模型,并将其作为优化反演的目标函数.首先,本文分析了解析法反演该能量函数模型存在的潜在数值不稳定性(病态)问题,指出迭代法是解决数值不稳定性的有效方法之一.其次,对该目标函数进行分析,从理论上证明了它是一个凸二次函数,保证了其局部最优解即为全局最优解.随后,一种有效的局部最优化迭代算法BFGS方法被用来求解地表的三维形变速率场的最优估值.BFGS方法是一种拟Newton法,其特点是具有超线性收敛性和良好的自校正能力[18].因此在本文研究中,该方法即能避免某些全局最优化算法(如模拟退火法)计算复杂且难以收敛的问题,又能巧妙的避开解析法中数值不稳定的现象.最后,本文通过模拟数据和南加州真实数据来验证新方法的可行性和精度.
2 目标函数模型分析
升降轨InSAR干涉图可以提供两个不同LOS方向上的地表形变速率它们与地表在东西、南北和垂直三个正交方向上的形变速率[vxvyvz]T关系如下所示:


其中,α代表雷达方位角,即北方向与雷达的飞行方向的夹角(顺时针),θ代表雷达入射角.
对于GPS而言,它仅提供若干个稀疏点上的地表三维形变速率,因此必须用某种插值方法(如克里金插值法[19])提高其分辨率,得到与InSAR干涉图相同分辨率下的地表三维形变速率:

可以看出,InSAR和GPS都提供了可用来重建地表真实三维形变的信息.根据Gibbs能量方程,可建立如下的能量函数[14]:

可以看出,(4)式中的I1和I2对应于升降轨InSAR,而Gx、Gy和Gz则对应于GPS.建立该能量函数的目的是将其作为参数优化反演的目标函数,即当该函数的能量达到极小时,对应未知参数([vxvyvz]T)的最优结果.对于这个能量函数,Samsonov等提出解析法求解三维形变场,即对U(vx,vy,vz)中的未知量求偏导,并令其均为0,从而归结为一个标准的线性方程组求逆的问题[14]:


值得注意的是,当只有升轨或降轨数据时(即I1=0或I2=0),该能量函数模型也同样适用[15].这种方法虽然简单,但是在实际应用中,可能会带来较大的误差.文献[20]中对这种直接矩阵逆法进行了误差分析,得到其相对误差限为

其中,kcond为矩阵A的条件数,‖Δx‖为解x的误差,‖ΔA‖为系数矩阵A的误差,‖Δb‖ 为常数项b的误差.(6)式表明,x的相对误差受到系数矩阵相对误差、常数项相对误差和条件数的影响.在系数矩阵误差很小的情况下,x的相对误差为b和A的相对误差的kcond倍.因此,如果系数矩阵A是病态矩阵,其条件数kcond很大,那么即使‖Δb‖很小,也有可能会给解x带来很大的影响.而在解析法中,系数矩阵完全有可能是病态的,这一点在后面数据验证时会得证.因此,解析法存在潜在数值不稳定性问题,在病态时将难以获得准确的解.在这种情况下,需要寻找一种不受系数矩阵病态性影响的最优化算法.
迭代法是一种常用的最优化算法,其特点是通过循环计算来无限逼近问题的近似解,不直接对系数矩阵求逆,所以不受其病态性的影响[20].因此,在本研究中,考虑引入迭代算法来解决病态系数矩阵带来的数值不稳定问题.首先对目标能量函数的特性进行进一步分析.分别给出(4)式相应的Hesse阵,以I1为例:

可求得2I1的特征值为
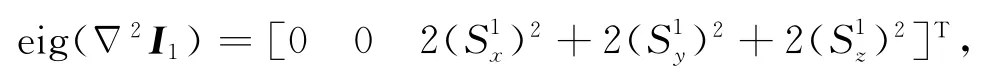
同理可得

可以看出2I1和2I2的特征值均≥0,因此它们在(-∞,+∞)上处处半正定.此外
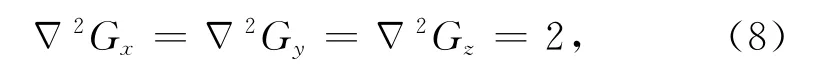
也为 (- ∞,+ ∞)上的正定矩阵.因此,I1、I2、Gx、Gy和Gz均为(-∞,+∞)上的凸函数.由凸函数的性质可知,目标能量函数U(vx,vy,vz)也必为在(-∞,+∞)上的凸函数,其局部最优解即为全局最优解[21].因此,无需设计复杂的全局最优化迭代算法,较为简单的局部最优化迭代算法就可以达到形变速率[vxvyvz]T的全局最优估值.
3 BFGS方法
本研究中,如何设计一种简单有效且适用于前面建立的目标函数的局部最优化迭代算法是一个重点.经过理论研究和实验比较,最终选择了一种目前最流行的、计算性能较好的拟Newton法——BFGS方法.拟Newton法的特点是既继承了Newton法收敛速度快的优点,又克服了Newton法计算量大、产生非下降方向的缺点.而由Broyden、Fletcher、Goldfard和Shanno在1970年提出的BFGS方法则是公认最为有效的拟Newton法,其优势在于在处理实际问题时具有超线性收敛性,并且具有非常好的自校正能力[18].
对于上述改进的综合InSAR和GPS监测地表形变速率的能量函数模型反演优化问题,可以写成如下形式:

式中x∈R3是三维地表形变速率;f:R3→R为目标函数.
BFGS方法开始于以下的迭代过程[18]:

其中,k是迭代次数;αk为步长因子,取为某个满足Wolfe条件的正常数;dk为一个单位矢量,决定下一次搜索的方向,其可由目标函数f(x)的梯度求得:

其中:

其中,I为单位矩阵.当给定初始点x0、误差控制限ε和H0后,利用上式进行迭代运算,当‖Δ f(xk)‖ ≤ε时,迭代停止,输出当前的xk即为最优的地表三维形变速率.
一般当f(x)的Hesse阵的逆矩阵存在的情况下,取H0=Δ2f(x0)-1.但是值得注意的是,在本研究中,Δ2f(x0)-1的行列式值非常之小,因此可能会给结果带来不确定性,事实上,这就是造成解析法不稳定的原因[14].幸运的是,由于BFGS方法良好的自校正能力,H0可取为单位矩阵,事实证明这并不会影响最终的结果,并且可以避免数值解算的不稳定性[22].
4 模拟数据验证
本研究在100×100的网格点上模拟了地表10年的三维形变场.为了尽量贴合真实的地表形变情况,设计地表在东西向和南北向发生了匀速形变,而垂直向则作随时间推移的周期性下沉和抬升.其地表三维形变速率场分别如图1(a,b,c)所示.其中,Vx分量和Vy分量分别在东西向和南北向上从-6cm·a-1匀速增加至6cm·a-1;Vz分量则分为下沉、抬升和稳定三个区域,总体跨度从-8cm·a-1到8cm·a-1.

图1 在100×100的网格点上的模拟的地表三维形变速率场(a)东西向;(b)南北向;(c)垂直向.Fig.1 The simulated three-dimensional displacements velocity fields on 100×100grid(a)East-West direction;(b)North-South direction;(c)Up-Down direction.

图2 加噪后的InSAR监测的地表形变速率场(a)升轨;(b)降轨.Fig.2 The surface displacements velocity inferred by InSAR with Gauss noise(a)Ascending;(b)Descending.
在100×100的模拟地表三维形变速率场的网格点上随机选取100个GPS点,提取出每个GPS点上三维形变速率.同样,标准差为1cm和2.5cm的高斯白噪声分别加到GPS点的水平和垂直形变上.利用普通克里金插值法[19],该加噪后的稀疏GPS监测数据被内插至整个100×100的网格点上,以达到和InSAR相同的空间分辨率.图3(a,b,c)显示的是100个GPS点内插所得的地表三维形变速率场[VxVyVz].可以看出,GPS点在图像上不均匀分布,在GPS点较为稀疏的地方,普通克里金方法的插值效果较差,如图像的右下角.此外,由于水平方向上的噪声较小,它们的插值结果也明显好于垂直方向.
在研究中发现,如果升降轨InSAR的相干性非常之好,即其相应地表形变监测标准差σins很小,而GPS观测或插值标准差σgps比较大时,解析法中的法方程系数矩阵就很可能是出现严重病态.例如,当InSAR的相干性达到0.99,而GPS观测或插值标准偏差大于10cm时,σins/σgps<10-4时,这时解析法的单精度解存在很大的误差.图3(g—i)显示了此时解析法的解算结果.可以看出,三个方向上的形变结果都出现了不同程度的偏差,这是因为此时解析法中的系数矩阵为病态矩阵,条件数接近104,因此给结果带来了很大的误差.而本文所提出的新方法则可以很好的抵抗病态矩阵的不良影响,仍然可以得到稳定的高精度结果(如图3(d—f)).

图3 (a)—(c)普通克里金插值法得到的地表三维形变速率场;(d)—(f)BFGS法得到的地表三维形变速率场;(g)—(i)在σins/σgps<10-4情况下解析法得到的地表三维形变速率场.从左至右分别为东西向、南北向和垂直向结果.黑色点代表随机选取的100个GPS观测站.Fig.3 The three-dimensional displacements velocity fields estimated by(a)-(c)ordinary kriging,(d)-(f)BFGS method and (g)- (i)analytical optimization method withσins/σgps < 10-4,respectively.The left row represent the East-West vectors,the middle row the North-South vectors and the right row the Up-Down vectors.The black dots are randomly picked locations of 100GPS stations.

表1 模拟实验中形变速率的RMSE比较(单位:cm·a-1)Table 1 Comparison of the root mean square errors of the displacement velocities derived in the simulated experiments(Units:cm·a-1)
为了定量分析不同方法的结果,本文在表1中给出了它们的均方根误差(RMSE).可以看出,相对于GPS插值法,直接分解法无法改善水平方向上的地表形变监测精度.而本文中所提出的新方法则可以提高东西向上平均39%左右的形变监测精度;垂直向上的形变监测精度提高的最为明显,相比于GPS插值法和直接分解法则分别平均提高了大约96%和75%,这主要是因为升降轨InSAR对于垂直向的形变最为敏感(投影单位矢量为0.935);而在南北向上,新方法难以改善其形变监测精度,这则是由于升降轨InSAR对于南北向上的形变最不敏感造成的(投影单位矢量为±0.095)[23].而在本次模拟实验中,南北向的精度还略微有点降低,这可能是由于引入了InSAR监测噪声的原因,在实际应用中,该误差是可以忽略的.而解析法的精度则明显不令人满意,在三个方向上都出现了较大的偏差,其结果是不可靠的.
5 真实数据验证
在真实数据处理中,由于地面情况非常复杂,解析法存在的潜在数值不稳定性(病态)问题可能出现.例如遇到GPS站点少或分布不均的情况,GPS插值标准差就会急剧增大,使得解析法不一定可以得到合适的解,而BFGS法则可以避免这种情况的发生,保证了最终的解就是高精度、稳定的全局最优解.为了进一步说明,选取了ENVISAT卫星在美国南加州地区获取的二景降轨ASAR影像(见表2)和当地52个GPS连续观测站提供的地表形变监测资料作为研究对象.美国南加州是一个地质活动频繁、地表形变复杂的地区,其地表不仅受到震间应力累积的影响而做水平运动,还由于地下水抽取和灌溉引起季节性的垂直运动[24].

表2 本文所用到的降轨干涉影像对Table 2 The descending interferometric pair used in this study
首先对二景SAR影像进行二轨差分InSAR处理.其中地形相位的影响利用美国本土30m×30m分辨率的SRTM数据进行剔除;为了消除噪音对干涉图的影响,首先采用了距离向2视、方位向10视的多视处理,随后利用改进的Goldstein方法进行滤波[25];为了避免相位缠绕,采用最小费用流法进行解缠处理;大气的影响则可利用MERIS水汽数据减弱[26].最后对干涉图进行相位到形变的转换,并地理编码至WGS 84坐标系下.如图4a所示,整个南加州地表都在向远离卫星的方向运动,其中最严重的区域超过了4cm·a-1.图4b显示的则是该地区的相干图,很明显,除了山区出现了失相关,大部分地区的相干性都非常好,这得益于两景SAR影像之间较短的空间基线和南加州干燥的气候.通过该相干图和视数,可以得到该形变图的标准偏差[15].
本文研究所用到的52个GPS台站的监测资料由美国南加州综合GPS网(SCIGN)提供.SCIGN网是世界上GPS台站密度最高的网之一,但是在其它的大部分地区,GPS站点的数量都较少且位置分布不均.因此为了使得InSAR和GPS融合监测地表三维形变的方法具有适用性,在本次实验中,只利用其中47个GPS台站(位置见图5中黑色小三角形所示)进行普通克里金插值,而将另外5个GPS站点(位置见图4和图5中黑色小正方形所示)留作最后的检核.从图中可以看出,这5个检验点均位于右下区域,且该区域没有插值点,从而能够检验优化方法在GPS站点分布不均匀的情况下的性能.插值后的东西向、南北向和垂直向形变场分别如图5(a,b,c)所示.其标准偏差可通过 GPS测量标准差和插值标准差计算得到[15].

图4 (a)南加州地区ASAR降轨视线方向上的地表形变速率图;(b)南加州地区的相干图其中底图显示的是SRTM数据提供的当地地形,图中三角形和正方形代表此次研究中所用的52个GPS站的位置.Fig.4 (a)The interferometric displacements velocity map and(b)coherence map of Southern California The shaded relief map of Southern California from SRTM is used as base map.The triangles and squares represent the locations of 52GPS sites used in this study.

图5 (a,b,c)南加州地区GPS插值所得的地表三维形变速率场;(d,e,f)BFGS法所得的地表三维形变速率场;(g,h,i)解析法所得的地表三维形变场从左至右分别为东西向、南北向和垂直向结果.黑色小三角形代表插值用的47个GPS观测站,黑色小正方形代表验证用的5个GPS观测站.P和SFS分别代表Pomona和Santa Fe Springs地区.Fig.5 The three-dimensional displacements velocity fields of Southern California respectively by(a,b,c)ordinary kriging,(d,e,f)BFGS and(g,h,i)Analytical method The left row represent the East-West vectors,the middle row the North-South vectors and the right row the Up-Down vectors.The 47 GPS stations with small black triangles are used for interpolation,while the 5station with small black squares are used for validation.P and SFS represent the Pomona and the Santa Fe Springs areas,respectively.
随后,分别采用BFGS法和解析法对InSAR和GPS形变结果进行最优融合,得到优化后的地表三维形变速率场.在计算中,为了能够得到更为精确的地表三维形变结果,利用了InSAR形变结果中每个像素的雷达方位角和入射角信息来获取该像素的雷达视线方向的单位投影矢量.图5(d,e,f)给出的是BFGS法的结果.从图中可以看出,与GPS插值法相比,BFGS法虽然对水平向上的插值结果改进不大,但在垂直向上则有明显的改善,许多在插值结果中捕捉不到的小区域形变被展示出来.如图5f中的红色圆圈所示,在Pomona地区,大约3cm的地面沉降被BFGS法探测出来;而在Santa Fe Springs地区,则发现了1cm左右地表抬升.这些结果与已有的研究很吻合[27],前者是由于地下水抽取造成的,而后者则是受到油气回灌的作用.然而,GPS插值法却无法反映出来(图5c).这主要是由于ENVISAT卫星入射角较小(约23°),使得InSAR监测对垂直形变更加敏感.此外,缺乏升轨数据也可能是水平结果改进不大的原因之一.图5(g,h,i)显示的则是解析法的结果,可以看出三个方向的形变图在右下角位置都出现了明显的不连续的异常形变(如蓝色矩形框所示),与已有的研究完全不符[26-27],因此是错误的.这是由于在这个区域GPS插值标准差过大引起的系数矩阵病态问题,从而导致该区域形变结果不稳定.然而,BFGS法的结果则非常稳定(图5(d,e,f)).
由于无法获取其它手段得到的地表形变场来验证最终的结果,因此本文采用BLSA等5个站点上的GPS测量结果与InSAR/GPS融合结果进行比较.如表3所示,解析法在东西、南北和垂直向上的形变都与GPS测量结果出现了很大程度的偏差,其结果是不可靠的,这与模拟数据得出的结论是一致的;而新方法在三个方向上的结果都与GPS测量值非常吻合,且比GPS插值法和直接分解法的精度都有了一定的提高.但是,由于被用来验证的5个GPS点本身的形变量比较小(不在形变明显的区域),而且GPS观测值本身也存在一定误差,特别是垂直向的结果精度较差,一般为水平向结果精度的2~3倍,因此相比其它方法,新方法的改善程度没有模拟实验中那么显著.
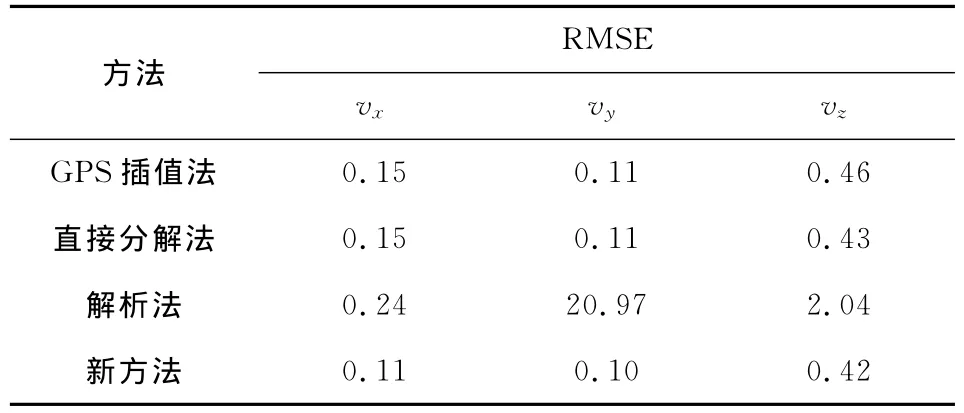
表3 南加州地区实验中不同方法得到的形变速率的RMSE比较(单位:cm·a-1)Table 3 Comparison of the root mean square errors of the displacements velocities derived from different methods in the Southern California experiments(Units:cm·a-1)
6 结 论
为了提高地表三维形变监测的时空分辨率和精度,国内外许多学者将InSAR技术和GPS技术进行融合,以求优势互补.本文在已有研究的基础上,对综合InSAR和GPS监测地表形变速率的能量函数模型进行深入分析和研究,针对目前常用的解析法存在的潜在数值不稳定性(病态)问题,指出迭代法更适合用于模型的反演;并从数学上证明了一种局部最优化算法就能够得到该能量函数模型全局最优解,因此无需引入复杂的全局最优化算法.随后,本文引入BFGS局部最优算法对该目标函数模型进行优化反演.
相比于复杂的全局最优化算法,BFGS方法计算简单且具有超线性收敛性,仅需要几次迭代就可以达到全局最优解;另一方面,BFGS方法良好的自校正能力使其在计算中可利用单位矩阵替代Hesse阵的逆矩阵,从而避免了解析法在计算过程中由于矩阵近似奇异而带来的数值不稳定现象.模拟和真实试验结果表明,在GPS站点较少或分布不均造成GPS插值标准差过大的情况,解析法往往会带来不稳定性,从而大大降低了解的精度;而BFGS方法则不受GPS数量和分布的影响,能够得到最优的地表三维形变估值,且精度优于插值法和直接分解法.致 谢 本次研究所用的ENVISAT ASAR数据为欧洲空间局(ESA)提供(AO-4458,4914);GPS数据由美国南加州综合GPS网(SCIGN)所提供(http://www.scign.org/),在此一并表示感谢.
(References)
[1]Massonnet D,Feigl K J.Radar interferometry and its application to Changes in the Earth′s surface.Reviews of Geophysics,1998,36(4):441-500.
[2]Li Z W,Ding X L,Huang C,et al.Atmospheric effects on repeat-pass InSAR measurements over Shanghai region.Journal of Atmospheric Solar-Terrestrial Physics,2007,69(12):1344-1356.
[3]Zebker H A,Villasenor J.Decorrelation in interferometric radar echoes.IEEE Transactions on Geoscience and Remote Sensing,1992,30(5):950-959.
[4]Ding X L,Liu G X,Li Z W,et al.Ground Subsidence Monitoring in Hong Kong with Satellite SAR Interferometry.Photogrammetric Engineering and Remote Sensing,2004,70(10):1151-1156.
[5]Lu Z,Masterlark T,Dzusisin D,et al.Magma supply dynamics at westdahl volcano,alaska,modeled from satellite radar interferometry.Journal of Geophysical Research,2003,108(B7):2354,doi:10.1029/2002JB002311.
[6]王超,张红,刘智等.基于D-InSAR的1993—1995年苏州市地面沉降监测.地球物理学报,2002,45(增刊I):244-253.Wang C,Zhang H,Liu Z,et al.Subsidence of Suzhou city(China)from 1993to 1995detected by ERS differential SAR interferometry.Chinese J.Geophys.(in Chinese),2002,45(Suppl.I):244-253.
[7]Hu J,Li Z W,Ding X L,et al.Two-dimensional Co-Seismic surface displacements field of the Chi-Chi earthquake inferred from SAR image matching.Sensors,2008,8(10):6484-6495.
[8]Zhu J J,Santerre R,Chang X W.A bayesian method for linear,inequality-constrained adjustment and its application to GPS positioning.Journal of Geodesy,2005,78(9):528-534.
[9]Sudhaus H,Jónsson S.Improved source modelling through combined use of InSAR and GPS under consideration of correlated data errors:application to the June 2000Kleifarvatn earthquake,Iceland.Geophysical Journal International,2009,176(2):389-404.
[10]万永革,沈正康,王敏等.根据GPS和InSAR数据反演2001年昆仑山口西地震同震破裂分布.地球物理学报,2008,51(4):1074-1084.Wan Y G,Shen Z K,Wang M,et al.Coseismic slip distribution of the 2001Kunlun mountain pass west earthquake constrained using GPS and InSAR data.Chinese J.Geophys.(in Chinese),2008,51(4):1074-1084.
[11]张勤,赵超英,丁晓利等.利用GPS与InSAR研究西安现今地面沉降与地裂缝时空演化特征.地球物理学报,2009,52(5):1214-1222.Zhang Q,Zhao C Y,Ding X L,et al.Research on recent characteristics of spatio-temporal evolution and mechanism of Xi'an land subsidence and ground fissure by using GPS and InSAR techniques.Chinese J.Geophys.(in Chinese),2009,52(5):1214-1222.
[12]陈国浒,单新建,Wooil M等.基于InSAR、GPS形变场的长白山地区火山岩浆囊参数模拟研究.地球物理学报,2008,51(4):1085-1092.Chen G H,Shan X J,Wooil M,et al.A modeling of the magma chamber beneath the Changbai Mountains volcanic area constrained by InSAR and GPS derived deformation.Chinese J.Geophys.(in Chinese):2008,51(4):1085-1092.
[13]Gudmundsson S,Sigmundsson F,Carstensen J M.Three-Dimensional surface motion maps estimated from combined interferometric synthetic aperture radar and GPS data.Journal of Geophysical Research,2002,107(B10):2250,doi:10.1029/2001JB000283.
[14]Samsonov S V,Tiampo K F.Analytical optimization of a DInSAR and GPS dataset for derivation of three-dimensional surface motion.IEEE Geoscience and Remote Sensing Letters,2006,3(1):107-111.
[15]Samsonov S V,Tiampo K F,Rundle J B,et al.Application of DInSAR-GPS optimization for derivation of fine-scale surface motion maps of southern California.IEEE Transcations on Geosciences and Remote Sensing,2007,45(2):512-521.
[16]Samsonov S V,Tiampo K F,Rundle J B.Application of DInSAR-GPS optimization for derivation of three-dimensional surface motion of the southern California region along the san andreas fault.Computers &Geosciences,2008,34(5):503-514.
[17]罗海滨,何秀凤,刘焱雄.利用DInSAR和GPS综合方法估计地表3维形变速率.测绘学报,2008,37(2):960-963.Luo H B,He X F,Liu Y X.Estimation of three-dimensional surface motion velocities using integration of DInSAR and GPS.Acta Geodaetica et Cartographica Sinica (in Chinese),2008,37(2):960-963.
[18]董云达.数值优化引论.郑州:黄河水利出版社,2007.Dong Y D.Introduction to the Numerical Optimization(in Chinese).Zhengzhou:Yellow River Conservancy Press,2007.
[19]张仁铎.空间变异理论及应用.北京:科学出版社,2005.Zhang R Z.Spatial Variability Theory and its Application(in Chinese).Beijing:Science Press,2005.
[20]韩旭里,万中.数值分析与实验.北京:科学出版社,2006.Han X L,Wan Z.Numerical Analysis and Experiments(in Chinese).Beijing:Science Press,2006.
[21]何坚勇.最优化方法.北京:清华大学出版社,2007.He J Y.Optimization Method (in Chinese).Beijing:Tsinghua University Press,2007.
[22]Xu P L.A hybrid global optimization method:the multidimensional case.Journal of Computational and Applied Mathematics,2003,155(2):423-446.
[23]查显杰,傅容珊,戴志阳.DInSAR技术对不同方位形变的敏感性研究.测绘学报,2006,35(2):133-137.Zha X J,Fu R S,Dai Z Y.The sensitivity of DInSAR to surface deformation in different direction.Acta Geodaetica et Cartographica Sinica (in Chinese),2006,35(2):133-137.
[24]Bawden G W,Thatcher W,Stein R S,et al.Tectonic contraction across los angeles after removal of groundwater pumping effects.Nature,2001,412(6849):812-815.
[25]孙倩,朱建军,李志伟等.基于信噪比的InSAR干涉图自适应滤波.测绘学报,2009,38(5):437-442.Sun Q,Zhu J J,Li Z W,et al.A new adaptive INSAR interferogram filter based on SNR.Acta Geodaetica et Cartographica Sinica (in Chinese),2009,38(5):437-442.
[26]许文斌,李志伟,丁晓利等.利用 MERIS水汽数据改正ASAR干涉图中的大气影响.地球物理学报,2010,53(5):1073-1084.Xu W B,Li Z W,Ding X L,et al.Correcting atmospheric effects in ASAR Interferogram with MERIS integrated water vapor data.Chinese J.Geophys.(in Chinese),2010,53(5):1073-1084.
[27]Lanari R,Lundgren P,Manzo M,et al.Satellite radar interferometry time series analysis of surface deformation for the metropolitan los angeles and San Francisco,California,areas.Geophysical Research Letters,2004,31(L23613),doi:10.1029/2004gl021294.
