中尺度涡影响下目的层地震成像的畸变与影响因素分析

姬莉莉，林 缅

中国科学院力学研究所环境力学重点实验室，北京 100190

1 引 言

大量的地震资料分析表明，内波、峰团、中尺度涡等海洋中尺度现象都会反映在地震成像中[1-8］.在这些非均匀的、运动的水体内部，各层海水之间由于温度和盐度的差异会产生波阻抗的差别.海水层间的这种波阻抗的差别会引起地震波多次反射，覆盖了中深层地震数据，增大了从地震波场中提取有效波场的难度.同时，许多观测还发现，超大深度的水体使得地震波到达目标深度时能量严重衰减.这些现象充分说明，由于超大深度水体动力环境的不稳定性，加剧了地震波传播的复杂性.因此，有必要从机理上研究海洋中尺度现象对地震波传播的影响.

20世纪70年代以来，中尺度涡一直是物理海洋学家研究的重点.中尺度涡在海洋中几乎处处存在，根据旋转方向的不同，可分为气旋式和反气旋式两类：气旋涡内的海水做逆时针旋转运动，反气旋涡做顺时针旋转运动.研究表明中尺度涡会引起水声场变化[9-14］.Parker[10］指出中尺度涡的存在可以使等温线提升500m或更多，导致声道轴抬高，特别是在上层水体，中尺度涡对声信号有很明显的干扰.近几年，一门新兴的学科——地震海洋学的研究表明，当水中温度在垂向上变化足够大（每米变化几百分之一度）时，会引起地震反射波速度的变化，就会在地震成像中看到它的反射层[15-17］.Krahmann指出[15］，由于水体中温度的变化，反射波相位的变化能达到180°或更多.Holbrook等在处理地震数据时，发现了清晰的地中海旋涡的地震影像图.从图中可以看出，中尺度涡内反射层密集，且结构复杂.这些研究充分表明，中尺度涡的存在必然对目标地层的成像造成一定的影响.因此从机理上研究中尺度涡影响下目标地层成像的畸变是当务之急.

一般情况下，在地球物理界通常采用波动方程方法和射线追踪方法处理地震成像问题.但是，波动方程方法的计算耗时相当长，不太适应讨论机理问题；射线追踪方法虽然在物理图像的直观理解上很吸引人，但是它建立在高频近似的基础之上.因此本文采用抛物方程（PE）方法[18-21］模拟低频地震波传播.与波动方程方法相比，PE方法的优势在于计算速度更快，占用内存很小；与射线方法相比，PE方法在计算低频传播问题时精度更高.

本文首先介绍旋涡模型和PE方法.之后，模拟自激自收的地震波场并分析中尺度涡群影响下目标地层成像的畸变.最后研究涡强度对目标地层成像的影响，从机理上分析了造成目标地层成像畸变的原因.

2 计算方法

本文建立如图1所示的物理模型.假设含有中尺度涡的海水层为非均匀介质，海底有两层均匀弹性介质.

图1 物理模型Fig.1 Sketch of the physical model

2.1 旋涡模型

本文所用旋涡模型于1977年由Henrick等[11］提出，并经过后人的发展，不断完善[14，22］.假设海水深度为D，笛卡尔坐标以维度φ为中心，x′轴正方向指向正东方，y′轴正方向指向正北方，z′轴从海平面垂直向下.Ω=7.27×10-5s-1是地球的角速度，旋涡中心位于坐标原点.ρ，p，c分别表示海水的密度，压力和声速.v=（u，v，w）表示海水流动的速度，u，v，w 是其在x′，y′，z′轴上的分量.为方便求解，将上述坐标系转化到 （r′，θ′，z′）柱坐标系下，其中r′表示到涡中心的水平距离，θ′表示和x′轴的夹角.无量纲参数见表1.

表1 旋涡模型中无量纲参数Table 1 Non-dimensional variables in the eddy model

设海水密度和压力场分别由静态和旋涡扰动两部分组成：

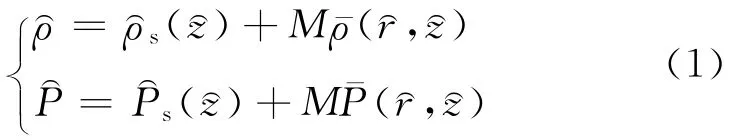
设静态区域的密度和压力只随深度变化，可得

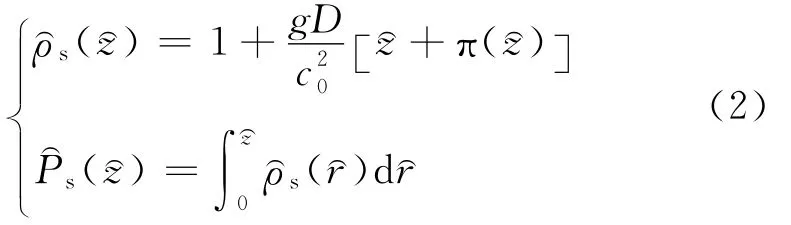
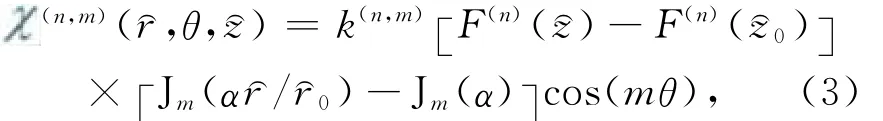
其中Jm为m阶第一类Bessel函数；α为常数，根据实际情况而定；r⌒0和z⌒0为旋涡有效影响半径和影响深度

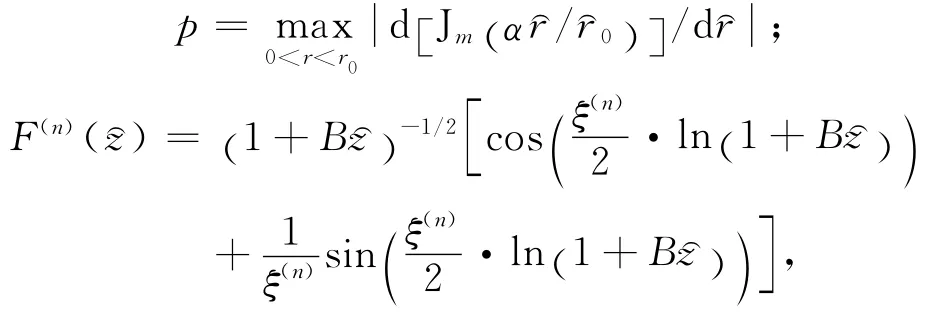
ξ（n）=2nπ／ln（1+Bz0），n=1，2，3，… ，当旋涡为暖（冷）涡时，k（n，m）式中取正（负）号.

于是有：

利用Eckar公式[23］计算旋涡内温度和声速：

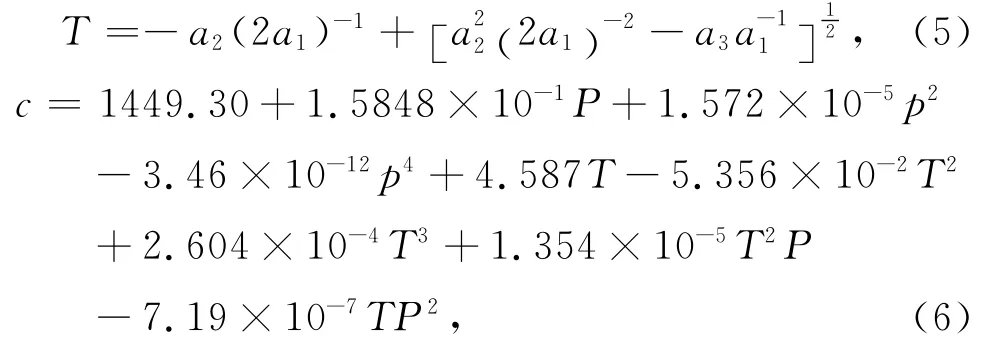
其中，

这样给定旋涡的有效影响半径r0，有效影响深度z0，海水表面最大流速U0，海水表面声速c0，海水表面密度ρ0，合适的常数A，B（由实测的温盐数据确定）以及旋转方向，就可以确定旋涡的流速和声速结构.下面将用此模型并结合实测的CTD数据模拟中尺度涡内的声速.

2.2 PE方法

抛物方程近似方法的基本假设为能量传播的速度接近于一个参考速度——剪切波速度或压缩波速度.基于此假设，将波动方程中的椭圆算子分解为出射波和入射波，忽略后向散射的作用，用抛物算子代替椭圆算子.水中和地层中抛物方程的推导略有不同.在水中，声波满足的质量守恒方程、欧拉方程和绝热状态方程，分别为

其中ρw是海水密度；vw是质点速度；Pw为压强.

假设声源为连续声源，则声压满足：Pw（r，θ，z，t）=pw（r，θ，z）e-ift，其中f 为频率.

为求解方程（7）做如下假设：（a）中尺度涡引起的海水非均匀性为小扰动，即pw=pw0+pw1，ρw=ρw0+ρw1，vw=vw0+vw1其中pw0，ρw0，vw0是静水中的物理量，pw1，ρw1，vw1是扰动量；（b）马赫数 M 为小量δ；（c）垂直方向和水平方向上的特征长度之比为小量；（d）只考虑X轴方向的流速，Z轴方向的流速忽略不计；（e）流体密度、声速和流速只是空间的函数，与时间无关；（f）忽略地震波的后向散射.

本文只考虑二维柱坐标系（r，z）下的情况，其中r是距震源水平方向的距离，z为距离海平面的纵向深度.引入势函数pw1=ψ（r，z）r-1／2eik0r，忽略高阶小量，则方程（7）简化为

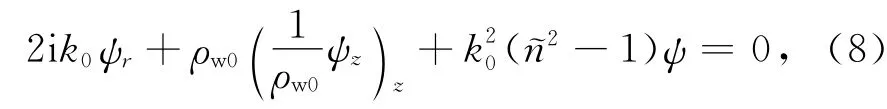
在均匀弹性介质中，只考虑纵波的影响[24］.声波满足的控制方程如下：

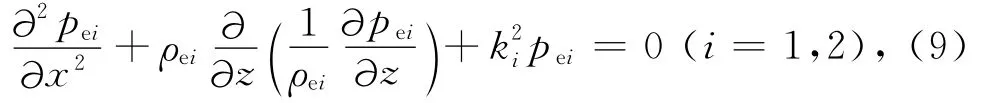
其中，pei为弹性介质的声压，ρei为弹性介质密度，ki为波数.这里下角标i分别表示弹性介质1和弹性介质2.

和水中类似，在均匀弹性介质中也采用PE方法，忽略出射波的后散射作用并在柱坐标系下求解.将方程（9）中的椭圆算子分解成出射波和入射波两个因子的乘积.这里只考虑入射波，并将其做线性Taylor展开，去掉高阶项，可得方程如下：

2.3 边界处理

在海平面，假设海洋表面为释压面：

在交界面上，满足声压连续和法向粒子运动速度连续，即：

这里zb1为水底面，zb2为弹性介质1和弹性介质2的交界面.

在底面，假设底面为完全刚性的，即：

其中，zb3为弹性介质2的底面

初始条件：声源采用广义高斯声源，即在r=0处：

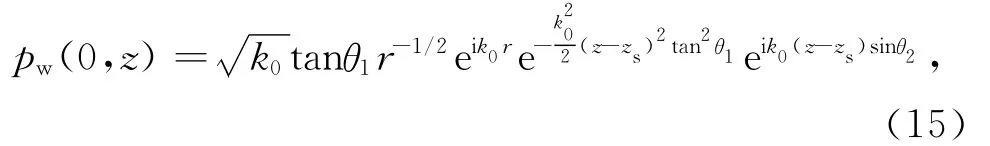
其中，θ1为声源开角的半宽度，θ2为波束相对水平面的倾角，zs为震源的深度.

3 中尺度涡群

实际海洋环境中，中尺度涡往往以多涡形式存在.这里以马尾藻海西南部海域实测的冷涡群（含三个冷涡）为例来考虑中尺度涡群对地震成像的影响.计算模型大小水平方向长800km，纵向深6.0km.声源放置深度为50m.模型仍分为三层：海水层，两层均匀弹性介质.其中海水层的深度为5.0km.由于涡群的存在，海水层在横向和纵向上都具有非均匀性.弹性介质的厚度均为0.5km，弹性介质1中纵波的速度为2km·s-1；弹性介质2中纵波的速度为2.5km·s-1.将实测的温盐数据代入到旋涡模型中，可得含中尺度涡群时水中的声速分布如图2所示.可以看出，涡群的影响范围主要集中在2200m以上，而且涡群内声速的非均匀性很强.

3.1 涡群对地震波场的扰动

为了研究中尺度涡群对目标地层成像的影响，将PE方法和地震数值模拟方法相结合，模拟自激自收的地震波场.之所以选择模拟自激自收的情况，是因为它可以比较直观的反映地层地貌，不用考虑偏移距带来的影响.计算时在800km的海域放置80个声源，间距为10km.这里重点分析中尺度涡群在低频地震勘探中的影响，因此计算了三种低频的情况：10、20Hz和30Hz.图3为有涡群情况下不同频率的地震波场图.这里只给出了连续声源条件下水中的地震波场.

从图3可以看出：地震波场受到的扰动主要集中在海水的上半部分，并且涡内的反射层密集，反射层的结构复杂.这一点与图2的速度模型是吻合的.就不同频率而言，震源频率越大，地震波场受到的扰动越大.

图2 有涡时海水中速度模型Fig.2 Sound-speed model in the sea with eddies

图3 不同频率的地震波场图Fig.3 Seismic wave fields with different frequency

由此可见，涡内部的非均匀性会导致地震波场受到扰动.也即是说，地震勘探中目标地层的反射波会受到涡中反射层的干扰.涡内部非均匀性越强，反射波受到的干扰越大；震源频率越大，反射波受到的干扰越大.

3.2 涡群对目标地层成像的影响

为了更好地观察中尺度涡群对目标地层成像的影响，将第二层弹性介质改为台阶形，计算自激自收情况下检波器接收到的声压.台阶的高度为250m.为了便于比较，将有涡和无涡时得到的台阶地层反射波的声压绘制在一张图上（见图4）.同样考虑了上述三种频率.为了便于定量地研究涡群对目标地层成像的影响，这里引入地形畸变率的概念.所谓地形畸变率是指在自激自收情况下有涡时台阶地层反射波的声压幅值相对于没有涡时声压幅值的变化率.这里需要指出的是地形畸变率都为正值，如果是负向变化则取绝对值.

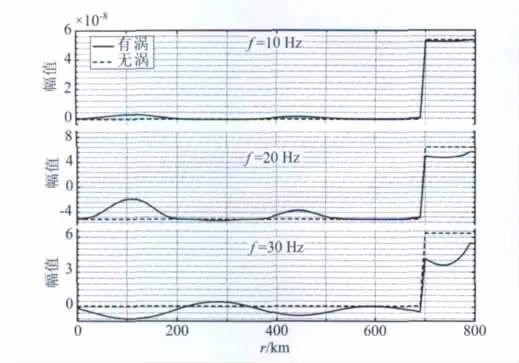
图4 有涡和无涡时台阶地层反射波声压幅值的对比Fig.4 Comparison of pressures caused by reflected wave of the step between through the eddy field and noeddy case for different frequencies

从图4可以看出，没有涡时检波器接收到的声压完全反映了目标地层的台阶结构（虚线）.但当有涡时得到的地层结构就会发生弯曲，与实际不符，而且出现结构畸变的区域基本上就和三个涡的分布大致一致.首先，就同一频率而言，在有涡群的情况下，地形的畸变会出现三个大的峰值，这三个峰值的位置分别对应于三个涡的中心.其次，由图2可知涡群中各个涡之间的界限并不明显，反映在地震成像中就是地形的崎岖是连绵不断的，不规则的.甚至于在第一个涡与第二个涡之间还会出现地形畸变的小的峰值.这说明由涡和涡之间的相互作用所产生的反射层对地震成像的影响也是不容忽略的.再者，就不同频率而言，由于旋涡扰动产生的结构起伏随着频率的升高而变大.这一点和地震波场的计算是吻合的.

综上所述，涡群对目标地层成像会起到干扰作用，使得真实的地层结构无法在地震成像中确切地反映.实际上这一点在地震海洋学中也有反映.Hunt等[25］分析红海的低频反射地震剖面时就发现，由于红海热盐异常水体的存在，使得海底构造在地震剖面中无法准确确定.

3.3 不同深度涡群对目标地层成像影响的比较

为了考虑不同海水深度情况下目标地层成像的畸变，选取两种水深：2500m和5000m，分别在10Hz、20Hz情况下计算台阶地层反射波的声压.

从图5可以看出，深度为5000m的时候，目标地层成像的畸变较大.例如：在第二个涡中心处，20Hz时2500m的地形畸变率为6.11%，5000m的地形畸变率为14.9%；10Hz时2500m的地形畸变率为0.43%，5000m的地形畸变率为3.4%.随着深度的增加，目标地层成像的畸变也增大.这说明，在地震勘探中，海水越深，旋涡的影响越是不可以忽略.

4 涡强度对目标地层成像的影响

由以上计算结果可知，目标地层成像的畸变随涡强度的变化而变化，而且涡中心引起的地形畸变率最大，因此为了考察涡强度对目标地层成像的影响，以南海恒春西南海域实测的单个暖涡为例，计算涡中心处的最大地形畸变率.

计算模型如下：水平方向400km，纵向深2.64km.模型分为三层：海水层，两层均匀弹性介质.其中海水层的深度为2.2km.涡的有效影响深度为1.6km，涡的中心位于200km处；假设地层为均匀弹性介质，且第二层弹性介质为台阶形，台阶高度为110m.震源的频率都为25Hz.

根据涡强度的定义，考察旋涡最大流速U0和有效影响半径r0两个物理量.分别取最大流速为2.0、1.0、0.1、0.01m·s-1，有效影响半径取50、75、100km、125、150、175km.图6绘出了涡中心的声速剖面和不同有效影响半径r0下最大地形畸变率随流速变化曲线.可以看出，暖涡使得声道轴降低，而最大地形畸变率随着流速的增大而增大.当流速为从0.01m·s-1升至2.0m·s-1时，声道轴降低了约300m，畸变率则从5.27×10-4升至0.29.这个结果表明，涡强度越大，声速梯度越大，旋涡内就越容易产生复杂的反射层，因此目标地层成像的畸变也就越大.

拟合图6中地形畸变率的各条曲线，发现最大地形畸变率ΔDmax与旋涡的有效影响半径r0和最大流速U0存在如下的定量关系：

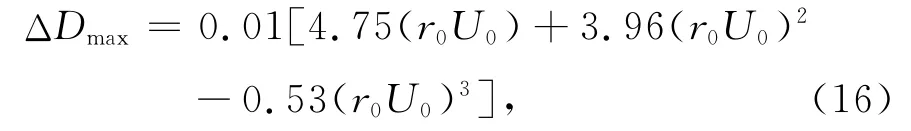
其中r0的单位为：百千米.那么，对于给定r0和U0的旋涡，就可以确定最大地形畸变率.需要注意的是，这个公式仅适用于前面所给出的实测单涡且震源频率为25Hz的情况.为了和一般意义上的涡强度相区别，这里定义r0U0为旋涡的有效涡强度，用γ表示（单位：100km·m·s-1）.

5 畸变机理分析

以第4节中的单涡模型为例分析造成目标地层成像畸变的机理.选取涡的有效影响半径为150km，最大流速分别为1.0、0.1、0.01m·s-1，即旋涡的有效涡强度γ分别为1.5，0.15、0.015.考虑200km区域之内的地形畸变率（半个旋涡的范围）.根据地形畸变率的大小，分三个区间讨论（60～70km，80～90km，100～200km）.对于同一涡强度而言，在相同区间内，地形畸变率的大小差别不大，因此就取各个区间内的平均地形畸变率来讨论问题（这里所谓平均地形畸变率是指该区间地形畸变率的平均值）.表2给出了不同区间平均畸变率随有效涡强度的变化.

表2 不同有效涡强度情况下平均地形畸变率Table 2 The average distorted rate for different effective intensity of eddies

很明显，对于同一有效涡强度而言，不同区间的地形畸变率差别较大.为了解释畸变机理，给出了最大流速为1.0m·s-1（即有效涡强度为1.5）时温度差的等值线图（见图7a），这里所说的温度差是指在同一地点有涡和没有涡时温度的差值，即旋涡引起的温度扰动值.由于所用模型是暖涡，所以温度差都为正值，如果为冷涡，则取两者之差的绝对值，以保证温度差为正.可以看出，在水深小于1000m时，4个区间的温度差相差近一个量级，与相应的平均地形畸变率相对应.从不同有效涡强度的角度来看（见图7b），这里仅比较1000m水深范围内最大流速为1.0m·s-1（虚线）和0.01m·s-1（实线）的温度差.在100～200km的区间内，最大流速1.0m·s-1和0.01m·s-1之间的温度差值相差了两个量级，正好与表2中的平均地形畸变率相对应.再者，最大流速为1.0m·s-1时小于60km的区间（见图7（a））和最大流速为0.01m·s-1时小于100km的区间（见图7b）温度差都小于0.01°，而由表2可知这些区域的平均地形畸变率都小于10-4.地震海洋学的研究表明，水层中温度变化小于百分之一度时，在地震图像中就看不到它的反射层，也就是说，此时水层对地震波的反射可以忽略.我们的计算结果恰好验证了这一结论.

以上研究表明，中尺度涡所带来的温度变化是造成地震成像畸变的一个重要因素.同理，可认为中尺度涡对目标地层成像的影响在一定程度上可以由温度差来确定.至于中尺度涡其他参数的影响还有待进一步的研究.

由涡模型中的公式（1）和公式（4）可得：

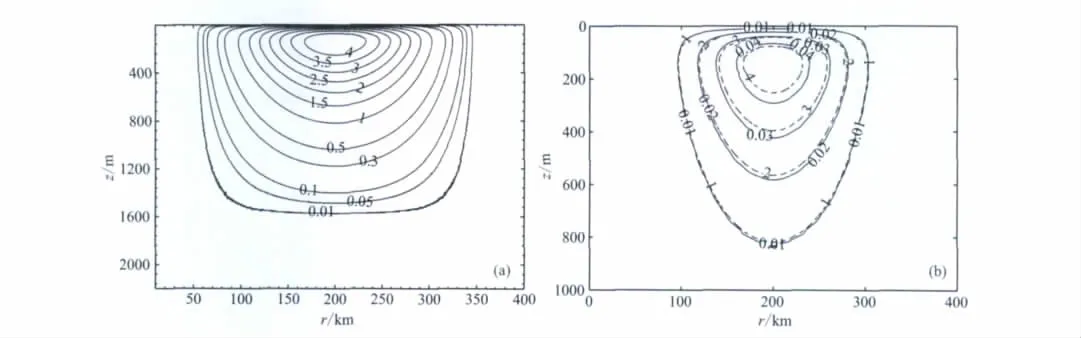
图7 海水中温度差的等值线图（a）最大流速为1.0m·s-1；（b）最大流速为1.0m·s-1（虚线）和0.01m·s-1（实线）对比图.Fig.7 Temperature perturbation contours in water（a）The maximum current 1.0m／s；（b）Comparison of temperature perturbation contours between the maximum current 1.0（dashed lines）and 0.01m／s（solid lines）.

那么由公式（5）和（17）可得，温度差与涡有效半径r0和最大流速U0有关.图8给出了不同r0情况下最大温度差值ΔTmax随U0的变化曲线.可以看出，对于同一r0而言，当U0较小时，ΔTmax和U0近似呈线性关系；随着U0的增大，这种线性关系被破坏，拟合后发现ΔTmax与γ之间存在以下关系：

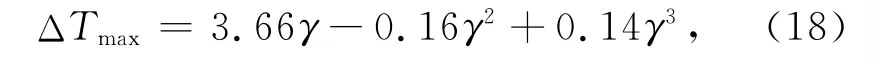
比较（16）式和（18）式，可以推导出目标地层成像的最大地形畸变率满足：

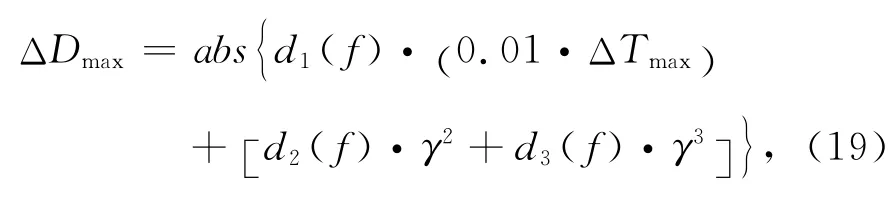
其中d1（f），d2（f），d3（f）是震源频率f 的函数，d1（f）是100量级，d2（f）是10-2量级，d3（f）是10-3量级.当γ≤0.1时，ΔDmax几乎完全由ΔTmax决定，γ的高级项可以忽略不计.

由（19）式和（18）式可得：当有效涡强度较小时，线性项居于主导地位，地震成像的失真率随有效涡强度变化比较缓慢；当有效涡强度较大时，高阶项渐渐居于主导地位，地震成像的失真率随有效涡强度的变化较快.特别地，当ΔTmax小于0.01°时，有ΔDmax＜10-4，旋涡对目标地层成像的影响可以忽略不计，这和地震海洋学的研究结果吻合.结合（18）式可得，当γ＜10-2时，旋涡对地震成像不再有影响.

分析可知，温度差是决定地形畸变率的关键参数.那么这一结论能否用来解释前面2.4节提出的水深与地形畸变率的关系呢？为此将深度无量纲化.图9给出的是涡群中第一个涡在水深2500m和5000m时的温度差等值线图.由图中可以看出，水深5000m时最大温度差比2500m时的大了约0.5°，并且5000m时温度差的梯度也较大.由此证明，涡对地震成像的影响确实随水深增加而增加.

图8 温度差的最大值与U0的关系Fig.8 Maximum temperature perturbation change as a function of U0

6 结 论

本文研究充分表明，中尺度涡对深海地震成像的影响是不可以忽略的，在处理深海地震勘探资料时必须考虑水体的非均匀性，以提高地震成像精度.

与以往的地震数值模拟不同，本文将含有中尺度涡的海水层视为非均匀运动水体，并将PE方法与地震数值模拟方法相结合，讨论了震源频率较低时中尺度涡对目标地层成像的影响.主要结论如下：

（1）中尺度涡群内的速度有很强的非均匀性，这种非均匀性对地震波传播产生干扰，从而使目标地层的成像发生畸变.特别地，涡与涡之间的相互作用会产生复杂反射层，从而加剧了目标地层成像的畸变.

图9 2500m和5000m海深时温度差的等值线图Fig.9 Comparison of temperature perturbation contours between the water depth of 2500mand 5000m

（2）基于文中所给的南海暖涡，得到了有效涡强度、温度差与最大地形畸变率的定量关系（19）式，这个关系式揭示了温度差在地形畸变率中占有重要地位.当有ΔTmax≤0.01°时，旋涡对地震成像不再有影响.

（3）中尺度涡引起的温度差随着海水深度的增加而增大，从而导致地震成像畸变率也越大.

（References）

[1]Holbrook W S，Paramo P，Pearse S，et al.Thermohaline fine structure in an oceanographic front from seismic reflection profiling.Science，2003，301（8）：821-824.

[2]Biescas B，Sallarès V，Pelegr J L，et al.Imaging meddy finestructure using multichannel seismic reflection data.Geophysical Research Letters，2008，35（11）：L11609，doi：10.1029／2008GL033971.

[3]Ruddick B.Sounding out ocean fine structure.Science，2003，301（5634）：772-773.

[4]宋海斌，Luis P，王东晓等.海洋中尺度涡与内波的地震图像.地球物理学报，2009，52（11）：2775-2780.Song H B，Luis P，Wang D X，et al.Seismic images of ocean meso-scale eddies and internal waves.Chinese J.Geophys.（in Chinese），2009，52（11）：2775-2780.

[5]Wood W T，Holbrook W S，Sen M K，et al.Full waveform inversion of reflection seismic data for ocean temperature profiles.Geophysical Research Letters，2008，35（4）：L04608，doi：10.1029／2007GL032359.

[6]Pinheiro L M，Song H，Ruddick B，et al.Detailed 2-D imaging of the Mediterranean outflow and meddies off W Iberia from multichannel seismic data.Journal of Marine Systems，2010，79（1-2）：89-100.

[7]胡毅，刘怀山，陈坚等.地震海洋学研究进展.地球科学进展，2009，24（10）：1094-1104.Hu Y，Liu H S，Chen J，et al.Recent progress in seismic oceanography.Advance in Earth Science （in Chinese），2009，24（10）：1094-1104.

[8]宋海斌，董崇志，陈林等.用反射地震方法研究物理海洋—地震海洋学简介.地球物理学进展，2008，23（4）：1156-1164.Song H B，Dong C Z，Chen L，et al.Reflection seismic methods for studying physical oceanography：Introduction of seismic oceanography.Progress in Geophys （in Chinese），2008，23（4）：1156-1164.

[9]Kulkarni R S，Siegmann W L，Collins M D，et al.Nonlinear pulse propagation in shallow-water environments with attenuating and dispersive sediments.Journal Acoust.Soc.Am.，1998，104（3）：1356-1362.

[10]Parker C E.Gulf stream rings in the Sargasso Sea.Deep-Sea Res，1971，18：981-993.

[11]Henrick R F，Siegmann W L，Jacobson M J.General analysis of ocean eddy effects for sound transmission applications.Journal Acoust.Soc.Am.，1977，62（4）：860-870.

[12]Baer R N.Calculations of sound propagation through an eddy.Journa Acoust.Soc.Am.，1980，67（4）：1180-1185.

[13]Nysen P A，Power P S.Sound propagation through an East Australian Current eddy.Journal Acoust.Soc.Am.，1978，63（5）：1381-1388.

[14]Jian Y J，Zhang J，Liu Q S，et al.Effect of mesoscale eddies on underwater sound propagation.Applied Acoustics，2009，70（3）：432-440.

[15]Krahmann G，Brandt P，Klaeschen D，et al.Mid-depth internal wave energy off the Iberian Peninsula estimated from seismic reflection data.J.Geophys.Res，2008，113（C12）：C12016，doi：10.1029／2007JC00467.

[16]Nakamura Y，Noguchi T，Tsuji T，et al.Simultaneous seismic reflection and physical oceanographic observations of oceanic fine structure in the Kuroshio extension front.Geophys.Res.Lett.，2006，33（23）：L23605，doi：10.1029／2006GL027437.

[17]Kormann J，Cobo P，Prieto A.Perfectly matched layers for modelling seismic oceanography experiments.Journal of Sound and Vibration，2008，317（1-2）：354-365.

[18]Robertson J S，Siegmann W L，Jacobson M J.Current and current shear effects in the parabolic approximation for underwater sound channels.J.Acoust.Soc.Am.，1985，77（5）：1768-1780.

[19]Godin O A.Parabolic approximation in the theory of the sound propagation in Three-Dimensionally heterogeneous media.Doklady Physics，2000，45（8）：367-371.

[20]Jerzak W，Collins M D，Evans R B，et al.Parabolic equation techniques for seismic waves.Pure and Applied Geophysics，2002，159（7-8）：1681-1689.

[21]Collis J M，Siegmann W L，Jensen F B，et al.Parabolic equation solution of seismo-acoustics problems involving variations in bathymetry and sediment thickness.J.Acoust.Soc.Am.，2008，123（1）：51-55.

[22]吴培木，郭小钢，吴日升.台湾省恒春西南海域声速场分析.台湾海峡，2001，20（3）：279-286.Wu P M，Guo X G，Wu R S.Analyses of sound velocity field in southwest sea area off Hengchun of Taiwan.J.Oceanogr.Taiwan Strait.（in Chinese），2001，20（3）：279-286.

[23]Eckart C.Properties of Water.2.The equation of state of water and sea water at low temperatures and pressures.Am.J.Sci，1958，256：225-240.

[24]Ergin K.Energy ratio of the seismic waves reflected and refracted at a rock-water boundary.Bull.Seism.Soc.Am.，1952，42（4）：349-372.

[25]Hunt J M，Hays E E，Degens E T，et al.Red sea：detailed survey of hot-brine areas.Science，1967，56（3774）：514-516.