一种改进的逆变器并联功率解耦控制策略

，，

（教育部光伏系统工程研究中心 合肥工业大学能源研究所，安徽 合肥230009）

1 引言

由多台逆变器组成并联系统可实现大容量和冗余供电，各逆变器根据自身容量来均分负载功率需求。逆变器无互联线并联控制方式中，下垂控制根据各逆变模块自身的变量来实现并联均流，无需通信线路，系统抗干扰能力强、扩容方便、可靠性高[1]，得到了广泛的应用。

传统下垂控制理论认为线路阻抗主要为感性，从而忽略电阻，推导出逆变器输出电压的频率与有功功率、电压幅值与无功功率之间近似解耦的关系。但实际中应用的多是低压并联系统，其线路阻抗的阻性分量为主要部分，逆变器输出的频率将和有功及无功功率都有关，输出电压也与有功和无功功率有关，即产生了功率耦合问题。文献[2]引入负载和线路阻抗参数来对有功和无功进行变换，变换后的有功无功满足传统下垂控制特性方程，实现解耦。文献[3]提出“类功率”下垂控制算法，解耦思想与文献[2]类似。还有一种思路就是通过控制策略使逆变器输出基频等效阻抗为感性的虚拟阻抗法[1]，从而使传统下垂特性的假设成立。文献[4]将有功无功功率进行正交旋转变换，变换矩阵只与线路阻抗角的余角有关，实现解耦。以上大多属于从功率侧进行变换的解耦方法，会带来有功功率不能均分的问题[2]。

本文基于功率解耦控制的思想，提出了改进的下垂特性控制策略，将逆变器输出电压的频率和幅值进行正交旋转变换，实现功率解耦控制，并在变换后的下垂特性中加入了微分环节，以提高系统的动态特性。对变换的思路及变换后涉及到的工作范围问题进行了讨论，并以2台单相全桥电压型逆变器搭建了并联系统模型，在Simulink下进行稳态和动态性能的仿真，仿真结果证实了该策略的有效性和可行性。

2 功率解耦控制策略

2.1 传统的频率和电压下垂理论

2台逆变器并联的等效电路如图1所示。

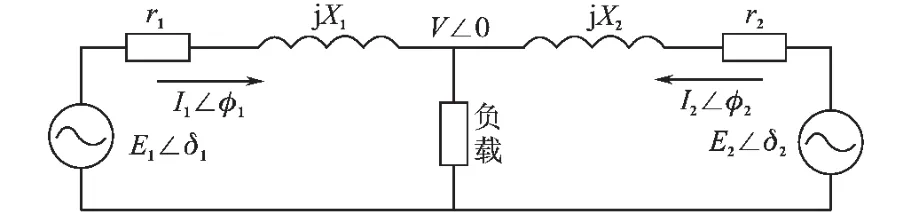
图1 逆变器并联等效电路Fig.1 Equivalent circuit of parallel inverters

先计算单个逆变器输出功率，逆变器输出的复功率为

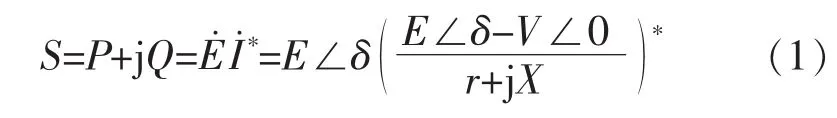
所以

在常规高压电力系统中，有线路阻抗X≫r，所以忽略上式中的r，由于线路阻抗通常远小于负载阻抗，即E和V的相位差会很小，认为δ很小，所以近似有 sin δ=δ，cos δ=1，则式（2）和式（3）可以化简为

可见有功功率主要取决于相位差δ，无功功率主要取决于逆变器输出电压幅值E。即各并联逆变器单元输出的有功和无功分别与其输出电压的相位差和幅值有近似的解耦关系。相比于相位，频率更容易检测和控制，控制频率可以动态地调整相位。所以，控制逆变器输出电压的频率和幅值就能分别调整输出的有功功率和无功功率。相应的下垂特性为

式中：ω0，E0分别为逆变器空载输出电压的角频率和幅值；k1和k2分别为有功和无功下垂系数。

并联运行时，输出有功功率大的逆变器通过下垂特性减小频率给定，从而减小有功功率输出，输出有功功率小的逆变器通过下垂特性增加频率给定，从而增加有功功率输出，最终达到有功功率均分。无功功率调整同理。

注意到式（4）和式（5）是基于线路阻抗主要为感性的假设。在低压并联系统中，线路阻抗中电阻为主要成分，电阻不能被忽略，这种情况下，调节电压幅值将会影响有功功率，调整频率将会影响无功功率。因此，传统的下垂方法将会导致有功和无功功率控制的耦合，并可能引起正反馈，产生稳定性问题[2]。

2.2 基于功率变换的解耦控制

考虑到ω和E都既和P有关也和Q有关，那么可以将P和Q进行线性组合，使组合后的值分别只对应于ω和E。线性组合的系数可能与负载和线路阻抗的参数有关[2-3]。引入变换矩阵T1[4]，

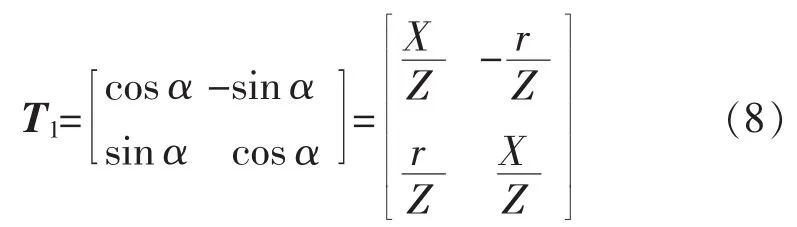
式中：α为线路阻抗角的余角；Z=r+jX。

对P和Q进行变换，则

上述变换的几何意义就是将原向量旋转α角，即T1为正交旋转变换，正交变换的特性是旋转后向量的长度不变。 根据式（2）、式（3）可得：

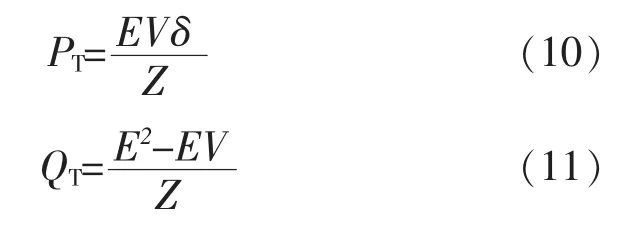
可见通过变换，实现了功率的解耦，即变换后的有功功率主要取决于相位差δ，变换后的无功功率主要取决于逆变器输出电压幅值E。为了能直观地说明变换的原理以及变换后各物理量的关系，利用正交变换的性质，可以得到图2。

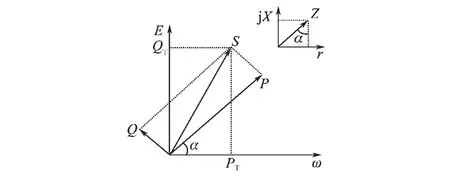
图2 有功无功旋转变换后与电压频率幅值的关系图Fig.2 Relationship diagram with frequency and voltage after transformation of power

这种从功率侧进行变换实现解耦的方法会产生实际有功功率不能均分的问题，对于并联的2台逆变器有

稳态时有P1T=P2T，逆变器双环控制中外环常采用瞬时电压进行PI调节，而瞬时电压是交流量，稳态时输出电压是有差的，则下垂控制后Q1T≠Q2T，同时T1的行列式值为1，是非奇异的，那么可以得到 P1≠P2，Q1≠Q2，即功率变换会使得实际有功无功都不能均分。此外，变换后的功率是实际功率的线性组合，不宜加入微分补偿环节调节动态特性。

2.3 改进的下垂特性控制策略

为了解决功率旋转变换后带来的问题，同时又能达到与其等效解耦的效果，那么可以在图2中对ω和E进行反向旋转变换，变换后的各物理量的关系如图3所示。

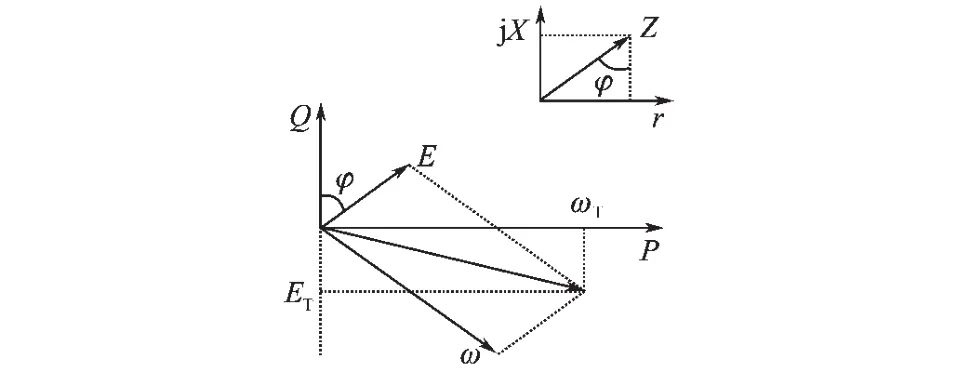
图3 电压幅值频率旋转变换后与有功无功的关系图Fig.3 The relationship diagram with active and reactive power after transformation of frequency and voltage

相应的变换式为[5]

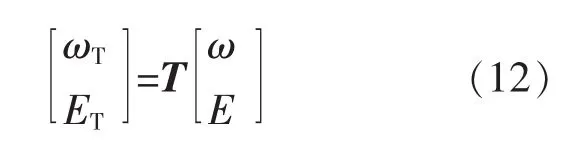
变换矩阵

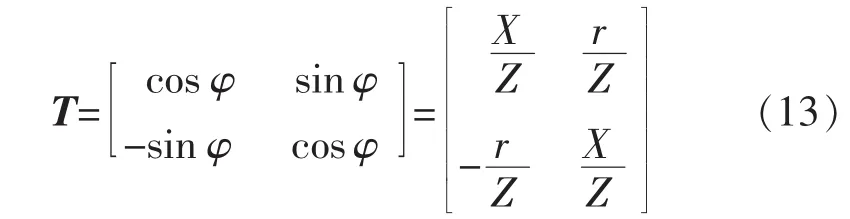
对比图2和图3可知，两种变换下，各物理量之间的相对位置没有变化，所以电压频率幅值变换后可以达到与有功无功旋转变换后同样的解耦效果，即输出功率可以被直接、精确的控制，并完全解耦。

逆变器在并联运行过程中会经常出现负载突变、逆变器加入退出的情况，输出电压的谐波成分、线路阻抗参数的不一致、逆变器开关器件的开关特性及死区时间的不一致都会产生并联系统动态环流，此外，并联系统常采用时间常数较大的一阶惯性环节来滤除功率纹波，这就限制了系统的响应速度。为了补偿功率计算的滞后及抑制动态环流的需要，在解耦后的下垂特性中加入有功和无功功率微分补偿环节来提高系统的动态性能[7]。则改进的下垂特性变为

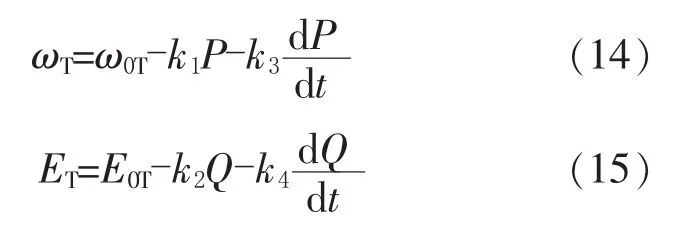
实际并联系统运行时，其ω和E有规定的运行范围，这就要求按照式（14）、式（15）计算出的ωT和ET进行反变换后仍在ω和E规定的范围内。设T-1为T的逆矩阵，相应的反变换为

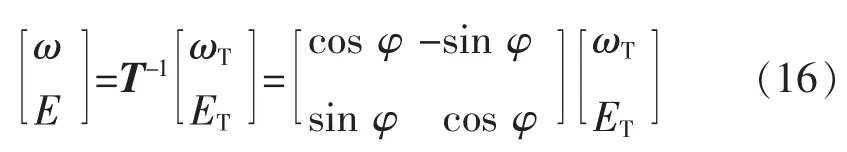
此外，为了使并联系统工作时负载功率能有效均分，就要求按改进的下垂特性算法算出的ωT和ET能够经过相同的反变换得到实际的ω和E，即要求各逆变器的φ是相同的。实际中，若各逆变器的φ不确定或不相同，同时又确保改进的下垂特性可以有效使用，作为一种折中考虑，可统一选为45°，即对应于R/X=1/1。通过仿真分析可知，在线路阻抗角为其他值时，系统也有很好的稳态精度和稳定性，即改进的下垂特性对参数变化具有较强的适应性。

3 并联系统控制结构

图4 逆变器并联系统结构框图Fig.4 Block diagram of parallel inverters system

根据本文提出的改进下垂控制方法，建立了由2台单相逆变器组成的并联系统[8]，逆变器并联系统的结构框图如图4所示。逆变器主电路为电压型全桥结构，输出采用LC滤波器，控制方式采用的是电压外环电感电流内环的双环SPWM控制。电压外环采用PI调节器，主要目的是稳定负载电压，提高稳态精度，同时保证输出电压波形质量。电流环采用P调节器，主要目的是提高系统的动态响应。同时，由于电感电流是电流调节器输出与电感作用的积分结果，因而采用电感电流反馈不仅具有很好的跟踪性能，而且还有内在的限流保护功能[1]。控制器工作时，首先检测逆变器的输出电压和电流，并计算输出的有功和无功功率，然后根据式（14）、式（15）改进的下垂特性计算出ωT和ET，再根据式（16）变换到实际的频率和电压幅值，合成参考电压后，作为双环控制的电压给定，从而控制输出的功率。

4 控制策略的仿真分析

为了验证新算法的可行性，在Matlab/Simulink下搭建了2台逆变器并联的仿真模型，仿真参数如下：线路阻抗为0.05+j0.031 4 Ω，输出电压有效值220 V，频率50 Hz，逆变器直流输入 540 V，输出滤波电感 1 mH，电容 10 μF，负载电阻48.4 Ω，负载电感154 mH，下垂及微分系数k1=1×10-4，k2=5×10-4，k3=1.6×10-6，k4=2.4×10-6。 考虑到实际系统中逆变器锁相环锁相精度有限，必然存在微小偏差，仿真条件中设置并联初始相位偏差为2。仿真波形如图5所示。

图5为逆变器1带载工作，0.1 s时逆变器2

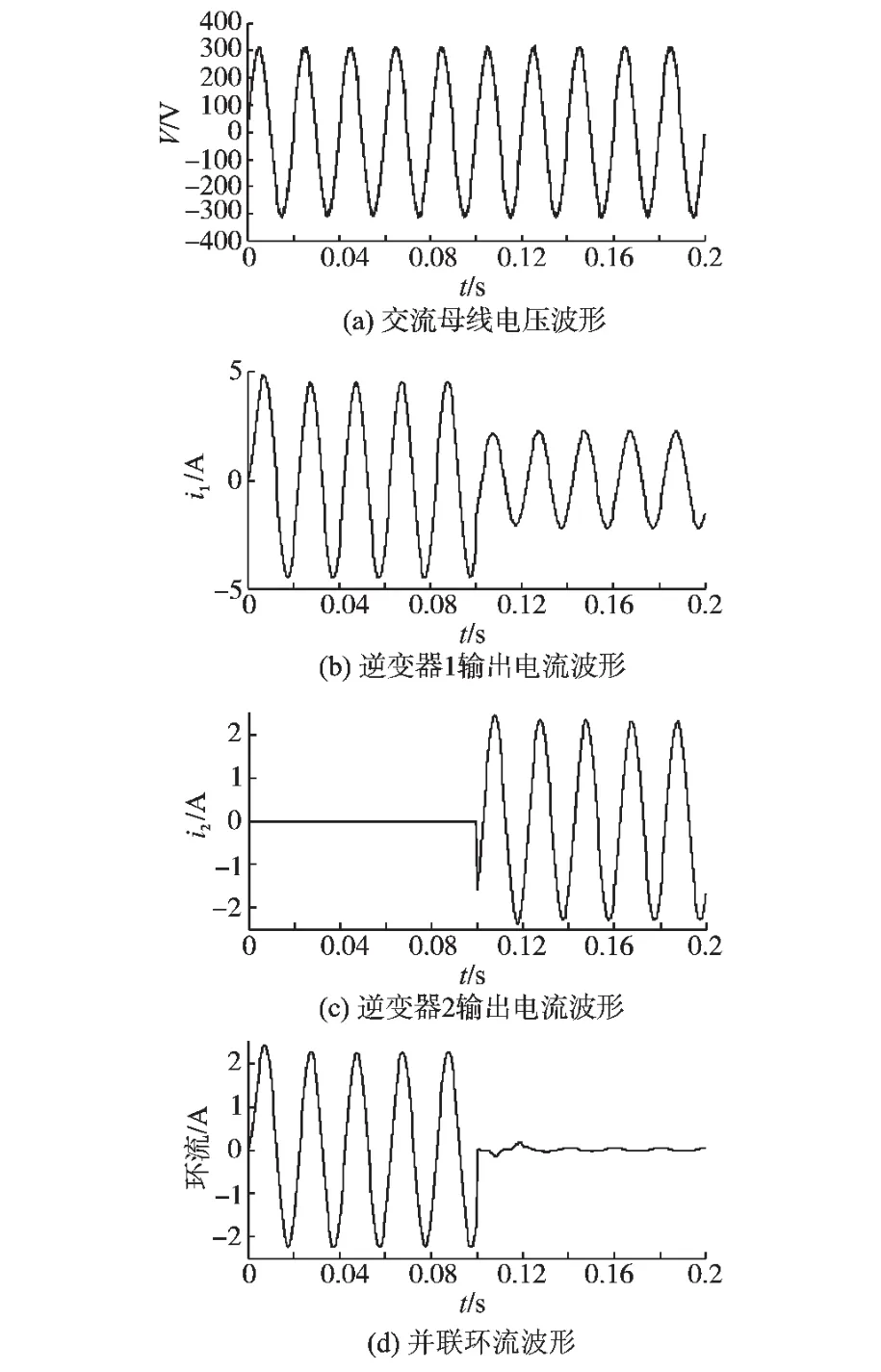
图5 逆变器2在0.1 s并入前后的仿真波形Fig.5 Simulation waveforms before and after the parallel of inverter 2 at 0.1 s

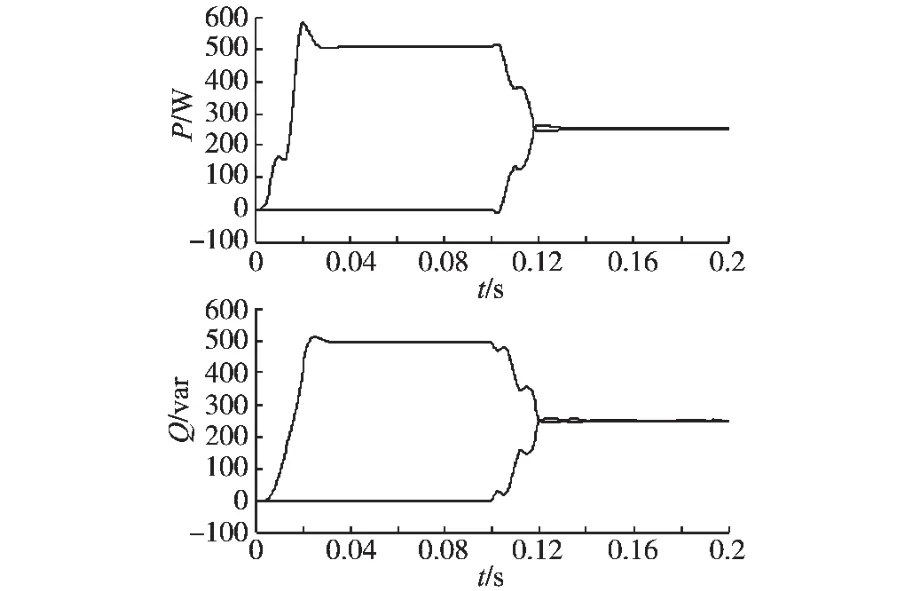
图6 逆变器2在0.1 s时并入后的输出功率波形Fig.6 Simulation waveforms of output power after the parallel of inverter 2 at 0.1 s

图7为并联系统满载工作时，0.1 s负载突变到半载时的逆变器输出电流波形，可见，在系统负载突变时，逆变器输出电流都有良好的动态和稳态性能。

5 结论

本文分析了逆变器并联系统中传统下垂特性和从下垂特性功率侧实现解耦的控制方法的不足，提出了一种基于电压频率幅值旋转变换并加入微分环节的改进的下垂特性控制方法，结合2台并联的单相逆变器建立了仿真模型，理论分析和仿真结果表明，改进的下垂控制方法在线路阻抗的阻感性成分均不可忽略时，仍能够对并联系统的有功和无功功率很好的均分，稳态环流较小，系统具有良好的动态和稳态性能并且对参数变化具有较强的适应性。

［1］鞠洪新.分布式微网电力系统中多逆变电源的并网控制研究［D］.合肥：合肥工业大学，2006.

［2］林新春，段善旭，康勇，等.UPS无互联线并联中基于解耦控制的下垂特性控制方案［J］.中国电机工程学报，2003，23（12）：117-122.

［3］阚志忠，张纯江，薛海芬，等.微网中三相逆变器无互联线并联新型下垂控制策略［J］.中国电机工程学报，2011，31（33）：68-74.

［4］Brabandere K D，Bolsens B，Keybus J V，et al.A Voltage and Frequency Droop Control Method for Parallel Inverters［J］.IEEE，2007，22（4）： 1107-1115.

［5］Li Yan，Li Yun Wei.Virtual Frequency-voltage Frame Control of Inverter Based Low Voltage Microgrid ［C］∥IEEE，2009：1-6.

［6］Li Yan，Li Yun Wei.Decoupled Power Control for an Inverter Based Low Voltage Microgrid in Autonomous Operation ［J］.IEEE，2009，1（4）：1797-1803.

［7］Guerrero J M，Vicun˜a L G，Matas J，et al.A Wireless Controller to Enhance Dynamic Performance of Parallel Inverters in Distributed Generation Systems ［J］.IEEE， 2004， 19（5）：1205-1213.

［8］田里思，周永鹏.UPS无互联线并联控制技术的Saber仿真［J］.电气传动，2011，41（9）：26-29.