一种改进的InSAR干涉图复数空间自适应滤波

易辉伟 ，朱建军 ，陈建群 ，齐艳妮，李佳

(1. 中南大学 地球科学与信息物理学院，湖南 长沙，410083；2. 湖南省普通高校精密工程测量及形变灾害监测重点实验室，湖南 长沙，410083)

合成孔径干涉雷达(InSAR)能够全天候、全天时、无接触式地获取地球表面形变的精密信息，已广泛用于地震、滑坡、冰移、火山及矿山沉降等现象监测中。然而，受热噪声、时间去相关、空间去相关等因素影响[1]，INSAR干涉图像不可避免地存在大量噪声，难以解缠以至于无法得到数字地面高程模型及形变结果。因此，如何更好地对干涉图进行去噪，成为INSAR实际应用中亟待解决的问题[2]。干涉图滤波方法分为频率域和空间域2类，频率域滤波是将图像的滑动小窗口(通常为 32像素×32像素)内像素通过傅里叶变换为功率谱，并对该功率谱进行平滑再通过反傅里叶变换到图像空间。频率域滤波方法的代表为Goldstein[3]滤波。Baran等[4]应用相干值改善Goldstein的滤波因子，使其更具有自适应性。Li等[5]引入干涉图的视数及相位标准偏差来调整滤波因子，使干涉图相位信息保持和算法稳健性得到有效改善；孙倩等[6]应用信噪比控制滤波强度，对低信噪比区域强滤波，高信噪比区域弱滤波。于晓歆等[7]应用最大最小值法对相位标准偏差进行归一化处理后采用其指数作为滤波因子，得到较好滤波效果。Goldstein方法去噪能力较强，但会损失大量边缘细节信息，给 DEM和形变测量带来误差。近年发展的矢量分离式小波滤波[8]和小波-维纳组合滤波[9]能在一定程度上保留细节，其小波基的构造及小波软硬阈值的选取还需要良好的智能决策。卡尔曼滤波[10]和基于格网值法[11]都是通过估计相位来滤波图像，不同的估计方法将得到不同的滤波结果。空间域是逐像素进行的，通过周围像素来影响中心像素值达到去噪目的，将模板(通常为3×3像素)与中心像素周围对应位置进行卷积，得到新的中心像素。均值滤波和中值滤波简单易行但未考虑干涉图噪声强弱的变化及图像的条纹特征，易引起条纹混迭。作为空间域滤波方法代表的Lee滤波[12]通过局部解缠估计中心像素邻域内的坡度，从而根据乘性噪声模型改善中心像素。由于带噪声的局部解缠计算复杂、费时且不准确，Lee提出了修正Lee滤波，即将包含边缘的局部区域分为8个方向，利用局域梯度边缘检测方法确定边缘的方向，并判定中心像素所在方向，并用该方向的像素取值改变中心像素，此方法能更好地保护条纹边缘；尹宏杰等[13]根据同质区域方差最小的原理确定中心像素所在方向，并根据干涉图的相干性来选择融合方向窗口的数量，增强Lee算法的稳健性，但算法极为复杂。数学形态法[14]在Lee滤波的非同质区采用膨胀腐蚀法找到边缘，能有效增强边缘。王兴旺等[15]提出边缘保持法，其原理也是找到中心像素所在方向，该方法受窗口大小和噪声强弱影响较大。文献[16-17]应用区域增长法并以相位变化最小为准则自适应选择滤波窗口，取得较好滤波效果，但未能考虑条纹率。李佳等[18]结合频率域和空间域滤波的优点设计二级滤波，并取得一定成效。近年来发展的堆栈法[19]将图像分成若干个二进制文件再通过布尔判断式分别滤波。乘性加性模型法[20]将对角线相位噪声划为乘性，非对角线噪声划为加性，该方法有待进一步验证。廖明生等[21]提出的复数空间自适应滤波是根据梯度确定中心像素纵横方向邻域内各像素的权系数，卷积后得到中心像素的新值，其算法简单，效果明显，迭代3～5次即可。本文作者首先介绍复数空间自适应滤波算法，通过增加 45°和 135°梯度计算进行斜方向条纹的探索，并根据相干系数确定条纹边缘的尺度函数 k，进而改善权系数的表达式；然后，以模拟数据和真实数据作为实验数据，分别与复数空间自适应、Lee滤波、基于信噪比的Goldstein及最优化方向融合方法进行比较，结果表明本文方法在去噪和边缘信息保持方面较前4种方法都有明显改善，局部自适应性更强。

1 复数空间自适应滤波方法

InSAR干涉图由复数构成，图像显示的数据为[-π，+π]之间的缠绕相位存在跳跃性，因此不能对其直接平滑，而应将复数的实部和虚部分别滤波，再进行复数重构，复数空间自适应滤波方法的算法可用下式表示。

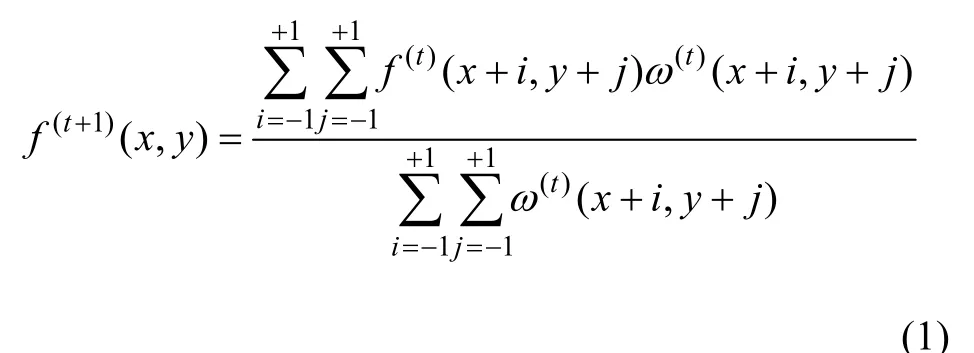
其中： f(t)(x + i , y + i )为 (x + i, y + j )处像素的第t次迭代， ω(t)(x+ i , y +j)为(x + i,y + j )处像素的权系数。其思想是：(x，y)处像素值的滤波值是以其周围 3×3像素为窗口，对窗口内每个像素进行加权平均而得。权系数可定义为：

其中：s′(t)(x)为信号 s(t)(x)的一阶导数，在此为梯度计算，见式(3)和(4)；k为尺度函数，确定在平滑过程中可保留的边缘幅度，通常取梯度最大值的1/3～1/2。如果某点的信号梯度大于k，则认为该点处于边缘上，边缘点在滤波窗口对应的权系数减小，即尽量不参与平滑，使边缘得以保留；反之，若信号梯度小于 k，则对应非边缘的点，其权系数就会变大，在非边缘区域梯度低于 k，窗口内各权系数接近，在较大程度上参与平滑，从而达到去除噪声的效果。

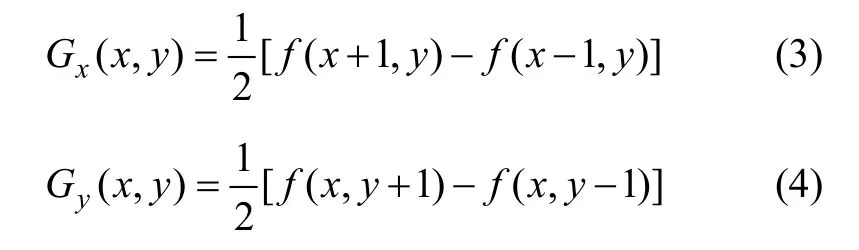
其中：Gx(x，y)为(x，y)像素的水平方向梯度；Gy(x，y)为(x，y)像素的垂直方向梯度。

2 改进的复数空间自适应滤波

复数空间自适应算法存在不足，如梯度计算只考虑水平和垂直方向，不够全面；尺度函数k的取值为1/3～1/2的最大梯度这一经验值。事实上，噪声强弱会直接影响到梯度的变化，条纹尺度函数的固定取值不能适应噪声的强弱变化，会降低对条纹判断的准确性，其局部适应性不强；此外，人工选取k费时且主观性强。针对以上不足，作如下改进：

(1) 梯度计算中加入斜方向梯度。3×3像素的滤波窗口如图1所示。从图1可见：像素5周围有8个像素，梯度方向不仅包括4，5和6水平方向以及2，5和8垂直方向，还应包括3，5和7所形成的45°以及1，5和9 所形成的135°这2个斜方向，其梯度计算见式(5)和(6)。因而，滤波窗口权系数相应地改为式(7)；

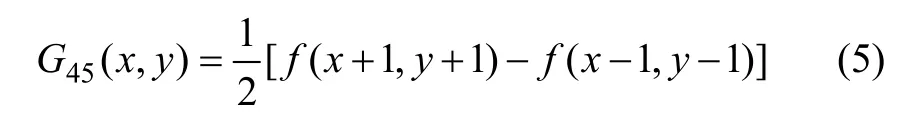
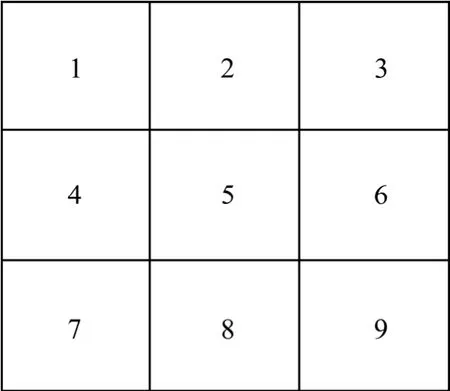
图1 3像素×3像素的滤波窗口Fig.1 3×3 pixels filter window

其中：G45(x，y)为 45°方向梯度；G135(x，y)为 135°方向梯度。

(2) 用相干系数改善尺度函数k。如前所述，k取值大则平滑程度大，即强去噪；取值小则平滑程度小，即弱去噪。而INSAR干涉图中噪声分布并不均匀，有的区域噪声强，有的区域噪声弱，对其滤波较理想的结果是强噪区得到强滤波，弱噪区得到弱滤波并能保持条纹形状，显然k取固定值不能满足这一要求。噪声的强度由噪声相位标准偏差决定，噪声相位标准偏差大，则噪声强；噪声相位标准偏差小，则噪声弱，噪声相位标准偏差与相干系数和视数存在以下关系[22]：

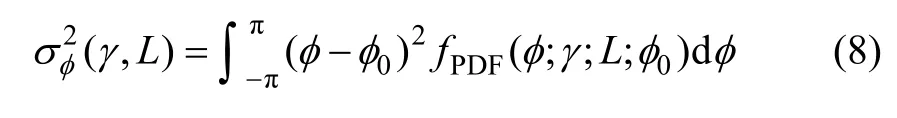
其中： σφ2为相位方差；γ为干涉图相干系数；L为视数；φ为干涉图相位；φ0为相位的期望；fPDF为相位概率密度函数。

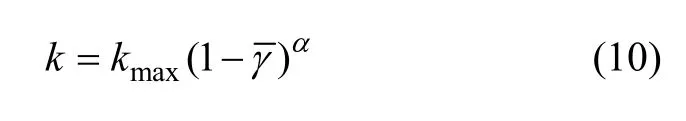
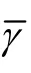
图2 噪声相位标准偏差与相干系数及视数关系Fig.2 Relationship between phase standard deviation and coherence&look number

α与视数L有关，通过大量数据模拟试验得到：

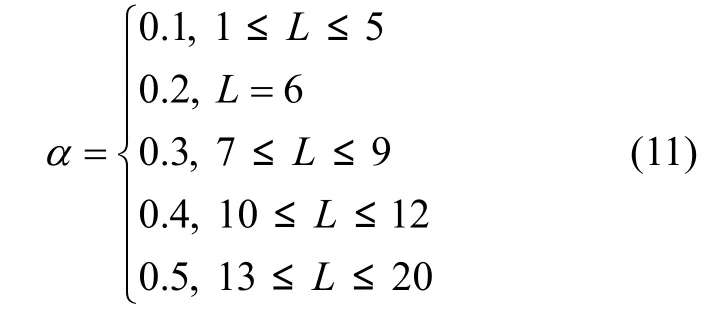
3 实验结果及分析

3.1 模拟干涉图实验结果

利用多分形技术模拟数字高程模型，再根据ERS1/2的成像几何参数和200 m垂直基线模拟出缠绕的相位，最后根据式(9)模拟出给定视数的相位噪声。图3(a)所示为512像素×512像素的模拟无噪相位图，图3(b)所示为加噪相位图，图3(c)～(g)所示为分别用复数空间自适应滤波(取尺度函数为1/3kmax)、Lee滤波、基于信噪比的Goldstein、最优方向融合滤波以及本文方法对其进行滤波的结果图。从图3可见：5种方法滤波效果都不错，基本复原无噪相位图。本文方法结果(图3(g))与图3(c)相比有明显改善，噪声大量减少，条纹更清晰。整体效果与图 3(d)及图 3(f)中的结果相似，但条纹边缘细微处信息保持得更好，与图 3(a)更为接近，且运行时间要比Lee滤波及最优方向融合滤波快很多。比较图 3(e)与图 3(a)可见：基于信噪比的Goldstein滤波去噪能力较强，特别是同质区内的显著斑点噪声，但同时将一些细节真实信息也当成噪声被滤掉；此外，由于该算法本身的原因还需处理图边像素。无论从噪声的消除程度还是边缘信息的保护程度都可看出本文方法具有明显的优势。图4所示为与图3中对应的第280行剖面图。从该剖面图也可见：本文方法的剖面线光滑程度更高，噪声的抑制效果非常明显，更好地恢复原始无噪相位，与无噪相位图的剖面图4(a)更为吻合。

3.2 真实干涉图实验结果

本文分别选取香港地区和意大利 Etna火山局部区域的干涉图作为实验数据，香港地区数据为 1幅1996-03-18—19 ERS—1/2卫星香港地区的InSAR干涉图，其垂直基线长为100 m。该图条纹密度适中，在此取700像素×1 000像素矩形区域作为实验区域，其滤波结果如图5所示。由于真实图噪声的复杂性，上述几种滤波方法的效果与模拟图相比稍弱，但都明显地去除噪声，增强条纹。为便于观察，选定横向800～925像素、纵向340～425像素区域局部放大，如图6所示。图6(a)所示为分布大量噪声的原始干涉图，图6(b)～(f)所示分别为仍是复数空间自适应滤波、Lee滤波、基于信噪比的Goldstein、最优方向融合滤波以及本文方法的滤波结果。从图6可见：本文方法和复数空间自适应滤波基本去除噪声，而其他3种方法还留有残余噪声。而图 6(f)与图 6(b)相比，既保持条纹的曲度又适当平滑条纹边缘，效果更好。运行速度方面，Lee滤波所需时间8 min，最优方向融合需要4 min，其他方法只需2 min左右。从第240行的相位剖面图7(a)～(f)可进一步看出：图 7(c)～(e)中还有明显较多的噪声，黑框中的图7(b)还残存毛刺；图7(c)～(e)中的相位受噪声影响存在明显的迂回停滞，本文方法的剖面图 7(f)几乎没有毛刺，噪声也大量减少，整条曲线比较平滑，不仅去噪效果良好，而且有效保持相位细节。

意大利Etna火山100×200像素区域的密集条纹干涉图及滤波结果如图8所示。空间自适应滤波的条纹稍显粗糙，而Lee滤波部分条纹明显断开，条纹“僵直”；最优方向融合法条纹很不明显，且光滑度不好；基于信噪比的 Goldstein方法的条纹光滑度及曲度保持也不如本文方法明显。

图3 模拟干涉图滤波结果Fig.3 Simulated interferograms and results of different filters

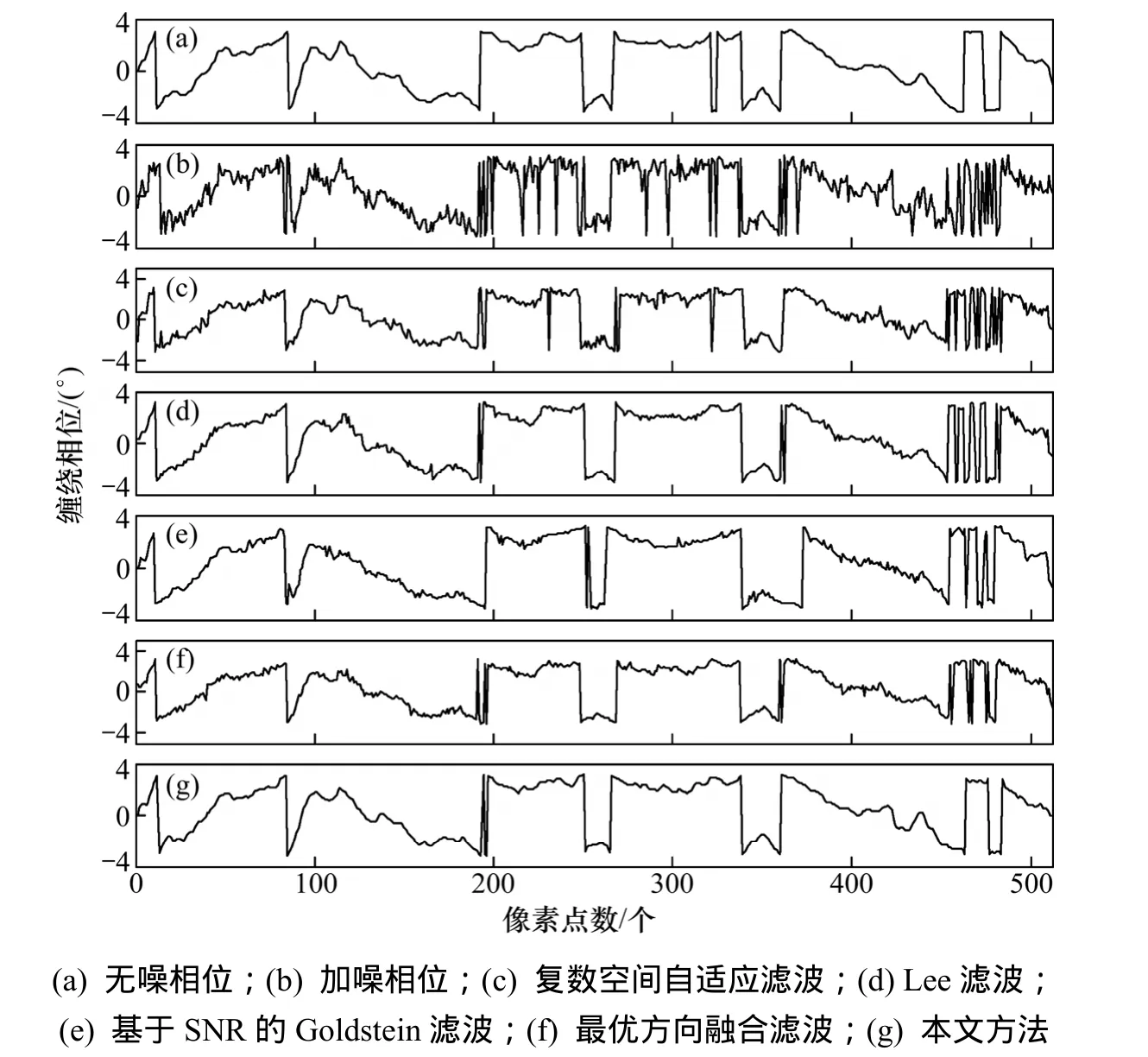
图4 模拟干涉图滤波结果第280行剖面图Fig.4 Profiles of line 280 of filtering results of simulated interferogram

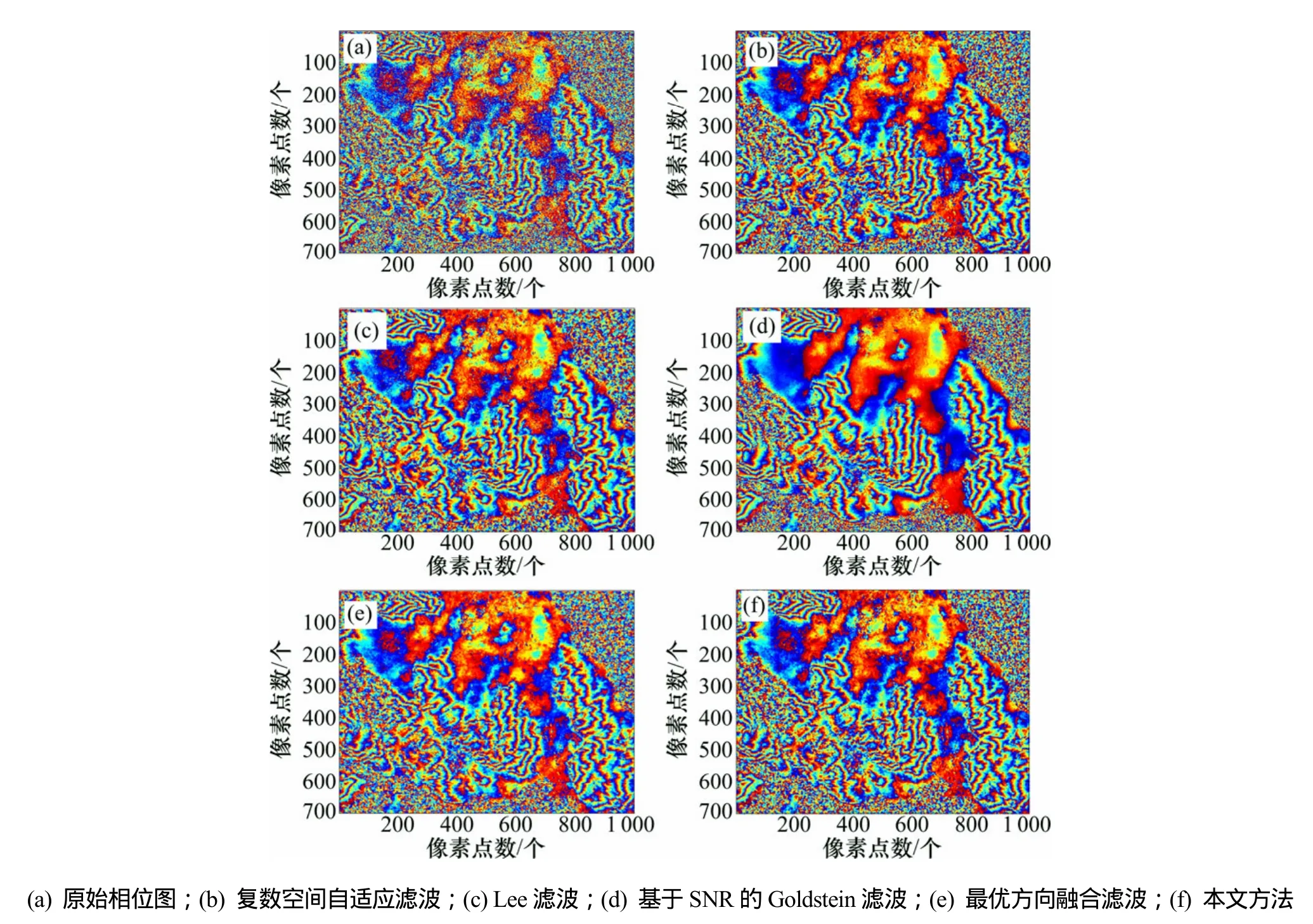
图5 香港地区干涉图滤波结果Fig.5 Filtering results of interferogram in Hong Kong region

图6 香港滤波结果局部放大图Fig.6 Enlarged views of interferogram in local Hong Kong region

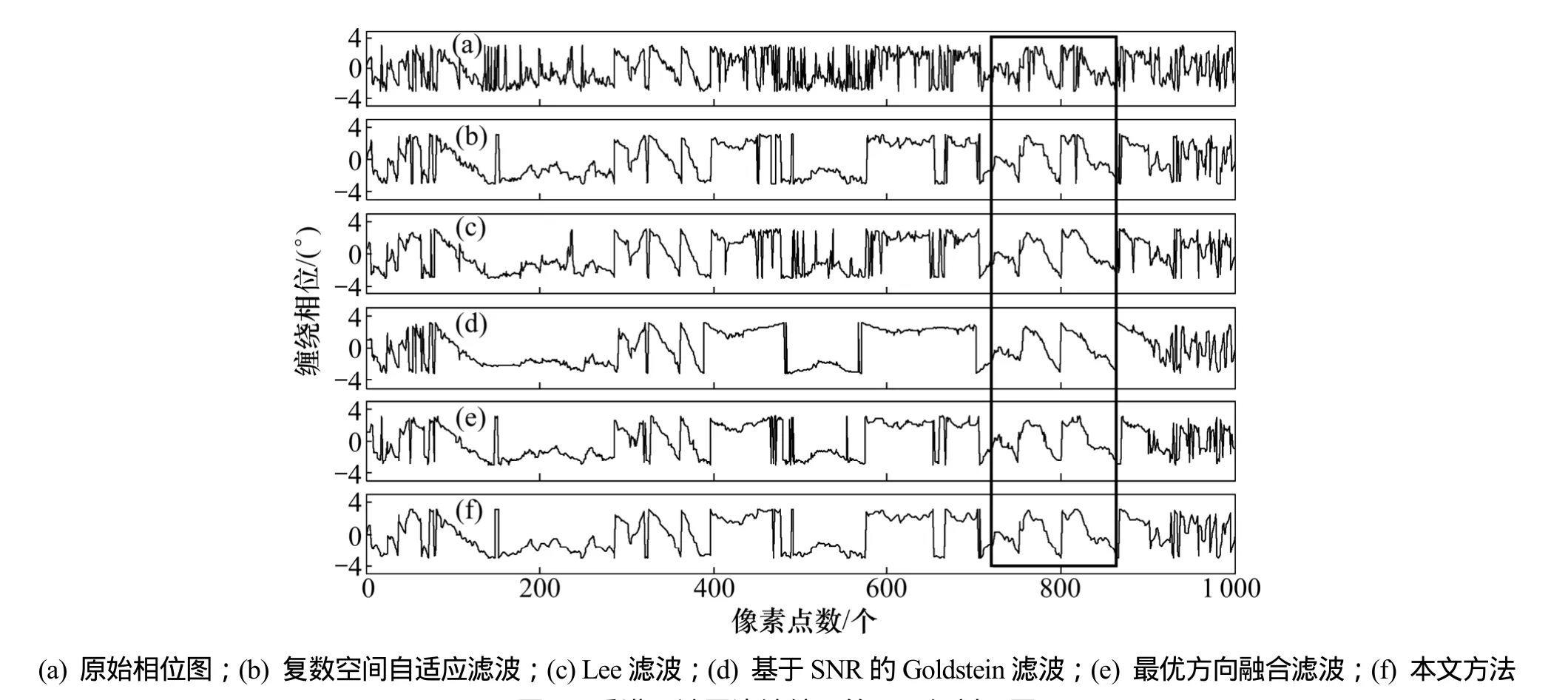
图7 香港干涉图滤波结果第240行剖面图Fig.7 Profiles of line 240 of filtering results in Hong Kong region

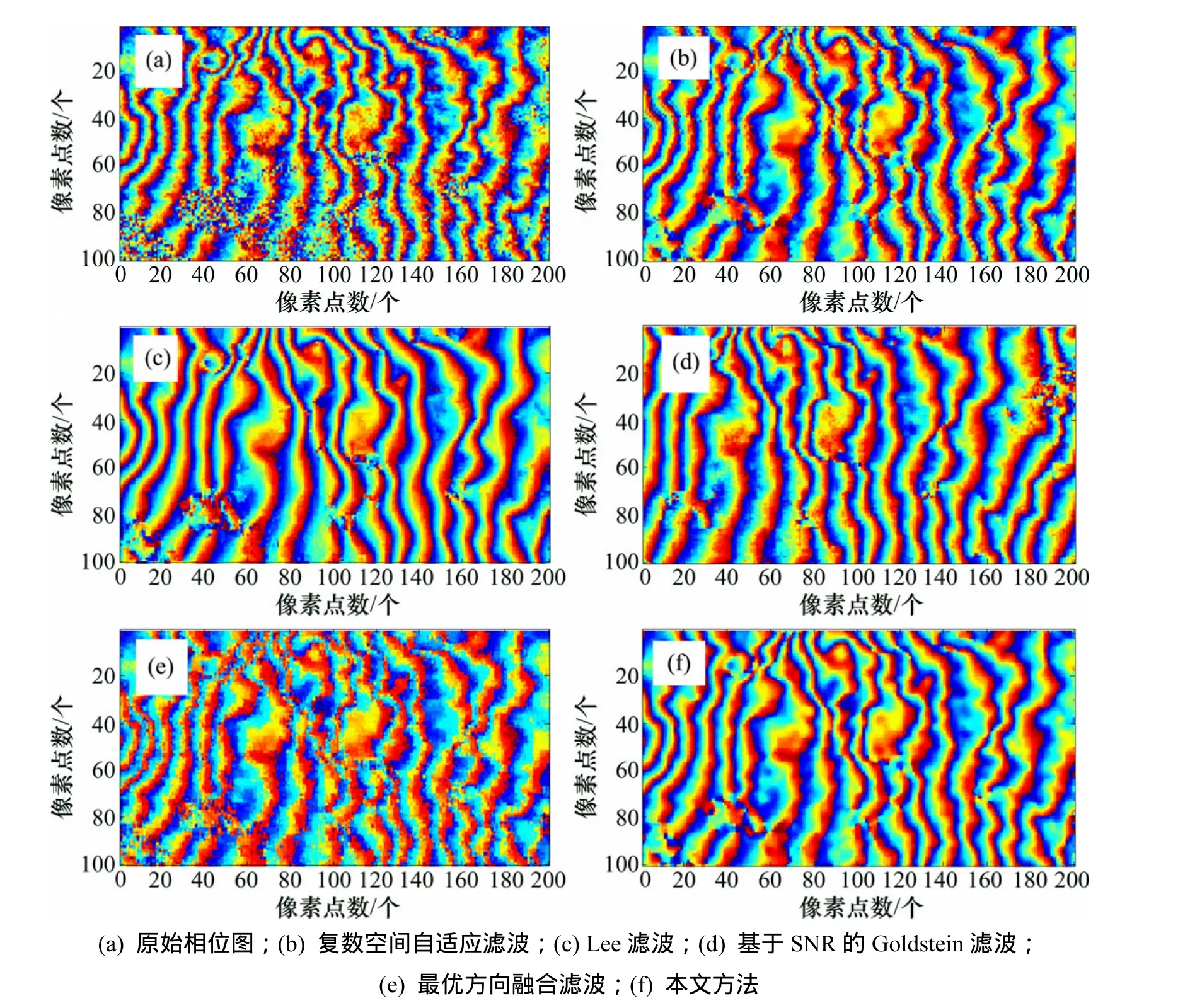
图8 意大利Etna火山截取干涉图滤波结果Fig.8 Filtering results of interferogram over part of Etna volcano in Italy

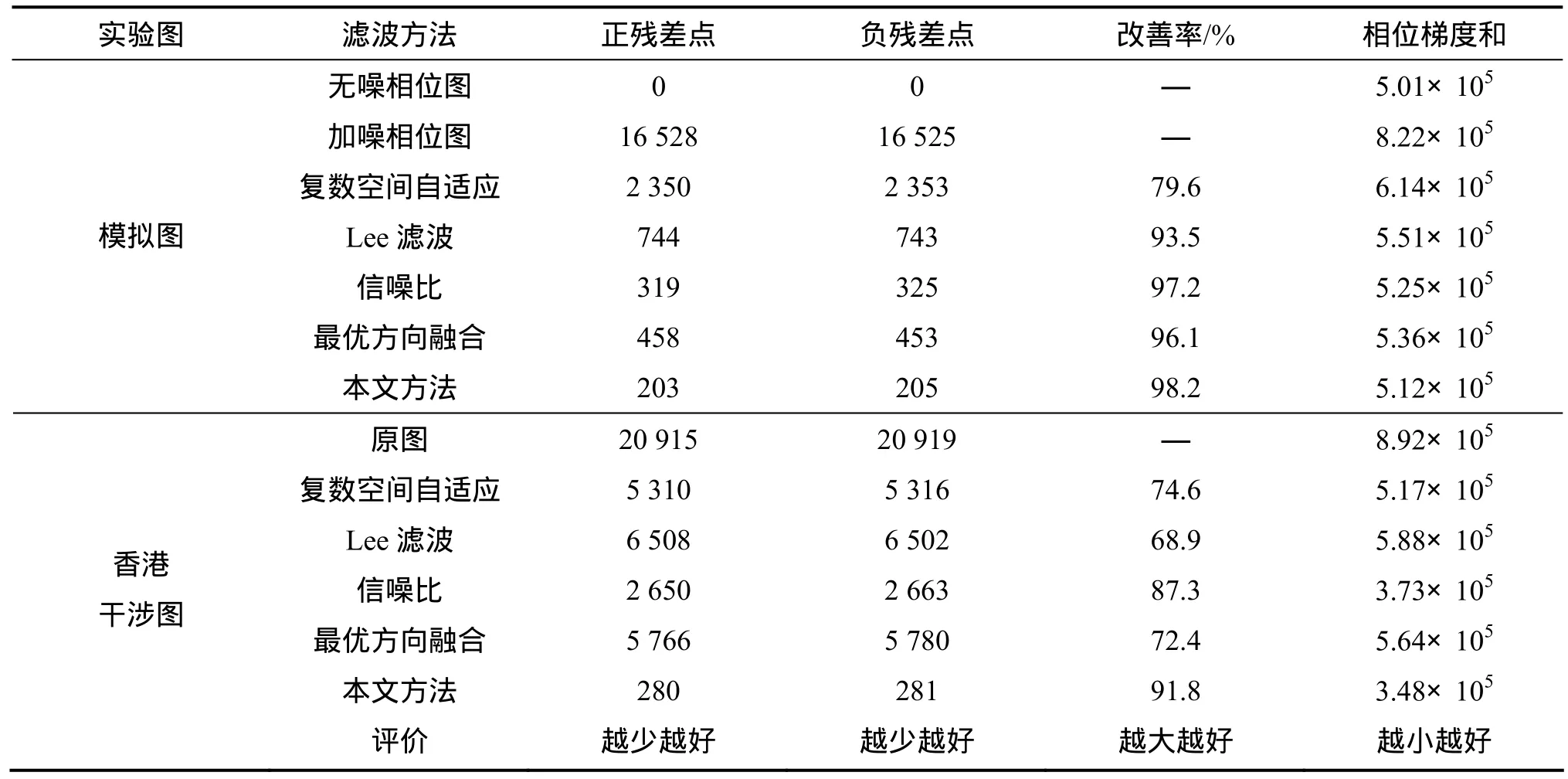
表1 干涉图滤波结果定量比较Table 1 Quantative comparison among filtering results of simulated interferogram

仍以模拟图和香港干涉图为例，用残余点数、相位梯度和(简称为SPD)对上述5种滤波方法进行定量评价，结果见表 1。模拟图的各种滤波方法的指标均较理想，而复数空间自适应滤波由于模拟图的噪声较多而受影响，残余点改善率稍低，说明kmax/3的尺度函数未能适应模拟图的噪声水平。从表1可知：虽然香港干涉图噪声不强，但由于真实噪声分布不均匀，随机性大，因而各项指标均有所下降。此处复数空间自适应滤波下降不大，说明该尺度函数更适应于香港干涉图，从侧面说明尺度函数应该随噪声水平而变。无论模拟图还是真实图，本文方法与复数空间自适应方法相比都有较大改善，且优于其他3种方法，模拟图残余点改善率由 79.6%提高到 98.2%，香港干涉图改善率由 74.6%提高到 91.8%，分别提高 18.6%和17.2%，说明本文方法更具有优势。

4 结论

(1) 复数空间自适应滤波的目的是找到与原始像素值相近的邻域像素尽可能参与平滑，因此，梯度小则认为该点与原始像素相近，相应地将其权重加大，与原始像素一起平滑；而梯度大则认为该点与原始像素不在同一条边缘上，将其权重减小，尽可能不参与平滑。实质上是给原始像素找到同质或相近点，并对这些点根据接近程度进行加权平均。

(2) 由于条纹走向有可能是斜方向，因此，考虑45°和 135°方向的梯度，可以更准确地判断原始中心像素与周围像素的关系，有助于找到遗漏的同质点，从而更合理地确定权系数。

(3) 噪声强弱决定滤波强弱，噪声可由干涉图相干系数表征，相干系数小时则噪声强，此时较大的尺度函数才能检测出条纹；相反，相干系数大时则噪声强，此时较小的尺度函数就能检测出条纹。因而加入相干系数的干预，使得复数空间自适应滤波的稳健性更强，局部自适应能力更强。

[1] Zebker H A, Villasenor J. Decorrelation in interferometric radar echoes[J]. IEEE Transactions on Geoscience and Remote Sensing, 1992, 30(5): 950-959.

[2] LI Zhiwei, DING Xiaoli, LIU Guoxiang. Modeling atmospheric effects on InSAR with meteorological and continuous GPS observations: Algorithms and some test results[J]. Journal of Atmospheric and Solar-Terrestrial Physics, 2004, 66: 907-917.

[3] Goldstein R M, Werner C L. Radar interferogram filtering for geophysical application[J]. Geophysical Research Letters, 1998,25(21): 4035-4038.

[4] Baran I, Stewart M P, Kampes B M, et al. A modification to the Goldstein radar interferogram filter[J]. IEEE Transaction Geoscience and Remote Sensing, 2003, 41(9): 2114-2118.

[5] LI Zhiwei, DING Xiaoli. Improved filtering parameter determination for the goldstein radar interferogram filter[J].ISPRS Journal of Photogrammetry and Remote Sensing, 2008,63: 621-634.

[6] 孙倩, 朱建军, 李志伟, 等. 基于信噪比的InSAR干涉图自适应滤波[J]. 测绘学报, 2009, 38(5): 437-442.SUN Qian, ZHU Jianjun, LI Zhiwei, et al. A new adaptive InSAR interferogram filter based on SNR[J]. Acta Geodaetica et Cartographica Sinica, 2009, 38(5): 437-442.

[7] 于晓歆, 杨红磊, 彭军还. 一种改进的 Goldstein InSAR干涉图滤波算法[J]. 武汉大学学报: 信息科学版, 2011, 36(9):1051-1054.YU Xiaoxin, YANG Honglei, PENG Junhuan. A modified Goldstein algorithm for InSAR interferogram filtering[J].Geomatics and Information Science of Wuhan University, 2011,36(9): 1051-1054.

[8] 靳国旺, 韩晓丁, 贾博, 等. InSAR干涉图的矢量分离式小波滤波[J]. 武汉大学学报: 信息科学版, 2008, 33(2): 132-135.JIN Guowang, HAN Xiaoding, JIA Bo, et al. Filtering for InSAR interferograms by vector decomposing and wavelet transformation[J]. Geomatics and Information Science of Wuhan University, 2008, 33(2): 132-135.

[9] 蔡国林, 李永树, 刘国祥. 小波-维纳组合滤波算法及其在InSAR干涉图去噪中的应用[J]. 遥感学报, 2009, 13(1):129-136.CAI Guolin, LI Yongshu, LIU Guoxiang. Wavelet-wiener combined filter and its application on InSAR interferogram[J].Journal of Remote Sensing, 2009, 13(1): 129-136.

[10] Loffeld O, Nies H, Knedlik S, et al. Phase unwrapping for SAR interferometry: A data fusion approach by Kalman filtering[J].IEEE Transactions on Geoscience and Remote Sensing, 2009,47(4): 1197-1211.

[11] Martinez-Espla J J, Martinez-Marin T, Lopez-Sanchez J M.Using a grid-based filter approach to solve InSAR phase unwrapping[J]. IEEE Transactions on Geoscience and Remote Sensing letter, 2008, 5(2): 147-151.

[12] Lee J S, Papathanassiou K P, Ainsworth T L, el al. A new technique for noise filtering of SAR interferogram phase images[J]. IEEE Transaction Geoscience and Remote Sensing,1998, 36(5): 1456-1465.

[13] 尹宏杰, 李志伟, 丁晓利, 等. InSAR干涉图最优化方向融合滤波[J]. 遥感学报, 2009, 13(6): 1099-1105.YIN Hongjie, LI Zhiwei, DING Xiaoli, et al. Optimal integration-based adaptive direction filter for InSAR interferogram[J]. Journal of Remote Sensing, 2009, 13(6):1099-1105.

[14] Mashaly A S, AbdElkawy E E F, Mahmoud T A. Speckle noise reduction in SAR images using adaptive morphological filter[C]//Intelligent Systems Design and Applications ISDA 2010 10th International Conference, Publisher: IEEE, 2010,41(3): 260-265.

[15] 王兴旺, 易辉伟, 朱建军, 等. 基于有选择保边缘平滑法的SAR干涉图像滤波算法[J]. 工程勘察, 2008(11): 50-53.WANG Xingwang, YI Huiwei, ZHU Jianjun, et al. A new phase noise reduction for INSAR interferogram based on edge-preservation smoother[J]. Geotechnical Investigation &Surveying, 2008(11): 50-53.

[16] Martinez-Espla J J, Martinez-Marin T, Lopez-Sanchez J M. An optimized algorithm for insar phase unwrapping based on particle filtering, matrix pencil, and region-growing techniques[J]. IEEE Geoscience and Remote Sensing Letters,2009, 6(4): 835-839.

[17] 郭交, 李真芳, 刘艳阳, 等. 一种InSAR干涉相位图的自适应滤波算法[J]. 西安电子科技大学学报, 2011, 38(4): 77-88.GUO Jiao, LI Zhengfang, LIU Yanyang, et al. New adaptive noise suppressing method for interferometric phase images[J].Journal of Xidian University, 2011, 38(4): 77-88.

[18] 李佳, 李志伟, 丁晓利, 等. 强噪声 SAR干涉图的等值线中值: Goldstein二级滤波[J]. 遥感学报, 2011, 15(4): 758-764.LI Jia, LI Zhiwei, DING Xiaoli, et al. Filtering strong noisy synthetic aperture radar interferogram with integrated contoured Median and Goldstein two-step filter[J]. Journal of Remote Sensing, 2011, 15(4): 758-764.

[19] Buemime, M E, Jacobo J, Mejail M. SAR image processing using adaptive stack filter[J]. Pattern Recognition Letters, 2010,31(4): 307-314.

[20] Lopez-Martinez C, Fabregas X, Pipia L. Forest parameter estimation in the Pol-InSAR context employing the multiplicative-additive speckle noise model[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2011, 66(5): 597-607.

[21] 廖明生, 林珲, 张祖勋, 等. InSAR干涉条纹图的复数空间自适应滤波[J]. 遥感学报, 7(2): 98-105.LIAO Mingsheng, LIN Hui, ZHANG Zuxun, et al. Adaptive algorithm for filtering interferometric phase noise[J].Journal of Remote Sensing, 2003, 7(2): 98-105.

[22] Franceschetti G, Lanari R. Synthetic aperture radar processing[M]. Florida: CRC Press, 1999: 185-190.