无速度传感器的动车组牵引电机控制算法
2013-09-20赵海波王有文于冰洋
赵海波,王有文,于冰洋
(中国北车集团 长春轨道客车股份有限公司 技术中心基础研发部,吉林 长春 130139)*
0 引言
目前的动车组牵引电机的控制算法中,速度信号都是通过在牵引电机的非驱动端安装的速度传感器获得的,但是在此位置安装传感器面临着工艺方面的困难,同时速度传感器的工作稳定性和电磁兼容问题同样困扰着我们,本文旨在通过建立无速度传感器的牵引电机矢量控制模型,为提高动车组的牵引电机控制算法提供一种新的理论支持,进而提高动车组的稳定性和可靠性.
1 牵引电机的控制
目前国际上最常用的动车组牵引电机控制技术有两种:矢量控制和直接转矩控制,我国的动车组普遍采用的是矢量控制[1].矢量控制的主要思想是将牵引电机的定子电流变换到以转子磁场定向的轴系中,经过力矩调节后,将控制量反变换到三相系统,经逆变器调节电机的定子电流和频率,实现对磁场电流和转矩电流的独立控制[2-3].
在三相坐标系下的定子交流电流ia、ib、ic通过3 s/2 s变换,可以等效成两相静止坐标系下的电流iα和iβ,再经过同步旋转变换,把电机定子电流分解成互相垂直的励磁电流iM和转矩电流iT.当观察着站在铁心上,并与坐标系一起旋转时,交流电机便等效成了直流电机.其中,交流电机的转子总磁通ψr就变成了等效的直流电机的磁通,M绕组相当于直流电机的励磁绕组,iM相当于励磁电流,T绕组相当于伪静止绕组,iT相当于与转矩成正比的电枢电流,这样,异步电机便等效成直流电机,因此,可以模仿直流电机的控制方法来实现对异步电机的控制,先求得直流电机的控制量,再经过相应的坐标反变换,就实现了异步电机的矢量控制[4-5].根据等效控制理论,可以构成直接控制ωr、ψr的矢量控制系统,如图1所示,其中iA、iB、iC为三相交流输入,ωr为转速输出[6].

图1 牵引电机矢量控制基本原理
2 牵引电机的矢量控制模型
2.1 磁链的数学模型
2.1.1 基于电压模型的方法
该方法的基本思想是利用检测得到的电机电压和电流,通过静止坐标系下的电机等效电路推导出来的方式来计算转子的磁链[7].
ds轴转子磁链 ψsdr的计算方程为
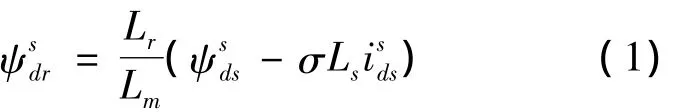
式中,Lr为转子电流;Lm为励磁电流;Ls为定子电流;σ为漏磁系数为ds轴定子电流;为ds轴定子磁链


式中,Lr为转子电流;Lm为励磁电流;Ls为定子电流;为qs轴定子电流;为qs轴定子磁链
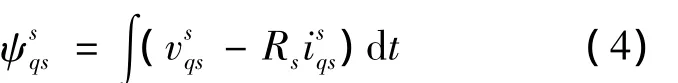
2.1.2 基于电流模型的方法
与基于电压模型方法的指导思想类似(通过静止坐标系下的电机等效电路推导),基于电流模型的方法是利用转速和电流信号来计算转子磁链,其方程式如下[8]:
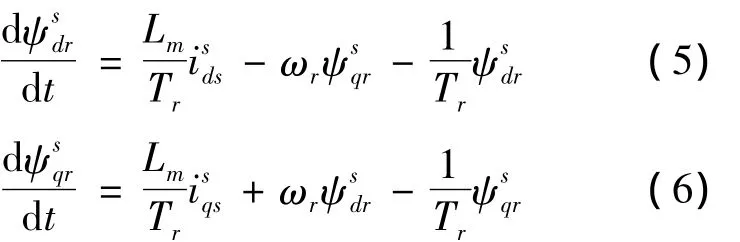
2.1.3 两种模型的比较
在动车组以低速运行时,也就是牵引电机低转速运行时,在这种情况下,通过第1种模型(基于电压模型的转子磁链模型)的准确性偏低,原因是低频时定子的电压很小,同时存在直流漂移;与此同时由于受温度的影响,定子和转子的电阻和电感等参数的变化也使模型的精度降低,但是基于电压模型的转子磁链模型在动车组高速段(也就是牵引电机高速运行时)的精度很好.与电压模型的转子磁链模型相比,基于电流模型的转子磁链模型可以在电机转速相对宽的范围内取得良好的精度[9].
2.2 转速的数学模型
建立转速的数学模型的主要思想是通过检测电机定子电流和电压值后计算得到其数值,具体计算方法很多,主要有模型参考自适应算法、卡尔曼滤波算法和神经元网络算法、应用模型参考自适用算法以及式(3)~(6),可以得到如下的转速数学模型[10]:

式(7)中 ωr为电动机的转速;,为按电流方程计算的转子磁链;ψrα和ψrβ为按电压方程计算的转子磁链.
3 实验结果
利用以上模型,通过仿真试验,可以得到图2、3所示的曲线.
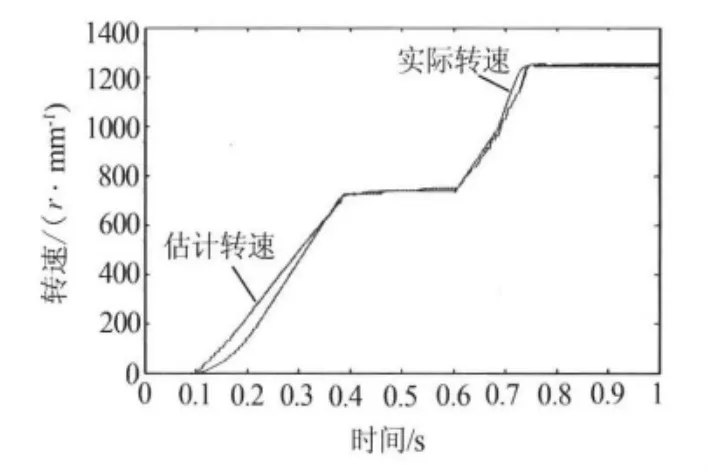
图2 实际转速和估计转速仿真结果
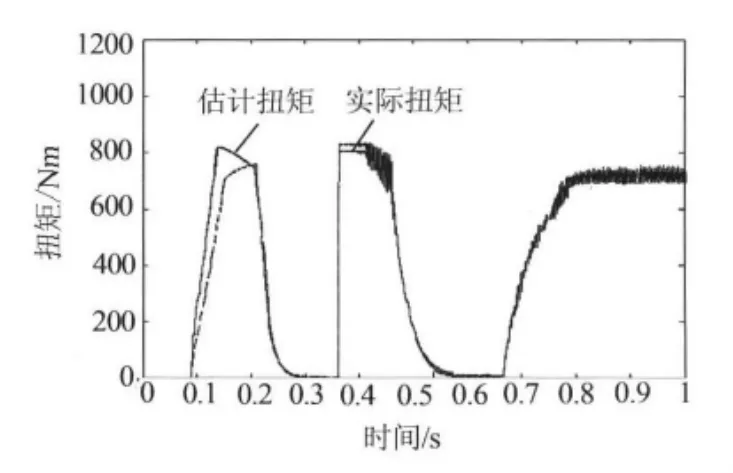
图3 实际扭矩和估计扭矩仿真结果
3.1 转速结果分析
从图2曲线中可以看到,在t=0.36 s之前,利用本文的算法,系统所得到估计转速和实际转速之间的误差在开始阶段较大,但是误差随时间逐渐减少至0,在0.36 s之后,估计转速和实际转速趋于一致(同时系统处于稳定阶段),在t=0.67 s时,估计转速与实际转速同步增大同时误差略有增加,在t=0.72 s时系统再次进入稳定阶段,估计转速和实际转速再次趋于一致.
3.2 扭矩结果分析
从图3曲线中可以看到,在t=0.36 s之前,利用本文的算法,系统所得到估计扭矩和实际扭矩之间的误差在开始阶段较大,但是误差随时间逐渐减少至0(在t=0.36 s时),估计扭矩和实际扭矩趋于一致,在t=0.67 s时,估计扭矩和实际扭矩同步增大(即估计扭矩能够随动态变化的扭矩信号同步变化),在t=0.72 s时系统再次进入稳定阶段,估计扭矩和实际扭矩再次趋于一致.
4 结论
通过对图2、图3的分析,可以得到以下结论:
(1)利用本文算法,能够在不依靠速度传感器的条件下对电机的转速和扭矩进行估计,并且能够在实际转速动态变化时同步变化,具有良好的估计精度和动态相应特性;
(2)利用本文算法,能够对动车组牵引电机矢量控制中的2个重要变量-转速信号和扭矩信号进行估计,并提供给控制器,实现在无速度传感器的条件下的高精度牵引电机矢量控制.
[1]李群湛.高速铁路电气化工程[M].成都:西南交通大学出版社,2006:31-40.
[2]BIMAL K Bose.现代电力电子学与交流传动[M].北京:机械工业出版社,2005:61-65.
[3]张川宝.齿轮传动比对动车组牵引特性的影响[J].大连交通大学学报,2011,32(4):79-82.
[4]冯晓云.交流传动及其控制系统[M].北京:高等教育出版社,2009.155-174.
[5]冯晓云.高速动车组牵引传动控制系统的研究与仿真[J].电气传动,2008(11):25-28.
[6]王英.异步电动机直接转矩控制磁链区间细分方法[J].大连交通大学学报,2011,32(4):83-87.
[7]BLASCO-GIME'NEZ R.Dynamic performance limitation for MRAS-based sensorless induction motor drives.Part 1:Stability analysis for the closed-loop drive[J].IEE Proc.on Electric Power and Applications,1996,143(2):88-95.
[8]王英.高压变频矢量控制系统的仿真[J].大连交通大学学报,2012,33(3):82-84.
[9]聂冰.交流电机调速系统的分数阶PID控制[J].大连交通大学学报,2012,33(3):77-80.
[10]徐传芳.五相混合式步进电动机恒频斩波恒总流驱动系统的稳态仿真[J].大连交通大学学报,2011,32(2):65-67.
