变速风力发电机组全局快速Terminal滑模控制
2013-09-20何真龚春英
何真,龚春英
(南京航空航天大学 自动化学院,江苏 南京 210016)
0 引言
风能是当今世界发展最快的新能源[1-3],风力发电技术成为了当前研究的热点。变速风力发电机组受到了很大的重视,它能够根据外界风速的变化而调整风机转速,以达到捕获最大风能或实现输出稳定功率的目的。
风能具有随机性和突发性的特点,风力发电机组模型具有很大的不确定性。滑模控制控制精度高,且滑动模态对系统的摄动和外部扰动具有较强鲁棒性[4]。普通滑模控制选取线性切换函数,在理论上不能保证系统状态在有限时间收敛到平衡原点;快速Terminal滑模控制以非线性函数构建滑模面以解决这个问题。本文将全局快速Terminal滑模控制应用于变速风力发电机组的控制。在引入Terminal滑动模态的基础上保留线性滑动模态,以提高收敛速度。针对系统不确定项的边界未知的现象,设计了边界估计算法。运用Lyapunov稳定性理论证明了系统稳定性。对机组在自然风和突变风下运行的情况进行了仿真。仿真结果验证了所设计的控制律的可行性,显示出较好的控制性能。
1 风力机组建模
图1为风电机组两质量块等效模型的示意图,图中Ta表示风机的机械转矩,Tg表示发电机的电磁阻转矩,J表示转动惯量,K表示传动系的刚性系数,B是传动系的阻尼系数,ω表示转速,下标r表示与风力机有关的量,下标g表示与发电机有关的量。可以写出机组传动系的动态方程[1-2]:


图1 风力机传动系结构图
直驱式机组中的风力机与发电机直接刚性相连,无需增速齿轮箱,可以近似认为传动轴无刚性扭转。因此直驱式机组中ωr=ωg,均用ω表示;不考虑刚性扭转,令刚性系数为0,从而由式(1)可以得到简化的风力发电机组的传动系统的数学模型:

式中B为系统的等效阻尼系数,B=Br+Bg;J为系统的等效转动惯量,J=Jr+Jg。
在风场中,定桨距风力机的输出气动转矩为:

式中ρ为空气密度,R为风轮机半径,v为风速,λ为风力机的叶尖速比,λ=,C为风力机的转矩系数,是关于叶尖速比λ的非T线性函数。
实际风机在运行过程中有一定的区域范围,通常采用二次多项式函数对该区域的转矩系数CT进行拟合,能保证拟合误差在很小的范围内[3,5],其形式如下:

其中λTmax为最佳叶尖速比,CTmax为最大转矩系数,kT为常系数。
风速v具有随机性,而且很难实时准确地测量,Ta具有不确定性,因而将式(2)中(Ta/J)当作不确定项,记为d,设|d| ≤L,L为未知的常数。
2 全局快速Terminal滑模控制
全局快速Terminal滑模控制以非线性函数构建滑模面,跟踪误差能在有限时间内收敛到平衡点。快速Terminal滑模控制无切换项,可以消除抖振。全局快速Terminal滑模控制既引入了Terminal吸引子,使得系统在有限时间内收敛,又保留了线性滑动模态,保证接近平衡状态的快速性。本节针对具有不确定性的风力发电机组,设计全局快速Terminal滑模控制律。引入具有递归结构的快速Terminal滑动模态为[6]:
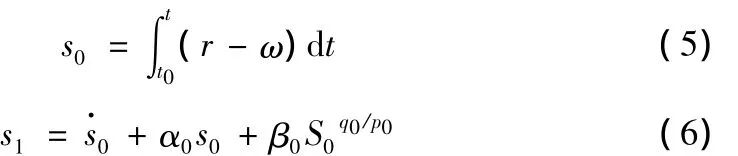
其中r为期望转速,系数 α0,β0>0,q0,p0(q0<p0)为正奇数。当ω远离r时,收敛速度由快速Terminal吸引子即决定,而当ω接近期望值r时,收敛速度主要由线性滑动模态决定,呈指数快速衰减。
风力机模型的不确定项d的边界为未知常数L,不能直接获得。设L的估计值为L^,其估计算法将在后面设计。令~L=L^-L,定义Lyapunov函数为:

对式(7)求导获得:

设计全局快速滑模控制律为:

其中 φ 为常数,γ=+η,η >0。
由式(2)、(8)和(9)得:

观察式(10)知,可设计估计算法为:

因此全局快速滑模控制律(9)和估计算法(11)作用下系统是稳定的。控制律(9)不含切换项,不会有抖振现象。
3 仿真与分析
风力发电机组的主要参数为:风轮机半径R为1.9 m,等效转动惯量J为0.39(kg·m2),等效阻尼系数为0.014 2(N·m·s/rad),CTmax为 0.07,KT为 0.01,λmax为 3.7。设计的全局快速滑模控制律和估计算法的参数取为:α0=2,β0=1,p0=9,q0=5,φ=100,τ=10。
首先对自然风场下的情况进行仿真。仿真中建立风速时间序列模型以模拟自然风场,模型包含基本风、渐变风、阵风和随机噪声风4个分量[7],风速曲线如图2(a)所示。期望转速在550 r/min和450 r/min之间每5 s切换一次。图2(b)为转速跟踪曲线,可以看出系统稳定,转速过渡平滑,2 s内即收敛到期望值,跟踪速度较快。
对机组在突变风速下的运行情况进行仿真。图3(a)为风速突变曲线,风速在13 m/s和17 m/s之间来回突变。图3(b)为机组的转速响应曲线。在风速突变这种较恶劣的工作条件下,转速变化非常小,控制器跟随性能优良,抗干扰性强。

图2 自然风速下仿真曲线
4 结束语
本文在建立风力发电系统的理论模型的基础上设计了全局快速Terminal滑模控制器。充分考虑风速的不确定性,设计了不确定项边界估计算法。引入 Terminal指数函数和线性函数结合构成的滑模模态。运用Lyapunov方法设计控制律并证明稳定性。对自然风速和较极端的突变风速下的运行情况进行了仿真,结果验证了系统的稳定性、较好的动态性能和较强的抗扰能力。

图3 突变风速下仿真曲线
[1] Beltran B,Ahmed-Ali T,Benbouzid M E H.High-order sliding-mode control of variable-speed wind turbines[J].IEEE Trans.Industrial Electronics,2009,56(9):3314 -3321.
[2] Beltran B,Ahmed-Ali T,Benbouzid M E H.Sliding mode power control of variable speed wind energy conversion systems.IEEE Trans.On Energy Conversion,2008,23(2):551-558.
[3]陈杰,陈冉,陈家伟,等.变速风力发电机组的模糊-单神经元PID控制[J].中国电机工程学报,2011,31(27):88-94.
[4] Nguyen H.M.,Subbaram N.D.Advanced control strategies for wind energy systems:An overview[C].IEEE Pes Power Ssystems Conference& Exposition(PSCE).PHOENIX,AZ,USA,2011.
[5] Fernando D B,Hernán B,Ricardo J M.Wind turbine control systems principles,modeling and gain scheduling design[M].Springer,2006.
[6]刘金琨.滑模变结构控制MATLAB仿真[M].北京:清华大学出版社 ,2005.
[7]张红光.大容量风电并网对电力系统安全稳定的影响[D].保定:华北电力大学,2008.
