高温填充床相变储热球的储热特性

李 传，孙 泽,2，丁玉龙,3

（1英国利兹大学过程环境材料学院，英国 利兹 LS2 9JT；2华东理工大学资源与环境工程学院，上海 200237；3中国科学院过程工程研究所，北京 100190）

太阳能作为一种清洁、可持续、普遍的能源，近年来得到了广泛的关注。据统计，太阳辐射到地球上的资源总量相当于人类现在所用能源的一万多倍。然而其能量密度低，而且因地而异，因时而变，世界上很多地方每年的太阳能直接利用时间在2000 h以下，这远远不能满足人们对太阳能利用的需求。因此，发展高效储热技术，强化太阳热能的转换效率和存储密度，成为太阳能高温利用的关键技术之一[1-6]。

在常见的显热、潜热及化学储热这三种储热方式中，基于相变材料（PCM）的潜热存储因具有储热密度大及结构紧凑等优点，在太阳能热能储存、核能和常规电力“移峰填谷”等领域具有巨大的应用前景[7-12]。填充床相变储热系统是相变储热技术中一种相对成熟且简单的储热和换热设备，近年来出现了较多对其相变储热性能的报道[13-15]。郭茶秀等[16]选取填充床系统中的储热单元球为研究对象进行了模拟研究，考察了热传导对其传热性能的影响规律。Xia等[17]开发了一种有效的填充床模型，并通过该模型对填充床储热系统传热性能进行了模拟研究，同时与文献中的实验数据进行了对比。赵岩等[18]采用不同的储热材料，对填充床储热系统的储热特性进行了模拟研究，并考察了热分层和相间温度差对储热性能的影响规律。李萍等[19]利用自行设计的填充球蓄热室模拟系统，考察了蓄热室、相变球性能参数和外界操作参数对填充球蓄热室热效率的影响规律。

这些文献中对填充床储热系统的研究主要集中在低温领域，其相变材料相变温度普遍低于120 ℃[12-15]，而对高温领域（相变温度高于300 ℃）很少涉及，尤其是能应用于高温太阳能热储存利用领域的研究更少。为此，本工作基于高温相变储热材料，以填充床储热系统中的储热单元球为研究对象，对其储热性能进行模拟研究。研究了不同传热流体温度和球体直径对储热性能的影响规律，对单纯导热为主的相变储热与导热和自然对流共同作用的储热过程进行了比较分析，同时还探讨了高温辐射换热、导热及自然对流耦合对球体储热性能的影响，为高温填充床储热系统的研究提供基础。

1 数学模型

1.1 物理模型

图 1(a)为高温填充床储热系统结构示意图。不锈钢金属储热单元球体处于垂直筒体中，球体中密封着相变材料。传热流体流经床体时，与储热单元球体发生热交换。由于流体在床体中的流动经常改向，导致传热过程的强化。本文研究对象的“储热单元球体”物理模型如图1(b)所示，考虑直径（D）为30、40、60、70 mm的球体为模拟研究对象。

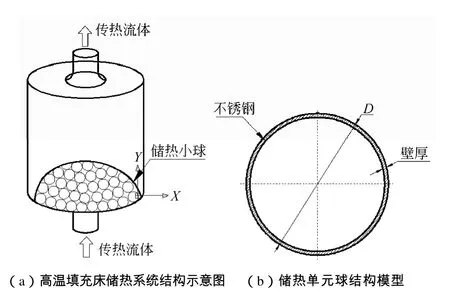
图1 填充床储热系统和储热单元球结构模型Fig.1 Schematic diagram of a packed bed energy storage unit and structure of a spherical packed particle

1.2 数学模型

本文使用焓-孔隙率模型来处理相变材料的熔化/凝固过程，相变计算区域被分为固相、液相和混合相三个区域，通过液相率（γ）来间接地跟踪相界面位置的变化，液相率的计算基于焓的平衡求解，同时在动量方程中加入合理源项来计算由于固相材料的存在而产生的压降。

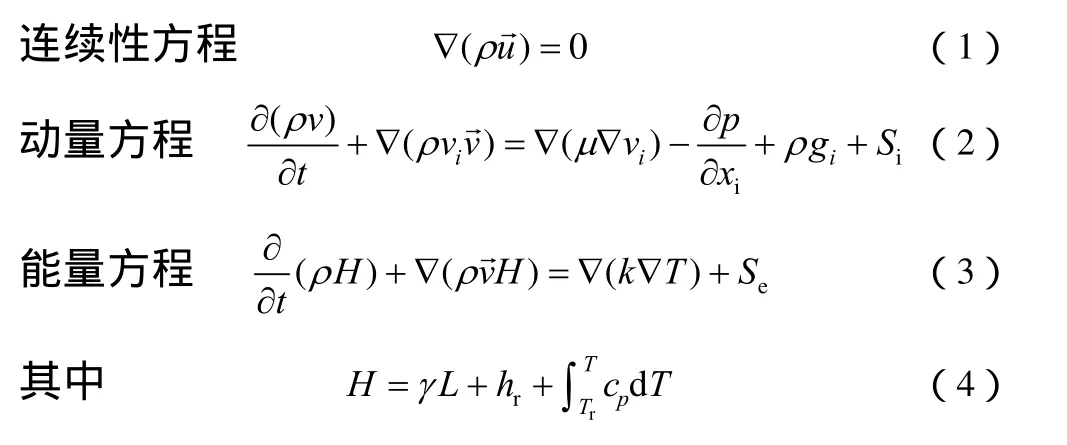
式中，H为相变材料总焓值；ρ为相变材料密度；v→为液相速度；Se为能量方程源项；vi为速度分量；P为压强；hr为相变材料的参考焓值；L为相变潜热；Cp为比热容；μ为液相黏度；γ为液相率，其值在0～1之间变化；当PCM 温度小于熔化温度时，γ=0，PCM为固相；当PCM温度等于熔化温度时，0<γ<1，PCM为固液两相共存；当PCM温度大于熔化温度时，γ=1，PCM为液相。Si为动量方程源项，具体表示为

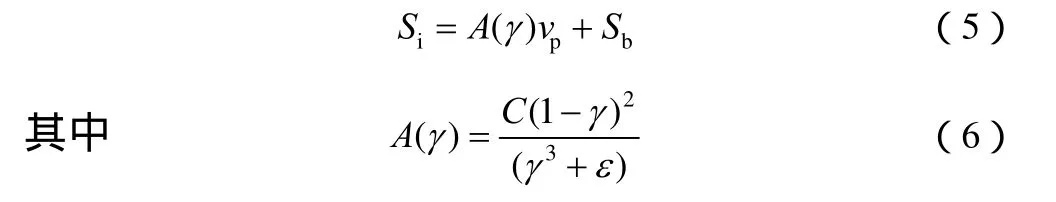
式中，A(γ)为多孔介质流动的Carman-Kozeny函数；ε=0.0001是一个很小的计算常数；vp为随着熔化进行固相脱离模糊区的牵引速度；常数C反映相变前沿的形态，常取值为10～10；Sb表示浮力项，其处理方法是采用Boussinesq假定，除浮力项外所有项中的密度可认为恒定，浮力项中的密度随温度呈线性变化。

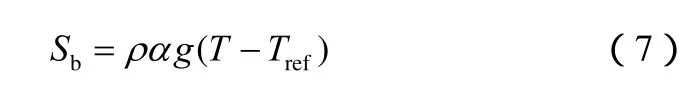
式中，α为相变材料的体积膨胀因子，K-1；Tref为初始温度，K。

辐射模型采用 Rosseland辐射模型。由于加入辐射传热，能量方程中的源项需要添加辐射源。该辐射源项表达式为

式中，k为导热率；a为吸收系数；σs为散射系数；σ为斯蒂芬-波尔兹曼常数；C为线性各相异性相位函数系数。

2 模拟计算结果与分析

2.1 边界和初始条件

本文选取相变材料及封装材料的物性参数如表1所示。计算过程中取边界条件为定温边界条件，初始温度为523 K。此外，对模型做如下假设：① 忽略球壁厚度；② 相变材料只有一个熔点；③ 相变材料固液两相的比热容、导热系数、密度为常数，不随温度发生变化，且各向同性；④ 满足Boussinesq假设，只在浮力项中考虑密度变化，浮力项中密度随温度呈线性变化。

表1 相变材料和封装材料的物性参数Table 1 The physical parameters of PCM and encapsulation material

2.2 热传导传热条件下的储热性能

本节考察单纯热传导传热条件下的球体储热性能。虽然在实际的应用中，球体内热量的传递不仅仅局限于热传导，但作为后续研究自然对流等的影响规律，理解纯热传导条件的现象很有必要。图2、图3为不同球体直径和传热流体温度对储热性能的影响。如图2所示，当传热流体温度一定时，不同直径储热球体内相变材料完全相变所需要的时间不同。当传热流体温度设定为793 K时，随着球体直径的增大，完全相变所需要的时间也随之增大。直径为30 mm的球体完全相变需要时间为470 s，而当直径增大为70 mm时，对应的完全相变时间增大到2550 s。图3为球体直径一定时，传热流体温度与相变时间的关系。取直径为40 mm的球体为研究对象，如图3所示，随着传热流体温度的增加，完全相变的时间也随之缩短。这是因为在以纯导热为主的传热过程中，储热球表面传热温差的增大，传热量也随之增加，因而完全相变时间缩短。

图2 球体直径对相变时间的影响Fig.2 Time evolution of liquid fraction as a function of time for different sized particles

图3 流体温度对相变时间的影响Fig.3 Time evolution of liquid fraction as a function of time for different heat transfer fluid temperatures

2.3 自然对流对储热性能的影响

本节在2.2节研究单纯热传导影响的基础上，使用Boussinesq模型来考虑自然对流对球体储热性能的影响。以直径40 mm的球体为研究对象，传热流体温度设定为793 K。图4为考虑自然对流与不考虑自然对流影响时，球体内液-固界面随时间变化情况的对比图。对比图4(a)和4(b)可以看出，考虑自然对流的影响时，球体内相变不再是沿球心的对称运动。相变刚开始时液相的成分较小，球体内主要以导热为主。随着相变过程的进行，液相比率逐渐增大，由浮力引起的自然对流加强。由图 4(a)可以看出，在重力的作用下，固相相变材料会向下运动，熔化过程是不对称的。同时，相变材料相变过程中体积膨胀产生的压力也会加速固相材料的下沉，从而加大了自然对流的影响。不考虑自然对流影响时，完全相变时间为850 s左右；考虑自然对流影响时，相变时间缩短为720 s左右，时间缩短了近16%。图5比较了液相率随时间的变化情况，可见自然对流的影响主要在相变过程的后期。

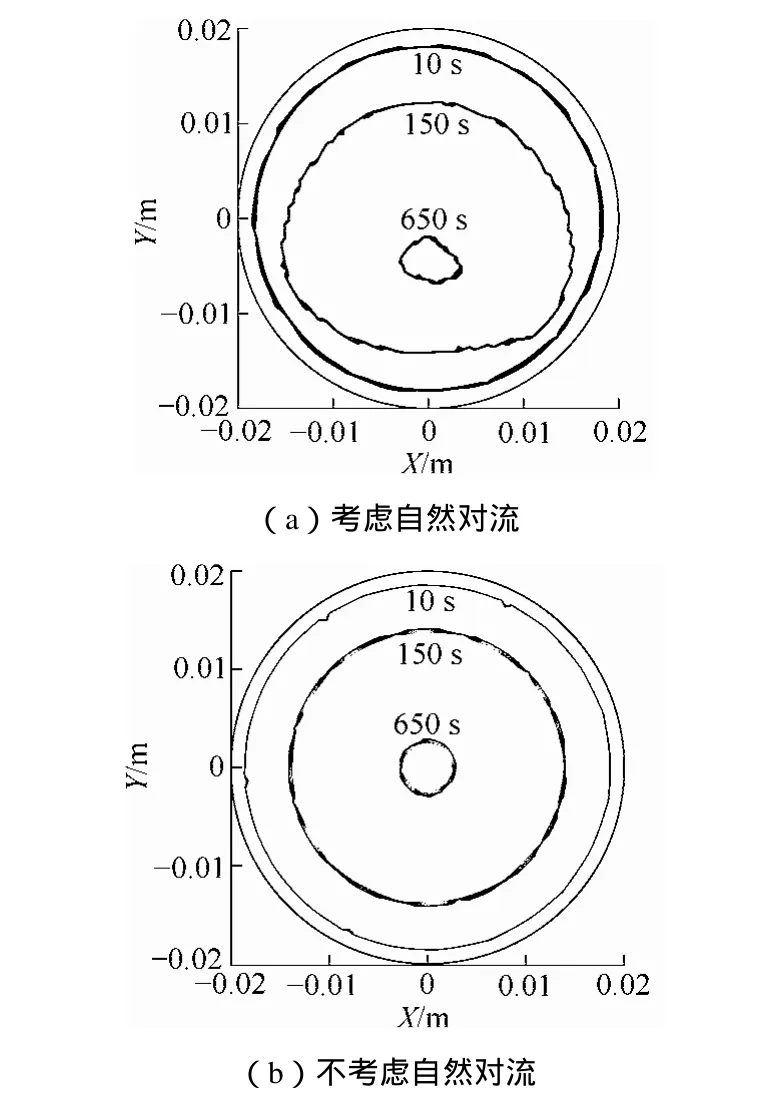
图4 不同熔化时间的液固相变界面Fig.4 Time evolution of liquid-solid interface with (a)and without natural convection (b)

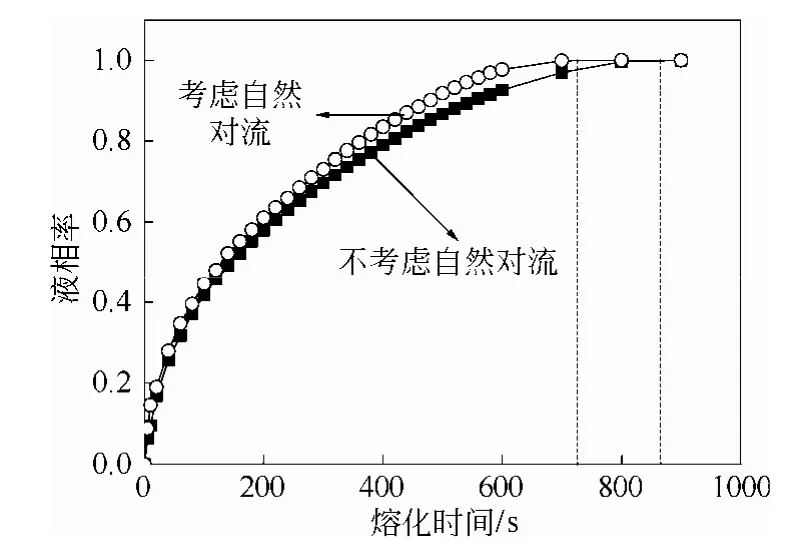
图5 液相比率随熔化时间的变化关系Fig.5 Liquid phase fraction as a function of time

2.4 热传导、自然对流模型验证

为了验证本工作对热传导和自然对流模拟方法和结果的准确性，以文献[20]中的实验装置为物理模型，采用与文献中相同的相变材料进行了相同的模拟研究。这里的相变材料为 NaOH，其熔化热为200 kJ/kg，导热系数为0.5 W/(m·K)，密度为2257 kg/m3，平均比热容为1486J/(kg·K)，熔点为588.75 K。传热流体为三元硝酸熔融盐流体，其导热系数为 0.571 W/(m·K)，平均比热容为 1.51 kJ/(kg·K)，密度为1860 kg/m3，黏度为0.0032 m2/s。模拟结果如图6所示，直管完全相变时间为1300 s左右，弯管完全相变的时间为1000 s左右；模拟结果（实心线）与文献[20]中结果（实心和空心点）一致。

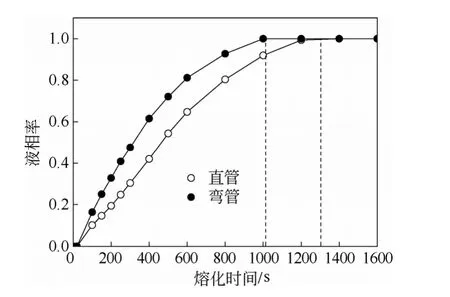
图6 NaOH液相率随时间的变化Fig.6 Liquid fraction of NaOH as a function of time

2.5 辐射换热边界条件对储热性能的影响

辐射换热是高温条件下换热的重要方式，在高温换热过程中，必须考虑辐射换热。本文研究对象为高温填充床储热单元系统，相变材料相变温度为581 K，传热流体温度为800 K左右，在实际的相变过程中，辐射换热量不容忽视。因此本节在之前研究的基础上，选取直径为40 mm的球体为研究对象，考察辐射换热、热传导及自然对流耦合对球体储热性能的影响。

图7为熔化时间为10 s时，考虑辐射换热和不考虑辐射换热两种情况下球体内的温度分布。可以看出，考虑辐射换热时，相变材料的熔化速度较快，球体内的温度明显要高于不考虑辐射换热时的温度。分析图 7(b)还可以看出，顶部的温度要高于底部的温度，球体内出现了自然对流，在自然对流的作用下，球体内温度呈不对称分布。可见辐射换热加速了自然对流作用的出现，从而加强了球体内的传热过程，并进而加快了相变材料的熔化速度。

图7 熔化时间为10 s时的温度对比Fig.7 Comparison of temperature distributions with and without radiation effect (10 s)

图8为熔化时间为100 s时球体内的液相比率和速度场的分布。可以看出，球体内的相变过程与自然对流作用下的相变过程类似。随着相变过程的进行，液相比率的增大导致由浮力引起的自然对流加强。在重力和浮力的作用下，固体相变材料会向下运动，球体左右边壁的速度梯度比较大。球体内的传热由外部的热辐射和内部的热传导耦合为主转变为外部的热辐射和内部的自然对流耦合为主。由图7和图8可以看出，辐射换热对球体内温度分布有较大的影响，加快了相变材料的熔化，强化了自然对流。相比较纯导热和自然对流，相变区域内的传热过程得到了强化。

本文在研究导热和自然对流影响的基础上，考虑了辐射换热的影响，文中选取的辐射计算模型是对辐射换热影响的初步探索，对于不同辐射计算模型的的优化选择与相关实验验证还有待进一步的展开。

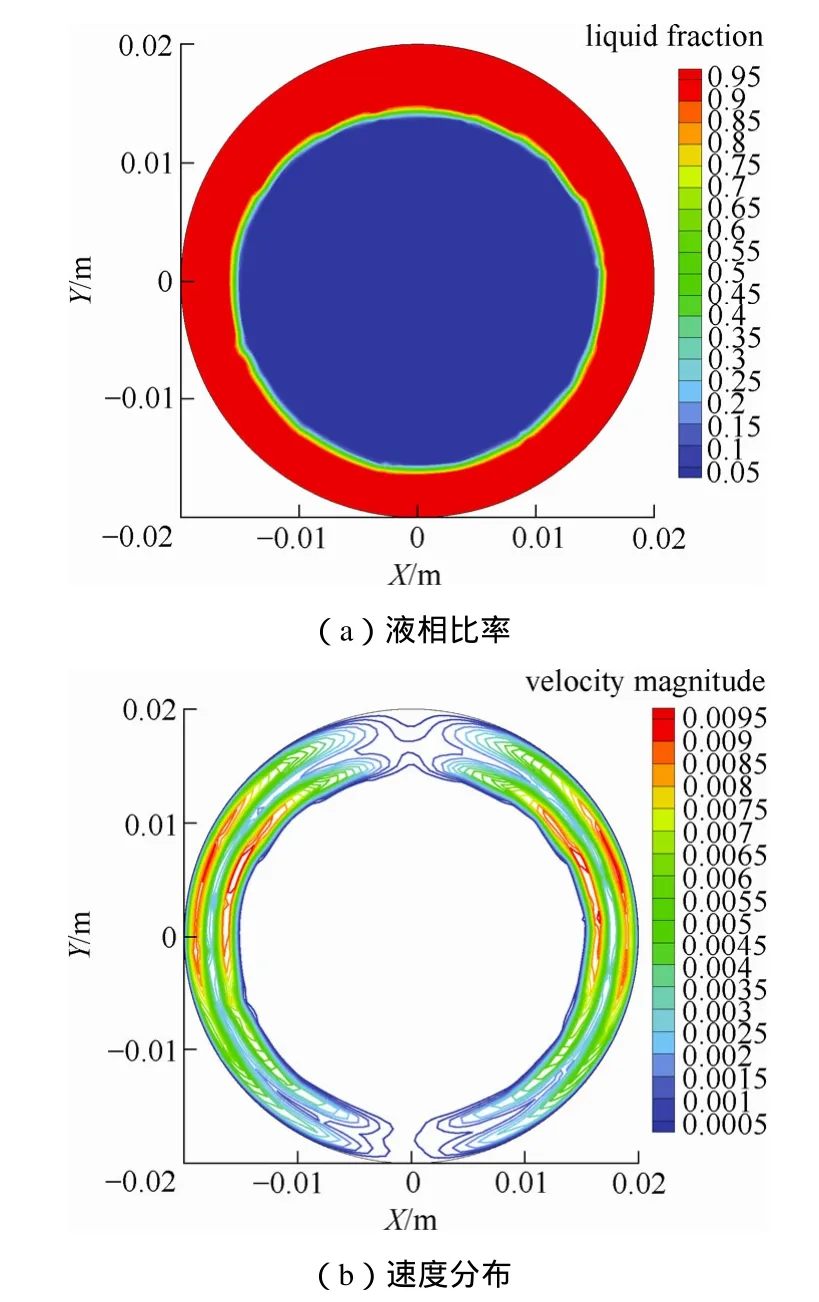
图8 100 s时的液相比率和速度场分布Fig.8 Distributions of liquid fraction (a)and velocity (b) at 100s

3 结 论

（1）球体结构尺寸和传热流体温度对球体储热性能有较大的影响。传热流体温度一定时，完全相变所需要的时间随球体直径的增大而增大。球体直径一定时，完全相变所需要的时间随传热流体温度的增大而减小。

（2）考虑相变区域自然对流的影响时，总的相变时间显著减少，和纯热传导相比，完全相变时间缩短了近16%。随着相变过程的进行，液相比率的增大，相变不再是沿球心的对称运动，在重力和浮力的作用下，相变过程变得不对称，固相相变材料向下运动，同时，相变材料相变过程中体积膨胀产生的压力也加速固相材料的下沉，从而加大了自然对流的影响。

（3）外部辐射换热对球体内温度分布有较大的影响，强化了自然对流，加快了相变材料的熔化。相比较纯导热和自然对流，相变区域内传热过程得到了强化，在研究高温储热系统时，辐射换热的影响不容忽视。

[1] Zuo Yuanzhi（左远志），Yang Xiaoxi（杨晓西），Ding Jing（丁静），et al.熔融盐中高温斜温层混合蓄热方法及装置：CN，200710028077.X[P]. 2008-12-24.

[2] Kearney D，Herrmann U，Nava P，et al.Assessment of a molten salt heat transfer fluid in a parabolic trough solar field[J].Journal of Solar Energy Engineering，2003，125（2）：170-176.

[3] Singh H，Saini R P，Saini J S.A review on packed bed solar energy storage systems[J].Renewable and Sustainable Energy Reviews，2010，14（3）：1059-1069.

[4] Farid M M，Khudhair A M，Razack S K A，Al-Hallaj S.A review on phase change energy storage：Materials and applications[J].Energy Conversion & Management，2004，45（9-10）：1597-1615.

[5] Verma P，Varun，Singal S K.Review of mathematical modeling on latent heat thermal energy storage systems using phase-change material[J].Renewable and Sustainable Energy Reviews，2008，12（4）：999-1031.

[6] Evans A，Strezov V，Evans T J.Assessment of utility energy storage options for increased renewable energy penetration[J].Renewable and Sustainable Energy Reviews，2012，16（6）：4141-4147.

[7] Bindra H，Bueno P，Morris J F，Shinnar R.Thermal analysis and exergy evaluation of packed bed thermal storage systems[J].Applied Thermal Engineering，2013，52（2）：255-263.

[8] MacPhee D，Dincer I.Thermal modeling of a packed bed thermal energy storage system during charging[J].Applied Thermal Engineering，2009，29（4）：695-705.

[9] Regin A F，Solanki S C，Saini J S.Heat transfer characteristics of thermal energy storage system using PCM capsules：A review[J].Renewable & Sustainable Energy Reviews，2008，12（9）：2438-2458.

[10] Karthikeyan S，Velraj R.Numerical investigation of packed bed storage unit filled with PCM encapsulated spherical containers—A comparison between various mathematical models[J].International Journal of Thermal Sciences，2012，60：153-160.

[11] Erek A，Dincer I.Numerical heat transfer analysis of encapsulated ice thermal energy storage system with variable heat transfer coefficient in downstream[J].International Journal of Heat and Mass Transfer，2009，52（3-4）：851-859.

[12] Zuo Yuanzhi（左远志），Yang Xiaoxi（杨晓西），Ding Jing（丁静）.Heat transfer performances of high-temperature shell-tube heat exchanger with molten-salt phase change materials[J].Journal of South China University of Technology（华南理工大学学报），2011，39（12）：42-47.

[13] Eduard O，Justin C，Viktoria M，Cabeza L F.Comparative study of different numerical models of packed bed thermal energy storage systems[J].Applied Thermal Engineering，2013，50（1）：384-392.

[14] Regin A F，Solanki S C，Saini J S.An analysis of a packed bed latent heat thermal energy storage system using PCM capsules：Numerical investigation [J].Renewable Energy，2009，34（7）：1765-1773.

[15] Wu S M，Fang G Y，Liu X.Thermal performance simulations of a packed bed cool thermal energy storage system using n-tetradecane as phase change material[J].International Journal of Thermal Sciences，2010，49（9）：1752-1762.

[16] Guo Chaxiu（郭茶秀），Xiong Huidong（熊辉东），Wei Xinli（魏新利），et al.Numerical research on solidification of cooling storage ball by FLUENT[J].Energy Conservation Technology（节能技术），2005，23（134）：488-491.

[17] Xia L，Zhang P，Wang R Z.Numerical heat transfer analysis of the packed bed latent heat storage system based on an effective packed bed model[J].Energy，2010，35（5）：2022-2032.

[18] Zhao Yan（赵岩），Wang Liang（王亮），Chen Haisheng（陈海生），et al.Analysis on thermal storage characteristic of sensible and latent heat in packed beds[J].Journal of Engineering Thermophysics（工程热物理学报），2012，33（12）：2052-2057.

[19] Li Ping（李萍），Zeng Lingke（曾令可）.Numerical analysis for heat efficiency of ball packed-bed regenerator[J].Industry Heating（工业加热），2008，37（5）：19-22.

[20] Wang Peilun（王培伦），Peng Zhijian（彭志坚），Wang Shuhao（王述浩），et al.Numerical simulation of heat transfer behaviour of a twisted pipe containing a phase change material[J].Energy Storage Science and Technology（储能科学与技术），2012，1（2）：116-122.