基于互样本熵的脑电功能网络构建及其应用

冯志燕，郭志鹏，罗回春

（西安电子科技大学 生命科学技术学院，陕西 西安 710071）

大脑是人体最重要的是器官之一，是中枢神经系统的主要组成部分。大脑是人体接受外界刺激并做出反应、产生思维和意识的中枢，一直以来，人类都在不停的探索大脑的奥秘，从理论思考探索到临床解剖再到近年来的计算机断层扫描、脑电图、核磁共振成像、正电子发射扫描等[1]，对于大脑的研究方法在不断地提升和改进，关于大脑生理活动的研究也在不断深入。

脑电地形图是在脑电图的基础上，通过对所采集各节点的脑电信号进行快速傅里叶变换后，得到δ、θ、α、β 4个波段的重组信号，再分别计算每组信号的功率谱密度值，再以大脑平面为基础，功率谱密度值为灰度值，通过插值所画出四个波段的图形。由于脑电地形图较脑电图更为直观，并且无创、无痛、无副作用，因此它在临床上具有重要的诊断价值和广阔的前景。就目前而言，脑电地形图在对于各种脑血管疾病、精神类疾病的检测和判断都具有相当重要的作用。

随着大脑神经功能性连接网络和结构性网络的研究证实了脑网络具有小世界特性，关于复杂脑网络的研究也成为了脑电科学研究的一个重要的方向[2]。此外，复杂脑网络理论也为脑电图（EEG）、脑磁图（EMG）、功能核磁共振成像（fMRI）等技术提供了新的分析手段，丰富了脑电科学的内容[3]。功能性网络是指节点之间的信号在同一时间内在统计意义上的关系。文中就是据此来研究脑电图信号之间的关系，得到各通道间的网络关系。具体做法是：以电极所在区域为节点，量化各节点信号之间的关系，再确定阈值，得到各电极所代表区域的功能连接强度，构建功能性脑网络。

1 研究方法

1.1 小波变换

小波包变换能够对频带部分进行多层次划分，是一种对于低频信号和高频信号都能够提供精细的、无冗余的分解和重构，并且能够包含大量的细节信息。在信号分析方面可进行滤波、去噪声、压缩、传递等处理。关于小波变换的具体定义与算法请参阅相关参考文献[4]。

将待分析的脑电信号导入到Matlab中，对每个通道的信号逐一采用小波基‘db4’进行8个尺度的小波包分解，得到层数为8的小波分解树。由于脑电信号的采集频率为500 Hz，则奈奎斯特频率为250 Hz，所以经小波包分解后，每一节的频率为 250/28=0.976 6 Hz。 在这之后按照 δ波（1～4 Hz）、θ波（4～7 Hz）、α 波（8～12 Hz）、β 波（13～30 Hz）的标准来重构脑电信号，具体分解如图1所示。

1.2 互样本熵

互样本熵的概念是根据样本熵的概念而提出的，是对样本熵算法的拓展。在实际应用中互样本熵只需要较少的数据量就可以对所给数据得到一个较为稳定的估计值。有较好的抗噪声能力和抗干扰能力，其分析效果优于简单统计参数，适合对生物信号进行分析[5]。

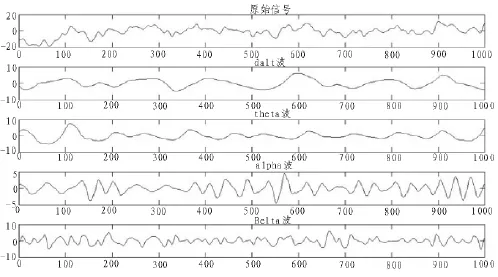
图1 原始脑电的小波分解Fig.1 Wavelet decomposition of the raw EEG

互样本熵通常是以如下的方式定义的[6]：

1）将序列{u（i）}按顺序组成 m 维的矢向量 X（i），即：

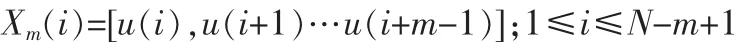
2）对每一个 i值计算矢量 X（i）与其余矢量 X（j）之间的距离：

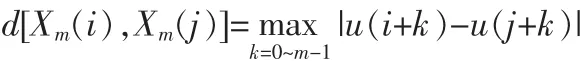
式中：0≤k≤m－1，1≤i，j≤N－m+1

3）给定阈值 r（r＞0），对每一个 1≤i≤N－m+1 的值统计 d[Xm（i），Xm（j）]＜r的数目及此数目与总的矢量个数 N－m+1 的比值，记作（r）即

其中 1≤j≤N－m+1，j≠i

对所有i求平均值

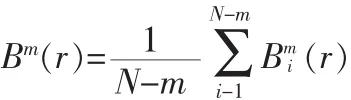
4）再对 m+1，重复 1）～3）的过程，得到 Bm+1（r）。

5）Bm（r）和 Bm+1（r）分别是当维数是和时两序列的相似概率，记作样本熵为H，则理论上序列的样本熵为：

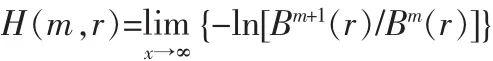
当N为有限值时，可得序列长度为N时样本熵的估计值为：

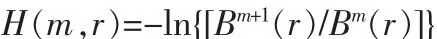
通过参照以上样本熵的概念，将第二条定义中的其余矢量 X（j）换成一个新的矢向量 Y（i），Y（i）=[v（j），v（j+1），…v（j+m－1）]；1≤i≤N－m+1， 再通过后续运算即可得到序列 u 和序列v之间的互样本熵[5]。

2 数据采集

本实验采用Neurotropic NT9200脑电放大器 （北京中科新拓仪器公司，中国）来采集脑电信号，使用32通道的记录电极，电极标号依次为 FP1、FP2、F3、F4、C3、C4、P3、P4、O1、O2、F7、F8、T3、T4、T5、T6、Fz、Cz、Pz、Fc3、Fc4、Cp3、Cp4、Ft7、Ft8、Tp7、Tp8、FCz、CPz、Oz、Pg1、Pg2。 按国际标准 10－20 系统法放置导联位置，头皮接触阻抗小于3 kΩ，采样率设置为1 000 Hz，频带设置为0.8～70 Hz，50 Hz陷波启用。

数据记录时所有受试者均被要求静坐在椅子上，闭眼休息，采集时长5 min。本实验选取择无明显噪声的连续2 s的2 000个数据，在这2 000个数据选用奇数位的1 000个数据（采样频率为500个/秒）作为实验分析对象。

本实验正常人数据共有12组，全部取自没有精神病史的在校研究生，其中男10名，女2名；左利手1名，右利手11名；年龄23～26岁，平均年龄24.4岁。癫痫症患者1名，精神分裂症患者1人，抑郁症患者1人。实验开始前，所有受试者均被告知实验的目的和内容，并签署受试者知情同意书。

3 结 果

将32个通道的脑电信号两两之间的互样本熵计算出来，以大脑表面为平面，电极所在位置为节点，每个通道和其他所有通道的互样本熵总和为图像的灰度值，再通过插值绘出δ、θ、α、β 4 个波段的脑电地形图。

选取精神病患者、抑郁症患者和正常人的脑电信号，分别计算其各自的互样本熵，得到各自基于互样本熵的脑电网络地形图。

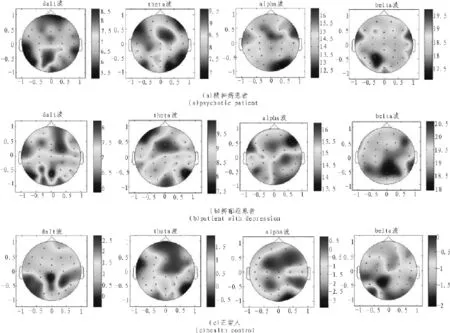
图2 不同人的互样本熵脑电网络地形图示例Fig.2 Cross-sample entropy network mapping of brain electrical activity

从实验结果可以看出，精神病、抑郁症等脑部疾病在我们所绘制的脑电网络地形图上都有相应的反映，并且可以对脑电波进行多种方式的反映，在反映的精度和准确度上都要比传统的脑电地形图提高很多。

4 结 论

文中提出了一种采用互样本熵分析处理脑电信号的方法，相比于通过节点度、聚类系数、节点介数等方法来建立功能网络，该方法明显缩短了数据数量，只需要很短的数据量就可以得到稳健的估计值，并采用了小波包分解重构信号的方法，提高了信号的抗干扰和抗噪能力，是一种非线性的分析方法[6]。限于条件限制，参加脑电数据采集实验的患者还不够多，在以后的工作中将进一步增加病例数目，更好地研究静息态脑网络的统计特性。文中提出的方法相信可以成为一种和聚类系数、节点介数等一样用于分析脑电信号、建立脑功能网络的重要手段，对于脑部精神类疾病的诊断也能有很大的作用。

[1]Blinowska K，Muller-Putz G，Kaiser V，et a1.Multimodal imaging of human brain activity:rational，biophysical aspects and modes of integration[J].Comput.Intell.Neurosci.，2009：214-220.

[2]Jalili M，Knyazeva M G.Constructing brain functional networks from EEG:partial vs.unpartial correlations[J].Journal of Integrative Neuroscience，2011，10（2）:58-62.

[3]Boccaletti S，Latora V，Moreno Y，et al.Complex networks:Structure and dynamics[J].Phys.Rep.，2006（424）:175-308.

[4]Xiong H L，Zhang T X，Moon YS.A translation and scale invariant adaptive wavelet transform [J].IEEE Trans.on Image Processing，2000，9（12）:2100-2108.

[5]Richman JS，Moomaan JR.Physiologica time series analysis using approximate entropy and sample entropy[J].Am.J.Physio.Heart Circ.Physio.，2000（278）:H2039-H2049.

[6]Liu L，Qian X，Lu H， Cross-sample entropy of foreign exchange time series[J].Physica A，2010（389）:4785-4792.