改进的模糊Smith串级主汽温控制仿真研究

刘长良，张永波

(1.华北电力大学 新能源电力系统国家重点实验室，北京 100085;2.华北电力大学 控制与计算机工程学院，河北 保定 071003)

0 引言

火电厂锅炉过热蒸汽出口温度 (主汽温)是锅炉的重要参数之一，其对电厂的安全经济运行具有重要意义[1]。主汽温允许变化的范围一般为额定汽温的 +5～-10℃[2]，汽温过高或过低，以及大幅度的波动都将严重影响锅炉、汽轮机的安全和经济运行[3]，因此需要将主汽温控制在允许的范围之内。

火电厂的主汽温被控对象具有非线性，时变性和滞后性等特点，而且其动态特性易受环境的影响，难以确立精确的数学模型[4]，这使得常规的PID串级控制往往不能取得满意的控制性能[5]。在解决大惯性、大迟延问题方面，Smith预估是一种比较有效的控制方法[6]，但是它对被控对象的参数变化非常敏感，一般当过程参数变化10%～15%时，Smith预估补偿就失去了良好的控制效果[7]。C.C.Hang 提出的改进型 Smith 预估器[8]可以有效地改善传统Smith预估器的适应性。本文利用这种改进方法，结合模糊控制系统良好的不确定性、非线性的控制性能，提出了一种基于Smith预估的模糊PID主汽温控制系统。

1 主汽温控制系统结构

主汽温控制系统采用串级控制，通过改变减温水阀门开度来改变减温水量，从而调节主汽温度。由于常规PID温度控制器难以适应汽温控制系统的动态变化特性，常规Smith预估控制对于大时滞对象具有较好的控制效果，但是主汽温对象的时变性使得一般的Smith预估难以在实际应用中得到理想的控制效果。因此本文采用一种改进型Smith预估，同时为了提高控制系统的鲁棒性，主控制器采用模糊规则在线调整PID参数，从而消除模型参数变化对系统的影响。本文设计的串级控制系统结构如图1所示。

图1 模糊Smith串级系统结构Fig.1 The structure of fuzzy Smith cascade system

在串级控制系统中，内环对控制精度要求较低，用来迅速消除内环的扰动，故内环的副控制器C1(x)为PI控制器;主控制器采用模糊控制器，用来克服参数变化对系统的影响，G1(s)，G2(s)分别为导前区和惰性区的传递函数，H1(s)，H2(s)分别为导前汽温和主汽温的测量单元特性，r为主汽温的设定输入值，y为过热器出口温度实际值，d1，d2为系统扰动输入等效值，它们分别对应于减温水自发内扰和燃烧率变化等外扰。串级控制系统的外环主控制器采用模糊控制，并采用Smith预估器对整个系统的纯滞后进行补偿，来减小纯滞后系统的超调，增强系统的稳定性。

经推导可得出主控制器的广义被控对象Gp(s)为

为了在外环采用Smith预估，主控制器后的部分可等效为一个整体的被控对象，可将其等效为一阶纯滞后环节:

式中:Km，Tm，τm分别为对象参考模型的过程增益、时间常数和纯滞后时间。

2 基于Smith预估的模糊PID串级主汽温控制系统

2.1 改进的Smith预估控制

Smith预估控制的基本原理是通过被控对象的动态特性，利用预估模型进行补偿，使被控量超前反馈到控制器，使调节器提前动作，从而有效地改善大时滞控制系统的动态性能。Smith预估控制原理如图2所示。

图2 Smith预估控制原理Fig.2 The theory of Smith predictive control

图2中被控对象传递函数为Gp(s)e-τps，τ为时滞时间常数，Gm(s)为对象模型中不含时滞部分的传递函数，e-τms为对象模型时滞部分，当模型准确时，即 Gp(s)e-τps=Gm(s)e-τms时，经Smith预估补偿后的闭环传递函数为:

此时在系统的特征方程中已不包含e-τs项，说明系统已经消除了纯滞后对系统控制品质的影响，只是响应在时间坐标上向后推迟了一个e-τs时间。

但是，Smith预估控制存在着一个很大的缺点:非常依赖于精确的数学模型和对外部扰动十分敏感，鲁棒性较差，为此C.C.Hang提出了一种改进型Smith预估器，它比原方案多了一个调节器，其方框图如图3所示。

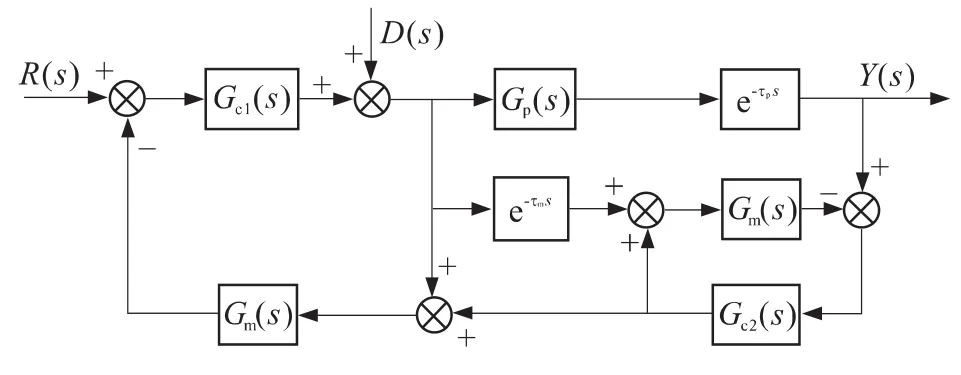
图3 改进型Smith预估控制Fig.3 Improved Smith predictor

改进型Smith预估多了一个调节器Gc2(s)，一般采用PI调节，它与Smith补偿器方案的区别在于主反馈回路，其反馈通道传递函数不是1，而是Gf(s)，即

由图可推导出此系统的传递函数为:

由上式可知，当Gp(s)=Gm(s)，τp=τm时，系统得到完全补偿，而当Gp(s)≠Gm(s)或τp≠τm时，只要Gc2(s)的PI参数选择的合适，系统能够克服过程动态参数变化的不利影响。辅助调节器Gc2(s)的整定似乎要复杂一些，但经分析发现，辅助调节器是在反馈通道上，且与模型传递函数Gm(s)一起构成了Gf(s)。如果假设Gm(s)是一阶环节，且设TI2=Tm，即，使调节器的积分时间等于模型的时间常数，则Gf(s)可以简化为

因此改进型Smith预估控制方案也可用图4表示。

图4 改进型Smith预估控制Fig.4 Improved Smith predictor

这样，反馈回路上出现了一个一阶滤波器[9]，使被控对象的输出和预估器的输出之间的偏差经过一阶惯性环节的滤波后才反馈到控制器，这就减缓了误差干扰系统的速度，削弱了模型不匹配对系统的影响，有利于系统稳定。此改进方法只有一个整定参数Tf，实质上只有Gc2(s)中的比例增益Kc2需要整定，它是比较容易在线调整的。文献[4]经过分析比较广义被控对象时间常数T0和纯滞后时间τ0变化时的ITAE积分综合指标，证明了时间常数T0和纯滞后时间τ0在较宽的范围变化时，这种改进型Smith预估控制仍有较强的适应性，对具有纯滞后的过程控制具有工业实用价值。

2.2 外环主控制器设计

主回路的控制对象为温度控制，容量滞后大，对超调量和静态误差要求都较高，故主控制器选用PID控制[10]，为提高系统对模型参数变化的适应能力，采用模糊规则对PID参数进行调整，模糊控制是以模糊集合论、模糊语言变量及模糊逻辑推理为基础的计算机智能控制，模糊控制具有较强的鲁棒性，对控制对象参数变化不敏感，有较强的抗干扰性，它不依赖于系统精确的数学模型，特别适合系统复杂且要求控制精确的系统中应用。本设计利用模糊规则，在PID初值基础上通过自调整参数，改善系统动态性能[11]。基于模糊控制的外环主控制器结构如图5所示。

图5 基于Smith预估的模糊PID控制器Fig.5 Fuzzy PID compound control system

本模糊控制器以偏差和偏差变化率的绝对值|e|和|ec|为输入语言变量，以 ΔKp，ΔKi，ΔKd为输出语言变量，以输入、输出的语言变量的语言值均为 4个:B(大)，M(中)，S(小)，ZO(零)，各模糊变量隶属函数均选用三角形，离散论域均为[0，1，2，3]。

利用模糊控制规则，可以比较容易地实现对PID控制器参数的在线调整，模糊控制设计的核心是总结技术知识和实际操作经验，建立合适的模糊规则表，得到针对3个参数ΔKp，ΔKi，ΔKd分别整定的模糊控制表。通过积累大量操作经验知道，ΔKp，ΔKi，ΔKd3个参数与输入控制器的偏差e、偏差变化率ec之间，存在着一种非线性关系。这些关系虽然无法用清晰的数学表达式描述，却可以用模糊语言表述。

在PID控制系统中，积分环节主要用于消除静差，提高系统的无差度，但是积分作用过强会造成系统超调增大，甚至引起振荡;比例环节用来加快系统的响应速度，提高调解精度，比例作用过大同样会引起系统不稳定;微分环节反应偏差信号的变化趋势，能在偏差信号值变得太大之前加入一个修正信号，加快系统的响应速度，减少超调时间，但它对干扰信号同样敏感，会使系统抑制干扰的能力下降。通过多次操作经验总结并结合理论分析可以归纳出偏差e、偏差变化率ec跟PID的 3个参数 ΔKp，ΔKi，ΔKd间存在如下关系:

(1)当|e(t)|较大时，为加快系统的响应速度，应取较大的Kp;为避免系统在开始时可能引起的超范围控制作用，应取较小的Kd;为避免出现较大的超调，应使Ki尽可能小。

(2)当|e(t)|处于中等大小时，应取较小的Kp，使系统的超调减小;此时Kd的取值对系统较为关键，为保证系统的响应速度，Kd要取值恰当;此时可适当增加一点Ki，但不得过大。

(3)当|e(t)|较小时，为使系统具有良好的稳态性能，可取较大的Kp和Ki;为避免系统在平衡点振荡，Kd的取值应恰当。

基于上述总结的输入变量e与Kp，Ki，Kd的定性关系，考虑偏差变化率ec的影响，可得模糊控制规则，如表1、表2、表3所示。

表1 Kp的模糊控制规则Tab.1 Fuzzy control rules of Kp

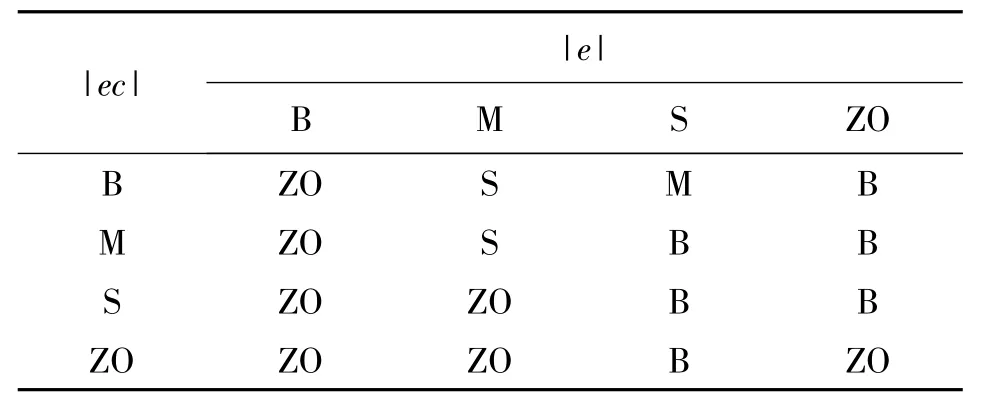
表2 Ki的模糊控制规则Tab.2 Fuzzy control rules of Ki

表3 Kd的模糊控制规则Tab.3 Fuzzy control rules of Kd

对输入的偏差e和偏差变化ec，取得相应的语言值后，根据模糊规则表，经过查表模糊决策，采用Mamdani模糊推理方法，分别得到3个修正值的模糊量，然后采用加权平均法求取输出量的精确值，再乘以比例因子，得出对原PID参数的修正值 ΔKp，ΔKi，ΔKd，系统实时的参数取值应该分别为 Kp+ΔKp，Ki+ΔKi，Kd+ΔKd。

3 控制系统仿真研究

设某锅炉在某种工况下，过热汽温对减温水量的动态特性为[12]

测量单元特性为

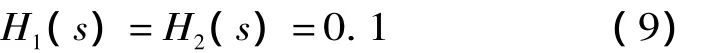
为检验所设计的控制系统的控制品质和鲁棒性，将本文设计的控制系统运用Matlab软件进行仿真分析，并与常规的串级PID串级控制系统进行仿真比较。

3.1 正常情况

对仿真模型施加单位阶跃信号，两种控制方法的响应曲线如图6。

图6 阶跃响应曲线Fig.6 Simulation result of step response

由图6可看出，与常规串级控制相比，采用Smith预估的模糊控制过渡过程短，超调量小，能够较好地解决大迟延问题。

3.2 加入扰动的情况

在常规串级控制和模糊Smith串级控制的内环加入一个减温水扰动信号 (d1=0.2)，该扰动信号在时间400 s时加入;在减温水扰动的基础上，在时间700 s时加入燃烧率变化扰动 (d2=0.2)，此时系统的输出曲线如图7。

图7 加入扰动时响应曲线Fig.7 Simulation curve of disturbance response

3.3 系统工况变化的情况

主汽温对象数学模型会随机组负荷的变化而变化，现场的许多原因也都会改变主汽温数学模型，如过热器管道的积灰结垢等，这就需要系统具有很强的鲁棒性，本文分别针对惰性区传递函数惯性增大和增益增大两种情况进行仿真。图8为惰性区惯性增大的响应曲线，Tm由25变为35，G2(s)=1.125/(35s+1)3。图 9为增益由1.125变为1.5的响应曲线，G(s)=1.5/(25s+1)3。

正常情况和模型参数变化时两种控制方法的性能指标如表4、表5、表6所示。

通过仿真曲线比较可看出，本文设计的基于改进的Smith预估模糊PID串级控制系统在正常工况、加入扰动及工况变化的情况下控制效果均优于常规的串级控制。特别是当工况发生改变时，新的串级控制系统在超调量、调节时间、衰减率等性能指标都比较理想，可见改进的Smith可以改善传统Smith预估对系统模型精度要求高的缺点，在模型参数发生变化时仍能保证一定的控制品质，从而提高系统的鲁棒性。

图8 惰性区惯性增大时响应曲线Fig.8 Simulation curve of gain increasing

图9 惰性区增益增大时响应曲线Fig.9 Simulation curve of inertia increasing

表4 正常情况时性能指标Tab.4 Performance of nomal condition

表5 惰性区惯性增大时性能指标Tab.5 Performance of gain increasing

表6 惰性区增益增大时性能指标Tab.6 Performance of inertia increasing

4 结论

本文针对电厂主汽温控制对象特点，在传统串级控制的基础上，运用Smith预估和模糊PID控制实现对主汽温的控制。改进的Smith预估器可以有效提高系统的适应能力和鲁棒性，从而更适用于工况不断变化的实际情况。主控制器运用模糊控制的原理实现对PID参数的修正，进一步提高了系统模型参数变化时的适应能力。通过仿真结果可以看出，这种方法对于电厂主汽温等缺乏精确数学模型和参数变化的大迟延工业过程具有较大的应用价值。

[1]黄宇，韩璞，李永玲.主汽温系统模糊自适应内模控制[J].中国电机工程学报，2008，28(23):93-98.Huang Yu，Han Pu，Li Yongling.Fuzzy adaptive internal model control in main steam temperature system[J].Proceedings of the CSEE，2008，28(23):93-98.

[2]李学明，刘吉臻，李志军，等.过热蒸汽温度控制系统优化[J].热力发电，2004，33(5):42-44.

[3]夏蕾，袁镇福.火电厂锅炉主汽温度控制策略研究[J].锅炉技术，2007，38(5):6-10.

[4]寇怀成，吴云洁，陈燕娥.基于模糊多模型的专家PID在主汽温控制系统中的应用研究[J].系统仿真学报，2008，20(23):6398-6400.Kou Huaicheng，Wu Yunjie，Cheng Yane.Study of expert PID main steam temperature control based on multiple models[J].Journal of System Simulation，2008，20(23):6398-6400.

[5]王鹏英.模糊Smith在温控系统中的仿真研究[J].计算机仿真，2011，28(6):247-250.Wang Pengying.Simulation on temperature control system based on fuzzy Smith[J].Computer Simulation，2011，28(6):247-250.

[6]张平，苑明哲，王宏.大时滞系统自适应模糊Smith控制[J].计算机仿真，2006，23(9):87-90.Zhang Ping，Yuan Mingzhe，Wang Hong.Self-adaptive fuzzy-Smith control for a long time-delay system[J].Computer Simulation，2006，23(9):87-90.

[7]崔晓波，王明春，张雨飞.一种改进的主汽温Smith预估补偿控制[J].锅炉技术，2011，42(4):23-26.

[8]金以慧.过程控制[M].清华大学出版社，1993:143-145.

[9]刘亭莉，黄廷磊.基于模糊Smith方法的温控系统仿真研究[J].计算机仿真，2010，27(2):170-174.Liu Tingli，Huang Tinglei.Simulation of temperature control system based on fuzzy Smith control[J].Computer Simulation，2010，27(2):170-174.

[10]张荷芳，王杰，易善伟.基于Smith预估的模糊PID串级中央空调水系统控制[J].西安工业大学学报，2012，32(4):330-333.

[11]黄宇，王东风，韩璞.模糊自整定PID控制及其在过热汽温系统中的应用[J].电力科学与工程，2004(3):37-40.

[12]陈来久.热工过程自动调节原理和应用[M].北京:水利电力出版社，1982:324-327.