一类混杂系统的模型辨识
2013-09-19赵丹丹谢春利王培昌
赵丹丹,谢春利,王培昌
(大连民族学院a.计算机科学与工程学院;b.机电信息工程学院;c.信息与通信工程学院,辽宁大连116605)
混杂系统是指在同一系统中同时包含连续动态部分与离散(逻辑)动态部分,以及它们之间相互影响,相互作用的一类系统。切换系统是混杂系统中极其重要的一种类型。该系统的连续动态由若干个子系统来描述,而离散动态决定某时刻系统的连续动态由哪个子系统来刻画,即子系统间是如何切换的。因此,离散动态通常称为切换律。输电系统、多控制器系统、服务器切换系统以及继电器系统等都是典型的切换系统,说明了切换系统具有广泛的实际工程背景。目前,国际控制界关于混杂系统的研究内容主要包括混杂系统的模型描述、性能分析、控制与优化和应用等。其中,关于混杂系统的建模方法受到了广泛的关注,并取得了大量的研究成果。主要的建模方法有代数几何方法[1]、混合整数规划方法[2],有界误差方法[3]、基于贝叶斯学习方法[4]以及基于聚类的方法[5]。尽管如此,切换系统的建模过程中,仍然面临许多问题,如降低计算的复杂度、对建模方法的优化和收敛性分析等。
考虑到切换系统与多模型系统具有相似性[6-7],因此,对样本数据聚类,采用多模型建模方法是解决这一问题的有效途径。文献[8]提出了基于条件正定核函数的核模糊C均值聚类算法,文献[9]提出了基于减法聚类的多模型辨识方法,文献[10]提出了基于粒子群优化的聚类算法。但这些聚类算法普遍存在聚类数据须事先给定,精度依赖数据分布和收敛速度慢等问题。多模型建模中常用的神经网络方法也存在过学习、局部极小等缺点,影响了模型的泛化能力。针对上述不足,本文提出一种基于仿射传播(AP)聚类的切换系统建模方法。利用AP聚类将样本数据聚类,对聚类后得到的子类进行最小二乘支持向量机建模,将各子模型组合形成最终切换系统模型。通过对一个切换系统的仿真研究,验证了所提出方法的有效性和可行性。
1 问题描述

本文考虑一类采用ARX形式描述的切换动态系统其中,xt为回归向量,即:xt=[ut-l-1…ut-l-nb,yt-1…yt-na,yt-1…yt-na],xt∈Rn,n=na+nbnu。nb,na为模型阶次;l为系统时延;,yt∈R,ut∈Rnu和 et∈R分别为系统的输出、输入和白噪声;λt∈{1,…,m}为离散的状态,即切换律;fλt为未知的线性或非线性光滑函数。
在假定切换系统模型结构已知的条件下(即:nb和na已知),则切换系统的模型辨识即为对fλt和λt的估计。
2 基于仿射传播聚类的切换系统建模
基于仿射传播聚类的切换系统建模算法如图1所示。首先采用仿射传播聚类对系统样本数据进行聚类,得到切换系统各连续子模型的数据样本,然后用最小二乘支持向量机对各连续子模型分别训练建模,得到各子模型。
2.1 仿射传播聚类算法
仿射传播聚类是一种新型的聚类算法[11],该算法无需预先给定聚类数目,聚类结果不会受初始聚类中心选择失当的影响,可快速有效地对大批量数据聚类。
AP聚类通过吸引度r(i,k)和归属度a(i,k)的计算,不断地从数据中选出合适的聚类中心。其中,r(i,k)表示数据点xk作为数据点xi聚类中心的适合度,a(i,k)表示数据点xi选择数据点xk作为聚类中心的适合度,r(i,k)和 a(i,k)越大,点xk成为最终聚类中心的可能性越大。s(i,k)表示任意样本点xi和xk之间的相似度。
依据文献[11]计算吸引度r和归属度a,有
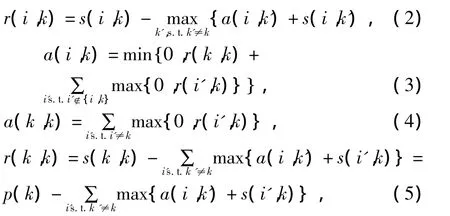
其中p偏向参数表示数据点xk被选作聚类中心的倾向性[12]。每一次循环迭代中,ri(i,k)和 ai(i,k)与前一迭代过程 ri-1(i,k)和 ai-1(i,k)加权更新,即
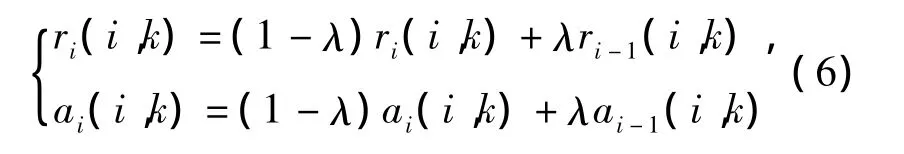
其中λ为阻尼因子。
对于数据点 xi使得{a(i,k)+r(i,k)}最大的数据点xk即为一个聚类中心。算法的收敛条件为聚类中心10次迭代不发生变化,或达到规定的最大迭代次数。迭代过程结束后,输出m个聚类中心及聚类。
2.2 最小二乘支持向量机
Suykens[13]提出的LS-SVM是通过将最小二乘线性系统引入支持向量机,代替传统的支持向量采用二次规划方法解决分类和函数估计问题。用于函数估计的LS-SVM算法推导如下:
设样本为n维向量,则N个样本组成的样本集表示为 D={(Xk,Yk)|k=1,2,…,N},X∈Rn,Yk∈R。其中:Xk为输入数据,Yk为输出数据。在权w空间中的函数估计问题描述如下:
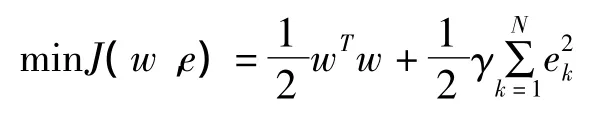
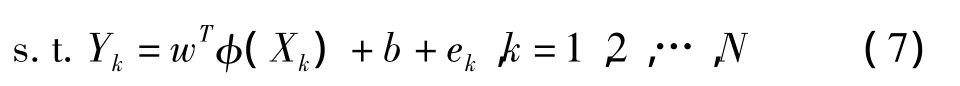
其中,φ(·):Rn→Rnh为核空间映射函数,w∈Rnh为权矢量,ek∈R为不敏感损失函数的松弛因子,b∈R为偏移量,γ∈R为正则化参数。根据式(7),可定义拉格朗日函数
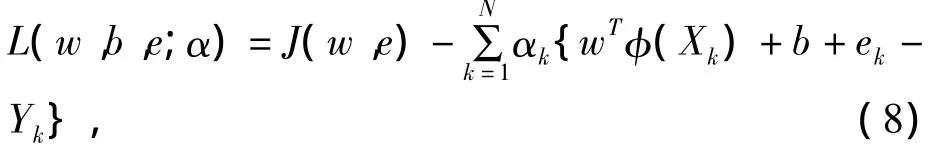
其中拉格朗日乘子αk∈R.通过L对w,b,ek和αk求偏导等于零,对式(8)进行优化,消除变量w和e,可得优化问题的解析解为

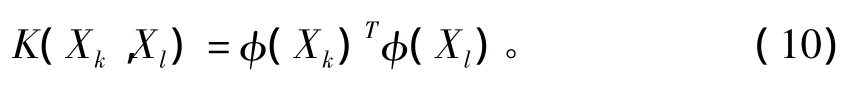
LS-SVM的函数估计为
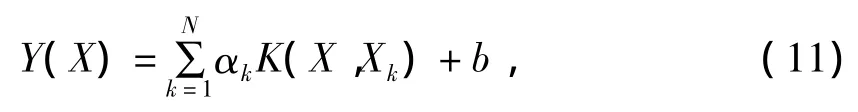
其中α和b由式(9)求解。
选择不同形式的核函数可以构建不同的支持向量机,较为常见的核函数有以下几种:
(1)线性核函数
K(Xi·X)=Xi·X
(2)多项式核函数
K(Xi·X)=(Xi·X+1)d
(3)高斯核函数
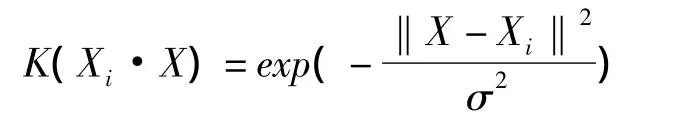
2.3 建模步骤
在n维空间定义两点之间的欧氏距离

则本文提出的基于仿射传播聚类和LS-SVM切换系统建模方法的具体步骤为:
步骤1 采用AP聚类算法将训练样本聚类。初始化AP聚类算法的p和λ,λ的值可以根据对象大小在0.5~0.9之间设置,偏向参数p取相似度矩阵的中值。
步骤2 根据各样本点和聚类中心的欧式距离确定各子模型的数据样本。
步骤3 各子模型采用LS-SVM训练建模并确定其模型参数。
3 仿真验证
考虑文献[14]中所描述的单输入单输出的切换系统
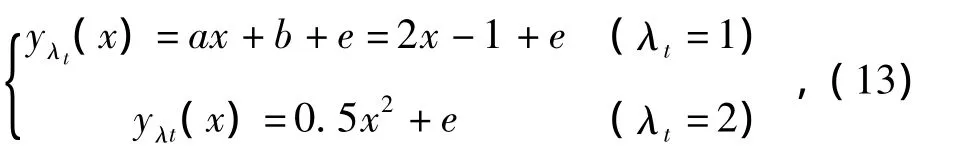
其中,e为均值0、标准差0.5的高斯噪声。离散状态λt与输入变量x无关,其值决定了系统的输出模型。令x在[-5,1]区间取值,对系统输出y1和y2分别采样30个数据。除了采样的这60对数据之外,只知道系统有一个模型是线性的,另一个模型是非线性的。仿真研究的目标就是能正确的对两个模型的数据进行分类,同时,对每个子模型进行建模。
用仿射传播聚类的方法训练样本聚类,采用欧式距离作为样本点之间的相似度测度,偏向参数p取为相似度矩阵中元素的中值,阻尼因子λ取0.5,通过聚类得到两子类数据。对两子类数据分别采用线性核函数和高斯核函数的最小二乘支持向量机建模,仿真结果曲线如图2。其中,线性核函数参数γ=200,高斯核函数参数γ=1 000,σ=3。线性子模型的参数估计为=2.0 098=-0.9 804,整个建模数据的均方误差为MSE=(其中为最小二乘支持向量机的估计值)。
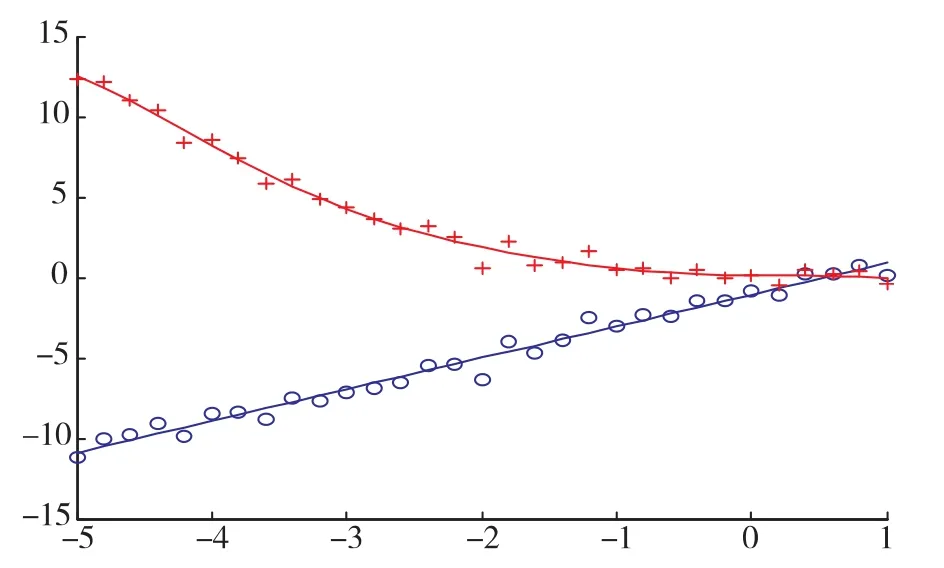
图2 切换系统建模曲线
4 结语
针对具有切换结构的混杂系统,本文提出一种基于仿射传播聚类和最小二乘支持向量机的辨识方法。该方法将切换系统看作是多模型的非线性系统,通过仿射传播聚类对系统的输出样本数据进行聚类,得到切换系统的各连续子模型的数据聚类中心,利用欧氏距离确定每个子模型的样本数据。基于最小二乘支持向量机对子模型进行建模。最后通过文献中的典型切换系统模型验证本算法的有效性。
[1] MA Y,VIDAL R.Identification of deterministic switched ARX systems via identification of algebraic varieties.In:Morari[J].M,2005,3414:449-465.
[2] ROLL J,BEMPORAD A,LJUNG L.Identification of piecewise affine systems via mixed-integer programming[J].Automatica,2004,40:37-50.
[3] BEMPORAD A,GARULLI A,PAOLETTI S,et al.A bounded-error approach to piecewise affine system identification[J].IEEE Trans.On Automatic Control,2005,50(10):1567-1580.
[4] JULOSKI A L,WEILAND S,HEEMELS W.A bayesian approach to identification of hybrid systems[J].IEEE Trans.on Automatic Control,2005,50(10):1520-1533.
[5] FERRARI-TRECATE G,MUSELLI M,LIBERARI D,et al.A clustering technique for the identification of piecewise affine systems[J].Automatica 2003,39:205-217.
[6] PETRIDIS V,KEHAGIAS A.Identification of switched dynamical systems using multiple models[C]∥Proceedings of the 37th IEEE Conference on Decision&Control Tampa,1998:199-204.
[7] VERRIEST E I,MOOR B D.Multi-mode system identification[Z].New York:In Proceedings of the European Control Conference(ECC'99),1999.
[8] 李卫,杨煜普,王娜.基于核模糊聚类的多模型LSSVM 回归建模[J].控制与决策,2008,23(5):560-562,566.
[9] 潘天红,薛振框,李少远.基于减法聚类的多模型在线辨[J].自动化学报,2009,35(2):220-224.
[10]徐海霞,刘国海,周大为,等.基于改进核模糊聚类算法的软测量建模研究[J].仪器仪表学报,2009,30(10):2226-2231.
[11]FREY B J,DUECK D.Clustering by passing message between data points[J].Science,2007,315(5814):972-976.
[12]王开军,张军英,李丹,等.自适应仿射传播聚类[J].自动化学报,2007,33(12):1242-1246.
[13]SUYKENS J K,VANDEWALLE J.Least squares support vector machine classifiers[J].Neural Network Letters,1999,9(3):293-300.
[14]FABIEN L,GÉRARD B.Switched and piecewise nonlinear hybrid system identification[C]∥HSCC'08 Proceedings of the 11th international workshop on Hybrid Systems:Computation and Control,2008:330-343.
