基于粒子群优化算法的室内定位方法
2013-09-19王小斌关维国慕文静
王小斌 关维国 程 猛 慕文静
(辽宁工业大学电子信息工程学院 辽宁 121001)
0 引言
定位技术是无线传感器网络的主要支撑技术之一。获取传感器节点的位置信息是传感器网络应用的一种重要组成部分,在室内进行无线传感器节点位置定位成为研究热点。
为了提高节点的定位精度,将粒子群优化算法引入到无线传感器网络定位中,通过迭代算法寻求最优解。
文献[1]将粒子群优化算法与质心定位算法相结合,定位效果好,但是过程比较复杂,定位精度没有明显的提高。
文献[2]把混沌寻优思想引入到粒子群优化算法中,在参数合理设置的前提下,算法性能稳定,并且具有较快的定位速度和较高的定位精度。
1 粒子群优化算法描述
1.1 粒子群优化算法的数学描述[3]
假设在一个 D维的空间中,有 N个代表存在问题解的粒子组成一个初始群体,其中,每一个粒子都可以表示为一个D维的向量:第 i个粒子在D维空间中的位置是 Xi,粒子更新速度令 Pi为第i个粒子目前为止搜索到的个体最优位置解所对应的位置坐标,令 Pg为粒子群目前为止搜索到的全局最优位置解所对应的位置坐标每次迭代中粒子按照式(1)、(2)更新速度与位置:
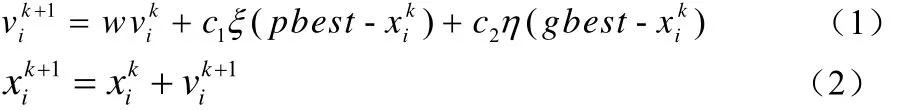
式中i= 1,2,3...,N ; k为迭代次数;w为惯性权重; c1,c2为学习因子;ξ,η是随机数。pbest为个体最优值;gbest为全局最优值。粒子通过不断的自身总结和学习更新,最后找的 Pg就是全局最优解。
1.2 粒子群优化算法参数[4][5]
参数一为常用的固定参数: w = 0 .6, c1 = c 2 = 1 .7。
参数二引入压缩因子的粒子群优化算法, w = 0 .6,c1 = c 2 = 1 .494。
1.3 适应度函数
适应度函数用来评价粒子群优化算法中各个粒子在种群中接近于最优解的优劣程度,从中选取每个粒子的个体最优解和种群的全局最优解。
适应度函数一:设为求未知节点估计位置到各个信标节点距离与测量距离差的方差最小值问题。

此函数值越小,得到的位置解越优。
适应度函数二:基于测距的定位算法中n个信标节点可得n个距离公式,进而可以线性化为 n -1维的矩阵方程Ax=B,由于实际中误差存在,设xAx+ N = B,N为 n -1维的误差向量,借用最小二乘法的原理, 的值应该是误差向量N = B - A x达到最小值的取值,即用最小化Q(x) = N2= B- A x2求x的估计,同时引用加权最小二乘法,引入N的协方差矩阵 cov(N),令适应度函数为(4)式:

2 仿真结果及分析
设节点的通信范围是在 20m×20m 的平面室内区域内,信标节点坐标分别为A(0,0),B(0,20),C(20,0),D(20,20)。未知节点坐标为E(13,9)。
粒子群的种群大小 40N= ,将总的迭代次数 100T= ,经MATLAB7.1进行仿真实验,为便于观察,适应度函数里距离id取值为未知节点E到信标节点真实距离,得图1为三种参数(2.2中)的适应度函数值收敛曲线对比图。

图1 收敛曲线对比图
由图1可知,选择参数一的情况下大约迭代50次逐渐趋于平稳;选择参数二的情况大约迭代30次;选择参数三大约迭代20次。
以下是适应度函数一与适应度函数二定位误差的比较,为尽量减少迭代次数,使用参数三,仿真结果如图2所示。
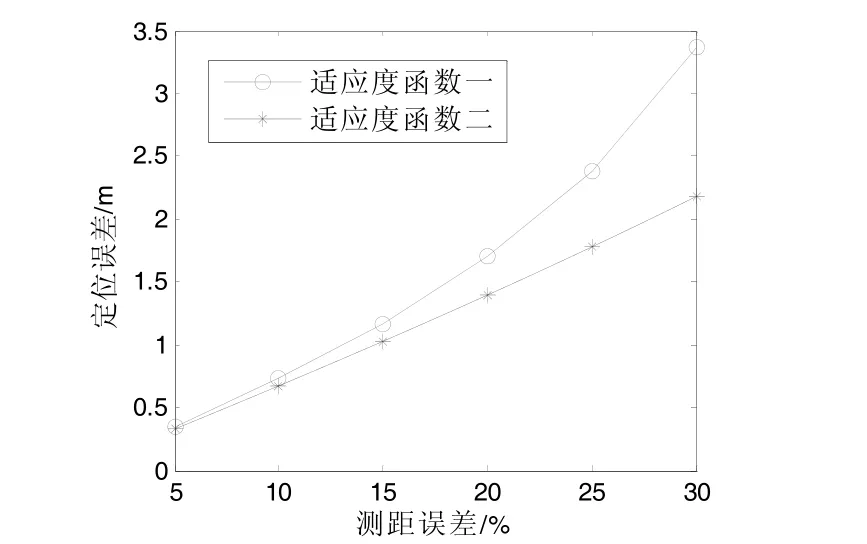
图2 定位误差图
适应度函数二比适应度函数一有更好的定位效果,这是因为应用粒子群优化算法,无论在测距误差较小还是较大情况下,都能通过多次迭代寻找最优解,从而减弱了测距误差引入的噪声影响。
3 结 论
与经典的粒子群滤波算法相比,本文通过修改参数,减少了迭代次数,降低了算法复杂度,应用新的适应度函数,与传统的适应度函数相比,新的适应度函数因为取误差公式的最小化估计,比单纯的优化误差的最小值更能得到精确的位置坐标,定位精度有明显提高。
[1]王新芳,张冰,冯友兵.基于粒子群优化的改进加权质心定位算法[J].网络与通信,2012,38(01):90-95.
[2]史洪宇,燕莎,曹建忠.无线传感器网络节点定位的混沌粒子群优化算法[J].探测与控制学报,2010,32(5):46-49.
[3]雷秀娟,史忠科.粒子群优化算法在函数优化中的应用及参数分析[J].计算机工程与应用.2008,44(28):53-55.
[4]王俊伟,汪定伟.粒子群算法中惯性权重的实验与分析[J].系统工程学报,2005,20(2):194-198.
[5]鲁雅静.基于粒子群优化算法的无线传感器网络节点定位技术研究[D].合肥:合肥工业大学,2012.
[6]王晓乐,徐家品.基于粒子群优化算法的WSN节点定位研究[J].计算机应用,2009,29(02):494-499.
[7]陈志奎,司威,传感器网络的粒子群优化定位算法[J].通信技术,2011,44(01):102-108.
