碱金属与碱土金属密堆积结构的研究
2013-09-18金冲洪玠巍张传杰熊世豪
金冲 洪玠巍 张传杰 熊世豪
(北京大学化学与分子工程学院2010级本科生 北京100871)
金属单质的结构随着压强和周期数的变化,常常呈现一定规律。常压下和高压下测定的金属结构给科学工作者带来了丰富的研究内容,而量子能带计算理论的发展提供了强有力的理论工具。图1为金属单质在低温下的晶体结构[1]。其中有一些显著的规律,如过渡金属的晶体结构,除了3d铁磁金属,3个周期均呈hcp→bcc→hcp→fcc的变化。对于镧系元素,则总体上呈hcp→dhcp→Sm型→hcp的变化规律。对于第三周期元素,在常温下,从Na、Mg、Al到Si,呈现bcc→hcp→fcc→金刚石型的变化[2]。对于这些规律,前人根据理论计算,证明d电子对于结构变化起主要作用[2]。本文通过理论计算和定性解释,讨论碱金属和碱土金属的结构及其变化规律。

图1 金属单质在低温下的晶体结构[1]
1 计算方法
本文使用的方法,基于线性化糕模轨道(LMTO)法[1]。对于多面体WS原胞(Wigner-Seitz cell)的球形中心区,糕模轨道法采用原子球轨道为基础波函数[3]。LMTO法的优点在于,同类型的基本函数可以适用于所有元素,从而能对元素周期表中晶体结构变化趋势给出有效解释,而且在计算机上特别高效。由于我们主要关心的是变化趋势,忽略了对电荷密度的非球体对称贡献,而该项忽略是导致计算能量差值偏大的系统误差。同时,我们忽略了在原子球之间的一项与结构有关的静电作用,除了少数对于能量差起到明显作用的情况。
我们使用LMTO方法中的原子球近似(ASA,atomic sphere approximation)和对于ASA的修正。同时我们考虑了相对论效应,但忽略自旋-轨道耦合,采用von Barth和Hedin给出的交换关联项,以及冻芯近似(frozen potential approximation)。
2 基于计算结果的分析
通过对于LMTO-ASA方法的计算结果的分析,我们可以对碱金属和碱土金属的结构进行解释。
2.1 碱金属
经过计算,在平衡态下,碱金属各个结构的能量差值几乎比其他金属(例如碱土金属)小2个数量级。为了判断这种计算方法的精确性,Skriver研究了以压力为自变量的不同结构的能量差异。图2表示出了从平衡态到压缩至2.5的压缩比;图2中的结果包含了对Madelung常数的修正。

图2 碱金属在低温下的结构能量差-压强(比体积)计算值曲线
图2 下方的横坐标是V/V0,上方的横坐标则是与压缩体积相对应的压强;纵坐标表示以fcc结构为零点,bcc结构和hcp结构的能量差值。从图2可以看出,遵循能量最低原则,相对较重的碱金属在低温和低压下应当是bcc结构,而Li应当是 hcp结构;但从实验测定可得,在常温下所有5种碱金属都是bcc结构[4],并且除了Na在温度低于51K时会转变成hcp的结构,以及Li在低温时会同时出现hcp和fcc两种结构,其余金属在温度下降至5K时依然保持这一结构。因此,除了Na之外,低压下碱金属的密堆积结构都被正确地预测了。见表1。
由于图2仅包含了对3种晶体结构的计算,所以错误地计算了Cs在压缩系数为2.2时会转换成bcc结构。然而在一项涉及s-d跃迁对Cs的研究中,McMahan[5]指出,在bcc比fcc变得更为稳定之前,Cs已经转化成了Cs IV的结构,这与高压实验的结果相符[6-7]。
碱金属各种结构之间的结构能量差非常微小,这是使计算所得的结构与实际结构有所差别的重要原因,也是Na的结构无法正确预测的原因。

表1 碱金属在不同条件下和计算预测的稳定结构
2.2 碱土金属
2.2.1 碱土金属常温下的晶体结构稳定性
图3为计算所得在不同压力下碱土金属的各种结构的能量差。在图3中,金属以它们计算所得的平衡时d电子占有数来排序。在常压下Be和Mg的结果在图4中显示。

图3 碱土金属在低温下的结构相对能量-压强(压缩体积比)曲线
图3 显示了各个碱土金属及两个稀土金属(价电子排布与碱土金属相似)结构能量差对压强的函数关系,计算中包含了s,p,d轨道,但是没有包含Madelung常数的修正。
根据图3和图4,Be、Mg在低温下应当是hcp结构,Ca、Sr在低温低压下应当是fcc结构,而Ba应当是bcc结构。这些预测都与实验相符[4]。
2.2.2 碱土金属压强不同情况时的结构转变
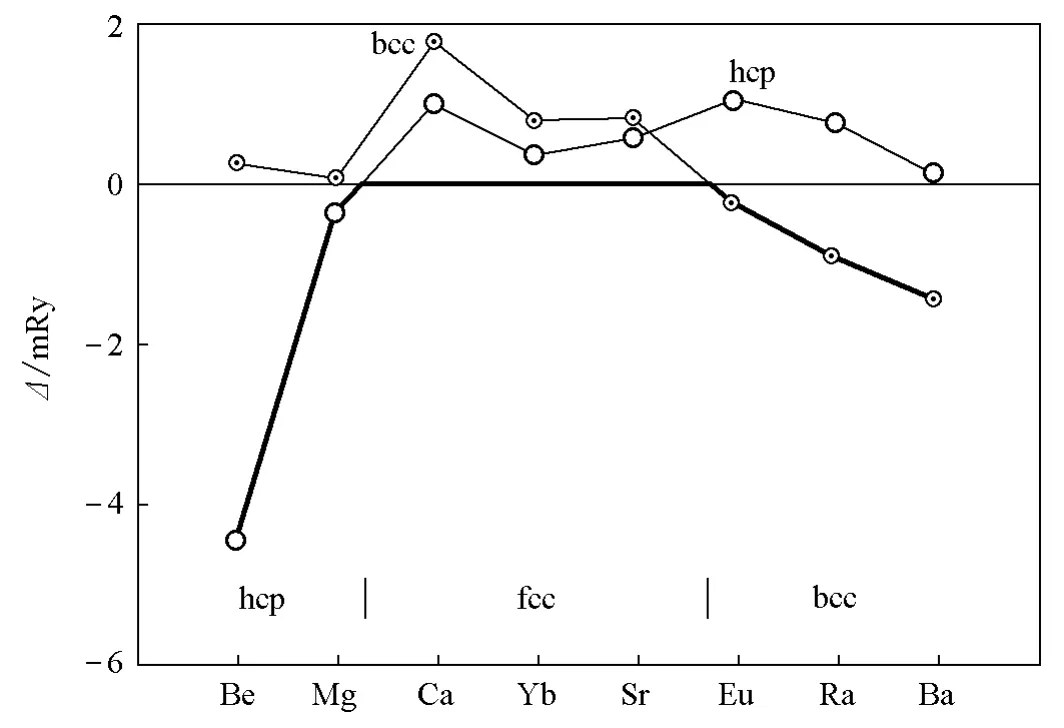
图4 碱土金属在常温常压下的不同结构相对能量计算值

图5 碱金属和碱土金属稳定结构随d占有数和压强的转变(计算值)
计算得到的d轨道的占有数和晶体结构有很强的相关性。从图5可以看出,重碱土金属同属于相同的“hcp→fcc→bcc→hcp”变化序列。在0压强下,每种碱土金属都处于连续的s-d电子跃迁的不同阶段,即d占有数不同。这是由于d能带的能量受到压强的影响,相对于s能带的能量下降。不同结构之间的相转变亦受此影响。然而,这种联系并不是完美的,计算所得的晶体结构的转变也仅仅在一个很小的d占有数范围内发生。
通过实验[8-11],在上述序列中的fcc→bcc的转变都已经被观测到。但是从bcc→hcp的转换仅在Ba中观测到。这是因为更轻的碱土金属转换成了更为复杂的高压相态[8],对此不予讨论。Ca、Sr发生fcc→bcc转变的临界压强经计算分别为21GPa和3.8GPa。而 Ba的 bcc→hcp转变压强则为10GPa。Olijnyk和 Holzapfel发现Ca在室温下发生相转变的实验压强为19.7GPa[8],而Jayaraman通过高压晶体学测量的低温外推法,给出了Sr发生相变的转变压强为4GPa[9-11],而Ba的bcc→hcp转变压强为5GPa。表2中整理并列出了相应的数据。考虑到图5并没有使用任何可调整的参数,计算所得的临界压强可以认为是令人满意的。
又由图5可见,在0压强下,不同碱金属之间d占有数相近,最大差值约为0.1;相比之下,不同碱土金属的d占有数差别较大,例如Ca和Ba的d占有数差值达到0.3。这可以从一个侧面解释不同碱金属结构相近,而不同碱土金属间结构存在显著差异的事实。

表2 Ca、Sr、Ba计算临界压强和实际转变压强的对比
2.3 从化学硬度的角度定性解释结构变化规律
由图5可知,增加压强和增大周期数,碱土金属稳定结构的变化规律是一致的。同周期轻元素高压下相态的结构和重元素常压下相态的结构常常相似[6]。Prewitt和Downs建立了高压下结构转变的一系列首要规则[7],其中第9条是:“高压下元素性质类似元素周期表中它下面的元素在低压下的情况”。因此,通过较轻的碱土金属随压强增大稳定结构的转变,可以推测出常压下重碱土金属变化的趋势。如何定性解释这一规律呢?化合物通常采取一种倾向于使整个体系化学硬度最大的原子核排列。化学硬度η=(Ea-χ)/2,其中Ea为电离能,χ为电子亲和能,硬度与满带和空带间一半的能量差大致对应。当压强超过100GPa时,一些在常压下能量相当高的激发态和体系的基态间会有更强的作用。能级扩展为能带,结果,满带和空带间的能量差常常消失。相应的激发态在高压下能量下降,致使与基态间的混杂程度上升[12],这是杂化的一种机理。第二周期元素通常较硬,压缩降低了激发态能量,使这些原子更软,允许重新杂化。结果,硬的、变形性低的原子表现出类似更重的原子的性质,变得更软,电子密度分布更加多变,方向性降低。因此,上述经验规律成立。从表3可以看出,随着化学硬度的下降,结构呈hcp→fcc→bcc的变化。

表3 碱土金属和碱金属的电离势、亲和势及化学硬度
3 总结
碱金属及碱土金属的结构计算基于量子能带计算理论。本文主要介绍了建立在密度泛函理论(DFT)和局域密度近似方法(LDA)之上的广义赝势理论(GPT)以及线性化糕模轨道法(LMTO),并使用了采取原子球近似(ASA)的LMTO法,计算并比较了碱金属及碱土金属在不同压力下的fcc、hcp、bcc 3种结构的能量差值。遵循能量最低原理,较成功地预测了常温下碱金属及碱土金属的晶体结构。对于碱土金属,还考虑了d轨道占有数对于晶体结构以及在不同压强下各种结构之间发生转变的关系,计算所得的临界压强和实际测定的转变压强也有很好的吻合。最后,使用Prewitt和Downs在高压下结构转变下的定性法则,对上述的理论计算进行了佐证与补充。
由于碱金属仅有一个s价电子,而碱土金属有2个s价电子。故两者的d轨道占有数会有较大的差别。所以碱金属不同结构之间的差异很小,而碱土金属的差别则较大。这也就可以解释为什么碱金属在常温下都是bcc结构,而碱土金属却存在着hcp→fcc→bcc这一变化序列。
[1]Skriver H L.Phys Rev B,1985,31:1909
[2]MacMahan A K,Moriarty JA.Phys Rev B,1983,27:3235
[3]http://home.educities.edu.tw/listeve/Htm/physics/phys-field-computing.htm
[4]Donohue J.The Structures of the Elements.New York:Wiley,1975
[5]McMahan A K.Phys Rev B,1984,29:5982
[6]Takemura K,MinoMura S,Shimomura O.Physics of Solids under High Pressure.Amsterdam:North-Holland,1981
[7]Takemura K,MinoMura S,Shimomura O.Phys Rev Lett,1982,49:1772
[8]Olijnyk H,Holzapfel W B.Phys Lett,1984,100A:191
[9]Jayaraman A,Jr Klement N,Kennedy G C.Phys Rev,1963,132:1620
[10]Jayaraman A.Phys Rev,1964,135A:1056
[11]Jayaraman A,Jr Klement W,Kennedy G C.Phys Rev Lett,1963,10:387
[12]MacMahan A K.Phys Rev B,1984,29:5982
