基于多水平系统的锥束ART算法

乔佳亮，王明泉，韩得水

（中北大学a.动态测试技术重点实验室;b.中北大学信息与通信工程学院，山西太原 030051）

基于多水平系统的锥束ART算法

乔佳亮a，b，王明泉a，b，韩得水a，b

（中北大学a.动态测试技术重点实验室;b.中北大学信息与通信工程学院，山西太原 030051）

代数重建技术（ART）是X－射线CT图像重建的一种重要迭代算法，投影的访问顺序对其收敛速度有重要影响。1994年，Guan和Gordon提出了多水平访问系统（MLS），该系统在投影数为2的整数次幂时效果最好。针对MLS仅适用于［0，π）上的均匀投影的问题，将MLS推广到［0，2π）上，在特定的投影数情形下，分析投影数特点，提出了三等分方法，该方法对对称投影访问顺序进行了改进。仿真实验结果表明，推广后的两系统下的锥束ART算法在迭代中收敛速度都要快于随机访问系统（RAS）和顺序访问系统（SAS）下的锥束ART算法。

锥束ART算法;CT图像重建;多水平访问系统;投影

ART算法是计算机断层成像技术（CT）中用于图像重建的一种重要方法，因其具有采用不完全投影数据也能实现较高成像质量的优点，在大型工业检测和地质勘探中应用广泛［1］。ART 主要缺点是计算量大，重建速度慢［2］。对此，很多学者从投影访问顺序、松弛因子的选择和并行计算等方面改进ART算法，提高迭代速度［3］。对于ART算法中的投影访问顺序系统，常用的有随机访问系统（RAS）［4］、多水平访问系统 （MLS）［5］等。

针对MLS仅适用于［0，π）上的均匀投影的问题，本文将MLS推广到［π，2π）上，首先将其在［0，π）上的顺序对称地应用在［π，2π）上，获得［π，2π）上的投影访问顺序，鉴于MLS在投影数为2的整数次幂时效果最好，在360个投影角度数情形下，本文采用三等分法对对称投影访问顺序进行了改进。仿真实验结果表明，改进后的投影访问顺序锥束ART算法在迭代中收敛速度要快于随机访问系统（RAS）和顺序访问系统（SAS）下的锥束ART算法。

1 多水平系统介绍

多水平系统（MLS）是一种较好的投影访问顺序系统，当投影方向数为2的幂次方时，系统具有很好的效果［6］。设投影方向总数为2的整数次幂，首先被访问的是第一层的数据，即投影在0（0°）和M/2（90°）方向最大程度正交。第三个被访问的是第二层的数据，此时投影角为M/4（45°），然后是3M/4（135°）。以此类推，接下来被访问的投影角分别为:M/8，5M/8，3M/8，7M/8等。表1给出了L=4时各层的访问顺序。

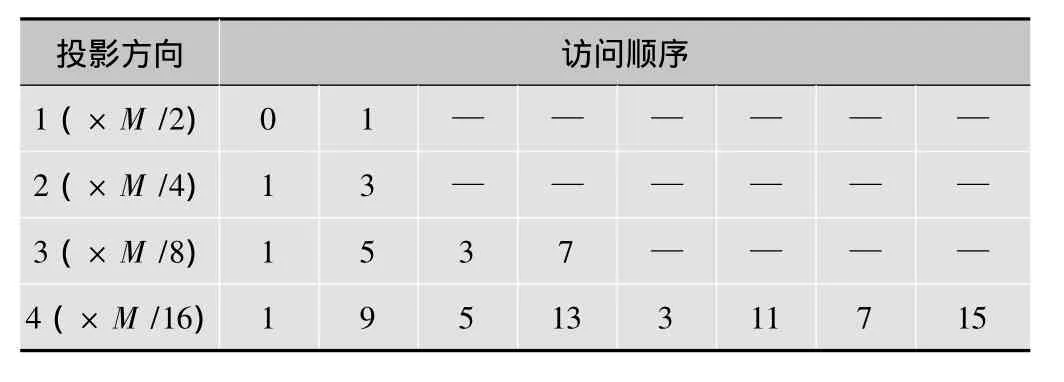
表1 MLS中M个投影方向的访问顺序

当投影方向总数不是2的整数次幂，即M≠2L时，也可以使用MLS顺序。在第一层时，可选任意两个成90°（或接近的）夹角的投影角度，在第二层时选取上述两个方向夹角的角平分线位置（或接近的位置），依次类推获得相应的投影角度。投影角度的访问顺序继续依据表1，总层数为L=［lbM］+1（［］表示取整）［7］。

2 ［0，2π）的多水平系统的ART算法

2.1 对称推广

考虑投影射线的相关性，在［0，π）上MLS是一个效果很好的投影顺序访问系统。将［0，π）上的MLS推广到［0，2π），可以将［0，π）上的 MLS 访问顺序中心对称用在［π，2π）上，该顺序系统在［0，π）和［π，2π）上分别达到了MLS的效果，本文称此系统为MLS1。设投影总数为2的整数次幂。表2列出了L=5时MLS1各层的访问顺序。图1给出了在［0，2π）上均匀分布的16个投影角度的MLS1访问顺序示意图。当投影总数不是2的整数次幂时，处理方法与［0，π）上MLS的处理方法相同。

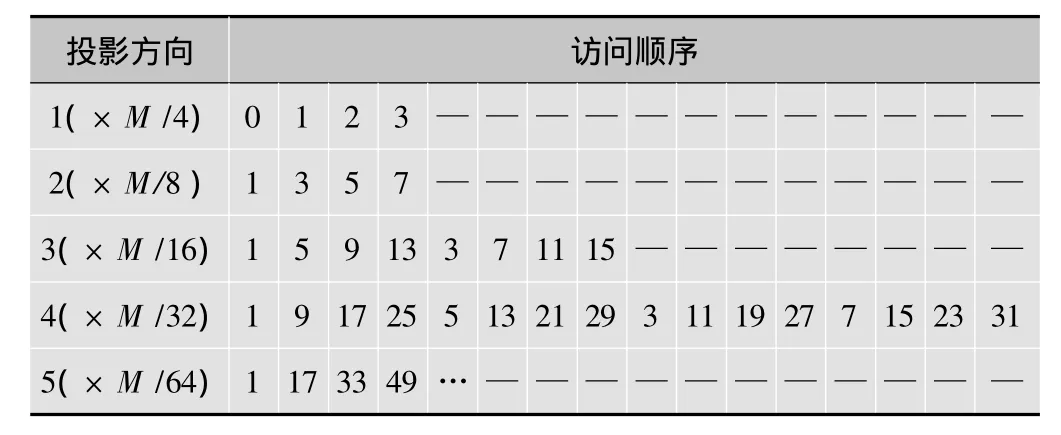
表2 MLS1下M个投影的访问顺序

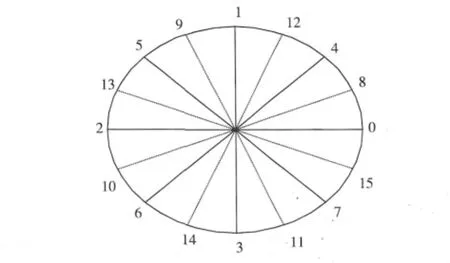
图1 在［0，2π）上均匀分布的16个投影角度的MLS1访问顺序

2.2 改进算法

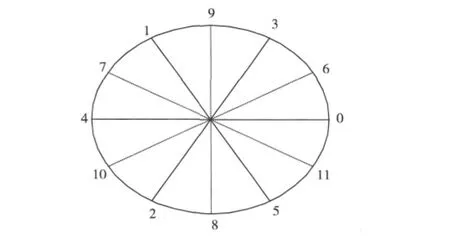
图2 在［0，2π）上均匀分布的12个投影角度的MLS2访问顺序

3 实验结果

将MLS1，MLS2，RAS，SAS应用到三维物体重建。在实验中，选用三维的Shepp－Logan模型，大小为128×128×128，设置参数为物距650，相距350，λ=0.2，投影射线数目为360×300×300，其中360为投影角度数，每隔1°取一次投影，300×300为探测器大小。

图3给出了4个系统下锥束ART算法一次迭代重建所得物体分别在x=0，y=0，z=0处的截面图，其中第1列为x=0截面图，第2列为y=0的截面图，第3列为z=0的截面图。与［0，π）上的重建一样，RAS的迭代中每次所用的随机数组都是不同的。

可以明显看出，推广后的MLS1和MLS2的效果优于SAS，为了更清楚地显示出MLS1，MLS2与RAS之间的差异，表3、表4分别给出了4种系统下重建的归一化均方距离d1、平均均方误差d3随迭代次数k的变化。

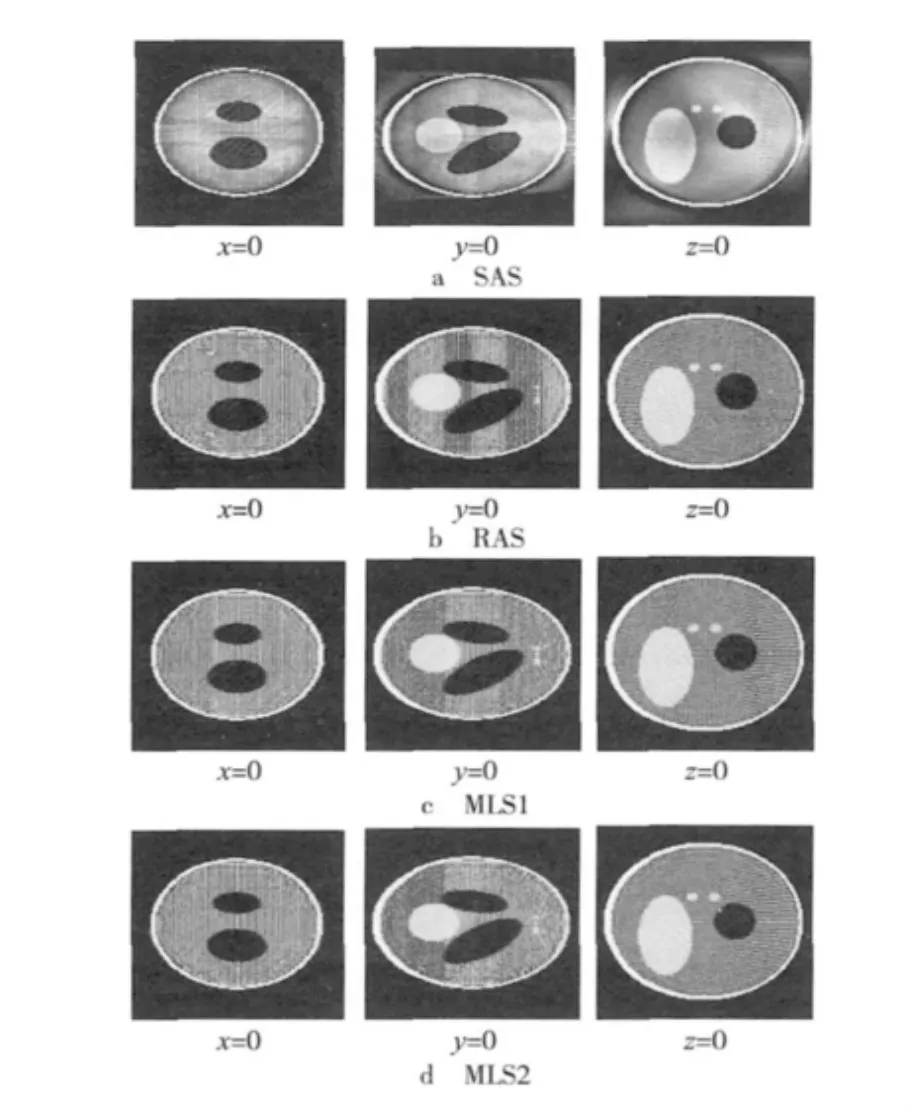
图3 SAS，RAS，MLS1，MLS2 的 ART 算法一次迭代所得物体的截面图

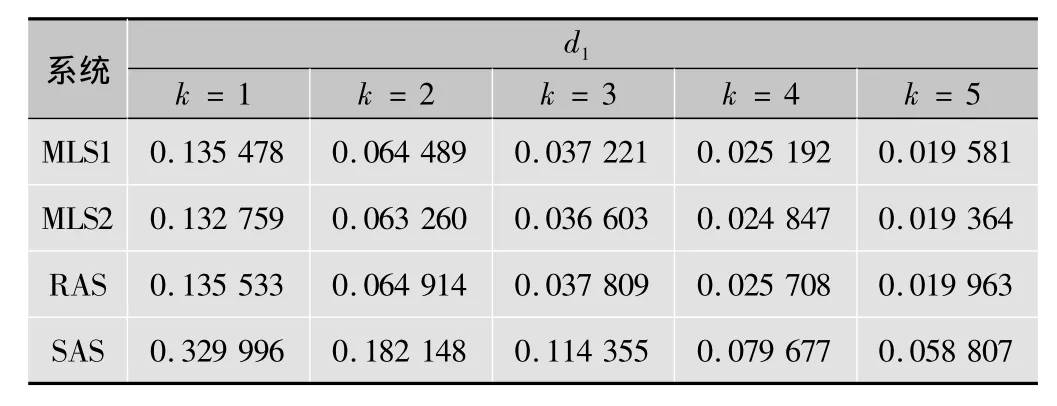
表3 4种系统下重建的归一化均方距离d1

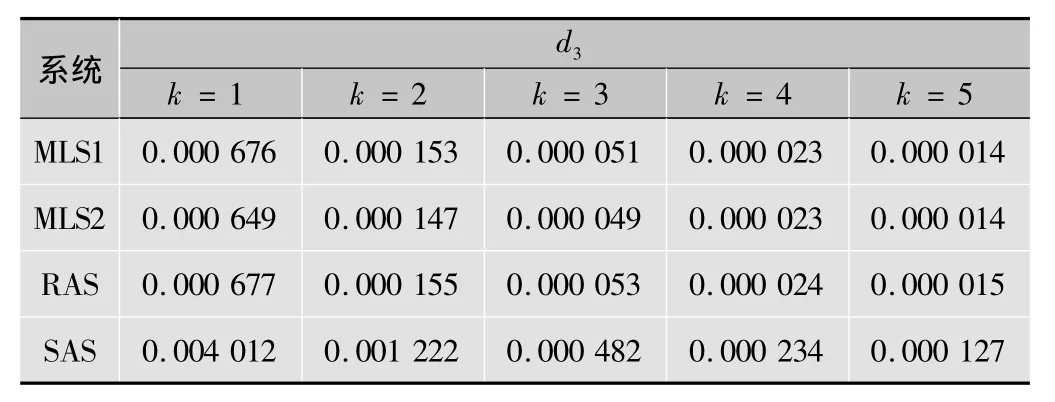
表4 4种系统下重建的平均均方误差d3

表3、表4表明，在前5次的迭代中，MLS2优于MLS1，MLS1优于RAS，3个系统都优于SAS。

4 结论

本文介绍了基于MLS的ART算法，并验证了其在三维锥束ART算法中相对于RAS和SAS的优越性。同时针对MLS仅适用于［0，π）上的均匀投影的问题，本文将MLS推广到0，2[）π上，在特定的投影数情形下，分析投影数特点，提出了三等分方法，该方法对对称投影访问顺序进行了改进。从实验结果可以看出，无论是基于何种情况，文中的方法都优于RAS和SAS，而且该方法在采用不完全投影数据的情况下也能成像出质量较高的图像，进一步验证了该方法确实是一种有效的图像重建算法。

:

［1］干宗良，粱秀聚.自适应稀疏约束图像超分辨力重建方法［J］.电视技术，2012，36（14）:19－23.

［2］周斌，王连堂，王俊杰，等.代数重建算法中一种快速投影系数计算方法［J］.计算机工程与应用，2008，44（25）:46－47.

［3］张顺利，张定华，王凯，等.一种基于ART算法的快速图像重建技术［J］.核电子学与探测技术，2007，27（3）:479－483.

［4］王宏钧，路宏年，傅健.代数重建技术中投影序列选择次序的研究［J］.光学技术，2006，32（3）:389－391.

［5］VAN D M C.Iterative methods in image reconstruction［D］.Netherlands:Utrecht University，1992.

［6］张顺利，张定华，赵歆波，等.工业CT图像重建的ART算法研究［J］.无损检测，2007，29（8）:453－456.

［7］孙开一.计算机模拟断层扫描技术［J］.科技资讯，2008（4）:103－104.

Multilevel Scheme for Cone－beam ART Algorithm

QIAO Jialianga，b，WANG Mingquana，b，HAN Deshuia，b

（a.Dynamic Testing Technology Key Laboratories，North University of China;b.School of Information and Communication Engineering，North University of China，Taiyuan 030051，China）

ART is one important iterative algorithm of CT image reconstruction using X－ray，while the sequential access of the projection is very important to the convergence rate.In 1994，Guan and Gordon raised multilevel scheme（MLS）which is best performance when the projection number is power of two.According to MLS only applies for the circumstance when projection is uniform in［0，π），then extend it to［0，2π）.Analyzing the features of the projection number in the certain projection number，the trisection method is proposed in this paper.This method is to promote the first method with trisection.The results of experiments show that convergence rate of cone－beam ART algorithms with the above two systems perform better than that with the RAS and SAS.

cone－beam ART algorithm;CT image reconstruction;MLS;projection

TN911.73

A

【本文献信息】乔佳亮，王明泉，韩得水.基于多水平系统的锥束ART算法［J］.电视技术，2013，37（13）.

国家自然科学基金项目（6171177）;山西省工业攻关项目基金项目（20110321073）;中北大学2011青年基金项目（201261413752398）

乔佳亮（1988— ），硕士生，研究方向为信号与信息处理;

王明泉（1970— ），博士生导师，研究方向为信息获取与处理技术、图像处理与识别;

韩得水（1989— ），硕士生，研究方向为信号与信息处理。

责任编辑:时 雯

2012－10－23