基于灰色马尔可夫修正模型的城市月用电需求预测

乔松珊，张建军

（1.中原工学院 信息商务学院，郑州 450007；2.河南农业大学 信息与管理科学学院，郑州 450002）

基于灰色马尔可夫修正模型的城市月用电需求预测

乔松珊1，张建军2

（1.中原工学院 信息商务学院，郑州 450007；2.河南农业大学 信息与管理科学学院，郑州 450002）

传统的灰色预测模型只能反映月用电量的总体变化趋势，不能反映月用电量随季节的波动特征。为此，基于马尔可夫理论提出了灰色马尔可夫修正预测模型，引入了马尔可夫修正系数，并在模型中加入等维信息，研究了同时考虑2种趋势的城市月用电需求的预测问题。算例表明，与传统的灰色预测方法相比，马尔可夫修正模型较好地提高了预测的精度。

月用电需求;灰色理论;马尔可夫理论;预测精度

用电需求预测是电力系统规划和运行研究的重要内容，科学的电力负荷预测结果是供电部门合理安排运行计划、降低运行成本的重要保障，也是提高供电可靠性的重要手段。电力负荷的预测有多种方法，灰色预测模型具有要求样本数据少、预测精度高、预测结果可检验性强等优点，因而在电力预测中得到广泛应用[1—4]。然而，对于随机性、波动性较大的数据，由于受到一些扰动因素影响，随着时间推移，数据拟合较差，导致月用电负荷预测精度变低。针对这一问题，本文对影响电力负荷的诸多因素进行分析，充分考虑月用电需求随季节波动的变化特征，将马尔可夫理论与灰色预测方法相结合，得到了灰色马尔可夫修正预测模型，该模型既可以反映时间序列的变动趋势，又可以反映月用电需求的波动特征，并应用该模型给出了郑州市月用电需求的预测方法，通过2种模型预测结果的对比，进一步说明了该模型的优良性。

1 灰色预测模型

GM（1,1）模型实质是对原始数据做一次累加生成，使生成的数据序列呈一定的规律，通过建立一阶微分方程模型，进而得到拟合曲线方程

对此作累减还原，得到原始序列的预测模型为

具体建模过程详见文献[5]。

2 灰色马尔可夫修正模型的构建

2.1 状态划分

2.2 构造状态转移矩阵

2.3 引入马尔可夫修正系数

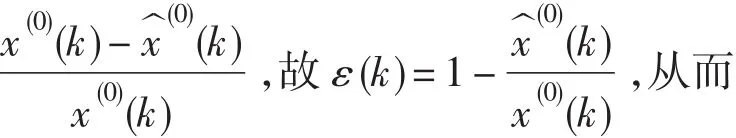
2.4 加入等维信息

传统GM（1，1）模型在建模时，采用的是k=n为止的过去的数据。然而，任何一个灰色系统的发展过程中，随着时间的推移，将会不断地有一些随机扰动因素进入系统，使系统的发展受到影响。因此，用传统GM（1，1）模型预测，精度较高的仅仅是最近的几个数据，越往未来发展，其预测意义就越小。为了反映未来的随机扰动对灰色系统的影响，提高预测精度，在使用灰色马尔可夫模型的同时不断加入新的数据。其过程为：

3 郑州市月用电需求模型的建立及结果分析

3.1 构建灰色马尔可夫模型

根据上述建模思想，以2010—2011年郑州市每月的社会用电量为历史数据（见表1），建立GM（1,1）及灰色马尔可夫模型。

首先，以2010—2011年24个月的月用电量为原始序列，建立灰色预测模型，得到

按照式（2）累减，得到原始数据的预测值

根据马尔可夫链状态划分标准和灰色预测值的相对误差实际分布情况，将系统划分为4个状态区间，详见表2。

不妨设灰色预测值处于第i个状态，则灰色马尔可夫模型预测值可取以下数值

表1 郑州市2010—2011年各月份用电量 亿kWh

表2 状态划分标准

由公式(4)、公式(5)求出原始序列的灰色预测值、马尔可夫状态、灰色马尔可夫预测值以及2种预测值的相对误差，具体计算结果见表3。

表3 2种模型对月用电需求的预测结果比较

3.2 确定马尔可夫修正系数和状态转移矩阵

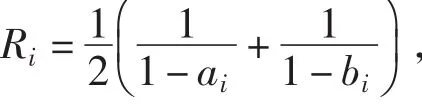
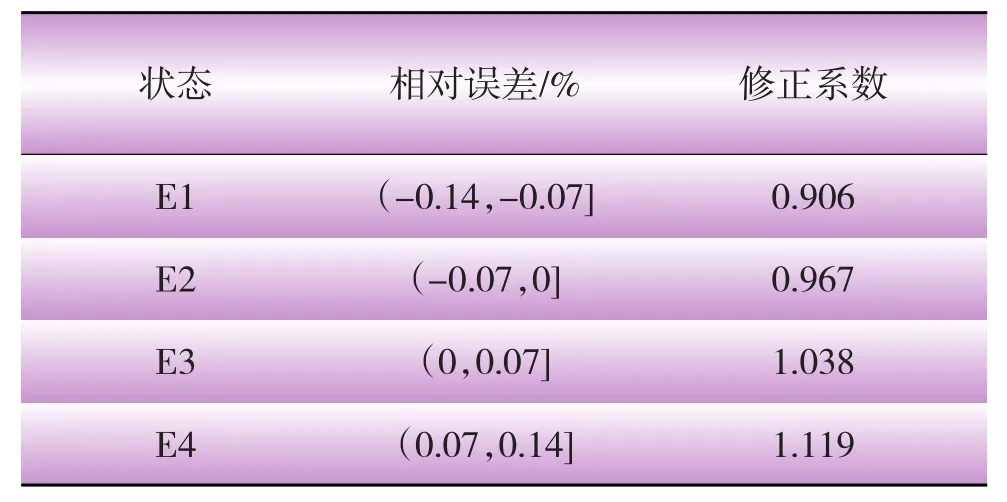
表4 马尔可夫修正系数

由于原始数据序列最后一个状态的转向不确定，所以去除2011年12月用电量，通过分析可知道一步转移矩阵为

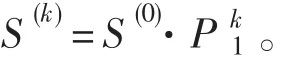
3.3 灰色马尔可夫修正模型检验

利用初始向量和状态转移矩阵，可以预测时间序列未来所处状态。例如：设2012年1月份系统状态为S(1)，则

去掉2010年1月用电数据，增加2012年1月修正值41.2，以这24个数据构造一组新的时间序列x′(0)=(29.5,34.6,…,41.2)，建立灰色模型，得到

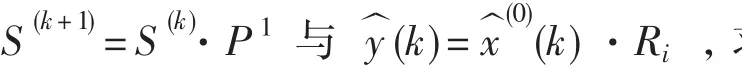
表5 2种方法对2012年1—5月用电需求预测结果比较 亿kWh

通过与实际用电需求比较，可以看出修正后的预测效果得到了很大的改善。平均相对误差由原来的0.055 66降低为0.020 16。由此可见，基于马尔可夫理论的修正灰色预测方法较好提高了预测精度，适合城市月度用电需求的预测问题。图1显示出了这2种方法分别对原始数据拟合的态势。

图1 2种方法对郑州市月用电需求预测的拟合态势

4 结束语

郑州市月度用电量具有明显的增长性和波动性特征，本文根据这一特点，基于马尔可夫理论对传统灰色预测模型改进，用平行于预测曲线的曲线将数据序列分成若干状态区间，并求出预测数据的修正系数。研究结果表明，该方法具有较高的精度，适合城市月度电力需求的预测问题，对城市用电需求的预测结果可为供电部门合理安排运行计划、低运行成本提供有力的帮助，具有很好的实用性。

：

[1]牛东晓,贾建荣.改进GM(1,1)模型在电力负荷预测中的应用[J].电力科学与工程,2008,24(4)：28-30.

[2]杜莉,张建军.神经网络在电力负荷预测中的应用[J].计算机仿真,2011,28(10)：297-300.

[3]李俊峰.GM(1,1)改进模型的研究及在上海市发电量建模中的应用[J].系统工程理论与实践,2005,25(3)：140-144.

[4]范鹰，郭建伟.灰色模型在电力负荷预测中的应用与改进[J].电力需求侧管理,2006,(3)：18-25．

[5]刘思峰，党耀国,方志耕,等.灰色系统理论及其应用[M].北京：科学出版社,1999：105-112.

The forecasting of monthly electricity demand in city based on grey markov model

QIAO Song⁃shan1,ZHANG Jian⁃jun2
（1.Zhongyuan University of Technoloy,Zhengzhou 450007,China;2.Henan Agriculture University,Zhengzhou 450002,China）

The traditional grey model only reflects the gener⁃al trend of the monthly electricity demand while failing to reflect the characteristics of the monthly electricity demand with seasonal fluctuation.The grey markov modified model based on the markov theory is proposed,the markov correction coefficient is introduced and is added the dimension information in the model.The problem of the forecasting of monthly electricity demand with double trends is researched in this paper.The example show that the markov mod⁃ified model improve the accuracy of prediction comparing with the traditional grey methods.

monthly electricity demand;grey theory;markov theory;forecasting accuracy

TM715；N941.5

A

1009-1831（2013）01-0011-04

2012-09-11

乔松珊(1978)，女，河南许昌人，硕士，讲师，主要从事应用数学方面研究；张建军（1980），男，河南开封人，研究生，讲师，现从事数理统计方面的研究。

河南省教育厅人文社科研究项目（2011-QN-220）