三维角链锁碳纤维机织物拉伸应变率效应和失效机理

胡杭君，侯仰青，孙宝忠

（东华大学 纺织学院，上海 201620）

三维角链锁碳纤维机织物拉伸应变率效应和失效机理

胡杭君，侯仰青，孙宝忠

（东华大学 纺织学院，上海 201620）

三维角链锁碳纤维机织物准静态拉伸力学性能采用MTS 810型材料测试系统测试，而其在不同高应变率下的拉伸力学性能使用自行设计分离式霍普金森拉杆装置进行测试.通过比较不同应变率下的织物拉伸力学性能，分析应变率对三维结构织物拉伸性能的影响.试验结果表明三维角链锁碳纤维织物是应变率敏感材料，其拉伸弹性模量和失效强度随应变率增加而减小，而断裂应变随着应变率增加而增加.三维角链锁碳纤维机织物拉伸力学性能的应变率效应可由应力波在织物特殊结构中传递来解释.此外，通过分析试验数据建立材料冲击拉伸力学参数与应变率之间的回归方程，结果表明拟合曲线与试验结果具有很好的一致性.

三维角链锁碳纤维机织物；应变率效应；动态拉伸力学性能；应力波；回归方程

三维角链锁机织物由伸直纬纱在厚度方向接结多层经纱构成，该织物结构增强复合材料比层压复合材料具有更高的抗分层性能和冲击阻抗.准确表征三维角链锁织物拉伸应变率效应可对复合材料冲击性能精确设计提供数据依据.

对纤维和纤维束冲击拉伸目前已有不少研究，如超高相对分子质量聚乙烯纤维［1－2］、玻璃纤维［3－4］、对位芳香族聚酰胺纤维［5－8］、碳纤维［3，9］和玄武岩纤维［10］等，除碳纤维外，上述纤维在应变率为0.001～3 000s－1范围内的力学性能均表现出不同的应变率相关性.

由纤维束经一定交织形成具有稳定结构的织物，是实现纤维材料最终用途的重要方式.二维平纹织物是研究织物冲击拉伸性能的主要织物种类.如文献［11］采用分离式霍普金森拉杆测试Twaron CT 716织物在应变率为0.01～550s－1范围内的拉伸力学性能，结果表明，Twaron织物对应变率敏感，织物的拉伸强度和拉伸模量均随应变率增加而降低，同时通过建立材料黏弹性本构模型来揭示材料拉伸破坏机理.文献［12］测试Kevlar 49和Zylon织物在低应变率下拉伸力学性能，研究表明这两种织物在不同低应变率下对应变率具有相关性.文献［13］测试Kevlar 49平纹织物在应变率为25～170 s－1范围内的拉伸力学性能，结果发现Kevlar 49平纹织物拉伸力学性能参数（杨氏模量、拉伸强度、失效应变和断裂韧性）均随应变率增加而增大.文献［14］采用分离式霍普金森拉杆系统测试Kevlar 49平纹织物在应变率为0.000 1～1 500s－1范围内的拉伸力学响应，研究结果显示Kevlar 49平纹织物拉伸模量对应变率不敏感，失效强度对应变率是否敏感需进一步通过试验进行验证.

本文采用MTS 810型材料测试系统测试三维角链锁碳纤维机织物在准静态下拉伸力学性能，并使用自行设计分离式霍普金森拉杆装置测试三维角链锁碳纤维机织物动态拉伸力学性能，通过比较不同高应变率下织物拉伸力学性能，且由试验数据建立织物拉伸力学参数与应变率间的回归方程，分析织物拉伸力学性能的应变率效应，从而揭示织物结构对拉伸破坏的影响和失效机理.

1 试验与材料

1.1 材料与试样准备

三维角链锁机织物示意图如图1所示.由图1可知，织物由经纱和纬纱两个系统构成，其中，纬纱平行排列无屈曲，经纱以一定角度沿材料结构的厚度方向衬入.每一层中，相邻两根经纱的屈曲波动状态相反，由此形成对材料厚度方向上任意两相邻纬纱层强有力的束缚作用，从而维持织物整体结构的稳定性.以此织物结构作为增强体相形成的树脂基复合材料具有高强、高模、高层间剪切强度，以及大面积区域承受加载、吸收能量等诸多优势.三维角链锁碳纤维机织物由日本东丽®（Toray）T300 3K碳纤维束织造，纤维束和织物参数分别如表1和2所示.织物的表面图和截面图如图2所示.用于测试的试样尺寸为100mm×10mm×1.8mm（长×宽×厚）.

图1 三维角链锁机织物示意图Fig.1 Schematic diagram of 3－D angle－interlock woven fabric

表1 T300 3K碳纤维束性能参数Table 1 Properties of T300 3Kcarbon fiber tow

表2 三维角链锁碳纤维机织物参数Table 2 Specifications of 3－D angle－interlock woven carbon fabric

图2 三维角链锁碳纤维机织物照片Fig.2 Photographs of 3－D angle－interlock woven carbon fabric

1.2 准静态拉伸测试

三维角链锁碳纤维机织物沿纬向准静态拉伸在MTS 810型材料测试仪（如图3所示）上完成，其中，拉伸速度为2mm／min（应变率为0.001s－1），测试夹持长度为10mm.

图3 MTS 810型材料测试仪Fig.3 Photograph of MTS 810material test system

1.3 动态拉伸测试

三维角链锁碳纤维机织物在高应变率下沿纬向拉伸试验在自行设计分离式霍普金森拉杆装置（如图4所示）上完成.图5为分离式霍普金森杆示意图，它简单揭示了整个动态拉伸过程和数据采集方法.动态冲击过程中因应力波传递到应变片而使应变片产生变形，从而记录下两列电阻－时间信号，经超动态应变仪放大、转换，并由数据采集卡采集，最终得到两个电压－时间信号.基于一维应力波理论、应变均匀性假设，可得到织物试样应力、应变和应变率方程［15］如式（1）～（3）所示.

图4 自行设计的分离式霍普金森拉杆装置图Fig.4 Photograph of self－designed split Hopkinson tension bar apparatus

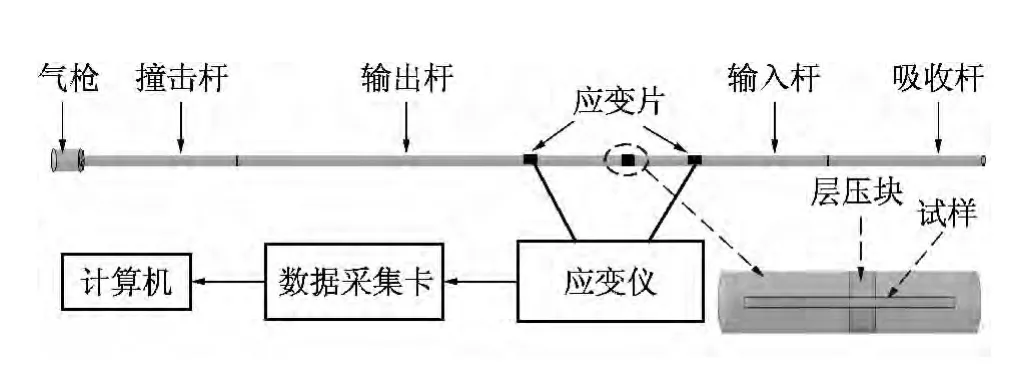
图5 分离式霍普金森拉杆示意图Fig.5 Sketch diagram of split Hopkinson tension bar apparatus

2 试验结果与讨论

2.1 准静态下织物拉伸结果

三维角链锁碳纤维机织物在准静态下沿纬向拉伸载荷－位移曲线如图6所示.由图6可以看出，三维角链锁碳纤维机织物在准静态下拉伸力学性能基本呈线性趋势.从载荷－位移曲线中可以计算得出，三维角链锁碳纤维机织物在准静态下拉伸模量为67.4MPa，失效载荷为8.2kN，断裂应变为8.9%.通过对图6中载荷－位移曲线积分得到三维角链锁碳纤维机织物在准静态下拉伸吸收能量－位移曲线，如图7所示.由图7可以看出，在拉伸初始阶段，织物拉伸吸收能量增加缓慢；随着位移的增加，拉伸吸收能量增加逐渐加快.织物在准静态下的拉伸断裂吸收能量为4.75J.图8为三维角链锁碳纤维机织物在应变率为0.001s－1下拉伸后断裂形态图.由图8可以看出，织物在准静态拉伸断裂后，经纱没有明显的移动或变形.

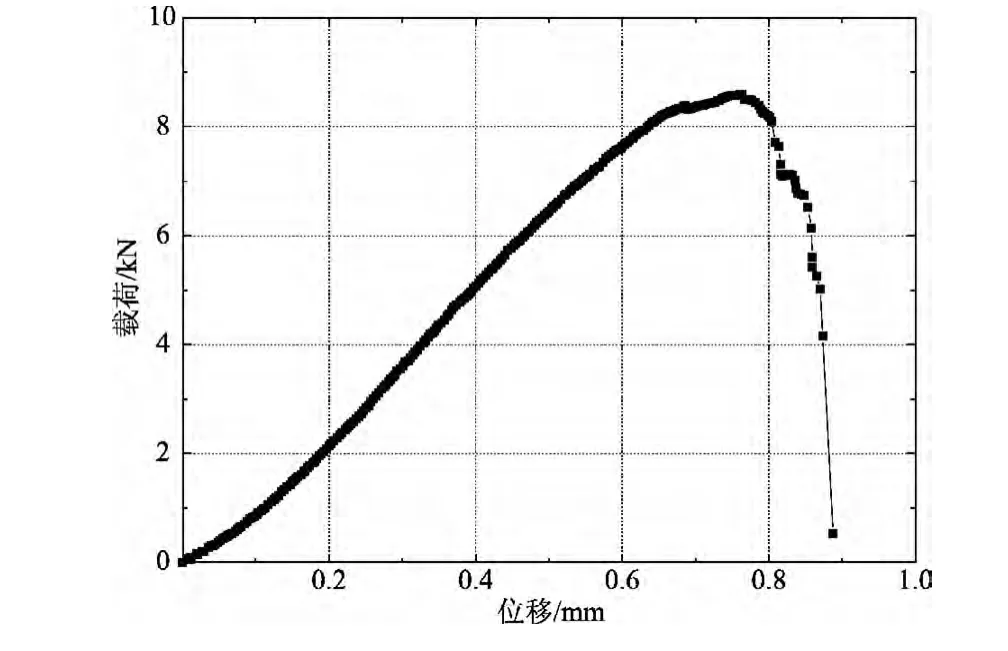
图6 准静态下三维角链锁碳纤维机织物载荷－位移曲线Fig.6 Load－displacement curve of 3－D angle－interlock woven carbon fabric under quasi－static

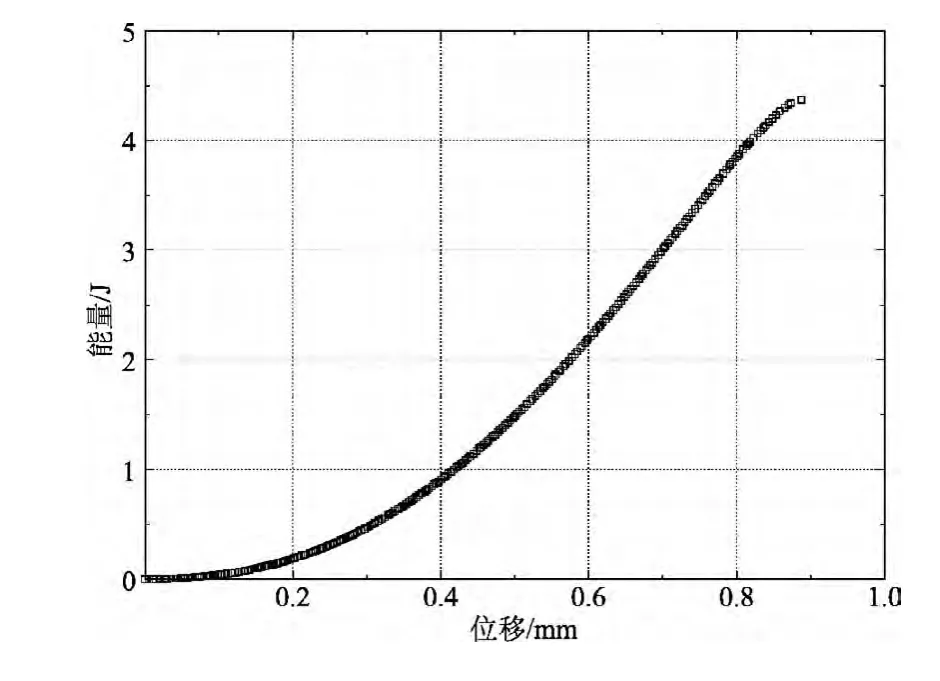
图7 准静态下三维角链锁碳纤维机织物拉伸吸收能量－位移曲线Fig.7 Energy absorption－displacement curve of 3－D angleinterlock woven carbon fabric under quasi－static

图8 准静态下三维角链锁碳纤维机织物拉伸断裂形态图Fig.8 Tensile fracture morphology of 3－D angle－interlock woven carbon fabric under quasi－static

2.2 不同高应变率下织物拉伸结果

图9为三维角链锁碳纤维机织物在4种不同高应变率下沿纬向拉伸载荷－位移曲线.由图9可以看出，三维角链锁碳纤维机织物在不同高应变率下拉伸具有不同的弹性模量、失效强度和断裂应变.三维角链锁碳纤维机织物在不同高应变率下拉伸吸收能量－位移曲线如图10所示.由图10可以看出，当织物拉伸达到相同位移时，其所吸收的能量随应变率增加而减小，且当织物拉伸断裂时，拉伸断裂过程中织物所吸收的总能量也随应变率增加而减小.产生该现象的原因是三维角链锁机织物由5层伸直纬纱和4层屈曲经纱组成，在冲击拉伸过程中，由于每层纬纱与经纱间相互接触及交织状况都不相同，因而不同层纬纱不会同时断裂.应力波会首先传播到纬纱上，接着部分应力波会通过交织点传递到经纱上，使经纱产生宏观运动，如图11所示.随着应变率的增大，经纬纱之间的相互作用加剧，不同纬纱断裂不同时性也增大，从而使织物拉伸失效强度减小.根据织物结构在厚度方向的对称性可知，织物表面两层纬纱会首先断裂，其次中间3层纬纱开始断裂，但要详细揭示瞬时冲击拉伸断裂过程需高速摄影仪辅助.

图9 不同高应变率下三维角链锁碳纤维机织物拉伸载荷－位移曲线Fig.9 Load－displacement curves of 3－D angle－interlock woven carbon fabric under different high strain rates

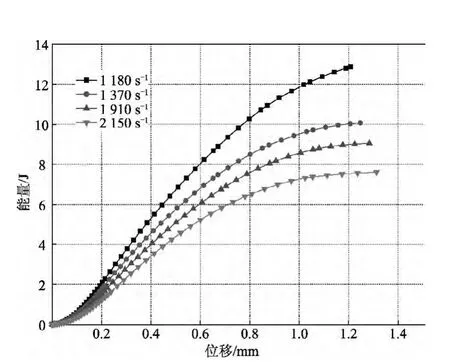
图10 不同高应变率下三维角链锁碳纤维机织物拉伸吸收能量－位移曲线Fig.10 Energy absorption－displacement curves of 3－D angle－interlock woven carbon fabric under different high strain rates

与准静态相比，三维角链锁碳纤维机织物在高应变率加载下的拉伸弹性模量、失效应力和断裂应变都要大很多.通过比较准静态和高应变率下拉伸载荷－位移曲线及断裂形态可知，织物在准静态加载和动态加载下拉伸断裂机理不同.当织物在准静态下被拉伸时，产生的应力波较小，整个拉伸过程中只有微弱的应力波传递到经纱上，经纬纱之间相互作用较小，因此经纱的位移很小，如图8所示.而在高应变率加载下，织物拉伸产生的应力波较强，传播速度较快，经纬纱之间相互作用较强，织物在厚度方向上通过经纱连接，使纬纱之间产生相互联系，从而使织物能承受更大的载荷.整个织物中不同纱线或相同纱线的不同位置处于不同应力状态，导致在部分纱线开始断裂时，应力波还会继续在织物上传递.且经纬纱交织点和接触区域有很强应力波的透射和反射，因此，经纱将产生较大位移，整个织物结构完全发生破坏，如图11所示.

2.3 高应变率下织物拉伸力学参数与应变率之间的关系

图12为三维角链锁碳纤维机织物在高应变率（1 100～2 150s－1）下拉伸力学性能（弹性模量、失效应力和断裂应变）与应变率关系图.由图12可知，织物拉伸断裂应变随应变率的增加而增加，而拉伸弹性模量和失效应力随应变率的增加而减小.因此，三维角链锁碳纤维机织物动态拉伸力学性能对应变率敏感，但已有研究表明碳纤维束为应变率不敏感材料［16－17］，其原因可以归咎于织物具有特殊三维结构.在厚度方向上，织物的每一层都有经纬纱之间的相互作用，所以在高速拉伸过程中，应变波可以通过经纬纱接触点在厚度方向上传递.通过分析试验数据可知，弹性模量、失效应力和断裂应变与应变率有显著的关系，因此，通过线性拟合可以得到织物拉伸力学参数与应变率之间的回归方程，回归方程如下：

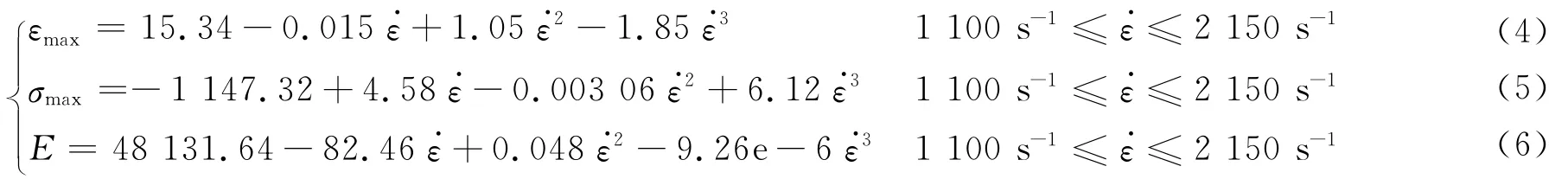
式中：εmax为断裂应变；σmax为失效应力；E为弹性模量；为应变率.

由图12可以看出，回归方程与试验结果有很好的一致性.

图12 不同高应变率下三维角链锁碳纤维机织物力学性能－应变率关系曲线Fig.12 Mechanical properties－strain rate curves of 3－D angleinterlock woven carbon fabric under different high strain rates

3 结 语

（1）三维角链锁碳纤维机织物在高应变率下对应变率敏感，其拉伸弹性模量和失效应力随应变率增加而减小，而断裂应变随应变率的增加而增大.当织物在高应变率加载拉伸达到相同位移时，织物所吸收能量随着应变率的增加而减小，且当织物拉伸断裂时，拉伸断裂过程中所吸收的总能量也随应变率的增加而减小.

（2）准静态下三维角链锁碳纤维机织物拉伸弹性模量、失效应力、断裂应变和拉伸断裂时所吸收的总能量均比在高应变率加载下要小，说明织物在准静态下和高应变率下具有不同的拉伸失效机理，这可以通过三维角链锁机织物特殊结构以及应力波在经纬纱接触区域和交织点处反射和透射来解释.

（3）通过分析试验数据建立了拉伸力学参数与应变率间的回归方程，且回归曲线与试验结果有很好的一致性.该研究工作可以扩展至三维织物复合材料高应变率加载条件下的动态响应设计.

参 考 文 献

［1］CANSFIELD D L M，WARD I M，WOODS D W，et al.Tensile strength of ultra high modulus linear polyethylene filaments［J］.Polymer Communications，1983，24（5）：130－131.

［2］SCHWARZ P，NETRAVALI A，SEMBACH S.Effects of strain rate and gauge length on the failure of ultra－high strength polyethylene fibers ［J］.Textile Research Journal，1986，56（8）：502－508.

［3］WAGNER H D，ARONHIME J，MAROM G.Dependence of the tensile strength of pitch－based carbon and para－aramid fibers on the rate of strain ［C］／／Proceeding of the Royal Society Series A，Mathematical and Physical Sciences.London，1990，428（1875）：493－510.

［4］AMANIAMPONG G，BURGOYNE C J.Statistical variability in the strength and failure strain of aramid and polyester yarns［J］.Journal of Material Science and Technology，1994，29（9）：5141－5152.

［5］FARSI D B，NEMES J A，BOLDUC M.Study of parameters affecting the strength of yarns ［J］.Journal of Physics IV France，2006，134：1183－1188.

［6］TAN V B C，ZENG X S，SHIM V P W.Characterization and constitutive modeling of aramid fibers at high strain rates［J］.International Journal of Impact Engineering，2008，35（11）：1303－1313.

［7］WANG Y，XIA Y M.The effects of strain rate on the mechanical behavior of Kevlar fiber bundles：An experimental and theoretical study［J］.Composites：Part A，1998，11（29）：1411－1415.

［8］WANG Y，XIA Y M.Dynamic tensile properties of E－glass，Kevlar 49and polyvinyl alcohol fiber bundles［J］.Journal of Materials Science Letters，2000，19（7）：583－586.

［9］ZHOU Y X，WANG Y，XIA Y M，et al.Tensile behavior of carbon fiber bundles at different strain rates ［J］.Materials Letters，2010，64（3）：246－248.

［10］ZHU L T，SUN B Z，GU B H.Constitutive equations of basalt filament tows under quasi－static and high strain rate tension［J］.Materials Science and Engineering：A，2010，527（13／14）：3245－3252.

［11］SHIM V P W，LIM C T，FOO K J.Dynamic mechanics properties of fabric armor［J］.International Journal of Impact Engineering，2001，25（1）：1－15.

［12］NAIK D， SANKARAN S， MOBASHER B， et al.Development of reliable modeling methodologies for fan blade out containment analysis part I：Experimental studies ［J］.International Journal of Impact Engineering，2009，36（1）：1－11.

［13］ZHU D，MOBASHER B，RAJAN S D.Dynamic tensile testing of Kevlar 49fabrics［J］.ASCE Journal of Materials in Civil Engineering，2011，23（3）：230－239.

［14］SEIDT J D，MATRKA T A，GILAT A，et al.Tensile behavior of Kevlar 49woven fabrics over a wide range of strain rates［J］.Dynamic Behavior of Materials，2011，99（1）：187－193.

［15］汪洋，夏源明.杆－杆型冲击拉伸试验装置一维试验原理有效性的论证［J］.实验力学，1997，12（1）：126－134.

［16］ZHOU Y X，DAI Z Q，XIA Y M.Tensile mechanical behavior of T300and M40Jfiber bundles at different strain rate ［J］.Journal of Materials Science，2001，36（4）：919－922.

［17］ZHOU Y X，WANG Y，XIA Y M.Experimental study on tensile behavior of carbon fiber and carbon fiber reinforced aluminum at different strain rate ［J］.Applied Composite Materials，2007，14（1）：17－31.

Strain Rate Effect and Failure Mechanism of 3－D Angle－Interlock Woven Carbon Fabric

HUHang－jun，HOUYang－qing，SUNBao－zhong
（College of Textiles，Donghua University，Shanghai 201620，China）

The tensile tests of 3－D angle－interlock woven carbon fabric （3DAWF）were explored under quasi－static（0.001 s－1）loading using a MTS810 material test system，while high speed（up to 2 150 s－1）tests of 3DAWF were conducted using a self－designed split Hopkinson tension bar（SHTB）apparatus.The stress－strain response at various strain rates were obtained，which manifested that 3DAWF was significantly strain rate sensitive.Specifically，the elastic modulus and the maximum stress both decreased with increasing of the strain rate，while the maximum strain increased as the strain rate increased.The strain rate effect of 3DAWF could be reasonably explained by the propagation of the stress wave in this particular fabric architecture.Moreover，a regression formula was established between the mechanical parameters and the strain rate which showed a good agreement with the experimental data.

3－D angle－interlock woven carbon fabric；strain rate effect；dynamic tensile property；stress wave；regression formula

V 258＋.3

A

1671－0444（2013）06－0720－06

2012－07－23

胡杭君（1988—），男，浙江金华人，硕士研究生，研究方向为三维纺织结构复合材料的力学性能.E－mail：2100142＠mail.dhu.edu.cn

孙宝忠（联系人），男，副教授，E－mail：sunbz＠dhu.edu.cn