L1-norm minimization for quaternion signals

Zhang Xu Wu Jiasong，3 Yang Guanyu，3 Lotfi Senahdji Shu Huazhong，3

(1Laboratory of Image Science and Technology， Southeast University， Nanjing 210096， China)(2LTSI， INSERM U 1099， Université de Rennes 1， Rennes 35000， France)

(3Centre de Recherche en Information Biomédicale Sino-français， Nanjing 210096， China)

T he problem of L1-norm minimization plays an important role in the recently developed compressed sensing(CS)theory［1-3］， which is a new approach for data acquisition and has wide applications in the field of signal and image processing.CS has been conventionally used to real input data.Recently， special attention has also been paid to the complex input data such as blind source separation［4］and terahertz imaging［5］.

On the other hand，the theory and application of quaternion or hypercomplex algebra，invented by Hamilton［6］， haveReceivedmuch attention in recent years［7-14］.Ell and Sangwine［7］applied the quaternion Fourier transform to color image processing.Jiang and Wei［9］proposed an algorithm for solving the quaternion least squares problem:

where A∈Qn×m， B∈Qu×m， x∈Qm×1， y∈Qn×1， Q denotes the quaternion number field，and ·2denotes the L2-norm of quaternion vector.The algorithm reported in Ref.［9］was further extended by Jiang et al.［10］to a twodimensional scenario where the inputs are quaternion matrices.Note that the algorithms reported in Refs.［9-10］solve the overdetermined system，that is，n≥mfor measurement matrix A.

In this paper，we consider the recovery problem of quaternion signals for the case wheren≤m，that is，we deal with the underdetermined linear system with measurement matrix A，which is quite different from that of(1).We will do that by solving an L1-norm minimization problem.To the authors'knowledge，the L1-norm minimization problem for the quaternion signals has not yet been investigated.Winter et al.［4］converted the L1-norm minimization of complex signals to the secondorder cone programming(SOCP)，which was then solved by SeDuMi software［15］.In this paper，we extend the algorithm［4］to the quaternion signals with and without noise contamination，which are，respectively，defined by the following two optimization problems:

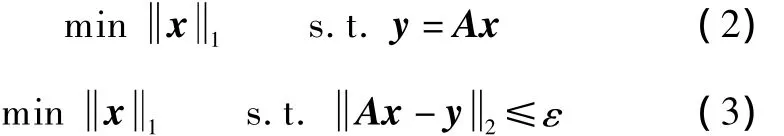
where·1denotes the L1-norm of the quaternion vector and ε is the noise penalty level for noise term e in noise measurements y=Ax+e.

1 Definitions

A quaternionqis a hypercomplex number which consists of one real partR(q)and three imaginary partsI(q)，J(q)andK(q)as follows:

whereR(q)，I(q)，J(q)，K(q)∈R;andi，jandkare three imaginary units obeying the following rules:

The conjugate and modulus of a quaternion are，respectively，defined as*

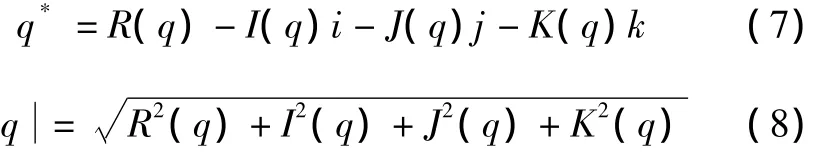
We also define

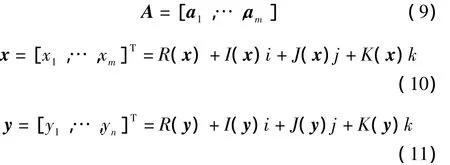
The Lp-norm of a quaternion vector x is given by

2 Method

In this section，we derive an algorithm based on SOCP for L1-norm minimization problems dealing with quaternion signals.

2.1 Noiseless case

The minimization problem shown in(2)is equivalent to its epigraph form:

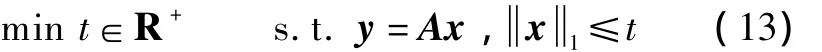
By introducing auxiliary variablestr∈R+，wherer=1，2，…，mand R+denotes the positive real number field，the second constraint x1≤tcan be decomposed into a set ofmconstraints After some manipulation，(15)can be written as

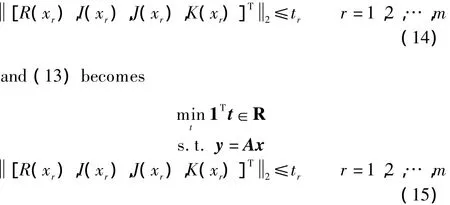
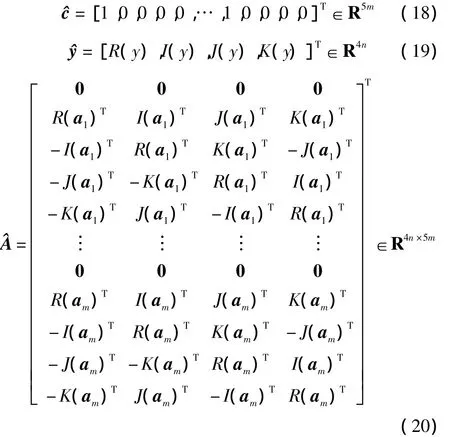
2.2 Noise case

Similar to the previous case，the minimization problem shown in(3)can be reformulated as

The first inequality constraint of(21)can be written as

or equivalently

where

Here(z，z0，z1)belongs to a rotated second-order cone.Taking the linear relationship among^x，z，z0and z1into account，we can obtain a linear constraint:where

And the original problem can be turned into a second-order cone problem as

(16)and(25)are the standard forms of the SOCP problem and can be solved by using several mature toolboxes，such as SeDuMi［15］.Then，we can easily obtain the recovered quaternion signal xr from^x or~x.

3 Numerical Experiments

In a noiseless scenario，just as in Ref.［1］，we present numerical experiments that indicate empirical bounds on sparsitys(time domain support of the input signal)relative ton(the number of measurements)for perfectly recovering a quaternion signal x.The results can be seen as a set of practical guidelines for situations in which one expects perfect recovery from random Gaussian quaternion measurements using SOCP.Numerical experiments are carried out as follows:

1)Annbym(m=512 is the length of input signal，nis the number of measurements)random Gaussian measurement matrix A∈Qn×m(n≤m)is produced with random entries sampled from an independent and identically distributed(i.i.d.)Gaussian process with a zero mean and a variance equaling 1(in quaternion L2-norm sense).

2)Sparse quaternion input signal x∈Qm×1is produced by selecting a support set| T| of sizeT=s(sparsity)uniformly at random and sampling a vector x on T with i.i.d.Gaussian entries.

3)Quaternion output signal y∈Qn×1is obtained by multiplying A with input x.

4)The vectors，and matrixare constructed as described in(17)to(20).

5)SeDuMi toolbox［15］is called to solve SOCP problem(16)and the error is computed，which is the L2-norm of the difference between the recovered signal xr and the input signal x，i.e.， xr－ x2.

We perform experiments 100 times for each pair ofsandn，then we save these errors and count the number of perfect recovered experiments.The criterion for perfect recovery is chosen as xr－ x2≤10－8.

Fig.1 shows the recovery success rate of 512-length signals with different measurement numbers and sparsity level configurations.The image intensity indicates a success ratio with sparsity levelsand measurements numbern.Fig.2 depicts its cross section at five different values ofn.It can be seen from this figure that forn≥32，the recovery rate is about 80%whens≤n/5 and practically 100% whens≤n/8.These results are very similar to those reported in Ref.［1］which deals with the real signal with lengthm=512.

Fig.1 Recovery experiment for m=512

Fig.2 Cross section of Fig.1 at n=8，16，32，64 and 128

To further illustrate the recovery results，Fig.3 and Fig.4 depict the original quaternion signal x and its corresponding recovered signal xr.In Fig.3，m=512，n=160，ands=60 and the quaternion signal is perfectly recovered.In Fig.4，m=512，n=160，ands=120 and in this case the recovery process failed.

Fig.3 Illustration of successful recovery of quaternion signal with sparsity level s=60.(a)Original signal，r part;(b)Recovered signal，r part;(c)Original signal，i part;(d)Recovered signal，i part;(e)Original signal，j part;(f)Recovered signal，j part;(g)Original signal，k part;(h)Recovered signal，k part

In the noise case，the original signal x and measurement matrix A are generated as in the noiseless casen=160，m=512，s=60.The measurements are corrupted by the white quaternion Gaussian noise vector comprised of i.i.d.Gaussian variables with mean 0 and variance σ2，so the squared L2-norm of noise vector e22is a chisquare random variable with mean 4nσ2and standard deviationσ2.Since the probability that e22exceeds its mean plus two or three standard deviations is small，here we choosetheconstraintparameterεtobeε=

σ

Fig.4 Illustration of failed recovery of quaternion signal with sparsity level s=120.(a)Original signal，r part;(b)Recovered signal，r part;(c)Original signal，i part;(d)Recovered signal，i part;(e)Original signal，j part;(f)Recovered signal，j part;(g)Original signal，k part;(h)Recovered signal，k part

We carried out ten recovery trials at different noise levels，and the average recovery errors with respect to corresponding noise strengths in those experiments are shown in Tab.1.The results in Tab.1 show that the proposed recovery algorithm is robust to noise contamination，and the recovery errorsare abouttwo timesthe noise strengths.An example of a recovery of sparse signals with noisy measurements is shown in Fig.5(σ =0.5).

Tab.1 Recovery errors with respect to corresponding noise strengths

4 Conclusions and Future Work

Fig.5 Example of sparse signal recovery with noisy measurements.(a)Original signal，r part;(b)Recovered signal，r part;(c)Original signal，i part;(d)Recovered signal，i part;(e)Original signal，j part;(f)Recovered signal，j part;(g)Original signal，k part;(h)Recovered signal，k part

In this paper，we propose an algorithm for solving the L1-norm minimization problem of quaternion signals，which is converted to SOCP and then solved by SeDuMi software.Numerical examples are provided to illustrate the feasibility of the algorithm.The results can be viewed as a set of practical guidelines for situations where one expects perfect or stable recovery from random Gaussian quaternion measurement matrix information using SOCP.The main advantage of the proposed algorithm is that when converting the quaternion values optimization to that of real values，many mature toolboxes can be applied.However，the converting process decouples the real and imaginary parts of the quaternion signals and no prior phase information is exploited.Further research includes:1)Considering the prior phase information in quaternion signals optimization［5］;2)Extending the quaternion signal vector L1-norm minimization algorithm to that of quaternion matrix nuclear norm minimization，that is，quaternion matrix completion［16］;3)Studying the problem of robust quaternion principal component analysis［17］.

［1］Candès E，Romberg J，Tao T.Robust uncertainty principles:exact signal reconstruction from highly incomplete frequency information［J］.IEEE Transactions on Information Theory，2006，52(2):489-509.

［2］Donoho D.Compressed sensing［J］.IEEE Transactions on Information Theory，2006，52(4):1289-1306.

［3］Candès E，Romberg J，Tao T.Stable signal recovery from incomplete and inaccurate measurements［J］.Communications on Pure and Applied Mathematics，2006，59(8):1207-1223.

［4］Winter S，Kellermann W，Sawada H，et al.MAP-based underdetermined blind source separation of convolutive mixtures by hierarchical clustering and L1-norm minimization［J］.EURASIP Journal on Advances in Signal Processing，2007，2007(1):81.

［5］Yu S，Khwaja A S，Ma J.Compressed sensing of complex-valued data［J］.Journal on Signal Processing，2012，92(2):357-362.

［6］Hamilton W R.On quaternions［C］//Proceedings ofRoyal Irish Academy.Dublin，Ireland，1844:1-16.

［7］Ell T，Sangwine S.Hypercomplex Fourier transforms of color images［J］.IEEE Transactions on Image Processing，2007，16(1):22-35.

［8］Vía J，Ramírez D，Vielva L.Properness and widely linear processing of quaternion random vectors［J］.IEEE Transactions on Information Theory，2010，56(7):3502-3515.

［9］Jiang T，Wei M.Equality constrained least squares problem over quaternion field［J］.Applied Mathematics Letters，2003，16(6):883-888.

［10］Jiang T，Zhao J，Wei M.A new technique of quaternion equality constrained least squares problem ［J］.Journal of Computational and Applied Mathematics，2008，216(2):509-513.

［11］Vía J，Palomar D P，Vielva L，et al.Quaternion ICA from second-order statistics［J］.IEEE Transactions on Signal Processing，2011，59(4):1586-1600.

［12］Javidi S，Took C C，Mandic D P.A fast independent component analysis algorithm for quaternion signals［J］.IEEE Transactions on Neural Networks，2011，22(12):1967-1978.

［13］Le Bihan N，Buchholz S.Quaternionic independent component analysis using hypercomplex nonlinearities［C］//7th International Conference on Mathematics of Signal Processing.Cirencester，UK，2006.

［14］Le Bihan N，Sangwine S J.Quaternion principal component analysis of color images［C］//International Conference on Image Processing.Barcelona，Spain，2003:808-812.

［15］Sturm J F.Using SeDuMi 1.02，a MATLAB toolbox for optimization over symmetric cones［J］.Optimization Methods and Software，1999，11(1):625-653.

［16］Candès E，Recht B.Exact matrix completion via convex optimization［J］.Foundations of Computational Mathematics，2009，9(6):717-772.

［17］Candès E，Li X，Ma Y，et al.Robust principal component analysis?［J］.Journal of ACM，2011，58(3):1-37.