空间网络多路径路由算法﹡

朱 超， 洪佩琳， 卢汉成， 张林杰， 阎长江

（①中国科学技术大学 电子工程与信息科学系信息网络实验室，安徽 合肥 230027；②军用通信网信息传输与分发技术国防科技重点实验室，河北 石家庄 050081）

0 引言

空间网络通信相关技术近年来得到越来越多的人关注[1-2]。不同于地面通信网络,空间网络通信[3]具有距离远、延时大、周期性间歇连接以及误码率高等特点。传统的路由协议并不能直接适用于空间网络。因此提出新的适用于空间网络环境的路由协议是十分必要的。

目前，针对空间网络的路由算法主要有：ASCOT[4]、S-OSPF[5]、RADSCN[6]、CGR[7]、ECGR[8]、SQRA[9]等路由协议。其中ASCOT是一种以数据为中心基于节点位置的空间网络路由协议，其中以数据为中心实现了与其它邻近网络的互通，基于节点位置可以适应空间网络拓扑结构动态变化的特点。S-OSPF协议一种分等级的路由协议，将空间网络分成三个区域，不同的区域使用不同的路由协议。RADSCN是一种最大吞吐量算法，基于联通时序图计算出一条吞吐量最大的路径。CGR协议充分利用了空间网络节点连接可预测性这一特点，网络中节点的捆绑层可预测其它节点的当前状态和节点间连接时刻表，从而进行有效的路径选择。文献[10]验证了可以将CGR算法应用于邻地空间中。ECGR是对CGR协议的改进，使用Dijkstra算法代替了CGR中回溯法，大大减少了算法的复杂度。文献[11]在CGR基础上提出了多目标路由算法MD-CGR。SQRA提出了一种满足不同业务的空间路由算法。

空间网络节点采集的实验数据非常庞大，但是网络的数据传输能力又十分有限，如果不能有效的传输这些数据，会给网络造成沉重的负担。目前空间网络路由算法主要都是单路径路由算法，并不能充分利用空间网络的宝贵资源。文献[12]提出了一种空间多路径路由算法，该算法使用多条吞吐量最大的路径来传输数据，但是算法复杂度高达并不适用于节点计算能力较弱的空间网络，此外，该算法还忽略了空间长时延传输的特点。空间网络多路径最大吞吐量的路由算法（SMMT, Space Multi-path and Max Throughput Routing Algorithm）是对

最小费用最大流算法的改进，在保证传输时延性能要求的基础上，为间歇性网络提供多条端到端的连接，充分利用了空间网络的宝贵资源。

1 系统模型

在空间网络中，每个节点都在各自的轨道上周期性运行，节点之间间歇性连接，通过星历表[4]或者节点轨道参数[5]就可以实时准确预测出每个节点的位置信息和节点间的连接状态。

如图1所示，空间网络拓扑图G由4个矩阵表示，分别为：连接开始矩阵连接结束矩阵传输时延矩阵和传输带宽矩阵

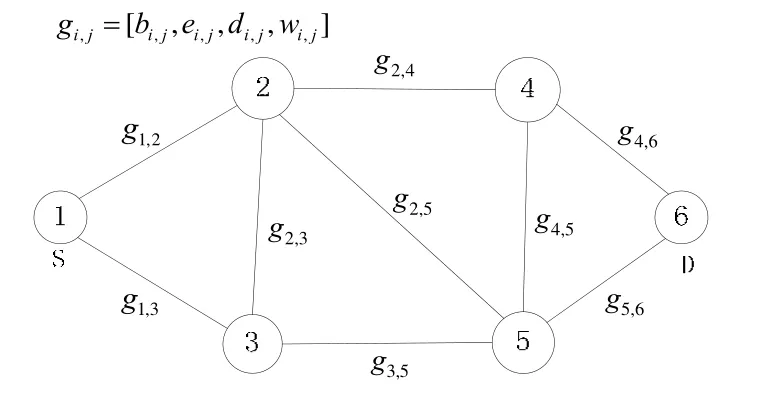
图1 空间网络拓扑

2 SMMT路由算法

SMMT路由算法使用存储转发机制，构造多条非实时的端到端的连接。算法主要包含两个步骤：①使用改进的Dijkstra算法[5]寻找最小费用路径；②使用改进的最大流算法查找最大吞吐量路径。首先使用改进的 Dijkstra算法主要用于寻找单条最短时延路径，在时延约束得到保证的前提下，使用改进最大流算法查找多条符合条件的路径。改进的最大流算法又主要分为瓶颈参数计算和残留网络构造两个部分。

2.1 SMMT路由选择算法

算法1:SMMT路由选择算法；

输入：一段时间 T内的网络拓扑图（如图 1所示）；

输出：点到点的多路径路由表；

①while（ture）do begin

a)使用改进的 Dijkstra算法查找一条源节点到目的节点的最短时延路径；

b)如果不存在，则跳出循环，寻路结束；

c)如果数据到达目的节点的时间已经大于数据包的生存时间，则跳出循环，寻路结束；

d)计算已找出路径的瓶颈参数；

e)按照2.3节构造间歇性残留网络；

end

②整合各条已找出的单条路径，构造多路径路由表。

SMMT算法是一个循环迭代的过程，不断的通过改进的 Dijkstra算法和最大流算法查找出网络中多个最短时延路径，直到网络中不存在可行的单条路径为止。SMMT算法最终可为用户计算出多条满足Qos需求的传输路径。

2.2 改进的Dijkstra算法

ASCOT协议采用改进的适用空间网络的Dijkstra算法[4]查找最短时延路径。改进的 Dijkstra算法需要更新数据到达每个节点的时间，这里使用矩阵 []nA 表示。

在空间网络中，节点之间成间歇性连接，如图 2所示，链路,ikl 的连接开始时间为,ikb ，连接结束时间为,ike ，数据在两节点之间的传输时延为,ikd 。假设数据在ia时刻到达节点i，那么数据从节点i通过节点k到达节点j的情况可分为图2中三种情况：数据到达时链路处于联通状态、数据到达时链路处于等待联通状态和数据到达时链路联通时间不足以传输数据。根据式(1)可以得出数据到达每个节点的时间，然后使用 Dijkstra算法求出端到端的最短时延路径[4]。

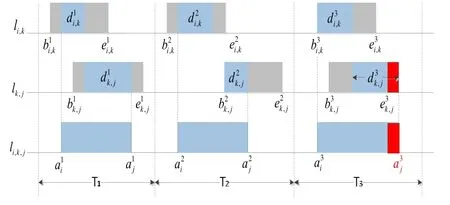
图2 间歇性连接到达时间

2.3 改进的最大流算法

多路径最大吞吐量算法是对最小费用最大流算法[13]的改进，其中最小费用算法参考 2.2节。不同于最大流算法，SMMT算法提出了新的路径瓶颈参数计算方式和空间间歇性残留网络概念。

2.3.1 瓶颈参数的计算

节点i和节点k在时间 T内的链路连接的开始时间为,ikb ，结束时间为,ike ，传输时延为,ikd 和链路带宽为,ikw ，则链路可用的有效传输时间,ikt 为：

假设使用改进的 Dijkstra算法求出的可行的最短时延路径,SDP 为定义路径的瓶颈参数分别为瓶颈传输时间mint 、瓶颈带宽和瓶颈吞吐量minTh 。首先，可以根据每条链路的带宽计算出整条路径,SDP 的瓶颈带宽：

然后根据数据达到节点ik的时间ika，计算出每条链路的有效传输时间，这时分为两种可能：

同理可以计算出路径,SDP 上所有链路的有效传输时间。那么，路径,SDP 的瓶颈传输时间为：

2.3.2 间歇性残留网络构造

从2.3.1节可以得出路径,SDP 的瓶颈传输时间、瓶颈带宽和瓶颈吞吐量，SMMT算法是一个循环迭代的过程，那么每一次间歇性残留网络的构造是由原始网络去除上一次计算出的单路径已经占用的时间和带宽而得到的。更新后的残留网络的相关参数为：

更新间歇性残留网络之后继续按照改进的Dijkstra算法查找下一条可行路径，直到残留网络中不存在可行的单条路径。

对于给定的网络，假设在时间T内一共执行了M次最小费用路由算法，每次获得的瓶颈吞吐量为mTh，那么SMMT算法在时间T内的网络平均吞吐量为：

图3 残留链路

2.4 SMMT算法正确性分析

2.5 SMMT算法复杂度分析

如果给定的网络中有V个节点，E条边，在时间T内的最大吞吐量为maxTh ，由2.4节可知，SMMT算法最多执行maxTh 次最小费用路由算法，使用改进的 Dijkstra算法查找最小费用路径的时间复杂度为处理间歇性残留网络时间复杂度为 ()O E，那么整个 SMMT算法时间复杂度为

3 仿真实验

空间网络通信可分为邻地空间通信和深空网络通信,分别使用 Opnet仿真软件构造了这两种场景,并对SMMT算法和ASCOT、S-OSPF协议进行了仿真分析。

图4为使用Opnet构造的邻地空间通信仿真场景，该场景由7个卫星节点和一个地面固定节点组成，7个卫星节点的高度分别为10 000 km（Sa10，Sa11，Sa12）、20 000 km（Sa20，Sa21，Sa22）和36 000 km（Geo_beijing）。地面节点部署在北京地区，每个节点的通信范围为50 000 km。图5为使用Opnet构造的深空通信仿真场景，该场景由8个节点构成，分别为火星节点、地球节点、地球 L4、L5节点、金星L4、L5节点和水星L4、L5节点。每个节点的通信范围为1.5AU。

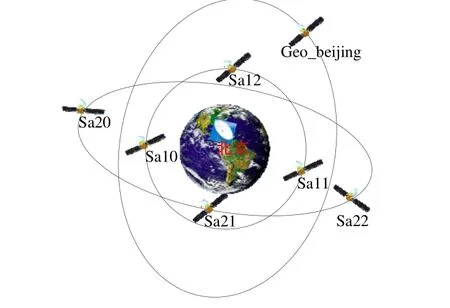
图4 邻地空间仿真场景

图5 深空通信仿真场景

吞吐量：在邻地空间通信场景中，同步卫星为源节点，地面节点为目的节点，仿真持续时间为180个小时，在深空通信网络场景中，火星为源节点，地球为目的节点，仿真持续时间为3 500个小时。从图6和图7中可以看出，由于SMMT算法使用多条路经传输数据包，SMMT算法的吞吐量比ASCOT和 S-OSPF算法都有了明显的提升，其中邻地空间环境提升了约212%，深空通信环境提升约90%。

图6 邻地空间网络吞吐量

图7 深空通信网络吞吐量

传输时延：图 8为在两种仿真环境下分别使用SMMT、ASCOT和S-OSPF三种算法传输相同大小数据包（邻地空间为50 Mb，深空通信为500 Mb）所消耗的传输时延对比图。从图中可以看出，由于SMMT算法具有较大的网络平均吞吐量，因此传输相同大小数据包消耗的时延明显小于另外两种算法。

仿真耗时：图9为在两种仿真环境下分别使用SMMT、ASCOT和S-OSPF三种算法仿真相同的周期（邻地空间为1周，深空通信为20周）所消耗的仿真时延，由于SMMT算法在提高吞吐量的同时也增加了算法的复杂度，因此该算法的开销最大，耗时也最多。S-OSPF算法因为要经常发送数据包来广播节点的轨道信息，开销就比较大，耗时次之。从时间上来看，ASCOT每次根据预测只需要计算一条最短路径，算法耗时最少。

图8 传输时延

图9 仿真耗时

4 结语

基于空间环境的多路径路由算法—SMMT是对最小费用最大流算法的改进，适用于空间间歇性连接网络。仿真可以表明，SMMT算法使用多条路径传输数据，有效的保证了数据包的传输时延并且明显的提高了网络的吞吐量，使得空间网络的宝贵资源得到了充分的利用。

[1] 尹志忠,陈静毅,周贤伟.美军卫星通信系统的发展及其技术研究[J].通信技术,2009,42(11)：55-58.

[2] 吴晓光,雷菁,黄英.CCSDS分包遥控协议分析[J].信息安全与通信保密,2010(11)：28-30.

[3] MARCHESE M. Interplanetary and Pervasive Communications[J]. Aerospace and Electronic Systems Magazine,IEEE,2011,26(02)：12-18.

[4] GNAWALI O, POLYAKOVT M, BOSE P, et al. Data Centric,Position-based Routing in Space Networks[C]//Aerospace Conference, 2005 IEEE.[s.l.]： IEEE, 2005：1322-1334.

[5] BANTAN N,KKAN J. Space OSPF： an Area Hierarchic Routing Protocol for Routers in Motion[C]//25th AIAA International Communications Satellite Systems Conference.Seoul, South Korea, 2007： 10-13.

[6] 李红艳,杨光祥,王文龙.一种最大吞吐量的深空通信网络路由算法[J].西安电子科技大学学报,2012,39(01)：92-97.

[7] BURLEIGH C S. Contact Graph Routing[S]. IRTF,Internet-Draft draft-burleigh-dtnrg-cgr-00,Dec 2009.

[8] SEGUÍ J, JENNINGS E, BURLEIGH S. Enhancing Contact Graph Routing for Delay Tolerant Space Networking[C]// Global Telecommunications Conference (GLOBECOM 2011), 2011 IEEE.[s.l.]： IEEE,2011：1-6.

[9] 韦娟,王丹丹.空间因特网的路由技术研究[J].通信技术,2010,43(12)：29.

[10] CAINI C, FIRRINCIELI R. Application of Contact Graph Routing to LEO satellite DTN Communications[C]//Communications (ICC), 2012 IEEE International Conference.[s.l.]： IEEE, 2012：3301-3305.

[11] BIRRANE E, BURLEIGH S, KASCH N. Analysis of the Contact Graph Routing Algorithm： Bounding Interplanetary Paths[J]. Acta Astronautica,2012(75)：108-119.

[12] 李红艳,胡云,李建东,等.基于连通时序的多路径路由选择方法：中国,CN102316546A[P]. 2012-01-11.

[13] CORMEN H T,LEISERSON E C,RIVEST L R,et al.算法导论[M].潘金贵,顾铁成,李成法,等译.北京：机械工业出版社,2006：396-425.