人教A版“椭圆的简单几何性质”教材研读
2013-09-17安徽省六安中学陆学政刘清尧邮编237005
安徽省六安中学 陆学政 刘清尧 (邮编:237005)
备好课是上好课的先决条件,而教学设计是备课的一种现代发展,是教师的基本功,也是制约教师专业发展的关键要素.精心备课(设计)是精致教学的源泉,是教师提高课堂教学能力的首要途径,其中的一项重要工作就是研读教材.这既是一个从宏观角度领会教材的学科特点、确立教材的地位作用的过程,又是一个从微观角度揣摩教材的编写意图、品味教材的脉络结构的过程,也是一个从操作角度凸现教学的重点难点、分析学生的实际情况、酝酿教学的具体策略的过程.
恰逢笔者之一的刘清尧老师准备开设校级公开课,课题是人教A版选修2-1“椭圆的简单几何性质”,以下就是笔者研读教材时的主要思考.
1 “椭圆的简单几何性质”的地位与作用
(1)从学科特点的角度来看.解析几何的基本问题之一是根据曲线的方程研究曲线的几何性质,“椭圆的简单几何性质”则是学生第一次较为系统地学习在解析几何中如何用代数方法研究曲线性质,既包括研究哪些方面的性质,也包括利用何种方法手段进行研究;既有形的直观,更有数的严谨.这对后续根据方程研究双曲线、抛物线乃至一般曲线的几何性质都具有“示范”与“标杆”作用.应在这个高度上整体把握本节课的教学.
(2)从知识方法的角度来看.一方面,椭圆的基本量a、b、c、e被赋予了简明的几何意义,便于从不同的侧面把握椭圆的图形特征,椭圆的几何性质与其它知识相联系,对于研究圆锥曲线中的范围、最值等问题都有重要意义;另一方面,本节内容蕴含了函数观点、不等式方法、方程思想、变量代换、数形结合等基本数学思想方法,典型而丰富,教学时应“小中见大”,适时提炼上述思想方法,提升学生的数学素养.
(3)从学生发展的角度来看.对椭圆简单几何性质的研究有利于培养学生观察、分析、抽象概括、推理论证、数形结合等数学能力,有利于培养学生严谨的数学态度和思维习惯.教学时应立足于引导学生自己提出要研究的问题、确定研究的方法、评价研究的成果、完善研究的过程,以促进学生发展的最大化.
2 “椭圆的简单几何性质”教材研读
2.1 第43页正文前两段及旁白
研读这一段教材,可以得出对本节课的两点总体认识:
(1)本节课学习的直接基础是椭圆的定义(几何特征)及椭圆的标准方程,任务是利用椭圆的标准方程研究它的几何性质,这恰恰涵盖了解析几何研究的两个主要问题:根据条件求曲线方程,通过方程研究曲线性质.
(2)由于是初次研究曲线的几何性质,学生往往对研究哪些方面不甚了解,难以整体把握具体的研究角度,教师应发挥自身的主导作用,帮助学生明确:曲线的几何性质,一般包括曲线的形状、大小、对称性、位置等,并且是利用曲线的方程进行研究的.
因此,引入新课时,教师要让学生思考:解析几何主要研究哪两个问题?对于椭圆,已经研究了什么,还需要研究什么?如何研究?
2.2 第43页“观察”
研读教材此栏目,可以透视出编者的如下意图:
(1)椭圆的诸多几何性质中,离心率的引入需要研究两个乃至多个椭圆(椭圆的扁平程度是一个相对概念),而范围、对称性、顶点只需研究单个椭圆,根据“由易到难”的原则,本栏目先解决单个椭圆的几何性质问题,离心率的学习则相对独立.
(2)研究椭圆的几何性质,不能直接从方程入手,而是“先直观后抽象”、“先感性后理性”,即先对椭圆的形状从直观上进行观察,“猜想”出椭圆的范围、对称性、顶点等几何性质.又因为“形缺数时难入微”,所以必须“用思维帮助眼睛”,即利用椭圆的标准方程,通过严格的代数推理验证“猜想”.这样做,充分体现了“由形到数,以数促形”,降低了思维的起点和坡度,符合学生的认知基础和思维特点.
因此,利用课件或实物教具,引导学生“观察”、“发现”、“猜想”是必不可少的,教师绝不能包办代替.另外,这些性质被学生“发现”的先后顺序也可能不同,教学中要尽量顺应学生的思路,不能完全拘泥于教材的顺序.
2.3 性质1——“范围”
教材指出,学生“看出”范围是不难的,重点是利用方程(代数方法)去“推导”范围,这里蕴含着两个重要信息:
(2)“以形助数”.在用代数方法得出x、y的取值范围后,要及时回到图形,体会“范围”的几何意义.这里,除了矩形框以外,教材在图中特别标出了椭圆的“特征三角形”——RtΔB2OF2,该三角形以a为斜边长、b和c为直角边长,蕴含了关系式a2=b2+c2以及cos∠OF2B2==e(离心率).四个这样的直角三角形合并后,与矩形框一起构成了椭圆的“内部支架”和“外部框架”,对理解与掌握椭圆的基本知识并形成网络、解决椭圆的有关问题都具有重要的价值.
2.4 性质2——“对称性”
“对称”在很多学生的认知基础中仍然停留在“翻折或旋转后重合”的笼统印象,尚不能自如地从数学的角度对图形对称性的本质进行精确度量.若这个问题得不到有效解决,教材的编写意图则难以实现.事实上,图形对称性的本质是点的对称性,即曲线上任意一点P关于某点(直线)的对称点P′仍在该曲线上.反映在解析几何中,涉及到求对称点的坐标、根据点的坐标是否满足曲线方程来判断该点是否在曲线上,这是处理对称性问题的关键,是教材利用标准方程揭示椭圆为什么关于x轴、y轴和坐标原点对称的根基.
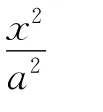
2.5 性质3——“顶点”
这里,虽然涉及了三个概念:顶点、长轴与短轴,但是它们的地位有所不同.具体来说,教材明确指出了椭圆顶点的定义:椭圆与其对称轴的交点(与坐标系选取无关).只是在标准方程下,椭圆的对称轴为x轴、y轴,所以,根据标准方程不难求出椭圆的顶点坐标.而椭圆的长轴与短轴是顶点的“衍生物”,只需结合具体图形能正确指认即可,不必严格定义(定义的语言表述也比较拗口).教材这样处理是合适的,教学中要注意准确把握尺度.
2.6 性质4——“离心率”
离心率的教学是本节的难点.仔细研读教材后,笔者有以下几点认识:
(1)“思考”栏目必要而合理.
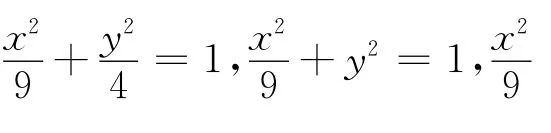
(2)教材中离心率概念的形成显得突兀,第46页的“探究”应提前而不能滞后.

如图,若有学生提出固定a、看b的大小来比较扁平程度时,教师可追问:对于a、b分别都不等的两个椭圆,如何比较呢?学生自然想到用比值,类似于通分那样将分母化为相同后再比较新的分子的大小.另外,教师可适时提示学生:类比用三角函数刻画直线的倾斜程度,在特征三角形(RtΔBFO)中,有;在 RtΔBAO中,也有这些量都可以用来刻画椭圆的扁平程度.然后依据“就简原则”,可以考虑采用.只有这样,才能充分尊重学生的认知规律,让学生的思维“自然地流淌”,才能为提出离心率的概念、也为分析离心率大小与椭圆扁平程度的关系奠定坚实基础.
(3)教材第45页中的“边空”,教学时应充分利用.

限于篇幅,关于教材例习题的研读与教学处理从略.
3 结语
为什么要研读教材?实在是因为教材常常会被教师粗浅地理解,粗放地使用,也因为教材有时会抑制教师教学过程的生动性和主动性.新课改以来,类似于“不是教教材,而是用教材教”这样的口号耳熟能详,但真正能落到实处的教师并不多见,原因在于:要想创造性地使用教材,首先必须深刻地理解与领会教材,没有理解就没有创造.我们既不能盲从教材,更不能对教材的博大精深视而不见,而应提倡对教材的批判性占有.这些,都需要在精心备课的过程中深入地研读教材、品味教材.而现实情况又如何呢?正如华东师范大学周彬教授所说:目前,教师花在批改作业上的时间往往是最多的,至于花在备课(研读教材)上的时间,不是说最少,但实在是亏欠太多,远远配不上其应有的重要程度.
1 普通高中课程标准实验教科书(人教A版选修2-1)[M].人民教育出版社,2009,5
2 普通高中课程标准实验教科书教师教学用书(人教A版选修2-1)[M].人民教育出版社,2009(6)
3 普通高中数学课程标准(实验)[M].人民教育出版社,2003(4)
4 徐光考,蒋燕飞.椭圆离心率的创造性教学[J].中学数学教学参考,2005(1,2)
5 曹才翰,章建跃.中学数学教学概论(第二版)[M].北京师范大学出版社,2008(4)
