一种用于自适应跳频系统的新型交织方法

卢继华，黄承飞，李祥明

(北京理工大学 信息与电子学院，100081 北京)

跳频技术在民用通信中常用于多用户共享频带解决频谱拥挤，且广泛应用于各种现代通信系统中.如自适应跳频用于减轻802.11x 的WLAN(Wireless Local Area Network)系统干扰［1］;在带有RAKE 接收机的TDMA/CDMA 中应用慢跳频来提高系统在多径瑞利衰落信道中的性能［2］;在蓝牙系统中应用增强的自适应跳频来抗定频干扰和变频干扰［3］.在WLAN 的信道绑定技术中使用信道交织技术可以提高误比特率性能［4］.对于跳频(Frequency Hopping，FH)通信系统而言，由于FH 系统本身就是1 个自干扰系统，系统中用户间的干扰比较突出.因此，克服干扰的途径之一是设计出尽可能低汉明互相关性的工程实用码型，途径之二是运用一些消除或减弱干扰的跳频技术，如自适应跳频技术，差分跳频技术等［5］.自适应跳频技术应用广泛，跳频系统在跳频速率很高时对载频的跳变精度及速率均要求很严格，因此设备复杂性相应增加［6］.基于交织的跳频系统将突发错误在译码之前分散开来，将大范围的突发错误转为随机错误，提高差错控制编码的纠错、检错能力，继而提高整个通信系统的性能，降低系统实现的复杂度，并且具有一定的抗干扰能力［7］.而不同的交织方法对整个系统的抗干扰性能的提升是不同的，传统的行列交织虽然实施简单，但是其抗干扰性能并不理想，交织后信息序列之间的相关性依然较大.

本文给出了一种用于自适应跳频系统的新型交织方法，实现了利用素数码族进行交织，满足降低了信息序列相关性的同时，交织延时和存储量的需求也大大降低，降低了高速跳频系统实现时对系统复杂度的需求.分析及仿真结果表明，本文提出的新型交织方法具有优良的抗干扰性能.

1 基于素数码交织的跳频系统

无线通信系统中，用自适应跳频系统来克服人为干扰已有较为广泛的应用［8］，这些系统常采用多进制调制与非相干解调.图1 为本文在基于素数码交织的自适应跳频系统框图［9］，其中虚线框内为本文提出的新型交织方法，包括交织与解交织环节.

图1 自适应跳频通信系统框图

从图1 可以看出，基于素数码交织的自适应跳频系统信号流程如下:随机产生的数据为信源，信源经RS 信道编码后交织，再依次进行MSK 调制、CIC 滤波，经中频载波频移和跳频调制后发送到信道.在信道中依次加入噪声和干扰.系统接收端的处理流程与发送过程相反:接收端先对接收到的信号进行解跳，而后依次进行中频解调、CIC 抽取滤波、MSK 解调后进行解交织，再经RS 解码得到发端信息.在接收端得到信息后要计算当前频点的误码率，并根据误码率自适应选择跳频频点.

设经过MSK 调制的基带信号为S(t)，信道中加入的高斯白噪声为N.则加入噪声后的信号为

中频标称频率为fc，干扰功率系数为J，干扰的频率偏移为Δf，则加入干扰后的信号为

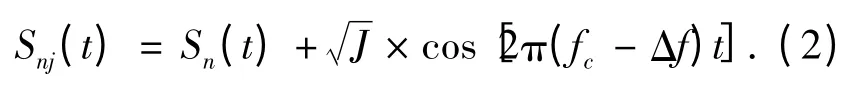
2 交织方法概述

2.1 问题描述

交织器一般可分为随机和确定性交织器两大类，是以一一映射的方式将输入符号的顺序重置，而解交织器将被交织器置乱的符号重新排成原始顺序.各种交织技术及多重交织技术已被民用及军用系统的各种标准广泛采纳和应用，其中最典型的是基于Turbo 信道编码的系统和WLAN 标准中［4，7，10］.如:并行Turbo 译码器结构结合交织技术应用于高速率系统中［11］;WLAN系统的IEEE802.11n 协议中的交织器硬件结构［12］;3GPP标准中的Turbo 交织是将输入比特流在矩阵中进行行内和行间交织得到新矩阵，再剪切后得到输出比特流;另有研究表明基于整数环模置换多项式的交织器性能比较好，二次置换多项式交织器实现最大扩展因子可进一步提高Turbo 交织的性能［13－14］.

衡量交织器性能的典型参数除不动点数目外，还有交织相关系数、交织延时、存储量.下面对各衡量参数进行简单说明.

1)交织相关系数.交织相关系数是用来衡量交织器性能的好坏.在交织矩阵的大小为M×N下，交织相关系数为

显然，相关系数ρ 越小越好.

(2)交织延时.交织延时是指任何1 个符号在它被插入到输出序列之前所经过的最大延迟时间.

(3)存储容量.存储容量是指交织器或解交织器交织矩阵的大小.一般来说交织阵的存储容量越大，相应的交织延时也越长，通信的实时性越差，但交织的效果也越好.因此需对通信实时性和交织效果进行折中.

2.2 行列交织方法

行列式的分组交织也称为块交织，分组长度为L=M×N，故又称之为(M，N)分组交织.行列交织的地址序列是按列写入按行读出，如图2 所示.行列交织分为A 型和B 型，两者写入方式相同，A 型读出顺序是从前往后按列读出，B 型是从后往前按列读出.

2.3 伪随机交织方法

伪随机交织方法的交织规则如下:对于长度为n 的信息序列，先标记每个比特位置，再生成相应n 个［0，1］之间的随机数，按产生的顺序排列成序列X，每个随机数对应于信息序列中相应位置的信息比特，再把X 中元素按一定规则重新排列得到新序列Y，并按Y 中元素的顺序读出相应的信息比特.Y 中元素的位置顺序便是伪随机交织的地址序列.对伪随机交织而言，每个长度为N的伪随机交织器共有N 种交织方式，体现了香农在有噪信道编码理论中的“随机特性”.

图2 行列交织方法的实现示意

从性能角度，在众多交织方法中，伪随交织方法性能最优.但伪随交织方法也有如下缺点:

1)在短帧交织下，采用伪随机交织器计算产生的随机数间存在一定相关性;

2)对每一组(帧)信息序列所用的交织器均不相同，具有一定随机性，而译码器要求对每帧数据有相应的解交织器对其解交织，所以在传输编码序列时，信道上还需传输交织器信息，加大了信道传输负载.若交织器信息出现错误，会使译码的误码增多.在最先提出的Turbo 码中C.Berrou 等使用的就是伪随机交织器.通过增加随机性，将混沌交织器和Dithered Relative Prime(DRP)交织器相结合，Turbo 码的误比特性能会有所提升［15］.

3 新型交织方法

在跳频通信系统中，采用交织的方法将Turbo编码符号均匀的分散在各个数据跳内，从而达到使单跳信息被删除的影响降低到最小的目的.本文提出的新型交织方法利用素数码及平方素数码的特性，产生素数码族作为交织的地址序列.与其他常用交织方法相比，具有实现简单、低延时以及占用存储资源少的特点.采用本文交织方法与不采用交织相比，在系统复杂度小幅增加前提下，显著提高了自适应跳频通信系统的抗干扰效果.

3.1 新型交织方法概述

本新型交织方法根据交织符号的个数选择合适的素数p 产生素数码矩阵，从而形成地址序列.信号序列先要变成信号矩阵并根据产生的素数码矩阵调整信号矩阵，而后依照素数码矩阵对信号矩阵进行交织.接收端的解交织过程与交织相反.接收到的信号先变换为矩阵，再依据与发端相同的素数码矩阵进行解交织，而后根据素数码矩阵对解交织后的矩阵进行调整，变换为序列后便可进行信道解码.

3.2 素数码及平方素数码的产生

新型交织方法的地址序列基于素数序列族.素数序列族起源于E.L.Titlebaum 提出的线性同余跳频码(Linear Congruence Code 码)［16］.

1)素数码的产生.素数码构造方法是利用模p 乘法表(p 为素数).设p 为素数，由su(j)=uj mod p 定义的长度为L=p 的序列

将素数码为有限基域乘法结果的构造思想进一步延伸到有限扩域GF(p2)上，即研究基于有限域GF(p2)以形为x2－y－1(y 为素数p 的二次非剩余)的二次既约多项式为模的域乘法结果，构造出新的跳频序列族，因其序列长度为p2，因此命名为平方素数码.

2)平方素数码的产生.有限扩域GF(p2)乘法是由以GF(p)中元素为系数的n－1 次多项式以n 次既约多项式f(x)为模实现的［17］.平方素数码只考虑n=2 情况.由有限域理论，可以证明二次多项式f(x)=x2－y 为GF(p)上的二次既约多项式，其中，y 为素数p 的二次非剩余.

为实现素数码在GF(p2)上的扩展，以GF(p)中元素的二维向量来表示上述素数码中的各个参数，设(i，j)表示横轴序号l，(a，b)表示码字序号m，(k1，k0)表示纵轴序号k，这里l=ip+j，m=ap+b，k=k1p+k0.对应的多项式分别为:l(x)=ix +j，m(x)=ax +b，k(x)=k1x +k0，i，j，a，b，k1，k0∈GF(p)且(a，b)≠(0，0).根据以上约定，以f(x)=x2－y 为既约多项式，由下式实现GF(p2)域乘法:

其中:⊕表示模p 加，i，j，a，b ∈GF(p)，且(a，b)≠(0，0).(a，b)，(i，j)分别表示码字序号及时隙序号，对应序列表示为(aj ⊕bi，bj ⊕yai).

3.3 新型交织方法中地址序列的产生

控制自适应跳频系统信息符号交织的地址序列选择素数码，其具体实现规则为:有限域GF(p)上模p(p 为素数)乘法的生成表达式如下:

其中:k 表示纵轴序号;m 表示码字序号;l 表示横轴序号［18］.

素数码矩阵的具体构造过程如下:

1)设p 为素数;

2)将有限域GF(p)上的元素以升阶或降阶列出，如:G={0，1，2，…，p－1}.

3)将G 中各元素同乘某一非零域元素u，1 ≤u ≤p－1，得到1 个非重复序列Su，

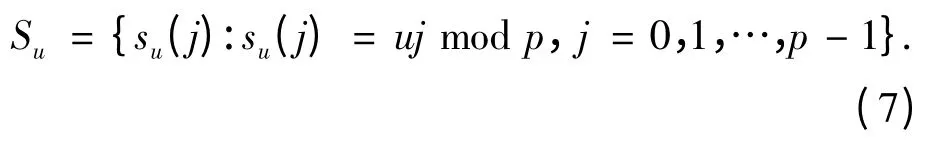
4)通过乘以不同的非零域元，共可得到p－1 个长度为p 的非重复序列.以p=13 为例，按上式构造素数码，得到如表1 所示的素数码矩阵.

表1 p=13 时的素数码矩阵

新型交织方法的交织地址序列采用素数码矩阵中的非零值和非自然排序序列，即上表1 中的粗体数字，作为新型交织方法中的地址序列.

3.4 新型交织方法的实现

信号序列要变换成M×N 的矩阵，而后根据信号序列的矩阵大小产生维度合适的素数码矩阵，依照修正后的素数码族矩阵对信号序列进行交织，通常为了节省空间可以在形成矩阵某行后进行交织，交织形式可为行或列交织.素数码交织后的信号矩阵再变为信号序列就完成了交织;接收端在接收到信号序列后先要将信号序列变换成与发送端相同维度的M×N 矩阵，而后用与发送端严格同步的素数码矩阵对此信号矩阵进行解交织，解交织后的信号矩阵变换为信号序列后就可进行后续处理，如图3 所示.

本文提出的交织方法与行、列交织相比实现简单而灵活.在交织过程中根据每组信息符号个数确定素数p 的值，只要保证素数码矩阵的元素大于信息符号的个数即可.

图3 新型交织方法的系统流程

4 各种交织方法性能比较与仿真分析

基于上述新型交织方法的描述，用matlab 软件搭建的“基于交织的自适应跳频系统”对其进行Monte Carlo 仿真，并与其他交织方法进行性能比较.仿真的系统参数如下:对基带信号进行MSK 调制，基带信息速率为50 kbps，基带信号带宽为60 kHz;信道噪声为高斯白噪声;单音干扰相对于中频的偏移为400 kHz，干扰的功率系数为0.011;跳频速率为5 kbps;中频载波频率范围为从600 kHz 到3 750 kHz，相邻载波频率间隔为50 kHz;备选频率范围为从3 800 kHz 到5 350 kHz，相邻备选载波频率间隔也为50 kHz;共有64 个载波频点及32 个备用载波频点供随机选择;SNR 的范围为5～30 dB;并假设接收端在跳频图案获得理想同步情况下后进行解交织.仿真结果如图4 所示.

图4 新型交织方法与其他交织方法的性能比较

图4 中的误码率数值都是经过30 次，每次106个仿真数据进行仿真并平均得到的，这里仿真数据量的选取原则按照Eb/N0为30 dB，结合置信度为99% 误码率的公式计算得出，即仿真数据总量≥100/Pe，等于106.从图4可见，在Eb/N0小于15 dB 时，各种交织方法的误比特率性能十分接近;在Eb/N0从15 dB 到30 dB 变化时，无交织时的误码率曲线下降趋势相对比较缓慢，性能最差;行列交织的误码率曲线较平滑下降，性能稍好;素数码和平方素数码交织的误码率性能均好于行列交织，两条曲线有交叠，表明二者性能相当;伪随机交织性能最好，但随SNR 增大，曲线下降速度并没有素数码和平方素数码误码率曲线下降的快，这表明素数码族交织在信噪比较高时，性能逼近伪随机交织.由此可看出本文提出的交织方法对单音干扰有较好的抑制效果，其抑制干扰的性能要好于普通的行列交织方法，而与伪随机交织方法的性能相差不多.进一步的，基于交织方法4 个主要性能参数，对本仿真平台使用各种交织方法进行性能评估.仿真过程中，对于不同交织方法均采用输入相同点数的数据进行交织.对于行列交织和伪随机交织，它们存储的是整个交织表，且在行列交织中按行输入按列读出第1 个点和最后1 个点的位置保持不变.经过对各种交织方法的交织参数的仿真与计算，得出各种交织器的性能参数如表2 所示.

表2 几种交织方法性能参数的比较

由表2 可以看出素数码族交织在各方面都要优于行列交织，尤其在存储量上要明显好于行列交织.而本文提出的新型交织方法和伪随机交织相比，在交织延时和存储量上也占有一定的优势，在存储量上的优势尤为明显.素数码交织的存储量优势，体现在数据以行或列进行交织，地址序列每计算出一行地址值就可进行这一行的交织，不需要多余存储其他行的数据，因此存储量大大降低到每行元素的个数(本仿真中行元素为40).

综合表2 可以看出素数码交织和平方素数码交织在相关系数、交织延时和存储量上和常规的行列交织和伪随机交织相比有较大优势.

5 结论

本文给出的新型交织方法使用素数码族生成交织地址序列，具有相关系数小、低延时、存储量需求小且实现灵活，不用刻意考虑矩阵维数的特点.能够改善系统出现连串错误时超出纠错编码纠错能力的抗误码性能.仿真结果表明新型交织方法使自适应跳频系统对单音干扰有较好的抑制效果，其抑制干扰的性能与平方素数码相当，好于普通的行列交织方法，而仅仅略低于随机交织的性能.因此，新型交织方法使得自适应跳频通信系统具有较好的抗干扰性能，具有广泛的应用前景.

［1］LEE S H，LEE Y H.Adaptive frequency hopping for bluetooth robust to WLAN interference［J］.IEEE Communications Letters，2009，9(13):628－630.

［2］CORREIA A M C，RODRIGUES A C B.Adaptive frequency-hopping for TDMA/CDMA［C］//48thIEEE Vehicular Technology Conference.Piscataway:IEEE.1998，3:2212－2216.

［3］HSU A C，WEI D S L，JAY KUO C C.Enhanced adaptive frequency hopping for wireless personal area networks in a coexistence environment［C］//IEEE Conference on Global Telecommunications.Piscataway:IEEE.2007:668－672.

［4］KABASHI A H，O＇FARRELL T.Low complexity CMCCDM based wireless LAN with different interleaving approaches［C］//IEEE 19th International Symposium on Personal，Indoor and Mobile Radio Communications.Piscataway:IEEE.2008:1－5.

［5］黄建平.基于周期无碰撞区跳频序列的自适应跳频系统研究［D］.成都:西南交通大学，2009.

［6］DING C S，YIN J X.Sets of optimal frequency-hopping sequences［J］.IEEE Transactions on Information Theory，2008，8(54):3741－3745.

［7］SIAUD I，ULMER-OLL A M.Advanced dynamic binary interleaving codes for UWB-OFDM WPAN systems［C］//IEEE Conference on GLOBECOM Workshops.Piscataway:IEEE，2009:1－6.

［8］ANDERSSON G.LPI performance of an adaptive frequency-hopping system in an HF interference environment［C］//IEEE 4th International Symposium on Spread Spectrum Techniques and Applications.Piscataway:IEEE，1996，2:903－907.

［9］Liu Y S.Bit-interleaving in fast FH/SSMA systems with M-FSK modulation［J］.IEEE Transactions on Wireless Communications，2007，6(9):3154－3158.

［10］JASPAR X，VANDENDORPE L.Impact of variable length codes on the interleaving gain of turbo systems:the concept of bounded spectrum.IEEE Transactions on Communications，2011，59(7):1796－1806.

［11］TARABLE A，BENEDETTO S.Mapping interleaving laws to parallel turbo decoder architectures［J］.IEEE Communications Letters，2004，8(3):162－164.

［12］张振东，吴斌，朱勇旭，等.IEEE802.11n 无线局域网中的多模交织研究与实现［J］.电子科技大学学报，2011，40(3):383－387.

［13］SUN J，TAKESHITA O Y.Interleavers for turbo codes using permutation polynomials over integer rings［J］.IEEE Transactions on Information theory，2005，51(1):101－119.

［14］TAKESHITA O Y.A new metric for permutation polynomial interleavers［C］//ISIT.Seattle:［s.n.］，2006:1983－1987.

［15］张卫党，康惠平，高辉.Turbo 码中一种基于混沌映射的DRP 交织器设计［J］.郑州大学学报(工学版)，2011，32(5):73－76.

［16］TITLEBAUM E L.Time-frequency hop signals—part I:coding based upon the theory of linear congruences［J］.IEEE Trans，1981，AES-17(4):490－493.

［17］LIDL R，NIEDERREITER H.Finite fields ［M］.London:Addision-Wesley Publishing Company，1983.

［18］梅文华.跳频通信［M］.北京:国防工业出版社，2005.