黄土高原北部水蚀风蚀交错区产流条件及径流系数
2013-09-14卢龙彬黄金柏
卢龙彬,付 强,黄金柏
(东北农业大学 水利与建筑学院,哈尔滨150030)
降雨径流在整个流域系统中是最为活跃的水文因子,是流域水循环的基本环节,研究降雨径流过程有助于更好地开发利用流域水资源[1]。对于季节性水资源缺乏问题相对突出的黄土高原北部水蚀风蚀交错区而言,如何实现对可利用水资源的准确评估已成为一个亟待解决的课题[2]。到目前为止,对流域产流的研究较多,如高军侠等[3]利用人工模拟降雨试验,根据水力学理论,统计分析了黄土高原坡面超渗径流特征,指出黄土高原坡面产流以超渗产流为主;周宏飞等[4]认为,在下垫面条件一定时,降雨能否产生径流,很大程度上取决于降雨历时和降雨强度;李慧敏等[5]指出径流量的大小在很大程度上取决于降雨因素。总结降雨径流数值模型的有关研究可知,迄今为止的分布式流域降雨—径流过程的数值模型,大多是针对某一选定的流域或规模较小的试验区,普遍存在通用性不强的特点,很难在不同地区中小流域尺度之间推广应用[6]。针对黄土高原北部水蚀风蚀交错区,地表水资源的研究相对较少[7-8],鉴于此,本研究选取黄土高原北部六道沟流域为研究区,基于对观测水文数据的综合分析,揭示研究区的产流机制。基于运动波理论结合GIS技术构建适用于研究流域的降雨—径流数值模型,通过对降雨—径流过程数值计算结果的分析,推求研究区的径流系数。研究结果可为黄土高原北部中小尺度流域地表径流的准确推求提供实用的计算方法,并期待为该地区地表水资源的深入研究以及流域数字化建设提供基础数据。
1 材料与方法
1.1 研究区概况
六道沟流域位于陕西神木县以西14 k m处(北纬35°20′—40°10′,东经103°33′—113°53′),地处黄土高原北部的水蚀风蚀交错区。多年平均降水量为437 mm,降雨季节性分布很不均匀,70%以上的降雨集中在7—9月(图1),且多暴雨,年潜在蒸发量超过1 000 mm[9-10]。流域内地形非常复杂,沟道纵横交错,土地沙化严重。对土层进行实际调查发现:该区域的表层土厚度为10~20 c m,表层以下是厚度超过15 m的坚硬的黄土层,再下层是侏罗纪砂岩[11-12]。
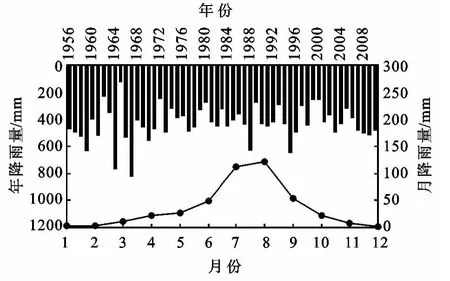
图1 研究区多年降雨量(1956-2009年)与降雨量月分布
1.2 水文观测
水文观测主要包括降雨、河道内径流、土壤水分等。因为六道沟流域内自然条件相似,为减少外界因素破坏,观测点选在人为因素干扰较少的流域上游。降雨的观测采用翻倒式自动计数雨量计(型号:7852 M-L10,尺寸 Φ165×240 H(mm)),每发生0.2 mm降雨记录数据1次。可利用Box Car Pro.4.3软件对观测得到的降雨数据在时间轴上用不同的时间间隔如3,5,10 min等进行分割,从而可以得到不同时间步长序列的雨量数据。由于只有在雨季集中降雨发生期间才产生地表径流,且流量受降雨强度的影响较大,所以采用精度较高的自动记数水位计(型号及制造商:KADEC21-MZPT (KONA System co.ltd)对地表径流进行观测,其观测精度为误差小于1 mm,观测的时间步长为5 min;为了使流量数据和降雨数据在时间步长上保持一致,以时间步长5 min对降雨数据进行分割,即文中所提及的雨强(平均降雨强度)为5 min降雨量的算术平均值。土壤水分的观测采用多探头感应式土壤水分计进行(制造商:Decagon Devices Inc,型号:EC-5),测量的指标为土壤的体积含水率,测量精度为误差小于3%。观测点位于地表径流观测断面两侧的坡面上(图2)[13]。

图2 地表径流及土壤水分观测示意图
2 结果与分析
2.1 长历时低强度降雨条件下的产流机制
图3所示为2008-06-15—2008-06-16降雨、观测断面土壤水分变化及地表径流产生的过程,本次降雨事件历时1 335 min,降雨量为86.2 mm,最大降雨强度为6.7×10-6m/s(2 mm/5 min)。由图3可知,降雨开始后5 c m处的土壤水分在某一时刻开始增加,而两侧坡面5 c m处的土壤水分含量开始增加的时间点不同;20 c m处的土壤水分含量开始增加的时刻滞后于5 c m处;50 c m处土壤水分含量在径流产生之前保持相对稳定。产流前,由于降雨强度低于表层土壤的不饱和渗透系数,加之表层土壤未达到饱和状态,所以不满足产流条件。当表层土壤(土壤水分观测深度:5 c m)达到饱和时,开始产流,产流时的降雨强度为2×10-6m/s(0.6 mm/5 min)。产流时,20 c m深处的土壤水分含量有了较明显的增加,而50 c m处的土壤水分含量依然保持相对稳定状态,此为长历时低强度降雨条件下的产流机制。
2.2 短历时高强度降雨条件下的产流机制
图4所示为观测断面2008-08-29降雨、土壤水分变化及地表径流产生的过程。此次降雨发生在当日午后14:00—15:00,平均降雨强度超过1.67×10-5m/s(5 mm/5 min)。由图4可知,降雨开始10 min后开始产流,此时降雨强度为1.4×10-5m/s(4.2 mm/5 min)。产流时,除观测断面右侧坡面5 c m处土壤水分略有增加外,其它各观测点土壤水分保持稳定状态。对随机选取的多次降雨—径流事件的分析表明:在短历时条件下,降雨强度达到0.52 mm/min(2.6 mm/5 min)时,表层土壤在不饱和时便可以产流,结合对图4所示降雨—径流事件的分析结果,可以得出试验流域在短历时高强度降雨条件下,表层土壤未达到饱和状态时的产流条件是降雨强度达到或超过0.52 mm/min(2.6 mm/5 min)。

图3 长历时低强度降雨条件下的产流事件

图4 短历时高强度降雨条件下的产流事件
2.3 降雨因子与径流系数的关系
2.3.1 平均降雨强度与径流系数的相关性 降雨强度、降雨历时和降雨量等降雨因子都是径流过程和径流量的影响因子[14-15],为了评价主要降雨因子对径流的影响,随机选取多次降雨—径流事件,其降雨历时、降雨量、平均雨强及径流系数如表1所示。因为试验流域所在地区只有在雨季集中降雨期间且满足产流条件时才能产生地表径流,所以本文所述的随机降雨—径流事件指在观测得到的降雨—径流事件中抽样选取的事件。其中既包含短历时的降雨事件又包含长历时降雨事件。根据表1中数据绘制平均降雨强度和径流系数的关系曲线如图5所示,由该图可知:平均降雨强度与径流系数之间存在着较高的正相关性(R2>0.87),即随着平均降雨强度的增加,径流系数呈增大的趋势。
2.3.2 降雨历时及降雨量与径流系数的关系 根据表1中数据绘制的降雨历时与径流系数、降雨量与径流系数的关系曲线分别如图6、图7所示,由图6、图7可知,降雨历时与径流系数之间没有显著的相关性,但存在轻微的反比例趋势,即随着单次降雨事件历时的增加,径流系数呈减小的趋势,但不明显。降雨量与径流系数之间亦不存在显著的相关性,二者之间也存在着轻微的反比趋势,即随着单次降雨事件降雨量的增加,径流系数有轻微减小的趋势。由以上分析可知,在平均降雨强度、降雨历时和降雨量3个降雨特征因子中,平均降雨强度是影响径流系数的主要因子,二者存在着较高的正相关性。
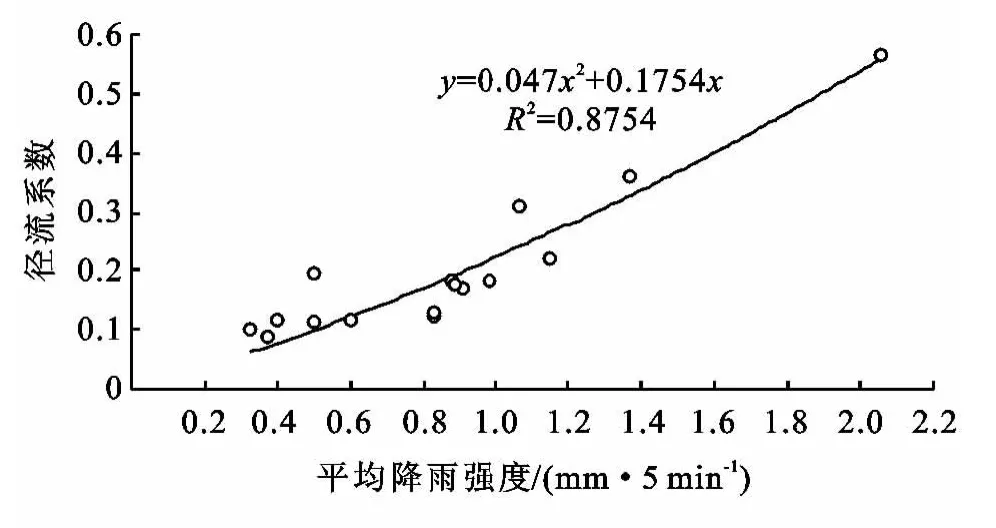
图5 平均降雨强度-径流系数关系曲线

图6 降雨历时-径流系数关系曲线

图7 降雨量-径流系数关系曲线
3 降雨-径流数值模型
3.1 模型构建
3.1.1 河网构建 利用 Arc GIS工具中的 Archydr ol gy和Arcview平台,对流域地形进行分析,包括基于DEM流域特征的提取,水系的提取、子流域的划分、流域边界线的提取、地形指数的计算、单元汇流路径长度的提取等[16-17]。依据空间上各沟道连接的相对位置关系将试验流域分割成若干个分布式小流域,从而可以通过各个小流域的空间结合来表达试验流域的整体。按最大坡度方向决定地表汇流方向[18]。拟河道网是在数字标高模型和水流方向线生成的基础上,利用Arcview生成的,按上述方法生成的地表径流观测点上游集水区(计算区域)的河网如图8所示。为了实现基于运动波理论建立的模型的径流计算,将流域以拟河道网为依据进行分布式分割,将流域划分成若干个分布式小流域。
3.1.2 水文地质模型 根据对试验流域土壤纵剖面实际调查的结果,基于研究区实际水文地质条件,构建水文地质模型如图9所示。模型由坡面区间和河道区间构成,坡面区间在纵断面由两层构成,河道区间在纵剖面上由一层构成。

图9 水文地质模型
3.1.3 算法建立
(1)连续方程式。图10所示为任意流域的单元体水收支示意图,对于地表径流,在计算时间步长Δt内以质量守恒定律(水收支平衡法)建立如下数学模型:

式中:b——单元体宽度(m);d x——流向上的单位长度(m);Δt——时 间 步 长 (s);r——降 雨量 (m/s);f1——第一层土壤平均渗透速度(m/s);A——地表径流的断面面积(m2);Q——流入量(m3/s);(Q+∂Q/∂x)——流出量(m3/s)。
因为A=b·h,Q=A·v[h为地表径流深度(m);v为流速(m/s)],其他因子同前,对方程式进行整理两边同时约去b,得

按照同样方法,可以推得第一层地下水的连续方程式为:

式中:λ——第一层的有效孔隙率;¯q——单宽流量(m2/s);¯h——水深(m);f1——第一层土壤平均渗透速度(m/s);f2——由第一层向第二层的渗透速度(m/s);E——蒸散发量(m/s);蒸散发量认为从第一层产生(土壤水分);t——时间(s);x——水流方向上的距离(m);用同样的方法,如果土壤在纵剖面上按照土壤性质(包括含水层)可分成多个层,则可以建立任意层的水流运动的连续方程式:

式中:i——层号;λi——第i层的有效孔隙率;¯qi——第i层单宽流量(m2/s);¯hi——第i层水深;fi——由第i-1层向第i层的渗透速度;fi+1——由第i层向第i+1层的渗透速度,降雨期间,因为植物的蒸散发可以忽略,同时,考虑到研究区的地表径流只有在雨季集中降雨发生期间才能产生,而且存在时间很短等特点,所以,采用一个损失系数评价降雨期间的蒸散发[19]。
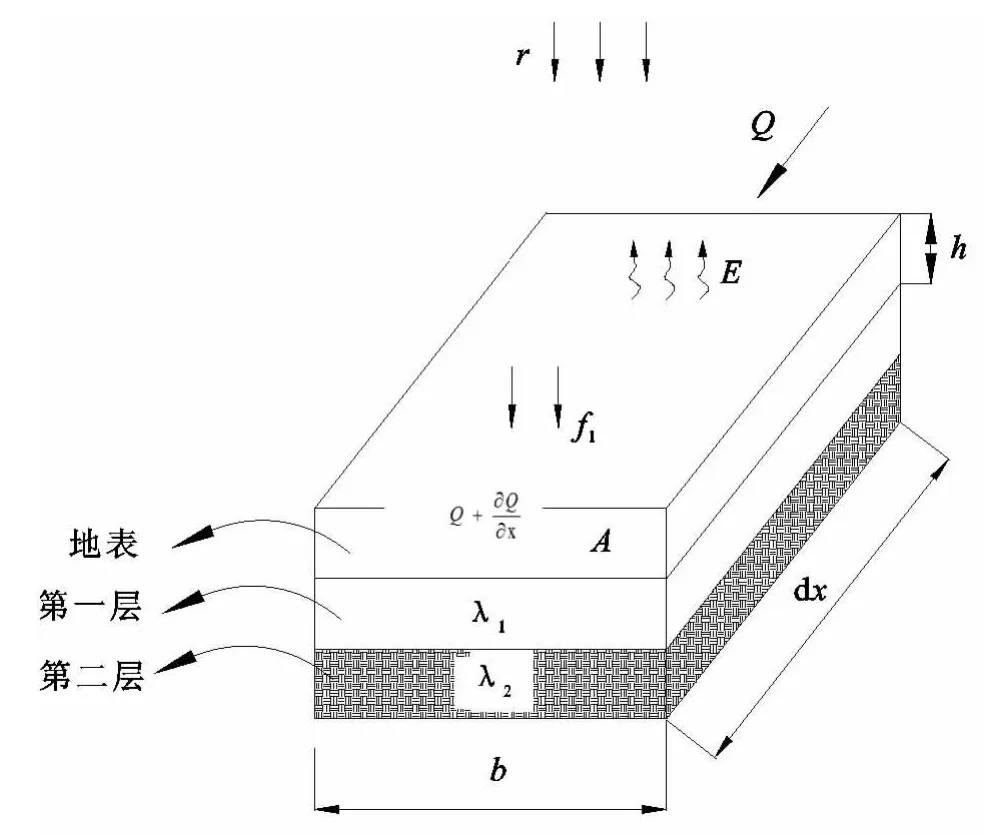
图10 流域单元体水收支示意图
(2)运动方程式。运动波理论是基于河道抵抗法则基础之上,水流基础方程式之一的运动方程式可以用等流的河道抵抗法则置换,即一维水流计算的运动方程式可以用平均流速公式来代替,因此,地表径流计算的运动方程式为曼宁平均流速公式:
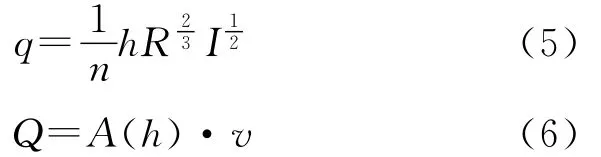
式中:h——水深(m);q——单宽流量(m2/s);n——曼宁粗度系数(s m-1/3);R——水力半径(m);I——水力坡降(计算时用河道坡度近似代替),其它因子与前述一致。地下水(渗透)连续方程式为:

3.1.4 差分计算 在时间上和空间上用有限差分法对地表流和渗透流连续方程式进行离散化,实现连续计算。因为数值计算要依赖于流域最末级子流域端部的边界条件和初始条件,所以采用后退差分法进行差分,差分公式如下:
地表流连续式的差分公式:

渗透流连续式的差分公式:

式中:n——计算的时间次序;i——水流方向上计算格子的编号;其它因子与前述相同[21]。
3.1.5 计算参数 计算所用主要参数如表2所示。参数由实地调查、水准测量、参考同一研究区的有关研究成果以及利用模型进行海量运算,对部分参数进行寻优等方法确定的。

表2 主要计算参数
3.2 数值模拟
(1)一次“降雨—径流”事件的数值模拟:以2008年9月23—24日观测的典型降雨和地表径流为例,数值模拟的结果如图11所示。误差分析结果表明,模拟结果与观测流量的误差小于3%。
(2)数次“降雨—径流”事件的数值模拟:以2004年8月11日至22日观测的降雨及产流结果为例,数值模拟结果如图12所示。误差分析结果表明,观测流量与模拟流量之间的误差均在误差判断基准允许范围之内(误差<3%)。

图11 一次降雨径流事件模拟(2008-09-23-24)

图12 数次降雨径流模拟结果(2004-08-11-22)
3.3 数值计算
利用降雨—径流数值模型和观测的降雨量,对试验流域2005—2009年(5 a)的降雨径流过程分别进行各年全年计算,结果如表3所示。

表3 2005-2009年降雨及年径流系数
由表3可知:2005—2009年的平均年降雨量为439 mm/a,与多年平均降雨量437 mm/a相近,5 a的年平均径流系数为0.11,与在同一区域用长期观测的方法而得到的结果几乎相等,可以近似地推得研究流域所在地区的年径流系数应该在0.10~0.15。基于以上结论可知:本研究所开发的地表径流计算模型效率较高,可以为该地流域提供一种较为精确的数值计算方法。
4 结论
本研究基于对观测水文数据的分析,揭示了研究区在长历时低强度降雨以及短历时高强度降雨条件下的产流机制;开发了适用于黄土高原北部水蚀风蚀交错区降雨—径流过程的数值计算模型,利用试验流域2005—2009年的降雨数据进行了计算并对结果进行了分析,得出的结论如下:
(1)试验流域在长历时低强度条件降雨条件下,产流的必要条件是表层土壤达到饱和且降雨强度达到或超过0.12 mm/min(0.6 mm/5 min);在短历时高强度降雨条件下,产流的条件是降雨强度达到或者超过0.52 mm/min(2.6 mm/5 min)。
(2)在平均降雨强度、降雨历时和降雨量3个降雨因子中,平均降雨强度是影响径流系数的主要因子,其与径流系数之间存在较好的正相关性;降雨历时和降雨量与降雨径流系数之间只存在着轻微的反比趋势。
(3)试验流域2005—2009年的年平均径流系数为0.11,根据2005—2009年的年平均降雨量与试验流域所在地区多年平均降雨量几乎相等的事实,近似地推得试验流域所在地区的多年径流系数为0.1~0.15。
(4)研究开发的分布式流域降雨—径流数值模型适用于试验流域所在地区的水文地质条件,因此可在同一地区中小尺度流域的降雨径流计算中推广应用。
[1] 孙颖娜,芮孝芳,付强,等.基于随机微分方程的流域产汇流模型[J].水利学报,2011,42(2):187-191.
[2] Hinokidani O,Huang J B,Yasuda H,et al.Annual water budget of a small basin in the norther n Loess Plateau in China[J].Journal of Arid Land Studies,2010,20(3):167-172.
[3] 高军侠,刘作新,党宏斌.黄土高原坡面模拟降雨超渗径流特征分析[J].土壤通报,2004,36(6):780-784.
[4] 周宏飞,王大庆,马健,等.天山山区草地覆被和雨强对产流和产沙的影响研究[J].水土保持通报,2009,29(5):26-29.
[5] 李慧敏,张建军,徐佳佳,等.黄土高原不同下垫面小流域径流特征[J].东北林业大学学报,2011,39(10):90-113.
[6] 芮孝芳,黄国如.分布式水文模型的现状与未来[J].水利水电科技进展,2004,24(2):55-58.
[7] Hinokidani O,Huang J B,Yasuda H,et al.Study on surface r unoff characteristics of a s mall ephemeral catchment in the norther n Loess Plateau,China[J].Jour nal of Arid Land Studies,2010,20(3):173-178.
[8] 王幼奇,樊军,邵明安,等.黄土高原水蚀风蚀交错区三种植被蒸散特征 [J].生态学报,2009,29(10):5384-5396.
[9] 唐克丽,侯庆春,王斌科,等.黄土高原水蚀风蚀交错带和神木试区的环境背景及整治方向[J].中国科学院水利部西北水土保持研究所集刊,1993,18:1-5.
[10] 王万忠,焦菊英,郝小品.黄土高原暴雨空间分布的不均匀性及点面关系[J].水科学进展,1999,10(2):165-169.
[11] 李免,李占斌,刘普灵,等.黄土高原水蚀风蚀交错带土壤侵蚀坡向分异特征[J].水土保持学报,2004,18(1):63-65.
[12] Wang Q X,Takahashi H.A land surface water deficit model for an arid and semiarid region:i mpact of desertification on the water deficit status in the Loess Plateau,China[J].Journal of Cli mate,1999,12(1):244-257.
[13] 王云强,张兴昌,从伟,等.黄土区不同土地利用方式坡面土壤含水率的空间变异研究[J].农业工程学报,2005,19(1):65-71.
[14] 王贵作,任立良.基于栅格垂向混合产流机制的分布式水文模型[J].河海大学学报:自然科学版,2009,37(4):386-390.
[15] 焦菊英,王万忠,郝小品.黄土高原不同类型暴雨的降水侵蚀特征[J].干旱区资源与环境,1999,13(1):34-42.
[16] Huang J B,Hinokidani O,Yasuda H,et al.Study on characteristics of the surface flow of the upstream region in Loess Plateau[J].Annual Jour nal of Hydraulic Engineering,JSCE,2008,52:1-6.
[17] 任立良,刘新仁.基于数字流域的水文过程模拟研究[J].自然灾害学报,2001,9(4):45-52.
[18] 李忠武,蔡强国,曾光明,等.基于GIS的黄土丘陵沟壑区土壤水分模型研究[J].水利学报,2004(3):123-128.
[19] 黄金柏,桧谷治,梶川勇树,等.分步型流域“降雨—流出”过程数值模拟方法的研究[J].水土保持学报,2008,22(4):52-55.
[20] Kobayashi K,Takara K,Tachikawa Y.Parameter estimation of a distributed rainfall-runoff model by a levenber g-marquardt opti mization algorith m[J].Annual Jour nal of Hydraulic Engineering,JSCE,2007,51:409-414.
[21] 汪志荣,沈晋,王文焰,等.黄土区波涌畦灌条件下地表水流运动实验与数值模拟[J].农业工程学报,1994,10(1):36-43.
