基于禁忌粒子群算法的混流装配线排序研究*

翁耀炜，鲁建厦，邓 伟

（浙江工业大学 工业工程研究所，浙江 杭州 310014）

0 引 言

混流装配线可以在基本不改变生产组织方式的前提下，同时生产出多种不同型号、不同数量的产品，它是应对大规模定制生产的一种有效组织方式[1]。目前，我国家电、汽车生产行业大量采用了混流装配方式，装配线上合理的投产顺序能有效提高装配线的生产效率、降低生产周期和充分利用生产资源，因此解决混流装配线的排序问题是混流装配线能否高效运作的关键。

在求解混流装配线的排序问题上，通过智能算法求解是目前的研究重点。目前，常用的智能算法有遗传算法、粒子群算法（PSO）、蚁群算法等。郑永前、王永生等[2]通过免疫粒子群算法求解最小化超载时间与空闲时间的费用的混流装配线排序模型，但算法结果一般，且没有考虑其他影响装配线效率的因素；刘炜琪、刘琼等[3]通过混合粒子群算法求解以最小化超载时间、最小化调整时间、最小化产品变化率为优化目标的混流装配线排序模型，取得一定的效果，但忽略了所优化的多目标间的冲突和竞争；王炳刚、饶运清等[4]和苏平、于兆勤[5]通过混合遗传算法对零部件消耗均匀和最短生产循环周期对混流装配线排序问题进行优化；董巧英、阚树林等[6]通过改进离散微粒群算法对最小超载、空闲和调整时间的费用最低的混流装配线排序问题进行优化；薛琴微、兰秀菊等[7]通过小生境蚁群算法求解以传送带中断时间最短为目标的混流装配线优化模型。

与其他算法相比，粒子群算法在求解过程中，微粒只需要在解空间内追随最优的微粒进行搜索，并用公式来更新自己的速度及位置，不需要进行交叉和变异等操作，具有原理简单、计算方便、全局搜索能力强等优点。在连续空间的实值型处理上已经表现出优良的性能，但其不能直接进行离散空间问题的求解，且容易陷入局部最优点，禁忌搜索算法（TS，Tabu Search 或Taboo Search）[8]具有很强的局部搜索能力，可以有效避免陷入局部最优。

因此，本研究通过建立基于PSO 算法和禁忌搜索算法的模型求解混流装配线排序问题。

1 混流装配线排序数学模型建立

1.1 混流装配线排序问题描述

由于混流装配线的类型各不相同，目前学术界主要研究的是由传送带（链）连接的封闭作业域混流装配线。在这类装配线中，当某工作站未能完成产品的加工时，往往假设由线外的员工及时完成，但在实际生产中往往不能达到这个要求，而且一般家电、汽车的总装配线通常采用开放式的作业域。因此，为更加贴近实际生产要求，本研究对开发式作业域的混流装配线排序问题进行了研究。

开放式作业域的混流装配线排序模型可以描述为：混流装配线由传送带（链）连接N 个工位，传送带（链）以恒定速率VC移动，每个装配工位长度为Li，工位是开放的，装配线上的工人在装配时需要随着装配输送链的移动而移动，当工人不能在自身的工位内完成加工时，可以在不影响其他工位加工的情况下进入下游加工，同时也可以进入上游工位进行加工。假设：①工件的投产间隔时间固定，以间隔时间λ进行投产；②忽略工人的行走时间；③两个工位之间没有缓冲区。

有M 种产品需要在装配线上装配，每个品种的需求量为D1,D2,D3,…,DM，则总需求量为排序采用最小生产循环（MPS，Minimum Part Set）模式，即整个生产顺序由若干个MPS 构成，MPS 由各产品需求量比例形成最小生产序列，如每种产品的需求量为dm（m=1,2,3,…,M），h 为dm 的最大公约数，则每种产品在最小生产循环中的数量为dm/h，那么这个MPS可以表示为d1/h,d2/h,…dM/h。因此，只要对这个MPS进行排序，将最后排序的结果循环进行h 次，就可以得到整个装配产品的投产顺序。

1.2 混流装配线优化目标描述

针对排序问题采用不同的优化目标，排序结果会有很大差异。为提高装配线上工人和设备的利用率并缩短总装配时间，本研究选择以最小化超载时间和平顺化零部件消耗为优化目标。

1.2.1 最小化超载时间

在混流装配过程中，当工人在规定工位区域内没能完成装配任务，则剩余装配任务的标准工时为超载时间。Sarker 等[9]考虑了不完全开放式作业域的混流装配线模型，在此基础上扩展了其模型，建立了开放式作业域的混流装配线，该目标模型表示为：

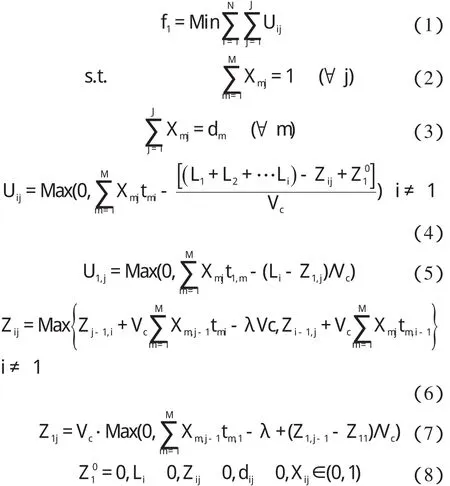
式中：J—一个MPS 的投产序列，j—序列中的某一顺序的产品，Uij—投产序列中第 j 个产品在工位i 上的超载时间，Zi,j—投产序列中第 j 个产品在工位i 上的起始装配位置，Zi0—工位i 的起始装配位置，L—工位的长度，Vc—传送带（链）的传送速度，λ—装配线上产品的投产间隔时间—序列中第 j 个产品在第i 个工位上的加工时间序列中第 j个产品所属的产品类型。

由于第一个工位属于封闭式的作业域，研究者需要另外计算，计算公式为式（5，7）。

1.2.2 平顺化零部件消耗

混流装配线上不同的产品需要的零部件不尽相同，因此平顺化零部件消耗是指将装配线上的不同产品所需零部件的消耗处于一个平稳的状态。

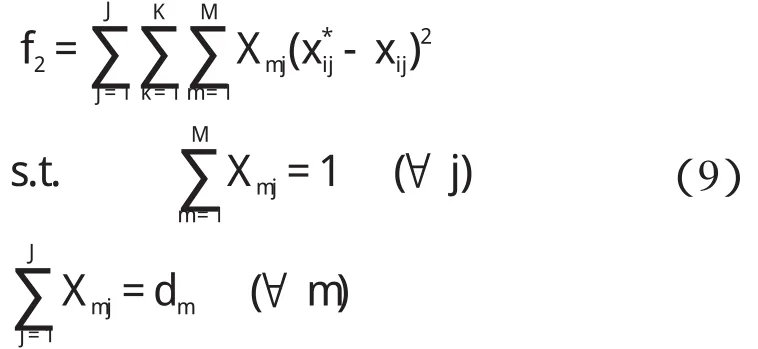
式中：f2—平顺化零部件消耗；x*ij—在一个MPS 中，装配前 j 个产品消耗第k 种零部件数量的期望值，J；Rk—在一个MPS 中装配所有产品消耗的第k 种零部件的数量；xij—在一个MPS 中，装配前 j个产品实际消耗的第k 种零部件数量—实际装配第m 种产品时所消耗的第k 种零部件的数量。

优化模型中采用了最小化超载时间与平顺化零部件消耗两个目标，是多目标优化问题。为求解多目标优化问题，本研究采用加权系数法。尽管该方法有其固有缺点，但考虑到它具有简单易行和求解速度快等特点，并且生产中需要的是可以接受的近优解，仍在实际运用中得到了大量的应用。因此，优化目标表示为：

式中：ω1,ω2—超载时间 f1和平顺化零部件消耗 f2在多目标优化问题中的重要程度的权重系数。

2 模型求解算法设计

2.1 标准PSO 模型

粒子群优化算法是一种进化计算技术算法，由Eberhart 和Kennedy 提出。在该算法中，种群中的每一个体被称为微粒，微粒在搜索空间中以一定的速度飞行，并根据它本身的飞行经历以及同伴的飞行经历进行动态调整。在每一次的迭代中，微粒通过跟踪两个最优解来更新自己，第一个是自身所找到的最优解，即个体极值 pbest，记为 Pi(t)=(pi,1(t),pi,2(t),…,pi,d(t))，式中：i—粒子数，d—问题维数；另一个是整个种群所找到的最优解gbest，记为Pg，微粒的更新速度和位置为：

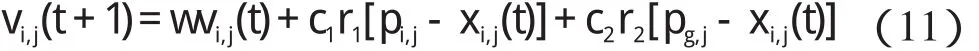
式中：c1,c2—学习因子；r1,r2—（0，1）之间的随机数；i—粒子数；j—问题某一维数；w—惯性权因子。

标准PSO 算法的流程如图1 所示。

图1 标准粒子群算法流程

在算法的初期，由于个体最优值pbest和全局最优值gbest在不断变化，算法全局搜索能力强。但是在算法的中后期，由于pbest和g best 变化不大，同时由于微粒具有“趋同性”，微粒速度将越来越小，最终使得大部分微粒速度接近或等于0，微粒位置得不到更新，有可能使算法陷入局部最优。禁忌搜索算法是一种全局性的邻域搜索算法。TS 在进行搜索时，它模拟人类大脑具有记忆功能的特点，对某些状态进行记忆，同时采用相对应的禁忌规则，使算法能够有效地避免循环搜索，提高算法的效率，并且算法采用“藐视准则”来特赦某些具有优良状态的解，避免丢弃导致由于禁忌规则的约束使一些状态良好的解被遗留，进而既提高了有效性又保证了算法执行中种群的多样化，最终实现了全局优化。

2.2 禁忌粒子群算法设计

由于PSO 算法的缺陷，本研究在标准PSO 中引入两种策略进行改进：引入禁忌搜索算法，通过TS 算法搜索每次迭代群体中的最优解，由于TS 算法的特点，使劣解也可以更新pbest，有利于改善算法的全局搜索性能；随机权重法，将权重w 设置为随机时，有可能加速算法的收敛速度，当算法初期找不到最好点时，由于w 的线性递减可能导致算法最终不能收敛到全局最优点，而随机权重可以克服这种局限。算法的关键及细节设计如下：

2.2.1 编码与解码方式

由于传统的基于产品表示的编码方式并不适用于PSO 算法的微粒进化方式，本研究需要新的解码和编码方式。假设一个MPS 中有1 个A 产品，2 个B 产品，3 个C 产品，则用数字1 代表A 产品，2 和3 代表B 产品，4、5 和6 代表C 产品，然后引入Bean[8]提出的随机数表示法进行编码，解码则采用映射规则依次升序解码。

2.2.2 惯性权重更新方式

将标准PSO 算法中设定w 为服从某种分布的随机数，可以从两方面克服由于w 的线性递减的不足。首先，在算法初期，随机w 可以产品相对较小的w 值，加快算法的收敛速度；其次，如果算法初期找不到最优解，随着w 的递减可能使算法最终收敛到局部最优点，随机w 可以克服这种局限性。

w 的随机更新计算公式为：

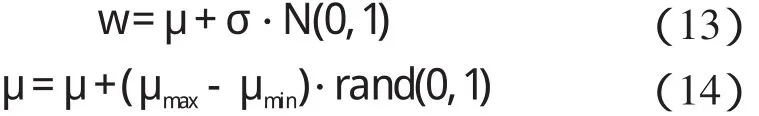
式中：N(0,1)—标准正态分布；rand(0,1)—0～1 之间的随机数；μmax，μmin—随机权重平均值的最大值和最小值；σ—随机权重的方差，由算法给定。

2.2.3 最优微粒的更新方式

在算法的每次迭代过程中都会得到一个gbest值，若经过g 次迭代后，g best 的值保持不变，则使用禁忌搜索算法进行邻域解的搜索，由于禁忌搜索可以接受劣解，提高了跳出局部最优解的能力。由于禁忌搜索采用邻域搜索方式，需要重新解码、编码。在禁忌搜索算法中候选解、禁忌表长度、禁忌对象、藐视准则是影响算法性能的主要因素。根据优化模型的优化问题和编码方式，禁忌表长度则根据经验设置为0.6 l（l 为候选解个数），候选解从邻域中选择若干目标值最佳的粒子入选，禁忌对象采用目标值的变化，藐视准则设置为根据适应度值的大小。最优微粒的TS 算法更新方式如图2 所示。

基于上述思想，禁忌粒子群算法的算法流程如下：

（1）随机初始化种群中各微粒的位置和速度；

（2）评价每个微粒的适应度，将当前各微粒的位置和适应度存储在各微粒的pbest中；将所有 p best 中最优个体的位置和适应度值存储在gbest中；

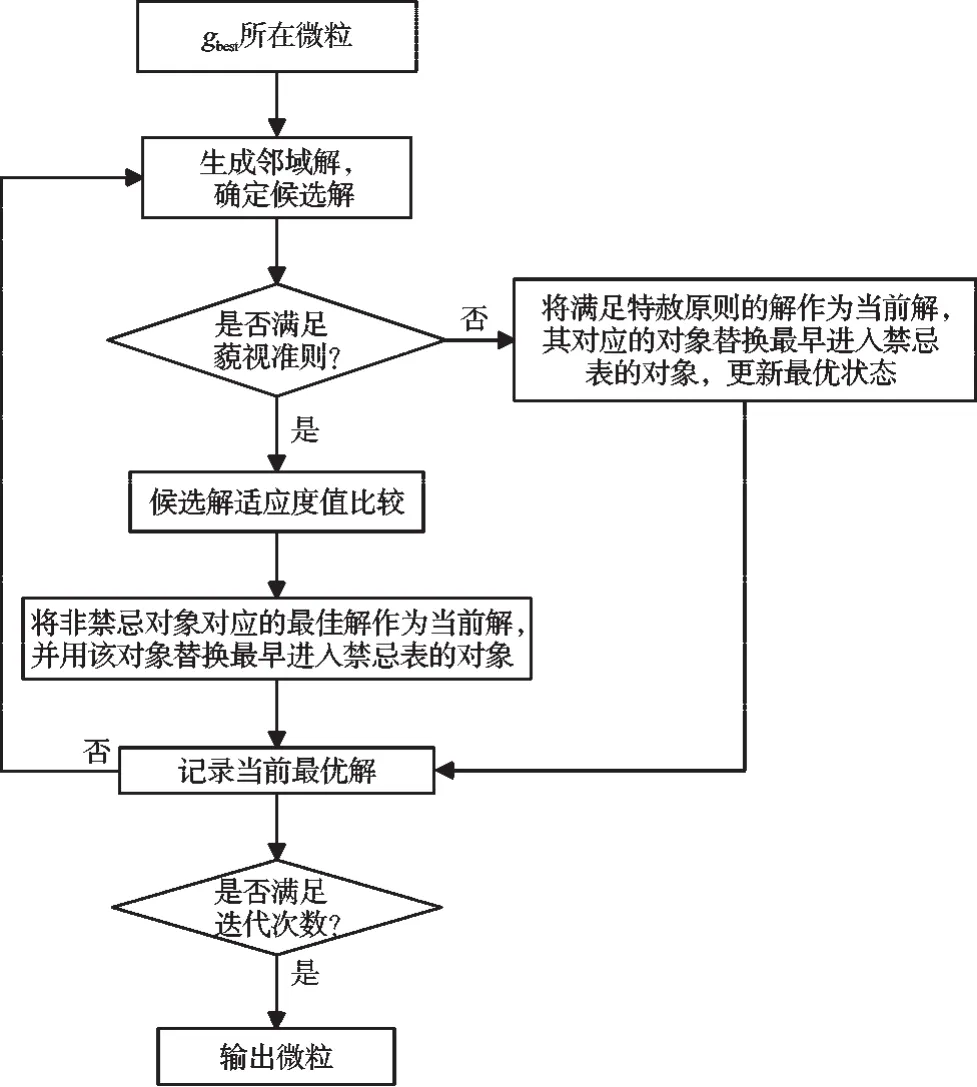
图2 微粒的TS 算法更新方式

（3）通过公式（11，12）更新微粒的速度和位移；

（4）对每个微粒，将其适应度值与其经历的最好位置作比较，如果较好，则将其作为当前的最好位置，并同时更新gbest；

（5）解码并重新编码对群体中的最佳微粒执行禁忌搜索，并更新其 pbest及群体的gbest；

（6）通过公式（13，14）更新权重值；

（7）若满足迭代次数，停止搜索，输出结果，否则返回步骤（2）。

3 实例研究

某冰箱装配企业某条总装线采用混流方式进行生产，该装配线共6 个工作站，混合装配4 种产品，计划日产量分别为120 台A 产品、40 台B 产品、60 台C 产品和40 台D 产品。那么日产的MPS 为6A，2B，3C，2D，共13 个产品。

各产品在各工作站上的装配时间以及工位长度如表1 所示；各个不同产品装配所需零部件如表2 所示。

GA 是目前求解混流装配线排序问题的常见方法[11-14]。因此，为了验证算法的优越性，本研究通过禁忌粒子群算法和GA 算法对案例进行优化。GA 算法参数：编码方式采用基于产品的编码方式，染色体选择策略为轮盘赌，迭代次数为100，种群数量20，交叉算子为单点交叉再进行编码修正，交叉概率为0.9，变异概率为0.09。禁忌粒子群算法参数：学习因子 c1=c2=2，μmax=0.8，μmin=0.8，σ=0.2，初始粒子种群数量为50个，迭代次数为500。装配线的运行参数为：Vc取10 mm/s，λ 取50 s，两个目标函数的权重w1，w2分别取0.5 和0.5。各个算法都运行10 次，取最优值。

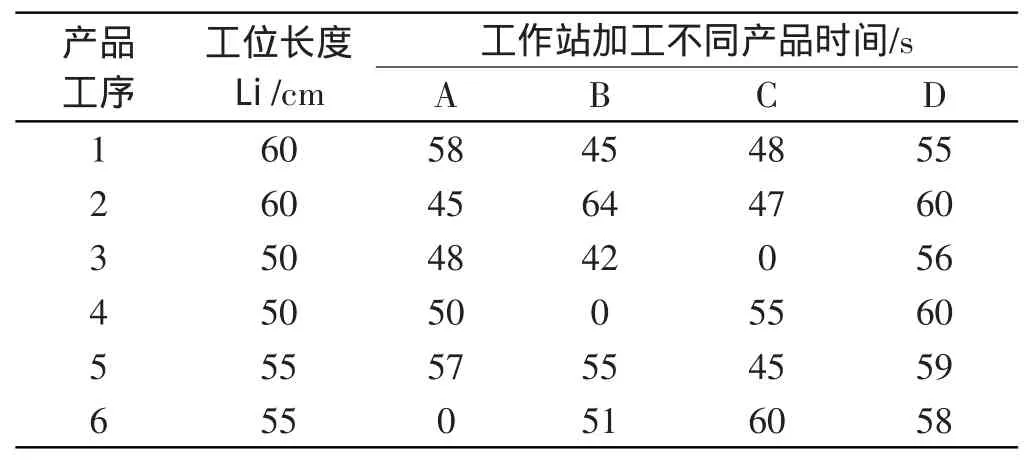
表1 工位装配产品时间及工位长度

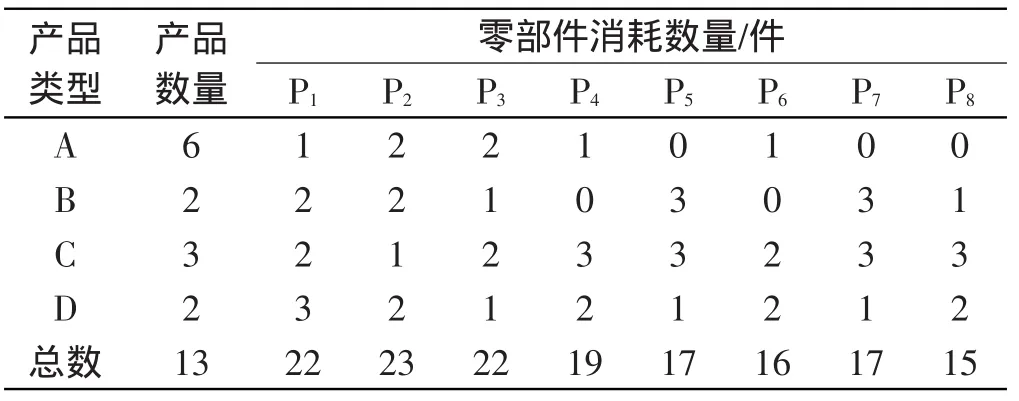
表2 各种产品所需零部件数量

两种算法的优化结果如表3 所示。禁忌粒子群算法的收敛图如图3 所示。

表3 案例优化结果及对比

图3 禁忌粒子群算法收敛图

由表3 和图3 可知，禁忌粒子群算法在计算结果上优于GA 算法，同时拥有很好的收敛速度。这是因为禁忌粒子群算法结合了粒子群算法全局搜索的能力以及和TS 算法在邻域搜索能力较强的特点以及随机权重更新方式，加强了算法的全局和邻域搜索的平衡能力，并且粒子群的快速收敛能力为禁忌搜索算法对提供了较好的初始解。

4 结束语

为了更好地解决开放式作业域的混流装配线排序问题，本研究探索了一种新的粒子群算法。针对开放式混流装配线，笔者建立了以最小化超载时间与平顺化零部件为优化目标的混流装配线排序数学模型；为求解该排序模型，给出了提高邻域搜索能力和跳出局部最优的解决方法，给出了平衡全局搜索和局部搜索的平衡方法，给出了禁忌粒子群算法流程；通过比较算例结果，本研究设计的禁忌粒子群算法在求解混流装配线排序问题优于遗传算法，验证了该算法的有效性。但由于禁忌粒子群算法还是对单目标优化问题的求解，且没有对算法中的相关参数的设定进行灵敏度的分析，还存在禁忌粒子群算法在多目标优化问题上的适用性问题和对算法参数研究不足的问题，有待于进一步研究。

（References）：

[1]邵新宇，饶运清.制造系统运行优化理论与方法[M].北京：科学出版社，2010：91-93.

[2]郑永前，王永生.免疫粒子群算法在混流装配线排序中的应用[J].工业工程与管理，2011，16（4）：16-20.

[3]刘炜琪，刘 琼，张超勇，等.基于混合粒子群算法求解多目标混流装配线排序[J].计算机集成制造系统，2011，17（12）：2590-2598.

[4]王炳刚，饶运清，邵新宇，等.基于多目标遗传算法的混流加工/装配系统排序问题研究[J].中国机械工程，2009，20（12）：1434-1438.

[5]苏 平，于兆勤.基于混合遗传算法的混合装配线排序问题 研 究[J].计 算 机 集 成 制 造 系 统 ，2008，14（5）：1001-1007.

[6]董巧英，阚树林，桂元坤，等.基于改进离散微粒群优化算法的混流装配线多目标排序[J].系统仿真学报，2009，21（22）：7103-7108.

[7]薛琴微，兰秀菊，陈呈频.基于蚁群算法的混流装配线排序研究[J].轻工机械，2010，28（5）：107-112.

[8]GLOVER FW.tabu search[Z].Springer，1997.

[9]SARKER B R P H.Designing a mixed-model，open-sta⁃tion assembly line using mixed-integer programming[J].The Journal of the Operational Research Society，2001，52（5）：545-558.

[10]BEAN J C.Genctic Algorithms and Random Keys for Se⁃qucncing and Optimization[J].ORSA Journal on Com⁃puting（S0899-1499），1994，6（2）：154-160.

[11]鞠全勇，朱剑英.基于混合遗传算法的动态车间调度系统的研究[J].中国机械工程，2007，18（1）：40-43.

[12]LEU Y，MATHESON L A，REES L P.Sequencing mixed-model assembly lines with genetic algorithms[J].Computers&；Industrial Engineering，1996，30（4）：1027-1036.

[13]苑明海，白 颖，李东波.可重构装配线多目标优化调度研究[J].中国机械工程，2008，19（16）：1898-1903.

[14]王庆明，李 微.订单型企业多目标生产计划的制定及其调度[J].机电工程，2012，29（6）：621-626.