焊接机器人运动学分析及轨迹规划研究

刘 鹏，宋 涛，贠 超，高志慧

（北京航空航天大学 机械工程及自动化学院，北京 100191）

0 引 言

随着工业自动化技术的提高，焊接机器人技术日趋成熟，现已大量应用到工业生产中。为实现对石化容器、梁构等大型焊件的自动焊接，笔者所在的课题组与北京中电华强焊接工程技术有限公司联合研制了7 自由度大型焊接机器人“中电一号”。

为了保证焊接质量，弧焊机器人作业过程中，不仅对末端执行器（焊丝）的位姿、速度及加速度有很高的要求，而且要求运动轨迹为连续平滑的曲线。因此研究者需要建立机器人运动模型，并对其运动轨迹进行规划，从而满足焊接工作的要求。

本研究运用D-H 坐标系理论，分析该机器人的运动学问题[1]；并在运动学分析的基础上，在关节空间采用三次多项式函数插值法，研究机器人轨迹规划的问题；最后在Matlab7.8 平台上，运用机器人工具箱[2]进行仿真，以验证轨迹规划的合理性。

1 运动学分析

1.1 机器人结构分析及D-H 坐标系建立

“中电一号”是个7 自由度关节式机器人，其结构图如图1 所示。该机器人由腰部、大臂、小臂和腕部等部分组成，所有关节均为转动关节。

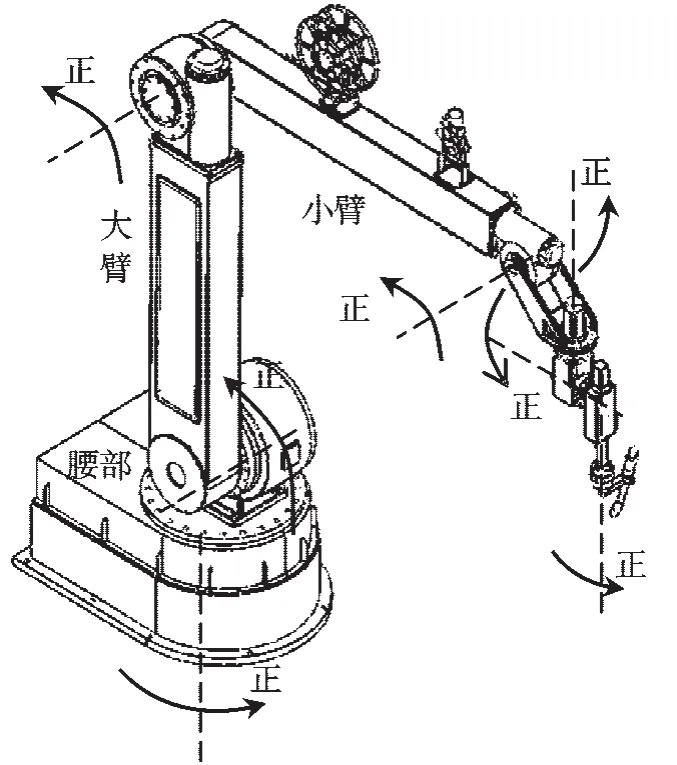
图1 7 自由度机器人结构图

从理论上来说，该7 自由度机器人为冗余度机器人。但是实际上，机器人的第7 关节仅是为了满足焊接工艺需要，使焊枪在焊接过程中保持转动，不对机器人末端的运动轨迹产生影响。因此，研究者在进行运动学分析时，只需建立前6 个关节的运动学模型。

本研究按照D-H 方法建立其连杆坐标系，D-H 坐标系的建立如图2 所示。

图2 D-H 坐标系的建立

1.2 机器人正逆运动学分析

1.2.1 运动学正解

D-H 参数表如表1 所示。

根据连杆坐标系和D-H 参数表，机器人运动学方程可描述为：

式中：i-1iT—第i 个连杆坐标系相对于第i-1 个连杆坐标系的齐次变换矩阵。

且有：

式中：cθi=cosθi，sθi=sinθi，cαi=cosαi，sαi=sinαi(i=0,1…6)。

表1 D-H 参数表

将表1 中的连杆参数代入到式（1，2）中，得到机器人末端相对于基坐标系的位姿矩阵60Τ 。同时，末端在基座标系下的位姿亦可表示为：

式中：

1.2.2 运动学逆解

机器人逆运动学求解一般有两种方法：封闭解法和数值解法[3]。封闭解法计算速度快，效率高，便于实时控制；数值解法是一种迭代法，不能求出所有的解。对于本研究设计的焊接机器人，由图2 可以看出，其第2、3、4 关节轴相互平行，在结构上满足Pieper 准则[4]，可以采用封闭解法。因此，本研究采用封闭解法来求解该逆运动学问题，则：

（1）求解 θ1。

在式（3）两端同乘以01T-1，式（4）左边第2 行第4 列元素为常数，将等式对应元素等同起来，可得：

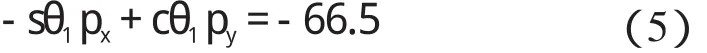
由三角代换可得：

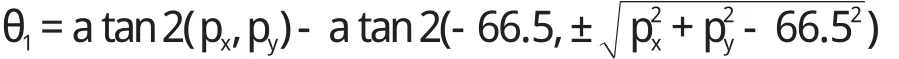
其中，正、负号对应的两个解对应着θ1的两个可能。

（2）求解 θ5。

在确定θ1的一个解之后，再观察方程式（4）两端第2 行前3 个元素，联立等式，可求得：

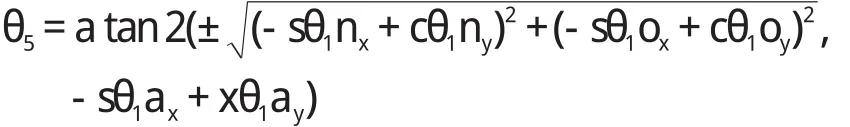
（3）求解 θ6。

令等式（4）两端第2 行第1 列及第2 行第2 列元素对应相等，则有：

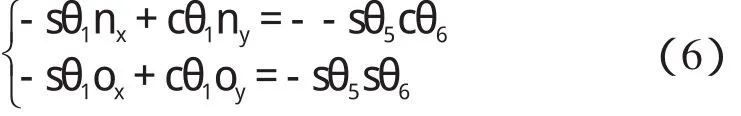
如果 sθ5≠ 0，则可解得：

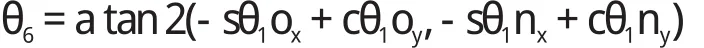
（4）求解 θ2。

令式（4）左右两边第1 行第3 列、第3 行第3 列元素对应相等，则有：

若 sθ5≠ 0，可解得：

结合式（3），可得下列关系式：

若 sθ5≠ 0，则令：

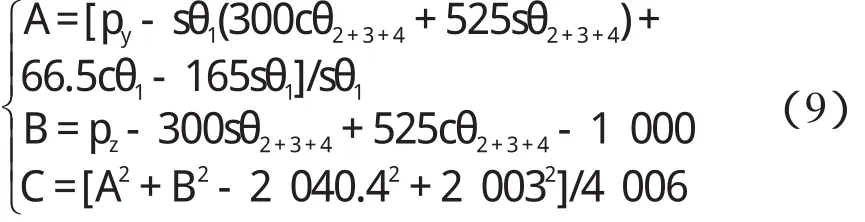
通过上式可解得：

（5）求解 θ3。

结合式（8，9），有：

进而可解得：

（6）求解 θ4。

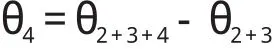
至此，6 个关节变量的逆解均已求得。θ1、θ2 以及θ5有两个解，而θ3、θ4 和θ6 均只有一个解。因此满足Pieper 准则的机器人最多有8 组解，但受关节转动范围的限制，某些解是伪解，不可实现[5]。

1.3 雅克比求解

焊接速度的均匀与否，直接关系着焊接质量的好坏[6]。因此，本研究必须通过雅克比对机器人进行速度的规划。对于n 个关节的机器人，雅可比矩阵是6 ×n 矩阵，前3 行代表对夹手线速度v 的传递比，后3行代表对夹手角速度ω的传递比，即：

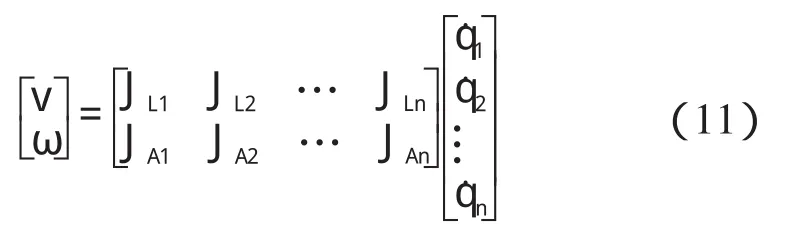
式中：n=6；雅克比矩阵—6 ×6 方阵；JLi，JAi—关节i 的单位关节速度引起夹手线速度和角速度。

本研究采用微分变换法求解雅克比矩阵。

因为中电一号各个关节为转动关节，对于任意的关节i，连杆i 相对于连杆i-1 绕坐标系{}i 的zi 轴所作微分运动dθi，其微分运动矢量为：

由微分变换公式[7]，可解得夹手相应的微分运动矢量为：

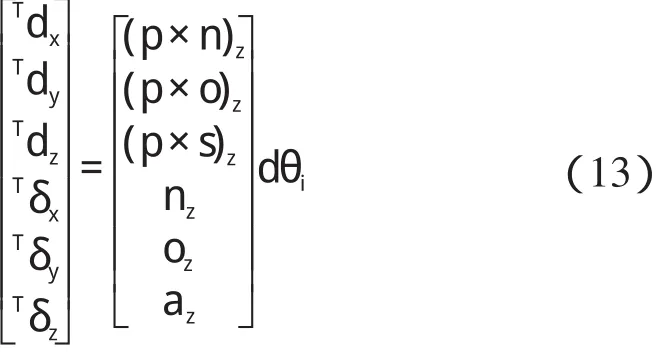
因此，可得雅克比矩阵J(q)的第i 列如下：

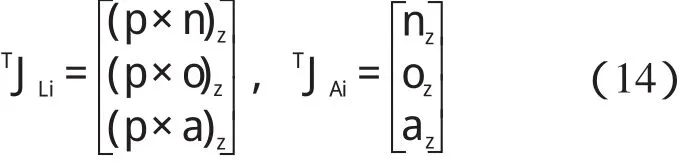
式（12～14）中：i=1,2…6；n,o,a,p—niT 的4 个列矢量。

受篇幅所限，对于雅克比矩阵各元素的具体数值，本研究不再给以表述。下文将在机器人运动学分析的基础上，对其轨迹规划进行研究。

2 轨迹规划

关节空间的轨迹规划具有计算简单、不发生机构奇异性等特点[8]。关节空间的轨迹规划有抛物线过渡线性插值、三次多项式插值、五次多项式插值及B 样条插值法[9]。综合考虑系统的稳定性及控制的实时性，本研究在三次多项式插值法的基础上，在关节空间构造了过路径点的三次多项运动路径。该算法简单、计算量小，且具有较高的控制精度，结合研究课题需要，本研究采用该算法进行关节空间轨迹规划的研究。

2.1 笛卡尔空间到关节空间转化

假设笛卡尔空间有一连续轨迹被离散为n 个空间位姿节点序列{T}，其上任意两个相邻的节点的位姿可表示为Ti、Ti+1，速度可表示为[viωi]T和[vi+1ωi+1]T。

根据1.3.2 部分内容，可求得两节点所对应的两组关节角度为 Θi、Θi+1；由1.4 节部分的内容，可推导出：

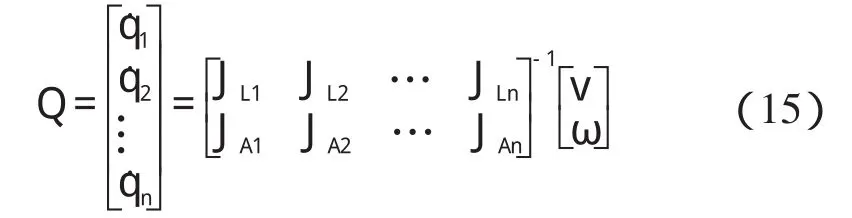
由式（15），从而求得其对应的关节速度为Qi和Qi+1。因此，对笛卡尔空间轨迹的规划可间接转化为对关节空间的轨迹规划。

2.2 过路径点的三次多项式插值

根据2.1 节中假设，在机械手运动过程中，需经过n 个空间位姿点。这n 个位姿点对应着关节空间的n组关节角度，也就意味着关节空间中各关节必过这n组关节角度。

对任意两组相邻的关节角度，本研究取其中某个关节进行分析，称该关节前一个关节角度θi为起始点θ0，则后一个关节角度θi+1为终止点θf。该段运动轨迹的描述，可用起始点关节角度与终止点关节角度的一个平滑插值函数θ(t)来表示，θ(t)在t0=0 时刻的值是θ0，在终端时刻tf的值是终止关节角度θf。

为了实现单个关节的平稳运动，轨迹函数θ(t)至少需要满足4 个约束条件。其中，两个约束条件是起始点和终止点对应的关节角度：

为了满足关节速度的连续性要求，在起始点和终止点的关节速度须满足：

设三次多项式的表达式为：

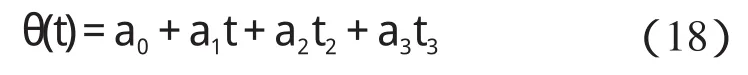
则结合式（16，17）可以求得三次多项式的系数如下式所示：

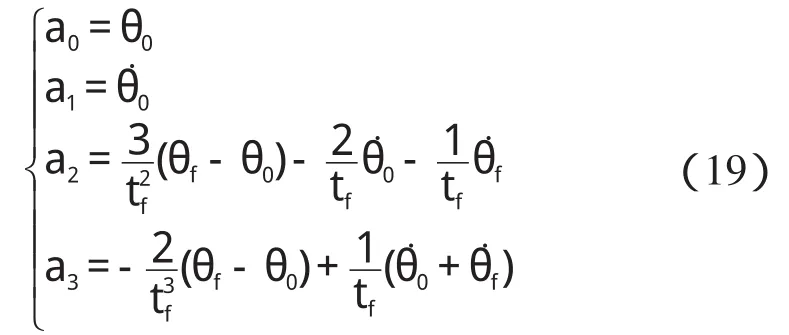
式中：θ0，θf，θ˙0，θ˙f—起始点和终止点的角度和角速度。

关于它们的求解方式，2.1 节中已阐述，不再赘述。

3 仿真验证

本研究以Matlab7.8 为实验平台，运用机器人工具箱，对机器人运动学、轨迹规划进行仿真分析[10]。

3.1 运动学建模

笔者运用机器人工具箱，结合D-H 参数，编写相关代码，以建立机器人模型：

3.2 运动学仿真

本研究假设机器人初始关节角度为q0=[0 0 0 0 0 0]，经历2 s 运动到N（2.386，-0.066，2.431）时的关节角度为qn=[0 1.625-1.644 0.019 1.57 0]。

由运动学方程，可求得机器人末端初始位姿矩阵为：

机器人末端终止位姿矩阵为：

仿真中机器人将平稳地从初始位姿运动到终止位姿。机器人末端运动轨迹如图3 所示。

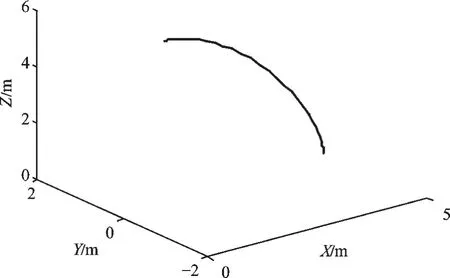
图3 机器人末端运动轨迹

通过仿真，可以观察到机器人各关节运动平稳，验证了连杆参数设计的合理性和正解算法的正确性。

3.3 关节空间轨迹规划仿真

根据机器人末端轨迹，本研究通过运动学反解得出各关节位移，由逆雅克比求出关节速度。再利用三次多项式进行插值，分别计算出6 个关节各自对应的a0，a1，a2，a3，实现各个关节的轨迹规划。

本研究以Robotics Toolbox 为工具，验证关节空间三次多项式插值规划的合理性。假设机器人为刚体，末端没有负载，仿真时间为2 s，机器人各关节从q0=[0 0 0 0 0 0]，运动到 qn=[p i/6 pi/5 pi/4 pi/3 pi/2 pi/1]，各变量随时间变化的曲线图如图4 所示。

从图4 中可以看出，各个关节的速度及加速度曲线连续且平滑，对各关节既无刚性冲击又无柔性冲击，故基本能够满足控制要求。同时也证明了机器人各连杆参数设计的合理性，以及基于关节空间的轨迹规划方法的可行性。该技术目前已应用于机器人点焊、角焊作业中，实际使用效果较好。

4 结束语

本研究运用D-H 坐标系理论，研究了“中电一号”焊接机器人的运动学问题，并在运动学分析的基础上，采用过路径点的三次多项式函数插值法，实现了机器人在关节空间的轨迹规划。

在Matlab7.8 平台上，本研究建立了机器人运动学模型，对机器人运动学问题和关节空间轨迹规划进行仿真验证。仿真结果表明，机器人连杆参数设计合理、运动学模型建立正确，同时也验证了基于关节空间的三次多项式函数插值算法的轨迹规划方法合理可行，为机器人动力学及焊接机器人今后在马鞍面多层多道焊接的研究打下了基础。

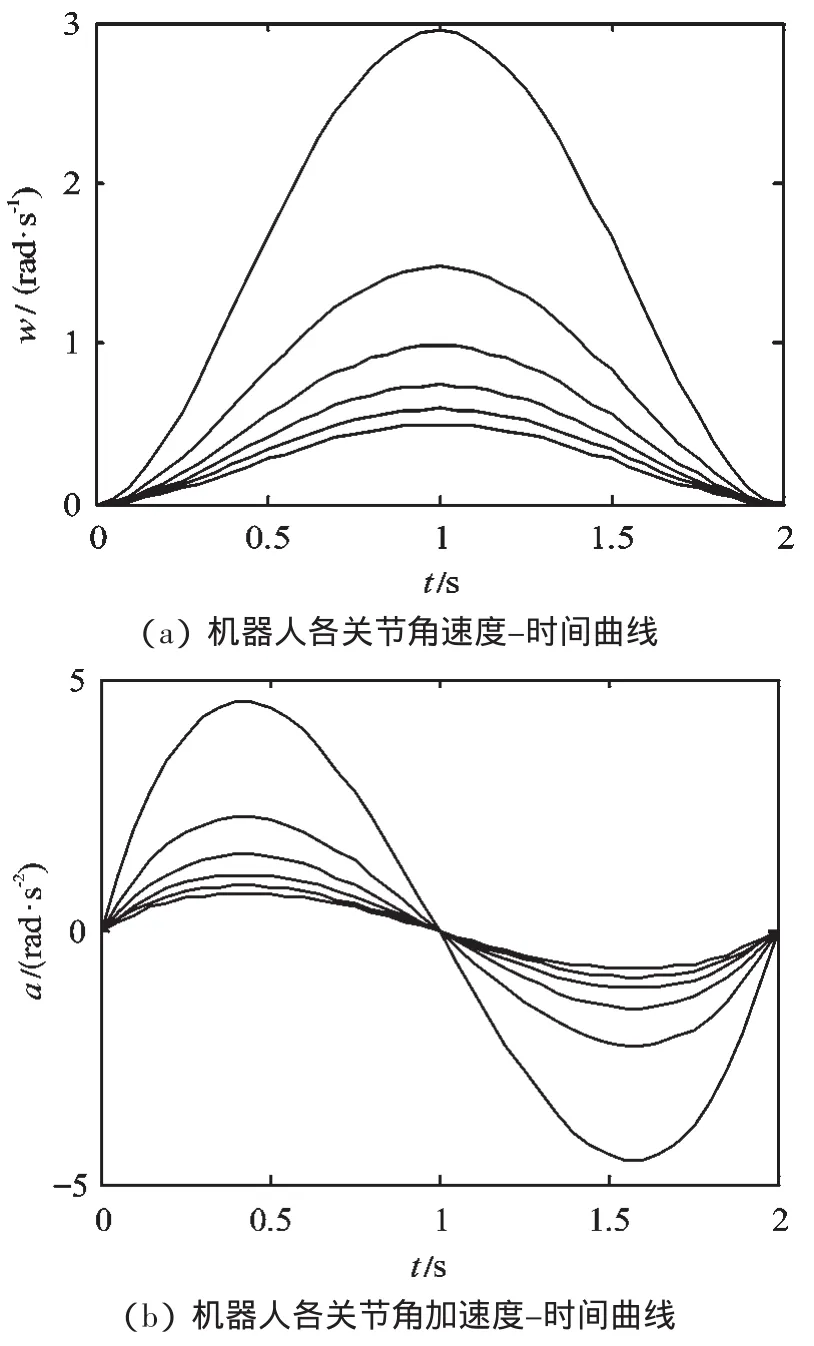
图4 各变量随时间变化的曲线图

（References）：

[1]刘松国.六自由度串联机器人运动优化与轨迹跟踪控制研究[D].杭州：浙江大学流体传动及控制国家重点实验室，2009.

[2]谢 斌，蔡自兴.基于Matlab Robotics Toolbox 的机器人学仿真实验教学[J].计算机教育，2010（19）：140-143.

[3]熊有伦.机器人学[M].北京：机械工业出版社，1993.

[4]吕世增，张大卫，刘海年.基于吴方法的6R 机器人逆运动学旋量方程求解[J].机械工程学报，2010，46（17）：35-41.

[5]王 伟，谢明红，周国义.6-DOF 工业机器人逆解优化及其工作空间的研究[J].机械与电子，2011（1）：57-60.

[6]毛志伟，李舒扬，葛文韬，等.移动焊接机器人大折角角焊缝跟踪及工艺[J].焊接学报，2011，32（2）：33-36.

[7]蔡自兴.机器入学[M].北京：清华大学出版社，2000.

[8]KUBOTA N，ARAKAWA T.Trajectory generation for redun⁃dantmanipulator using virus evolutionary genetic algorithm.[C]//Robotics and Automation，1997-Proceedings，IEEE In⁃ternational Conference on Albuquerque，USA：IEEE，1997：205-210.

[9]冯晓波.机器人准确制孔技术研究[D].杭州：浙江大学机械工程学系，2011.

[10]程永伦，朱世强，罗利佳，等.基于Matlab 的QJ-6R 焊接机器人运动学分析及仿真[J].机电工程，2007，24（11）：107-110.