基于数学形态学的汽车轮毂单元振动信号消噪算法研究*

孟庆华，侯舟波，孙晓红

（杭州电子科技大学 机械工程学院，浙江 杭州 310018）

0 引 言

汽车轮毂单元是将与轮毂轴承相配套的零件即轮毂或转向节和轴承圈套制成一体的结构。汽车轮毂轴承单元的主要作用是承受汽车的重量，并传输动力至轮胎。其受力包括径向载荷与轴向载荷，是非常重要的安全件。因此，实时监测轮毂单元的运转状况，对于提高行车安全、防止安全事故具有重要意义。

在运转过程中，包含局部缺陷的汽车轮毂单元会产生间断性的脉冲冲击激振，使所测振动信号包含快速衰减的脉冲响应分量。这种瞬时频率突变的持续时间极短，同时所测振动信号包含测量噪声、表面波纹度引起的振动等干扰，脉冲冲击特征往往被淹没。因此，在强噪背景下有效提取信号中的脉冲冲击成分是轮毂单元故障诊断的关键。随着小波分析与奇异值分解在信号降噪中的应用[1-3]，信号降噪技术取得了一定的进展。但是小波降噪与奇异值分解分别由于阈值选取和奇异值选择的不确定性，导致降噪效果受到影响。

数学形态学[4]（Mathematicalmorphology）是基于积分几何和随机集论建立起来的非线性图像（信号）处理、分析工具，已在图像处理[5]、模式识别、形状分析等方面得到广泛应用。数学形态学还具有十分有效的非线性滤波功能，其信号处理的效果只取决于待处理信号的局部形状特征，而不需要信号的频域信息，并且其算法只有加、减法和取极值计算，不涉及乘除法，运算速度快。近年来逐渐被引用至一维信号分析领域，在电力系统[6-7]、振动[8-9]、心电[10-12]以及语音信号[13]处理中得到了逐步应用。

为了对汽车轮毂单元振动信号进行有效消噪，本研究提出基于数学形态学运算和软阈值的振动信号消噪方法。该算法只涉及加减和取极值计算，运算简单且执行高效，适用于汽车轮毂单元故障的在线监测与诊断。

1 数学形态学基本原理

数学形态滤波是基于信号的几何特征，通过结构元素探测目标信号的位置，以实现对信号的匹配，从而达到信号提取、细节保持及噪声抑制的目的。数学形态学基本运算包括腐蚀、膨胀运算，以及由此构造出的开、闭运算等。

设原始信号 f(n) 为定义在F=(0,1,…,N-1)上的离散函数，定义结构元素b(n) 为 B=(0,1,… ,M−1)上的离散函数，且N M，则 f(n) 关于b(n) 的腐蚀“Θ ”和膨胀“⊕”分别定义为:

f(n) 关于b(n) 的开运算“°”和闭运算“·”分别定义为：

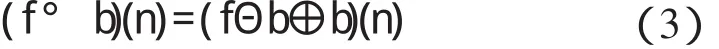
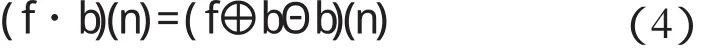
开、闭运算以不同方式平滑信号，在信号滤波中应用普遍。其中，开运算抑制信号的正脉冲（波峰），闭运算抑制信号的负脉冲（波谷）。

2 基于形态学的消噪算法研究

形态学滤波的性能主要取决于结构元素b(n) 的宽度M，当信号中噪声脉冲的宽度不超过结构元素宽度时，噪声脉冲可被开、闭运算去除。本研究为有效抑制噪声正、负脉冲，可采用开—闭（FOC）、闭—开（FCO）运算组合的形态学滤波运算（Morphology Filter，MF），如下式所示：

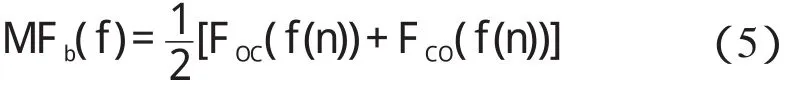
其中：

由于轮毂轴承单元振动信号与噪声的时频特性不同，若结构元素宽度合适，其形态学滤波运算结果中将保留信号大部分的特征波形，而脉冲冲击的峰谷信息和高频噪声则被过滤。由原始信号减去形态学滤波运算结果可得到过滤信号，即形态学峰谷提取结果，通过对其进一步处理就可以得到原始信号中被除去的峰谷信号。定义信号 f 关于b()n 的形态学峰谷提取运算（peak valley extract，PVE）为：

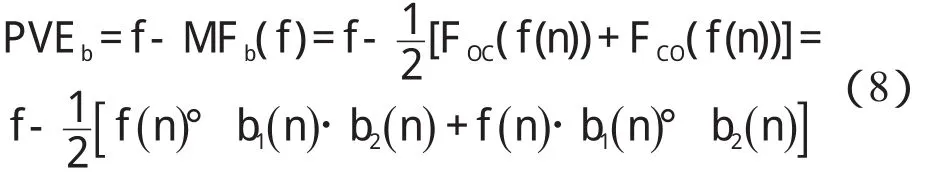
经处理后的形态学运算提取的峰谷信号与形态学滤波的结果相加，可以作为汽车轮毂单元振动信号消噪处理的最终结果。该结果在最大限度去除噪声的前提下，较完整地保留了有用信号。进一步分析该结果可实现轮毂轴承单元的故障检测与诊断。

综上分析，本研究提出基于形态学运算和软阈值的轮毂单元振动信号消噪算法，并在这一基础上对信号进行特征提取，基本流程如图1 所示。

2.1 形态学滤波及峰谷提取

结构元素在数学形态运算中的作用类似于一般信号处理中的过滤窗口，其形状和大小的选取对于信号分析至关重要。结构元素的结构主要有扁平型、直线型、三角形、圆形及其他多边形等，本研究针对信号受随机噪声和脉冲冲击影响的特点，采用菱形和椭圆形结构元素，菱形结构元素对脉冲噪声有较好的滤波效果，椭圆形结构元素用于对随机噪声信号的过滤，宽度取信号最大值的1/50～1/10[14-16]。

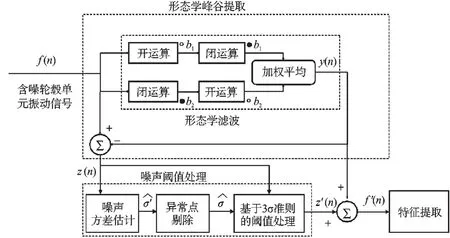
图1 基于数学形态学和软阈值处理的轮毂单元振动信号消噪算法流程图

本研究将菱形结构元素b1(n) 和椭圆形结构元素b2(n) 代入式（6，7），可得到：

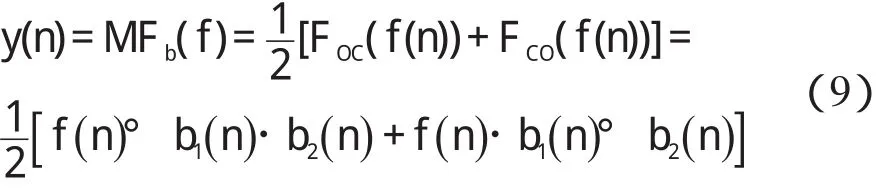
则峰谷提取信号结果为：

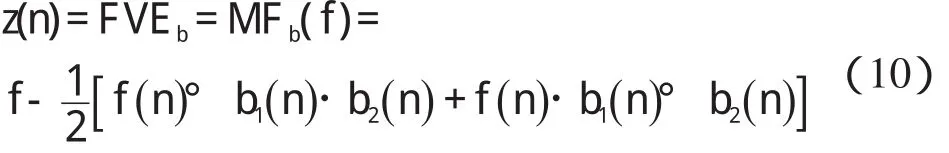
在形态学运算时，结构元素的宽度越大，所滤除的噪声干扰越多，但同时也损失了大量有用信号；反之，结构元素的宽度越小，保留的有用信号越多，但滤除的噪声干扰也越少。通过多次试验，本研究选取b1的最大宽度为5，b2的最大宽度为12 时，取得了较好的试验效果。

2.2 基于3σ准则的软阈值处理

本研究采用适当宽度的结构元素对汽车轮毂轴承单元振动信号进行形态学滤波运算后，脉冲冲击在形态学峰谷提取结果中表现为少量尖峰，而噪声的峰谷信息则为主导因素，且呈现高斯白噪声的分布规律。由统计学3σ准则[17]可知，如果峰谷信号中噪声信号的均值为 μ，方差为σ2，那么其取值几乎全部（约占99.7%）集中在[μ-3σ,μ+3σ]内。另外，由于峰谷信号中脉冲冲击成分的瞬时幅值通常明显高于噪声幅值，可看作噪声信号中的突变点。本研究将3σ准则应用于峰谷信号阈值处理中，可在保留有用信号的同时，将故障特征（脉冲冲击）和噪声区分开。

该算法的具体步骤如下：

（1）计算峰谷提取信号的均值和方差。首先，剔除有用信号干扰，对峰谷提取信号分别求均值μ′和方差 σ′2，将信号中数值在 [μ′-3σ′,μ′+3σ′]外的点剔除，并用 μ′-3σ′或 μ′+3σ′代替，得到新的峰谷提取信号；然后对新的峰谷提取信号再次求均值μ和方差σ2。

（2）对峰谷信号z(n) 进行阈值处理。本研究将峰谷提取信号中幅值在[μ-3σ,μ+3σ]内的点认为是噪声而舍弃，其他点认为是轮毂单元故障信号予以保留。具体计算如下式所示：

式中：z′()

n—经阈值处理后的峰谷信号。

2.3 形态学滤波结果与阈值化峰谷信号求和

本研究把形态学滤波结果y(n) 和经阈值处理后的 峰 谷 信 号 z′(n) 相加，得到 最 终 消噪处理结果f′(n)，如下式所示：

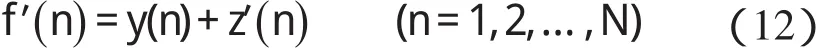
3 仿真与试验信号分析

为检验所提出算法的有效性，笔者分别对仿真信号和轮毂单元振动试验信号进行消噪。本研究采用Matlab 对所提出的算法进行了仿真实验验证。

3.1 仿真实验

设采样频率 fs为10 kHz，采样长度L 为2 000 点，则采样时间为：

正常振动信号为：

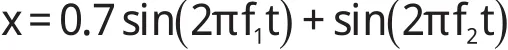
式中：f1，f2—50 Hz、120 Hz；故障信号 p()t—幅值为3mV 的脉冲信号；n()t—白噪声信号。

则染噪故障信号为：

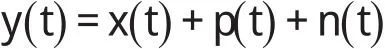
以上仿真信号时域波形如图2 所示。

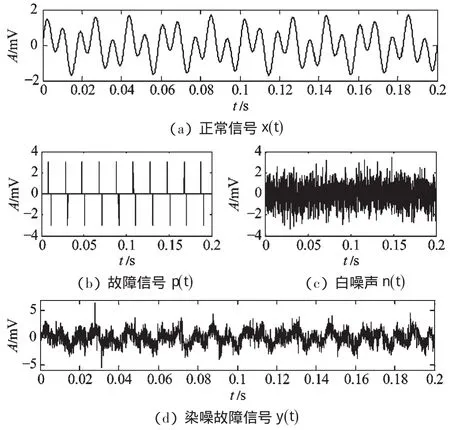
图2 仿真试验信号建模

用传统形态学滤波方法、小波降噪方法（db3 小波基、软阈值）及本研究方法的信号消噪结果以及频域分析结果如图3、图4 所示。其中，用传统形态滤波器滤波后的信号的时域波形如图3（a）所示；用bd3 小波基分解重构的信号时域波形如图3（b）所示；用本研究方法处理得到的信号的时频波形如图3（c）所示，箭头标注位置为识别的故障信号位置，大多数可被明显观察到。含噪故障信号频域图如图4（a）所示；用db3 小波基分解重构的信号频谱图如图4（b）所示；用本研究方法消噪处理后所得到信号的频域分析图如4（c）所示。无噪故障信号的时域波形及频谱分析结果如图5所示。

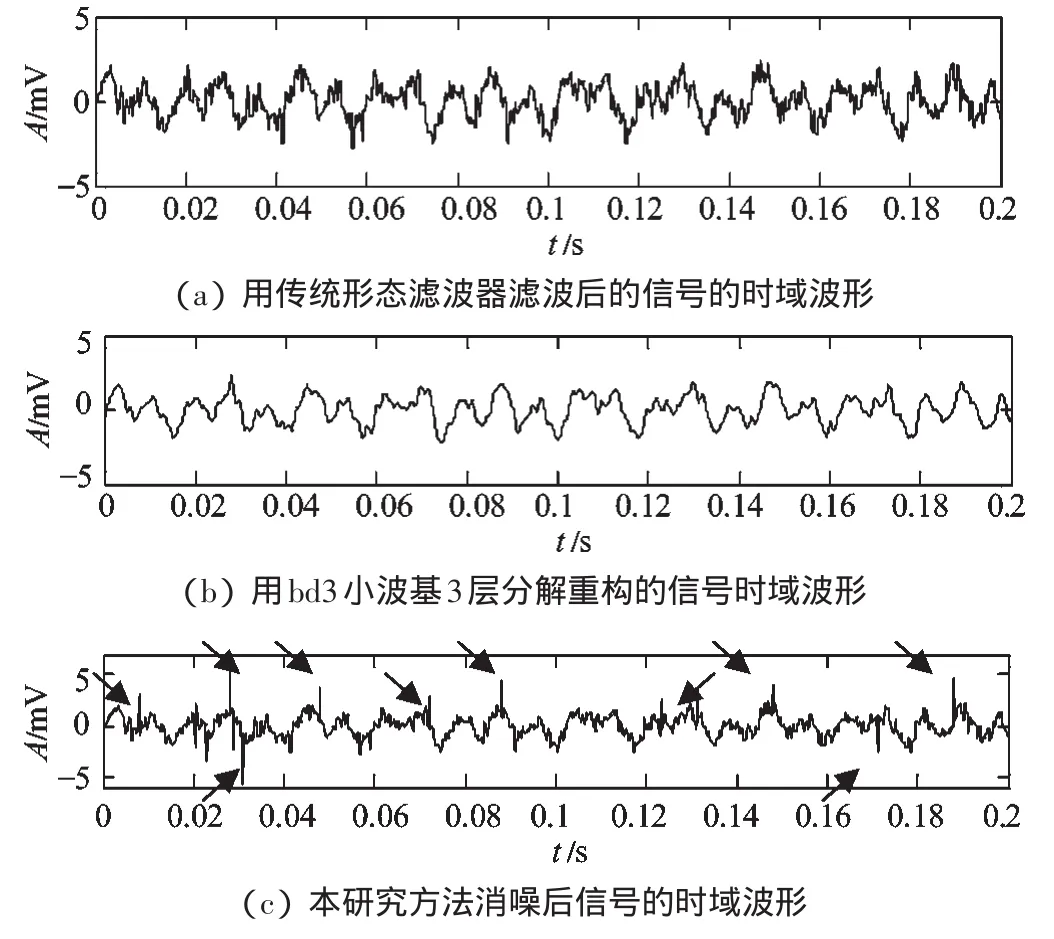
图3 受随机噪声干扰的故障信号消噪仿真试验

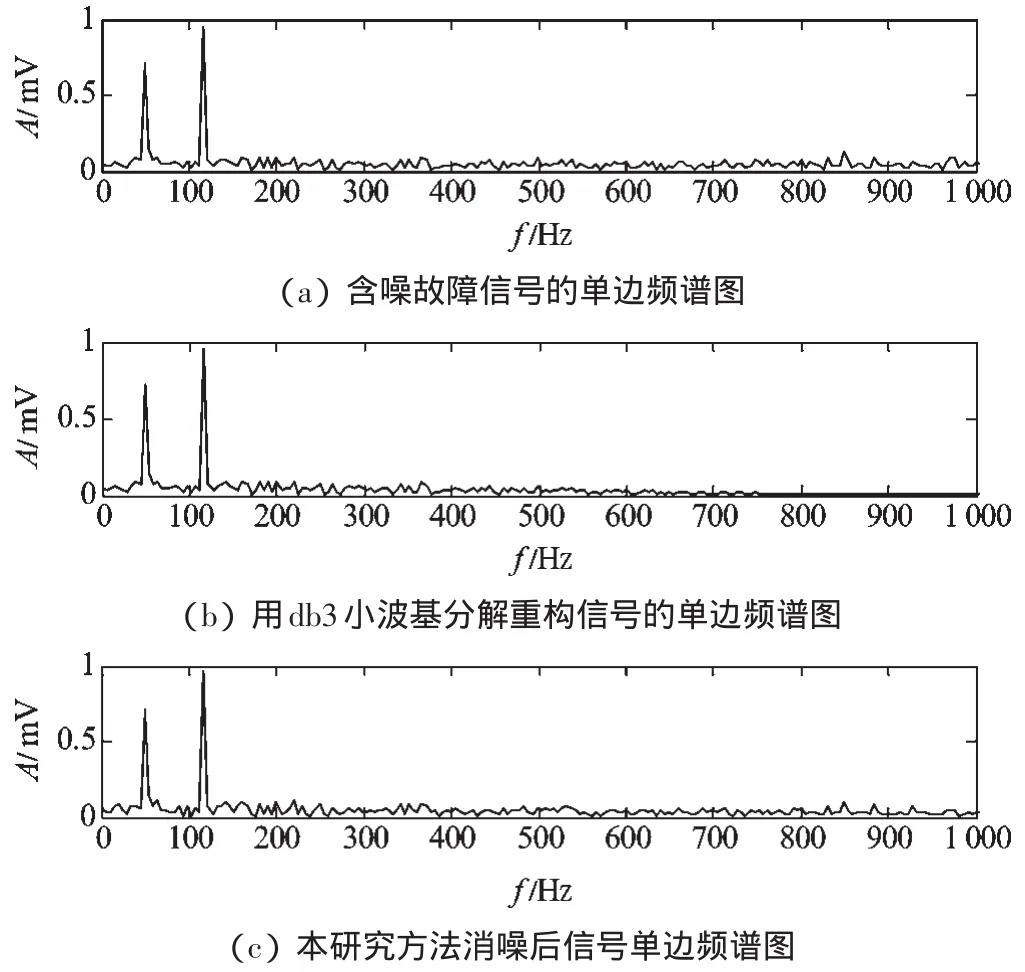
图4 受随机噪声干扰的故障信号及消噪后信号的频谱分析结果

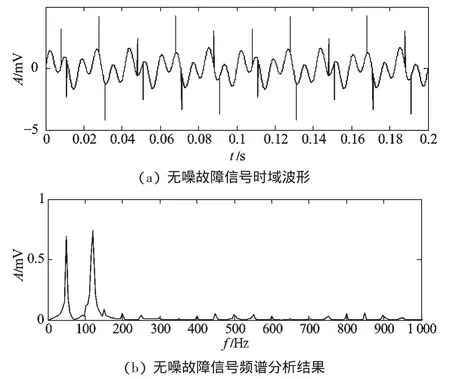
图5 无噪故障信号的时域仿真和频谱分析结果

从仿真结果中可以看出：传统形态学滤波器在过滤大部分噪声的同时，也滤掉了脉冲信号，即故障信号无法识别；小波消噪方法在阈值选择上存在一定难度，本研究采用软阈值消噪，得到的结果中仅保留了部分故障信号，但是由于能量泄漏较大，故障点位置的幅值较小，不易识别；本研究提出的方法在时域可以明显观察到故障信号，但是由于结构元素的宽度没达到最优，在滤波过程中有部分噪声信号未能消除，反映在频域上的频谱分析结果不如小波消噪的好；观察图3（c）中频率800 Hz～1 000 Hz 的范围，具有与图4（b）相同的脉冲信号的频谱特征，由于脉冲信号能量较小，特征不够明显。从总体分析，该算法只有加减法和取极值计算，不涉及乘除法，运算速度快，且对故障的识别效果很明显，因此具有较大的优势。

3.2 试验信号分析

试验对象为浙江某企业制造的轮毂单元，本研究对其在不同工况下的运行状况，分别采集了磨合期、磨合后及运转95 h 后在不同工况下的数据信号。具体工况为300 r/min、500 r/min、700 r/min 等不同转速和0.2 g、0.4 g、0.6 g 等不同负载下的9 种组合。采样频率为10 240 Hz，采样时间各10 s。轮毂单元试验台如图6 所示。

图6 轮毂单元试验台

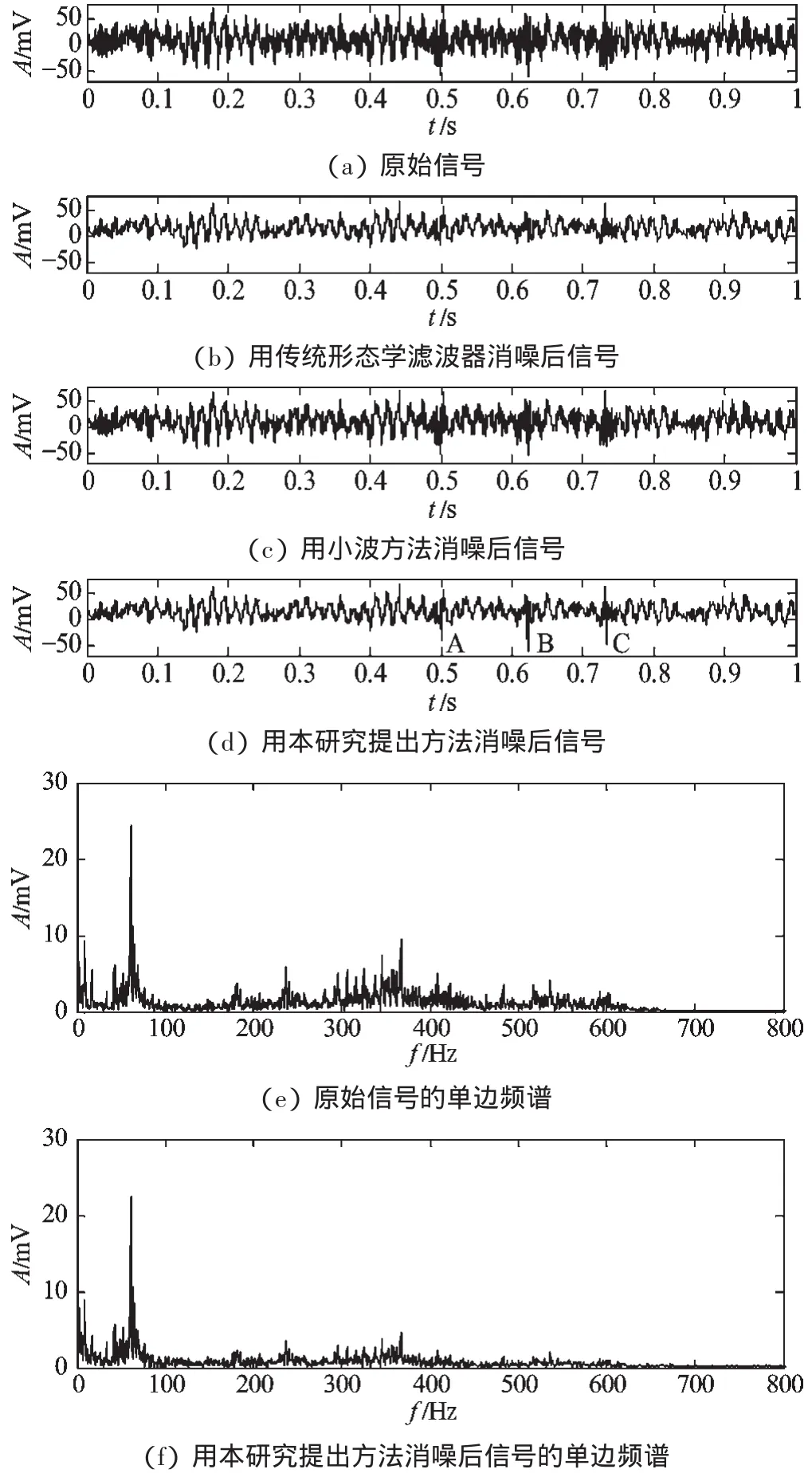
图7 转速500 r/min、负载0.4 g 时信号的时域波形和频谱分析结果

通过对其中运转95 h 后的两种工况：500 r/min、0.4 g 负载及500 r/min、0.6 g 负载下的采集信号，分别采用传统形态学滤波器消噪、小波消噪及本研究提出方法进行信号处理，得到结果如图7、图8 所示。

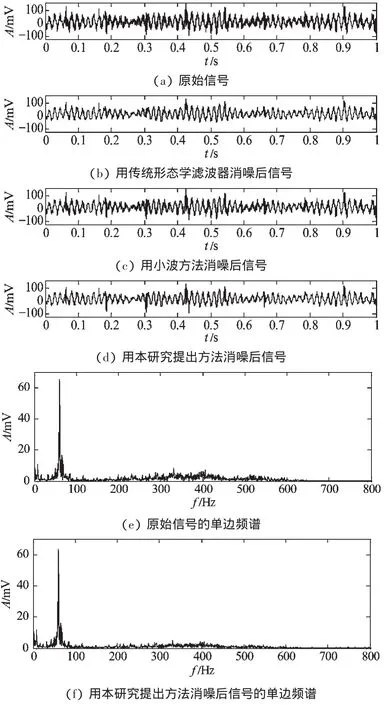
图8 转速500 r/min、负载0.6 g 时信号的时域波形和频谱分析结果

其中，转速500 r/min、负载0.4 g 时信号的时域波形及频谱分析结果如图7 所示。其中，原始信号如图7（a）所示，用传统形态学滤波器消噪后信号如图7（b）所示，用小波方法消噪后信号如图7（c）所示，用本研究提出方法消噪后信号如图7（d）所示；原始信号的单边频谱如图7（e）所示，用本研究提出方法消噪后信号的单边频谱如图7（f）所示；转速500 r/min、负载0.6 g时信号的时域波形及频谱分析结果如图8 所示，其中原始信号如图8（a）所示，用传统形态学滤波器消噪后信号如图8（b）所示，用小波方法消噪后信号如图8（c）所示，用本研究提出方法消噪后信号如图8（d）所示；原始信号的单边频谱如图8（e）所示，用本研究提出方法消噪后信号的单边频谱如图8（f）所示。从频谱图中，得到如下信息：在转速500 r/min、负载0.4 g 这一工况下，在频率范围50 Hz～80 Hz 之间有一段能量集中的频率段，尤其在频率为60 Hz 附近有一个明显的能量集中点，此外，在频率范围350 Hz～400 Hz 之间也有一段能量集中的频率段；在转速500 r/min、负载0.6 g的工况下，本研究同样观察到在频率范围50 Hz～80 Hz之间有一段能量集中的频率段，并且频率为60 Hz 附近有一个明显的能量集中点，而其他频率上没有能量集中的能量带。在时域上，本研究提出的消噪算法在信号消噪结果中可以观察到一定时间间隔的脉冲信号，如图7（d）中A、B、C3 点位置，脉冲信号较其他滤波方法明显。

通过对时域波形和频域波形观察分析可知，本研究提出的消噪算法在保留大部分有用信号的同时，有效地抑制了噪声，且故障信号识别率提高了20%左右。该方法优于形态学滤波和小波消噪方法。

4 结束语

针对汽车轮毂单元振动信号的有用信号往往被背景噪声淹没及故障信号不易识别的特点，本研究提出基于形态学运算和自适应阈值的汽车轮毂单元振动信号消噪算法。通过仿真和试验信号分析，验证了该方法的有效性。该方法与形态学滤波相比，消噪效果更好，相比小波消噪方法，本研究方法运算更简单、高效。

基于形态学运算和自适应阈值的消噪算法有其突出的优点，但还存在如下不足：①该方法在应用过程中，结构元素的选择是个难点，尤其是结构元素的结构和宽度选择，本研究方法所采用的菱形和椭圆形结构元素的宽度值选取参考经验值，一般取信号最大幅值的1/50～1/10，关于结构元素宽度的确定方法还需进一步研究；②基于3σ准则的自适应阈值提取过程中可能将实验数据中的坏点作为故障信号，因此，研究者应将待分析的信号预处理或作进一步分析，需要提出适当的算法对其处理。

（References）：

[1]金 燕，钟金金.基于小波包改进阈值方法的电能质量信号消噪[J].机电工程，2011，28（8）：1012-1014，1018.

[2]陈 果.一种转子故障信号的小波降噪新方法[J].振动工程学报，2007，20（3）：285-290.

[3]吕志民，张武军.基于奇异谱的降噪方法及其在故障诊断技术中的应用[J].机械工程学报，1999，35（3）：85-88.

[4]SERRA J.Image Analysis and Mathematical Morphology[M].New york：Academic，1982.

[5]郭景峰，申光宪，郑绳楦，等.数学形态学在数字滤波中的应用研究[J].机械工程学报，2002，38（10）：144-147.

[6]林湘宁，刘海峰，鲁文军.基于广义多分辨率形态学梯度的自适应单相重合闸方法[J].中国电机工程学报，2006，26（7）：101-106.

[7]郝晓宏，郝守庆，胡振邦.基于模糊自适应形态滤波器和S变换的暂态电能质量扰动检测[J].电力系统保护与控制，2011，39（17）：98-102.

[8]郝如江，卢文秀，褚福磊.滚动轴承故障信号的数学形态学提取方法[J].中国电机工程学报，2008，28（26）：65-70.

[9]章立军，杨德斌，徐金梧，等.基于数学形态滤波的齿轮故障特征提取方法[J].机械工程学报，2007，43（2）：71-75.

[10]SUN Y，CHAN K L，KRISHNAN S M.ECG signal condi⁃tioning by morphological filtering[J].Com puters in Biolo⁃gy and Medicine，2002，32（6）：465-479.

[11]毛 玲，孙即祥，张国敏.基于形态学运算和自适应阈值的心电信号消噪[J].信号处理，2009，25（1）：6-10.

[12]BAI Fang-fang，MIAO Chang-yun，ZHANG Cheng，etal.Studying on De-noising Algorithm of Heart Sound Signal based on the Generalized Mathematical Morphology[C]//IC⁃SP2010 Proceedings：College of information and Communi⁃cation Engineering.Tianjin：[s.n.]，2011.

[13]赵晓群，刘颖娜，武 睿.基于形态滤波的基音检测新方法[J].通信学报，2004，25（5）：53-58.

[14]沈 路.数学形态学在机械故障诊断中的应用研究[D].杭州：浙江大学机械工程学系，2010.

[15]夏其表，王 洁.基于虚拟仪器的精密球研磨加工的振动信号检测[J].轻工机械，2011，29（2）：79-82.

[16]刘文锋，刘文玲.旋转机械振动测量方法确定及分析[J].机电技术，2012（3）：121-130.

[17]金炳陶.概率与数理统计[M].北京：电子工业出版社，1999.