基于三点法的高铁钢轨打磨砂轮磨损检测仿真
2013-09-13刘学士
肖 旭,戴 勇,刘学士
(浙江工业大学 特种装备制造与先进加工技术教育部/浙江省重点实验室,浙江 杭州 310014)
0 引 言
钢轨是机车轨道结构中最昂贵的构件之一,也是机车车辆和轨道之间的接口,钢轨维护的好坏直接影响列车运行安全、旅客舒适度和铁路运营成本。铁路发达国家普遍采用钢轨打磨的方式来消除钢轨表面的病害[1-3]。在钢轨打磨过程中砂轮磨损是不可避免的,砂轮磨损将导致打磨后的轨道截面与设计截面不同,使轮轨的受力发生改变。当砂轮磨损严重时,甚至会出现钢轨病害未能完全去除、钢轨表面质量不达标等情况,这些都将影响钢轨的平顺性。高速铁路列车运行的速度比普通铁路高,对钢轨的平顺性要求也更高。轨道不平顺将严重影响高铁运行的舒适性、安全性和钢轨使用寿命。预计到2020年,中国铁路营业里程将达到12万公里以上,其中铁路快速客运网将达到5万公里以上[4]。面对如此大规模的铁路网,通过在钢轨打磨时实现砂轮磨损的在线检测和自动补偿,不仅能够提高钢轨打磨效率,还能提高打磨质量,对于铁路钢轨的维护具有重要的意义。
目前,对于钢轨打磨的研究主要针对打磨深度、打磨周期、打磨方案和最优截面等,而对钢轨打磨砂轮磨损的检测,尚未见到有关文献报道。砂轮磨损检测方法大都是针对磨床砂轮的,主要有声发射法、计算机视觉法、光电检测法等方法[5-6]。而钢轨打磨环境恶劣,这些方法在用于检测钢轨打磨砂轮磨损时具有一定的局限性,如同时工作的砂轮太多,这些砂轮的声发射相互干扰,使声发射法无法使用;野外光线变化复杂给光学检测带来困难等。
基于以上分析,本研究提出采用三点法对钢轨打磨砂轮磨损进行测量,通过对钢轨打磨前后表面的距离变化间接测量出砂轮的磨损量。
1 三点法测量钢轨表面原理
三点法由Tanaka和Sato于1986年提出,国内外众多学者对其进行了深入研究并提出了多种改进的三点法[7]。经过几十年的发展,三点法广泛用于直线度、平面度、圆度等精密测量中[8-9]。
本研究采用的三点法测量示意图如图1所示。该方法已在挤出平模头的直线度检测中成功应用,提高了挤出平模头的加工精度[10-11]。图1中,左、右两轮用于测量小车的移动称为行走轮;两行走轮之间的距离为2L,称为测量小车的跨距;行走轮1和光电编码器相连,用于测量小车移动的距离。本研究在两行走轮中间安装一个位移传感器,行走轮1、位移传感器、行走轮2与被测表面分别接触于A、B、C三点。规定B点在AC连线上方时,传感器测头上缩,测量值为负;B点在AC连线下方时,测头下伸,测量值为正;测头在AC连线上时,测头不动,测量值为零。由A,B两点纵坐标a,b和传感器的测量值H可以求C点的纵坐标c,其求解公式为:
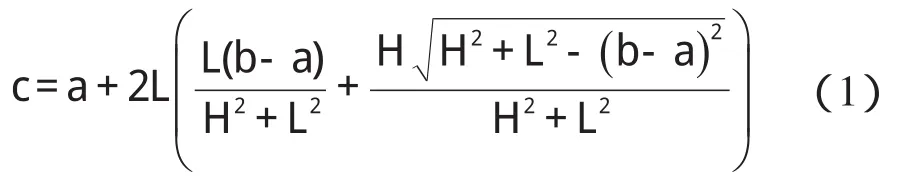
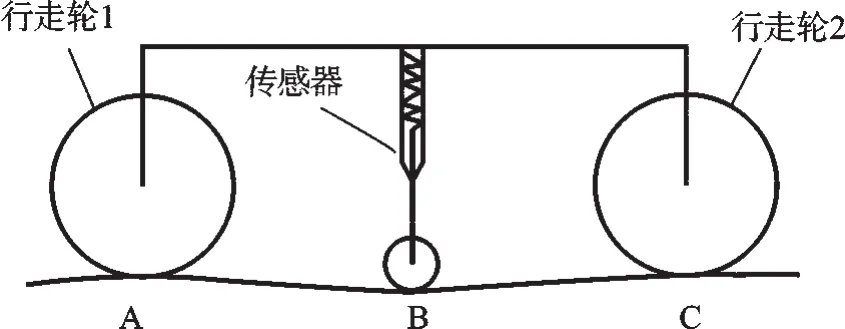
图1 三点法测量示意图
测量小车对钢轨表面进行测量时,由A、B的纵坐标和传感器的测量值,根据公式(1)得到C点纵坐标;然后小车向右平移L,这时行走轮1到达B点,传感器到达C点,根据B、C的纵坐标和传感器的测量值,由公式(1)可以得到下一个被测点的纵坐标。以此类推,测量小车每右移半跨距L就可以得到一个测量点的纵坐标,这样就得到了被测钢轨表面的测量曲线。
曲线参数如表1所示。

表1 曲线参数(单位:mm)
2 测量的影响因素分析
影响三点法对钢轨表面测量的因素有很多,如传感器测量精度、传感器安装精度、行走轮的回转精度、行走轮的安装精度、测量小车的尺寸等。本研究对这些因素进行仿真并对结果进行分析,为元器件的选择、测量小车的制作、测量方案的制定提供依据。
假定打磨前后钢轨面都可以用正弦曲线y=N·s i n(2πx/M)+b表示。根据TB 10754-2010《高速铁路轨道工程施工质量验收标准》可知高铁钢轨的静态高低不平顺标准为2 mm(10 m弦),所以正弦曲线参数如表1所示。由于测量打磨前后表面的距离主要取决于每次测量钢轨表面时的准确程度,本研究以打磨后的表面为例来分析影响测量的因素。
2.1 传感器测量误差的影响
假定传感器的测量误差是在[-1 μm,1 μm]内,且服从正态分布的随机误差,均值μ=0,标准差σ=0.000 3。在仿真过程中本研究先根据被测曲线计算出传感器测量的真值,然后在真值上加上正态分布的随机误差构成传感器的测量值H,再按公式(1)进行仿真。测量小车跨距为2L=2 000 mm,测量50个点时,单次测量结果如图2(a)所示。
为了减小传感器测量时的随机误差对测量结果的影响,本研究采用均值处理的方法即每个点都是间隔为1 mm的3个点的测量值的平均值,其结果如图2(b)所示。
图2(b)的测量结果明显好于图2(a)。两种测量方案的绝对误差如图2(c)所示。
从中可以看出,通过采用均值处理可以大大减小测量时的绝对误差。由于每个点都是取周围点的平均值,这种方法还可以消除测量过程中小车移动的定位误差对测量结果的影响。从图2(c)中还可以看出,传感器的绝对误差随测量次数的增加而逐渐增加,所以测量时研究者应尽量减少测量次数;当L=1 000 mm时,如果测量距离为20 m(点20),测量的绝对误差小于0.02 mm,完全可以满足对钢轨表面的测量。
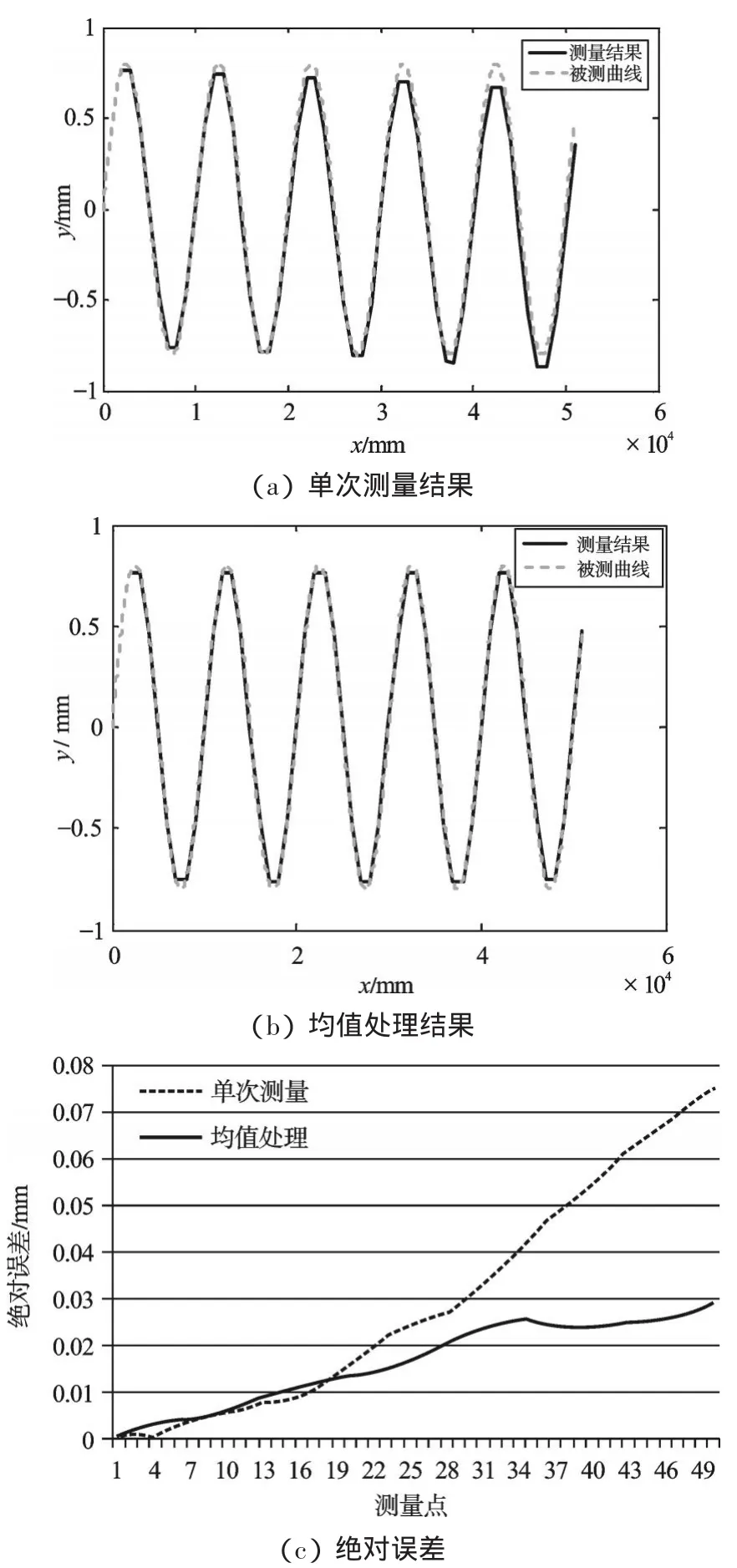
图2 单次测量和均值测量的比较
2.2 传感器安装误差的影响
在测量小车的制作过程中,传感器的安装位置必然存在误差。传感器安装误差将使传感器测量的点与理论的点不同,导致测量值与真值存在偏差,影响测量结果的精度。以传感器安装位置偏离测量小车中心向右侧1 mm为例,其仿真结果如图3(a)所示。测量结果和被测曲线的绝对误差如图3(b)所示。从图3中可以看出,传感器的安装误差对测量结果的影响不大,但测量误差随测量次数的增加有增大的趋势。当测量范围为20 m时绝对误差小于0.015 mm,测量范围为50 m时绝对误差小于0.05 mm。在普通的机械加工中传感器安装的精度远高于1 mm,其测量时的绝对误差也将更小,这完全能满足对钢轨表面的测量要求,因此可以采用一般的机械加工方法对测量小车进行加工。
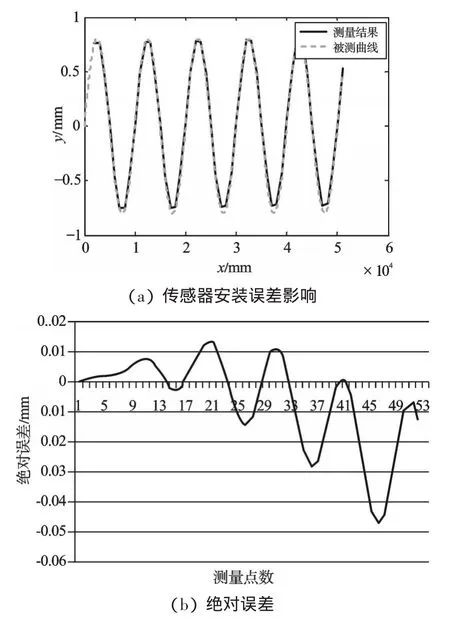
图3 传感器安装误差的影响
2.3 测量小车行走轮回转精度对测量结果的影响
测量小车的行走轮用2个轴承做成。轴承回转误差将使传感器的测量产生误差。假设轴承的实际尺寸大于理论尺寸Δr,则传感器的测头要多伸出Δr/2;若实际尺寸小于理论尺寸Δr,则传感器测头要收缩Δr/2。传感器的输出值变化量:

式中:Δr1,Δr2—两个行走轮相对于理论尺寸的变化量。
根据上文中对传感器测量值符号的规定,Δr大于理论值时为正,小于理论值时为负。
本研究采用向心轴承做行走轮时,这种回转误差就是成套轴承的外圈圆跳动。假设采用的是直径为100 mm的4级轴承,其成套轴承外圈圆跳动误差为6 μm。仿真测量结果如图4(a)所示,从图中可以看出行走轮回转误差对测量结果的影响比较明显。绝对误差如图4(b)所示,当测量范围小于20 m时绝对误差小于0.05 mm,能够满足测量要求,当测量距离为50 m时绝对误差接近0.4 mm,无法满足测量要求,而且误差随着测量距离的增大而逐渐增大。因此,本研究在测量过程中必须控制测量的范围,并选用精度更高的轴承以减小成套轴承外圈圆跳动误差。
根据上述分析可知,对测量结果影响最大的是行走轮的回转误差,而且这些误差对测量的影响都随着测量的次数的增加有增大的趋势。当测量范围为20 m时,这些误差对测量的影响都比较小。因此本研究在制作测量小车时采用常用的加工方法,传感器选用精度为1 μm的位移传感器,行走轮选用2级精度的向心轴承,测量范围选择20 m。
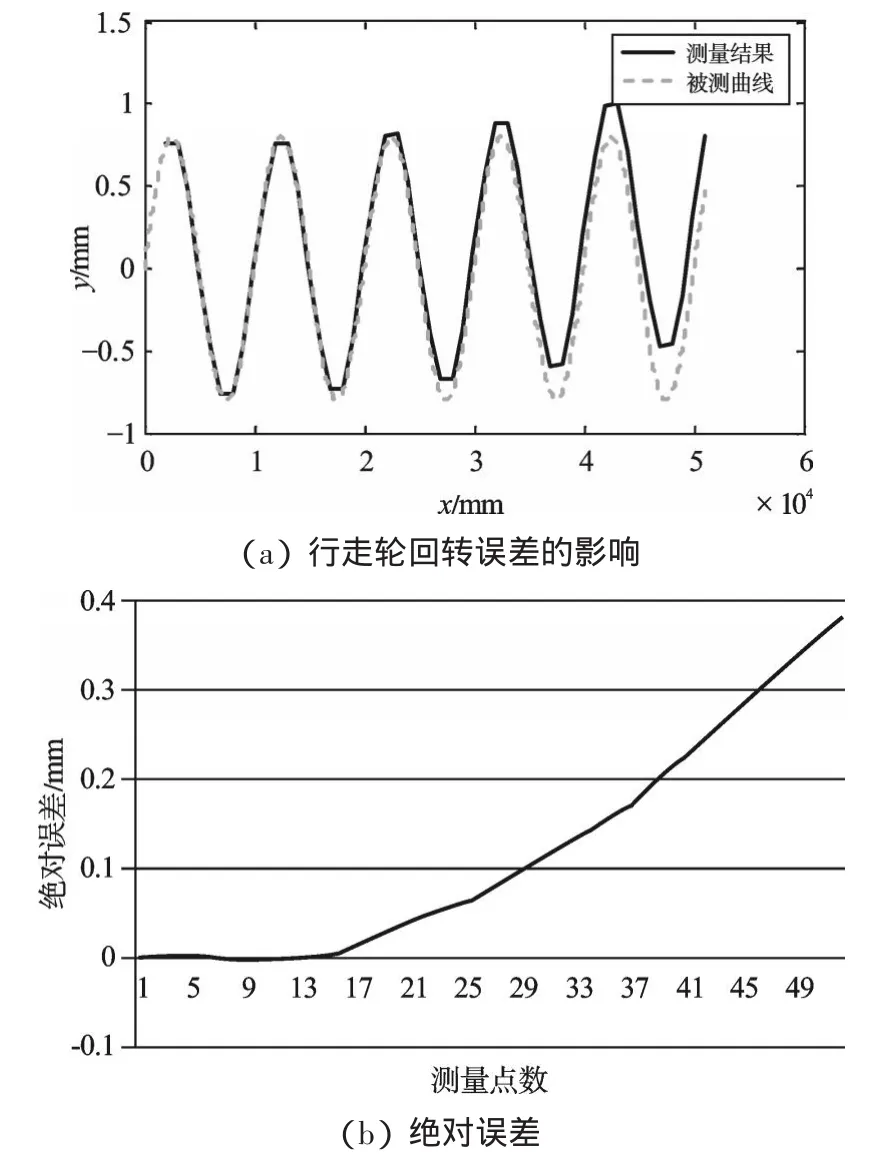
图4 行走轮安装误差的影响
3 测量方案的选择
当采用跨距比较小的测量小车时,在相同范围内的测量点数多,能更好地反映钢轨表面情况,但是累积误差会增大;当测量小车的跨距比较大时,在相同范围内测量的点数变少,不能很细致地反映钢轨表面,但可以减少累积误差,同时可以通过多起点同时测量增加测量点数。
本研究以两种方案(如表2所示)为例测量20 m距离,从表2中可以看出两种方案测量点的密度一致,其仿真结果如图5所示,从图5中可以明显看出,采用方案二测量时的累积误差更小,其结果更接近于被测曲线。
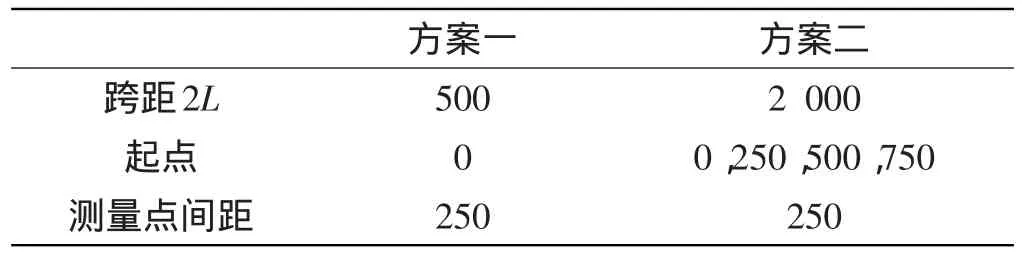
表2 测量方案(单位:mm)
综上所述,本研究采用大跨距、多起点的测量方案(方案二),以减小测量时的累积误差。
4 钢轨打磨砂轮磨损测量仿真

图5 两种测量方案比较
钢轨打磨时砂轮的磨损是不可避免的,砂轮的磨损相当于进给深度的减小,在钢轨上则表现为打磨前表面和打磨后表面之间的距离逐渐减小。假设不考虑打磨过程中的误差复映,通过测量打磨前后表面之间的距离变化就可以间接得到砂轮的磨损量ΔY,即砂轮的磨损量计算公式为:

式中:Δy1,Δy2—两处打磨前表面和打磨后表面的的纵坐标之差。
打磨前表面和打磨后表面距离Δy1和Δy2的测量过程如下,以Δy1为例,测量开始时本研究先让两小车测量同一打磨好的钢轨表面,然后以这个表面作为基准面,两辆测量小车分别测量打磨前和打磨后的一段钢轨表面,通过公式(1)分别计算出打磨前表面的纵坐标和打磨后表面的纵坐标,它们的差的均值就是Δy1,同理可以得到Δy2。由式(3)可以得到砂轮的磨损量。砂轮的磨损是一个缓慢的过程,一小段距离内磨损量几乎为零,Δy1和Δy2都取一段距离内的平均值,这样就可以消除钢轨表面的波动对测量结果的影响。
测量钢轨打磨砂轮的磨损,实际就是测量两个地方打磨前、后表面距离然后计算出距离的差值,因此只需要仿真测量某一处的打磨前、后表面距离就可以验证钢轨打磨砂轮磨损量的测量。被测曲线参数按表1取值,仿真20 m。
仿真结果如图6(a)所示,从图中可以看出两条测量曲线都能很好地反映被测曲线。被测曲线距离变化和仿真测量曲线距离变化如图6(b)所示,从图中可以看出测量曲线距离在被测曲线距离周围波动且随着测量距离的增大有增加趋势,因此再次证明测量范围不能过长。被测曲线的距离变化均值为0.5 mm,测量曲线的距离变化均值为0.508 mm,两者绝对误差为0.008 mm,相对误差为1.6%,能够满足钢轨打磨砂轮磨损的测量要求。
综上所述,本研究选用测量精度为1 μm的位移传感器,直径为100 mm的2级向心轴承为行走轮,测量小车跨距为2 000 mm;测量方案选用方案二,测量时每个点都取周围几个点的均值。
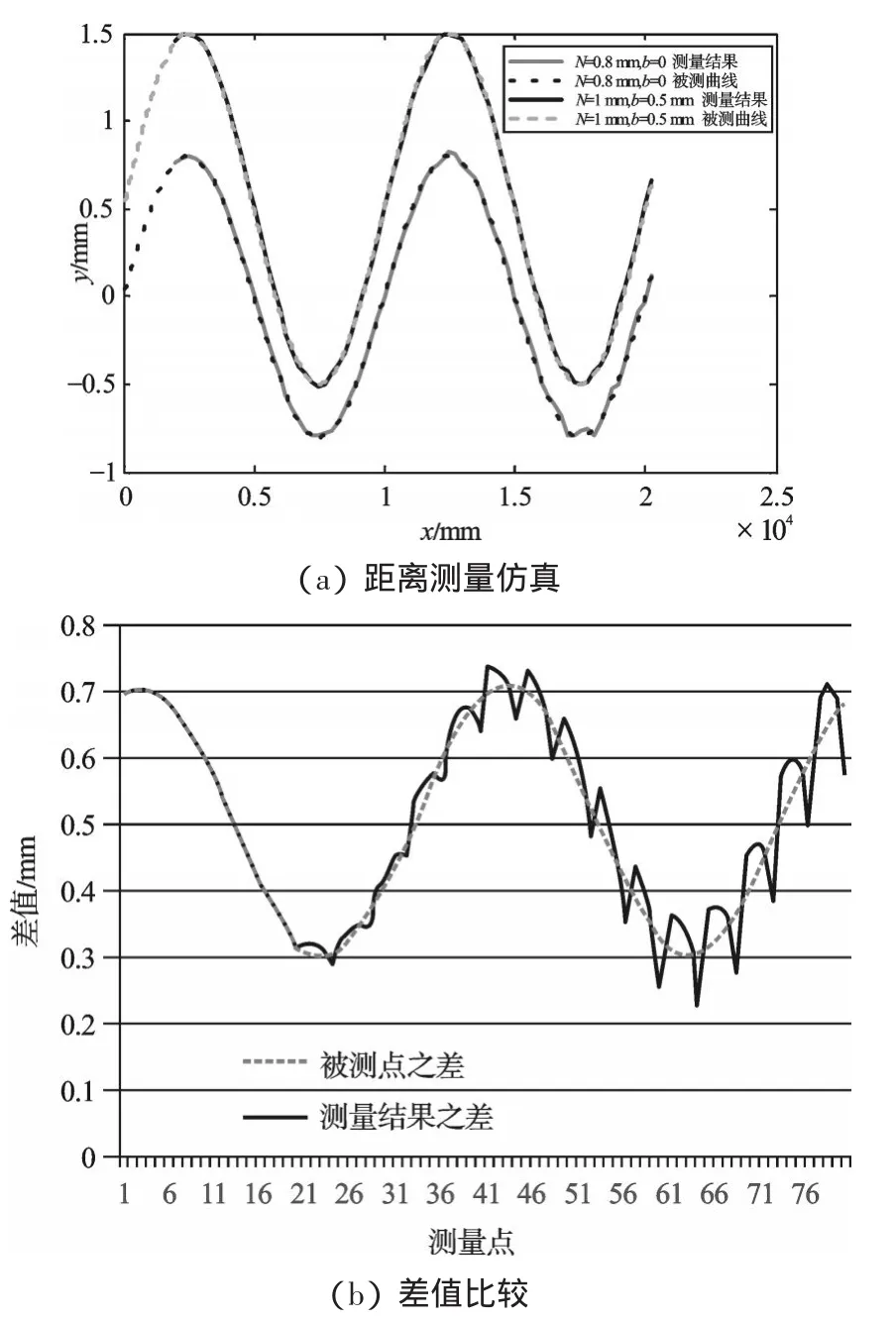
图6 打磨前后表面距离测量仿真
5 结束语
本研究针对高铁钢轨打磨砂轮的磨损问题,利用三点法测量原理、传感器测量误差、传感器安装误差、行走轮回转精度、测量方案进行了分析和Matlab仿真,建立了基于三点法的高铁钢轨打磨砂轮磨损的测量理论,可为测量小车的制作、测量方案的制定提供理论依据。
对钢轨打磨前后表面的测量结果表明,该方法满足了钢轨打磨过程中对砂轮磨损量的测量精度要求,为进一步研究测量高铁钢轨打磨砂轮测量方法提供了一种有效的方案,为钢轨打磨砂轮磨损的在线检测和实现砂轮磨损的补偿奠定了基础。
(References):
[1] 金学松,杜 星,郭 俊,等.钢轨打磨技术研究进展[J].西南交通大学学报,2010,44(5):1-11.
[2] 胡增荣.钢轨打磨列车在高铁上的应用[J].科技经济市场,2010(8):10-11.
[3] 杜 星,郭 俊,陈 婧,等.地铁线路控制钢轨波磨的钢轨打磨技术应用研究[J].机械,2011,38(10):9-13.
[4] [作者不详].中国铁路中长期发展规划[J].世界轨道交通,2008(9):66.
[5] 顾铁玲,王海丽,胡德金,等.基于计算机视觉的砂轮磨损状态的在线检测[J].机械科学与技术,2007,26(9):1147-1150.
[6] 宋贵亮,巩亚东,蔡光起.砂轮磨损状态的声发射检测及其误差补偿方法的研究[J].机械,2000,27(4):5-6.
[7] 李圣怡.精密超精密加工在线检测与误差分离技术[M].长沙:国防科技大学出版社,2007.
[8] 孙宝寿,詹圣望.三点法测量直线度误差应用研究[J].华东冶金学院学报,2000(7):217-220.
[9] 朱岱力,任成高,任 东.基于三点法检测深孔直线度的测量系统[J].装备制造技术,2009(11):79-81.
[10] 胡克佳,戴 勇,王华东,等.支持挤出平模头自动化研磨的测量技术[J].机电工程,2009,26(8):90-92.
[11] 冯骥飞,戴 勇,陈 硕,等.基于三点法的拟人化研磨测量仪器设计[J].机电工程,2010,27(8):69-72.
