基于遗传算法的关联规则挖掘

李广霞

（石家庄经济学院 信息工程学院，河北 石家庄 050031）

目前，关联规则挖掘算法一般是指Apriori算法或其改进算法［1］.其挖掘过程主要包含两个阶段：第一阶段必须先从数据集合中找出所有支持度大于用户最小支持度的项集的频繁项目集（Frequent Itemsets）；第二阶段由这些频繁项目集构造可信度大于用户最小可信度的关联规则 （Association Rules）.它实际上是一个全局搜索过程.遗传算法是一种全局优化算法，它可以有效地避免搜索过程的局部最优解问题，因此，将遗传算法用于关联规则的发现和提取有利于找到有价值的规则［2］.

1 遗传算法

遗传算法（Genetic Algorithms，简称GA）是模拟生物进化过程的计算模型，它是一种以自然选择和遗传理论为基础，将生物进化过程中适者生存规则与群内染色体的随机信息交换机制相结合的搜索算法［3］.

遗传算法不能直接处理问题空间的参数，必须把它们转换成遗传空间的由基因按一定结构组成的染色体或个体，这一转换操作叫做编码.编码有2种方式，即二进制编码和十进制编码.遗传算法的适应度函数也叫评价函数，是用来判断群体中个体的优劣程度的指标，它是根据所求问题的目标函数来进行评估的［4］，在使用时，需要随机产生一组规则，对每一个规则应用数据库中给定的例子进行判断，计算其适应度.先应用交叉运算和变异运算对该组规则进行优化，再利用选择运算产生下一代规则，从而实现优胜劣汰的进化过程.从优化搜索的角度而言，遗传操作可使问题的解一代又一代地优化，并逼近最优解［5］.

1.1 编码策略

编码是遗传算法中最基本的问题.对于规则项的编码方式分为二元编码和实值编码.

对于布尔型的关联规则挖掘可采取二元编码，但对不同类型的属性，编码方式并不相同.对于类别属性，如“婚姻状态”有四种取值：单身、离婚、已婚、丧偶，其编码长度为4，那么比特串0100代表的是离婚，0110代表离婚或者已婚；对于连续属性，一般先采用连续属性离散化，然后采用类别属性的编码方式.

对于非布尔型的关联规则挖掘可采取实值编码的方法.编码长度（数组中元素的个数）为n，A［1］存储项（属性）I1的值，A［2］存储项（属性）I2的值，以此类推，A［n］存储项（属性）In的值.这种编码方式简单且易于实现，便于遗传算子操作.在该方法中，需要对每个属性的所有取值进行分析：（1）若某个属性的取值是有限的、离散的，则将其从小到大定义为“值1”、“值2”……；否则，将那些连续的或者无限个数的取值划分为有限个取值区间，定义为“值1”、“值2”…….（2）若A［i］取值为k，则令A［i］＝k，若某个项集中没有包含属性Ii，则A［i］＝0.

1.2 种群初始化

遗传算法中初始群体的个体是随机产生的.初始群体的设定可采取如下策略：（1）根据问题固有的知识，设法把握最优解所占空间在整个问题空间中的分布范围，然后在此分布范围内设定初始群体.（2）先随机生成一定数目的个体，然后从中挑出最好的个体加到初始群体中.这种过程不断迭代，直到初始群体中个体数达到预先确定的规模.

对于二元编码的关联规则挖掘，随机生成N个n位由“0”和“1”组成的串作为初始种群；对于实值编码的关联规则挖掘，随机生成N个由“A［1］，A［2］，… ，A［n］”在定义范围内的值组成的串作为初始种群.

1.3 适应度函数

遗传算法在搜索进化过程中一般不需要其他的外部信息，仅用评估函数来评估个体或解的优劣，并作为以后遗传操作的依据.在具体应用中，适应度函数的设计要结合求解问题本身的要求而定.关联规则挖掘中频繁项集的衡量标准为支持度，它要求项集的支持度大于用户所给的最小支持度阈值（Min－Supp）.这是判断其是否为频繁项集的唯一标准.

因此，设计的适应度函数最好能分辨出支持度和MinSupp两者的大小关系.为此，定义群体中的个体X的适应度函数为：

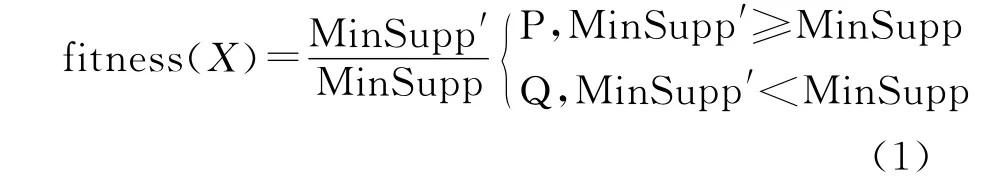
其中，MinSupp′表示个体X的支持度，当Min－Supp′大于MinSupp时，函数值大于1，此时个体X将在下一代中得以保存；否则，个体X将被淘汰.

1.4 遗传操作

遗传操作包括三个基本遗传算子（genetic operator）：选择（selection）、交叉（crossover）和变异（mutation）.

（1）选择算子

从群体中选择优胜的个体，淘汰劣质个体的操作叫选择.选择的目的是把优化的个体（或解）直接遗传到下一代或通过配对交叉产生新的个体再遗传到下一代.选择操作是建立在群体中个体的适应度评估基础上的.本文选择的操作是将适应度值大于1的规则留下来，并复制到下一代群体中.

（2）交叉算子

遗传算法中起核心作用的是遗传操作的交叉算子.所谓交叉是指把两个父代个体的部分结构加以替换重组而生成新个体的操作.交叉位置的选取是随机的.本文采用最简单的一点交叉.从交叉概率Pc在当前种群生成的交配池中随机选取两个个体X1和X2，随机确定交叉点，并将交叉点前后的部分进行交换，生成两个新的个体X1′和X2′，进入当前种群.

（3）变异算子

变异算子的基本内容是对群体中的个体串的某些基因座上的基因值作变动.由于遗传算法有局部搜索能力，引入变异可以提高群体中抗体的多样性并扩大搜索范围，从而搜索更优秀的抗体.根据关联规则挖掘的特点，变异概率Pm不是固定不变的.当种群中适应度小于1的个体数目M较大时，Pm取值较大；反之较小.Pm取值如下：

式中，α的值根据具体情况选取.

另外，参与变异操作的个体是在适应度值小于1的所有个体中随机选择的.

2 基于遗传算法的关联规则挖掘

2.1 算法

在关联规则挖掘的两个阶段中，将遗传算法的思想应用于频繁项集的生成过程中，从而实现对频繁项集的生成算法的改进.算法描述如下：

算法，基于遗传算法的关联规则算法（Genetic Algorithm for Association Rule）.

输入，事务数据库D，最小支持度MinSupp，种群规模n，交叉概率Pc，变异概率Pm，迭代次数T.

输出，D中频繁项集.

步骤1，初始化种群P0＝｛A1，A2，…，An｝，进行编码；

步骤2，计算P0中每个个体的适应度f（Ai）；步骤3，初始化后代种群Pi＋1，Pi＋1＝Ф；

步骤4，选择，若f（Ai）≥1，则 Pi＋1＝Pi＋1∪｛Ai｝，Pi＝Pi－｛Ai｝；

步骤5，交叉，从当前种群中随机选择两个个体A和B，按照给定的交叉概率Pc进行交叉，得到两个新个体A′和B′，则Pi＝Pi－｛A 和B｝，Pi＋1＝Pi＋1∪｛A′和B′｝；

步骤6，变异，随机从当前种群中选取m个个体，按照变异概率Pm进行编译操作，编译后产生的个体进入下一代种群Pi＋1；

步骤7，判断循环次数是否达到迭代次数T，如果达到，进入步骤8；如果种群Pi＋1中的个体数目Num小于n，则随机生成（n－Num）个个体进入种群Pi＋1，返回步骤2；

步骤8，输出结果；

步骤9，进行规则提取.

2.2 试验

为了比较Apriori算法和本文提出的基于遗传算法的关联规则算法的性能，设定数据库中的事务数为10 000，数据项集中的数据项个数为10，需要挖掘的关联规则最小置信度阈值为0.4，改变挖掘的最小支持度阈值，测试不同最小支持度阈值下的2种算法的运行时间，如图1所示.

试验表明，在相同数据规模下，不同支持度下的改进算法的执行时间比Apriori算法短.支持度越小，Apriori算法的执行时间越长，而改进的算法所需执行时间的增长速度低于Arpriori算法.

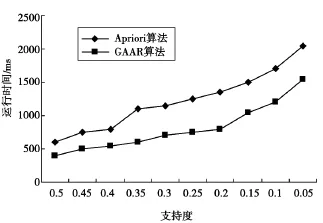
图1 不同支持度的运行时间比较图

3 结束语

本文分析了遗传算法在数据挖掘中应用的可能性，给出了基于遗传算法的关联规则算法，并从编码方法、适应度函数的构造、交叉算子和变异算子的设计方面进行了讨论和分析.最后试验表明，改进算法的执行效率高于Apriori算法.

［1］林倩瑜.关联规则挖掘算法研究综述 ［J］.软件导刊，2012，（6）：31－33.

［2］李阳阳，焦李成.求解SAT问题的量子免疫克隆算法 ［J］.计算机学报，2007，30（2）：176－183.

［3］符保龙.基于混合遗传克隆算法的关联规则挖掘 ［J］.计算机工程，2009，35（22）：216－218.

［4］STAKOVIE J.Misconceptions about Real－time Computing：a serious Problem for Next Generation System ［J］.IEEE Computer，1998，21（10）：10－19.

［5］AU W H，CHAN K C C，YAO X.A Novel Evolutionary Da－ta mining Algorithm with Applications to Churn Prediction［J］.IEEE Transactions on Evolutionary Computation，2003，7（6）：532－545.