塑料挤出机机筒壁厚设计的线性回归模型

金 琦，孙 竹

(南京艺工电工设备有限公司，江苏南京 211199)

塑料挤出机机筒壁厚设计的线性回归模型

金 琦，孙 竹

(南京艺工电工设备有限公司，江苏南京 211199)

基于力学理论和热平衡原理，建立了塑料挤出机机筒壁厚设计的线性回归模型，并从理论上论证了模型的合理性。利用一些成熟产品的设计给出了模型的解，且据此求得的产品设计参数与经验值高度吻合，明显改进了文献提供的参考值，表明模型在实践中是有效的。

塑料挤出机;机筒壁厚;强度设计;加热功率

挤出机机筒设计的关键是确定它的壁厚。过薄的机筒壁虽然温升快、质量轻，但因热容量小，故难于取得稳定的温度条件。反之，过厚的机筒壁不仅浪费材料，还使得机体结构笨重，升温慢，而且还会因热惯性大，导致温度调节滞后，影响性能。因此，合理的机筒壁厚是值得追求的。塑料挤出机机筒的壁厚取决于多方面的因素。除了满足足够的强度要求外，还必须符合塑化所需要的加热功率配置面积的要求。除此之外，还有许多无法量化的因素影响着壁厚的设计。甚至，壁厚的设计还必须考虑成型工艺条件所带来的影响。因此，经验在设计中起着重要作用。设计手册给出了机筒壁厚的推荐值范围，同时还给出了理论强度校核公式。但是按强度理论计算出的壁厚往往使机筒热惯性太小，由此得出的参数没有实际意义。市场上大多数挤出机机筒的实际壁厚远高于理论值，这些产品在具备良好的安全性的同时也满足了各种性能的要求。由于通过大量实验寻找最理想的设计参数是不经济、不现实的，经验对于机筒设计就非常关键，因此将既往成功设计的经验量化，使之成为新的设计的参考依据，具有明显的实际价值。本文的目的是根据力学原理和热学原理，综合考虑影响机筒壁厚的各种因素，建立数学模型，给出寻找有意义的壁厚参考值的方法。

1 挤出机机筒最大压力的确定

无论采用经验统计法还是强度校核法确定机筒壁厚，都必须首先求得机筒内的最大压力值。

1.1 挤出机机筒的结构及工作状态下的压力和温度

根据不同功能，挤出机机筒通常可以划分为如下几个部分:

a．加料段。工作时，塑料随着螺杆的旋转被向前输送，并通过机筒内壁和螺杆表面的摩擦被压实。塑料在加料段是以固体状态向前输送的。

b．熔融段。塑料被进一步压实和塑化，使包围在塑料内的空气压回到加料口排出，并改善塑料的热传导性能。这一段的螺槽是压缩型的。物料在该段呈固、液二相共存状态。

c．均化段。塑料进一步被塑化和均匀化，并被定压、定量和定温地从机头挤出。

在工作状态下，塑料在机筒内三段中的温度、压力和状态是变化的，其变化规律如图1所示。

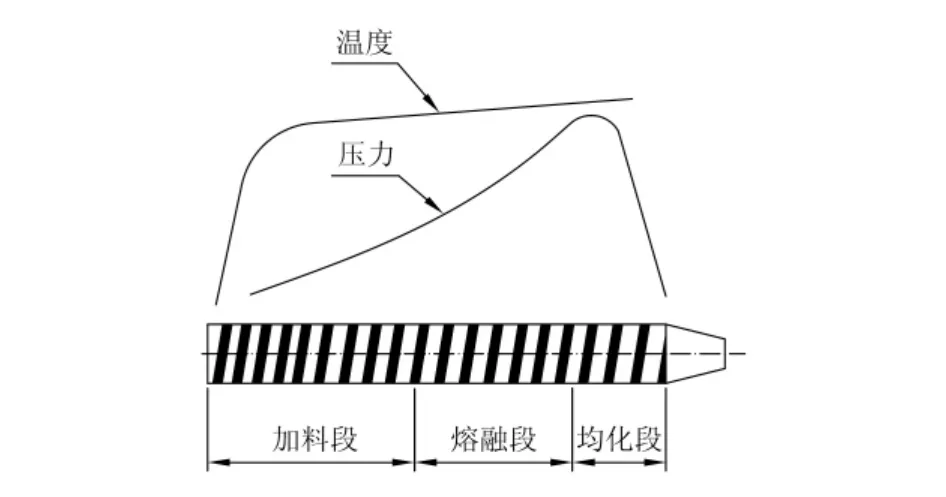
图1 挤出机过程温度和压力的变化

从图1可以看出，机筒内压力峰值在均化段末端出现，并延伸到机头。温度峰值是从加料段中间开始出现，平坦地延伸到机头。下面是用流体力学的分析方法，导出的应用于挤出机均化段流率的计算公式:式中:Q表示挤出机生产能力;D指螺杆直径;n指螺杆转速;h指螺杆均化段螺槽深度;φ指螺杆的螺旋升角;e指螺杆轴向螺棱宽度;Li指螺杆均化段长度;δ指螺杆与机筒之间径向间隙;E指螺杆偏心校正系数(通常取1．2);p指均化段末端压力;η1指螺槽中熔融物料粘度;η2指螺杆与机筒间隙中物料粘度。

1.2 机筒内最大压力值的确定

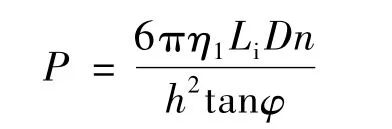
在式(1)右端的第一项是正流流率，第二项是压力流流率，第三项是漏流流率。当挤出机机头模板被异物堵塞、螺杆被熔融物料包住时，挤出机呈现断流挤出状态。此时，流率Q=0。如果把式(1)中第三项这一微量忽略不计，则可导出机头的最大压力理论值的计算公式:由此可以看出，机头压力 P 与 η1，Li，D，n成正比，与h2，tanφ成反比。此外，机头结构形式对机头压力有明显的影响。由图1的压力曲线可以看出，均化段末端的压力与机头压力相等。在公式(2)右端，除η1以外，其余各参数都由螺杆设计给出，因此只要测出η1的值，就可求得机头的最大压力(也即机筒最大压力)。

从图1还可以看出，机筒内各点物料沿螺杆轴线方向的压力值是不同的，其峰值出现在均化段末端与机头的连接处。对于同一种机头结构，在各种因素中，螺杆和机筒的结构对机头压力的影响最大，因此最大机头压力值即为机筒的设计压力值。用机头测压装置确定机筒内的最大压力值虽然很直观，但它毕竟不同于挤出机正常工作压力的测定，其测量是相当困难的。即使是同一台挤出机，在同一点、同一品种的物料，在不同时间测出来的数值也不会完全一致，会有波动。理论计算结果只能提供最大机头压力值的参考值，实际经验对最大机头压力值的确定也起着重要作用。

2 挤出机机筒的弹性应力学分析

2.1 机筒的受力分析

挤出机机筒属于两端开口的厚壁圆筒，但又不同于普通的厚壁圆筒，因为挤出机机筒还要考虑适应于塑化加热功率的配置要求。挤出机在挤出过程中，机筒内壁有高压熔体，使筒壁上任一点都处于应力状态，即周向应力σθ、径向应力σr和轴向应力σz，如图2所示。

图2 机筒壁厚上的应力分布

根据文献［1］，它们可以用下述公式计算:式中:pi，po分别指内压载荷及外压载荷;Ri，Ro分别指圆筒内半径及外半径;r表示圆筒壁内任一点半径。

对于挤出机机筒而言，仅有内压作用，即po=0。若记，则前述公式可以简化如下:

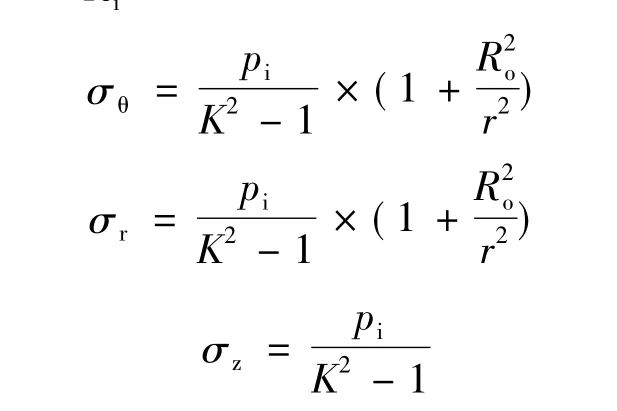
由此可以看出:(1)当r=Ri时，σθ为最大，最大值为(2)当r=Ri时，σr为最大，最大值为 －p;当r=Ro时，σr为最小，最小值为0。(3) 当 r=Ri时，σz=

以上分析表明，周向应力和轴向应力均为正值，是拉应力，径向应力为负值，是压应力。数值规律如图3所示。

图3 机筒受力断面图

由上述公式还可以知道:

a．机筒内壁周向应力σθ为所有应力中的最大值，其值为，内外壁所受压力之差为p;径向应力内壁为σr=－p，机筒外壁处σr=0。

应力沿壁厚的不均匀程度与径比K的值有关。以σθ为例，机筒内壁与外壁的，因此K的值愈大，应力不均匀程度也愈严重，当K的值接近1时，其比值接近1，此时机筒的周应力沿壁厚接近于均布。

以上分析还表明，机筒内壁径向应力最大并呈压应力。轴向应力σz沿机筒全长方向不变，而且其绝对值通常要比周向压力σθ小得多，所以机筒的强度主要是由σθ和σr决定的。

2.2 机筒的失效及强度计算

机筒设计应根据不同材料选用不同强度理论计算壁厚或进行校核。目前机筒多数采用弹性材料制造，因此可按第三或第四理论计算。通常采用的是第四理论及最大变形能量理论。

根据最大变形能量理论［2］，机筒强度条件为:

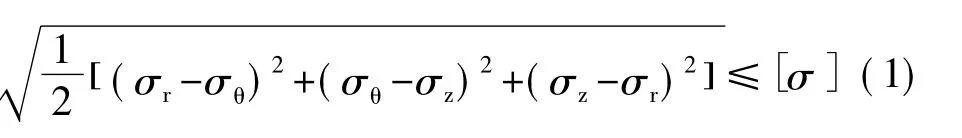
同样，将 σθ，σr，σz代入式(1) 得到机筒强度条件:。令机筒壁厚为δ，机筒内径为 D，则 D =D外－2δ，因此 δ=

3 挤出机机筒的热平衡分析

挤出机机筒壁厚设计不仅需要考虑机筒的疲劳强度性能，而且必须符合塑化所需的加热功率配置面积的要求。机筒的长度是已经确定的参数，外径是可变的。两者是确定机筒壁厚的主要因素，其他因素还包括机筒结构、挤出工艺等。

计算机筒加热功率的依据是塑化原理和塑化平衡原理。挤出过程中存在热平衡的问题。加热器供给的热能量和剪切摩擦能量是相互联系的，只要改变一种能量的供给速率，对另一种能量的需求就会发生变化。这是因为物料的温度升高时黏度就降低，它对螺杆的阻力就减小，剪切摩擦热也变小，即消耗电动机所供给螺杆的机械功就小;相反，若剪切摩擦愈强烈，即螺杆所供给物料的机械能量愈大，则物料从加热器所获取的能量就愈小。它们的相互关系如图4所示。

图4 挤出机热能供给情况

从图4中可看到，当螺杆达到一定转速时，物料所需要的热能将完全从螺杆转动的机械能获得，而不需要外部加热，这就是所谓“自然挤出”。图中第二组曲线与横坐标的交点A和B就是自然点。加热器供给的热量和因摩擦剪切而产生的热量部分地用于使塑料产生物态的变化，另一部分是损失掉的。损失的这部分包括机筒机头和周围介质的热交换、冷却介质带走的热量以及加热元件本身的热量损失和制品带走的热量。有如下热平衡方程式:

式中:H外热是加热系统所供给的能量;H内热表示传动系统的机械能通过螺杆对塑料的挤压、剪切和摩擦等而转换成的能量;H塑化表示塑料在挤出过程中所得到的热能;H损失表示塑料在挤出过程中的热损失。

挤出机的加热功率虽然可以用式(2)表示，但因为影响热平衡的因素很多，所以目前塑料挤出机机筒加热功率为

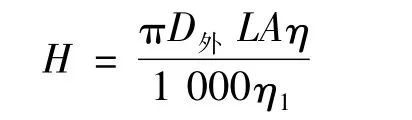
式中:H是机筒加热功率，kW;L指机筒加热部分的长度，cm;A表示单位面积加热功率，W/cm2。A值根据经验决定，一般取A≈4W/cm2。如果以D外表示机筒外径(cm)，η1表示加热器加热效率，η表示加热器有效加热面积效率，则有 D外=

4 计算壁厚的线性回归模型

机筒失效强度及机筒塑化所需的加热功率配置面积是机筒壁厚设计最重要的理论根据。此外，诸如机头的结构、材料的性能、工艺方法等不易量化的因素也影响到机筒的厚度。设计教科书均会提供各种型号挤出机机筒壁厚参数的推荐值。出于安全考虑，多数推荐值过大，以此生产的机筒壁厚太厚，既费材料，加热时间且长，很不经济。因此，这些推荐值均有较大的修正余地。

企业通过强度试验确定机筒壁厚是不现实的，多数机筒壁厚的设计参数都是凭经验确定的，因而设计者的个人判断就极其重要，常常不免带有明显的主观色彩。

为了尽可能减少每次设计中主观因素的影响，根据最大变形能量理论、热平衡原理，下面建立确定壁厚参数的线性回归模型。

用δ1表示根据最大变形能量理论得出的机筒壁厚度，用δ2表示根据机筒塑化所需的加热功率配置面积得出的机筒壁厚度。假设实际机筒壁厚是δ1和 δ2的线性函数:

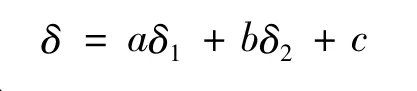
其中:a，b≥0。

这样的假设是合理的。由于δ1和δ2是影响机筒壁厚的最重要的参数，可以认为，机筒壁厚是关于δ1和δ2的光滑函数。从数学分析的角度来讲，足够光滑的函数一定可以展开成自变量的泰勒级数。如果将高阶项舍掉，就可以将之近似地看作是关于自变量的线性函数。其中a，b≥0的要求表示理论值与实际设计参数的正相关性，c也具有明确的物理含义，即表示其他因素对于壁厚参数的影响。因此，建立壁厚参数的数学模型如下:

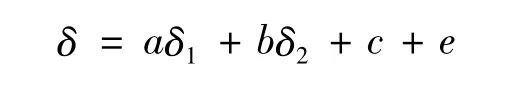
其中:a，b≥0。

这一模型以机筒壁厚设计的力学原理和热平衡原理为依据，将专家以及既往成功设计的经验量化，为以后挤出机机筒壁厚的设计提供有意义的参照。实践表明，根据这一模型获得的机筒壁厚比教课书上提供的推荐值更经济、更合理，更具参考意义。

以SJ－150×25单螺杆挤出机为例来说明如何校核机筒壁厚。先利用数学模型分析计算，并考虑结构、材料、工艺等各方面的因素进行修正，最终确定机筒壁厚参数。实践表明，这样的的设计完全符合实际要求。表1中的数据是已有机型相关参数。多年的生产经验及实际使用效果表明，这些机型机筒壁厚的设计完全符合生产和使用的要求，从来没有因为壁厚的变薄而发生任何安全问题和热容量不够等现象。因此可以认为，这些设计都是成功的，相关参数可以作为未来设计参数的参考依据。

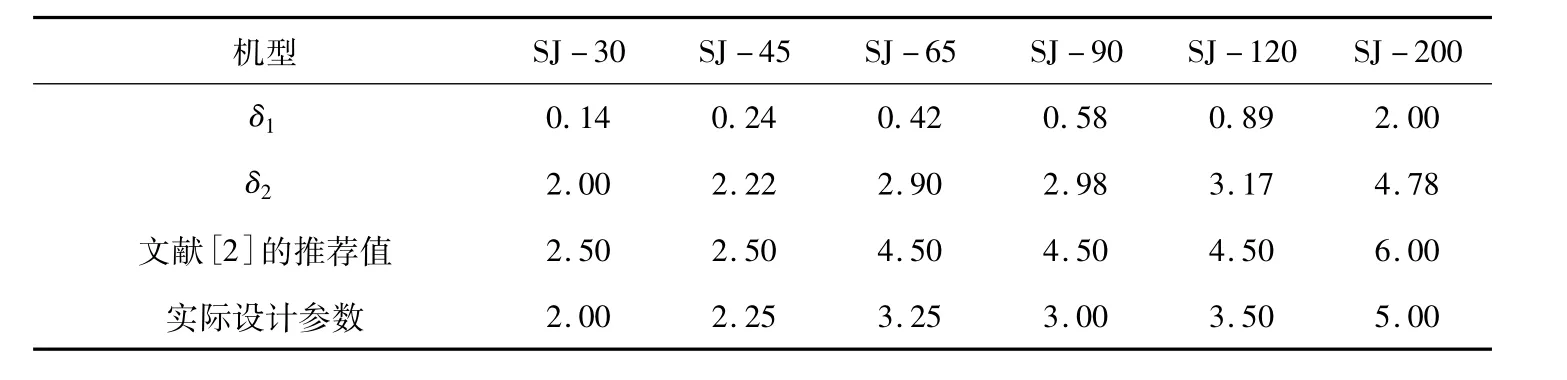
表1 挤出机机筒壁厚对比表 cm

从表中数据可以看出，表中所列各种不同机型壁厚均符合力学原理和热平衡原理的要求，但实际参数往往比推荐值小很多。

根据最小二乘法的原理及上述数据以及LINGO 软件，求得模型参数 a=0，b=1．209 7，c=－0．420 1。计算结果显示，均方差为0.044 1。因此，这一模型是可以接受的。

SJ－150×25单螺杆挤出机的机筒加热功率H=88.2kW，机筒加热长度L=279cm，许用应力［σ］=2.77×104N，机头最高压力 p=4.41×103N，机筒内径D=15cm，加热器加热效率η1=0.7，加热器有效加热面积效率η=0.95。经计算得δ1=1.30cm，δ2=3.28cm。由模型计算得δ=3.547 71cm。用模型计算所得的机筒壁厚完全符合强度理论和热平衡理论的要求，并且与经验值高度吻合。综合各种因素，SJ－150×25单螺杆挤出机的机筒的实际壁厚确定为3.05cm，比教材推荐值4.50cm小了1cm。实际使用结果表明，这款机型机筒壁厚完全符合生产的安全要求。

5 结束语

上述例子中参数a=0的结果完全符合直观的预想，因为在大部分情形下，机筒壁厚的设计中，热平衡原理的要求是决定性的，凡符合热平衡原理要求的壁厚一定符合机筒失效强度的要求，所以挤出机机筒加热功率设计必须建立在塑料塑化所需热能的基础上，而不是根据机械强度设计的机筒的表面积去考虑设计加热功率。在这一点上，数学分析的结果与经验判断是一致的。

由于材料疲劳强度的复杂性，以及新工艺、新材料、新技术的应用使得难以给出一个普遍适用的设计准则，对目前的设计准则也很难作出绝对正确的检验。如果单凭经验或类比的办法确定相关参数，则难免会因个人的主观臆断而产生设计上的偏差。上述模型提供了将经验量化的方法，从而可以有效减少设计的盲目性。实践证明，用这种方法最终确定机筒壁厚是可行的。量化的模型则可以提供相对来说既经济且安全的参考。从这个意义上讲，不论模型是否最优，这一想法是有意义的。

［1］李志义，丁信伟.厚壁圆筒形构件的疲劳性能［J］.化工装备技术，1996(4):41－46.

［2］北京化工学院，华南工学院.塑料机械设计［M］.北京:中国轻工业出版社，1994.

The Linear Regression Models for Barrel Wall Thickness Design of Plastic Extruder

JIN Qi，SUN Zhu
(Nanjing Yigong Electrical Equipment Co.，Ltd.，Jiangsu Nanjing，211199，China)

Based on the mechanical theory and the principal of thermal equilibrium，it establishes a mathematical model for the barrel wall thickness design of the plastic extruder，proves the rationality of the model mathematically.According to parameters in the designs of some successful products，it obtains the solution of the mode，the design parameters includes the empirical value.The result improves considerably the reference value provided by the literature.This illustrates the validity of the model in practice.

Plastic Extruder;Barrel Wall Thickness;Strength Design;Heating Power

TH12

B

2095－509X(2013)11－0097－05

10.3969/j.issn.2095－509X.2013.11.025

2013－09－18

金琦(1963—)，女，江苏南京人，南京艺工电工设备有限公司工程师，主要从事电工机械设计工作。