广义测不准关系对无限深势阱问题的影响

马孟森，李怀繁，赵惠华

（山西大同大学物理与电子科学学院，山西 大同 037009）

广义测不准关系对无限深势阱问题的影响

马孟森，李怀繁，赵惠华

（山西大同大学物理与电子科学学院，山西 大同 037009）

考虑了广义测不准原理，并重新计算无限深势阱问题，得到能量本征值。结果表明，此时的能量本征值除了包含通常的En=h2π2n2/2ma2以外，还包含能量修正项。而且能量本征值修正项只与参数α有关，与其它的参数没有关系。

广义测不准关系；无限深势阱

1 引言

自从20世纪30年代人们就已经知道位置和动量之间的测不准关系的存在，[x^，p^]=iħ或者ΔxΔp≥ħ/2。根据坐标算符和动量算符可以构成一些其他量子算符。但是近年来随着量子引力理论的发展，特别是在弦论和圈量子引力理论中都预言“最小尺度”的存在[1]。而这个所谓的“最小尺度”可能正是来自于广义测不准关系[2-3]。这也开辟了一个很有意思的研究方向。

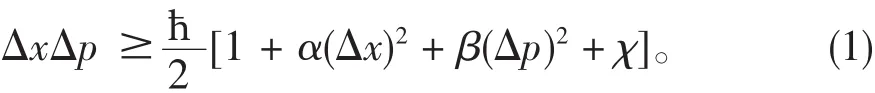
最完整的广义测不准关系是[4-6]：考虑一种特殊情况[7-9]：α=χ=0，此时上式化为一个简单的形式：

或者

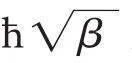
本文考虑β=0的特殊情况，此时在位置表象下，满足方程（1）的坐标和动量算符可表示为：因此，

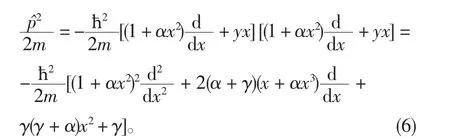
2 无限深势阱

当x∉（0，a）时有Ψ（x）=0，特别是在边界上有Ψ（0）=Ψ（a）=0。当x∈（0，a）时，薛定谔方程变为宽为a的一维无限深势阱有即做变量代换，令方程（9）变成

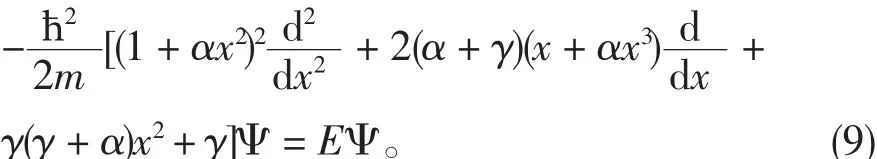
其中，ε＝2mE蛐ħ2α，Δ＝γ蛐α。注意这里的波函数＝（ρ）。

从方程（11）可以看出，若γ=0，则方程化为通常的一维无限深势阱的波动方程，只是这里的变量是ρ而不是x。因为γ是任意的，所以物理量应该不依赖于γ的值。事实上，可以通过计算证明γ=0和γ≠0给出同样的能量本征值。下面只给出γ=0的结果，更一般的情况笔者另文论述。此时方程为该方程有通解为其中，C1，δ是两个积分常数。在新坐标下边界为ρ=0和ρ=ρa=arctana，在边界上有（0）＝（ρa）＝0。据此可推得δ=0以及故能量本征值为

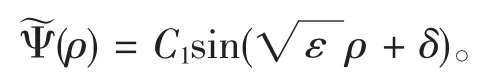
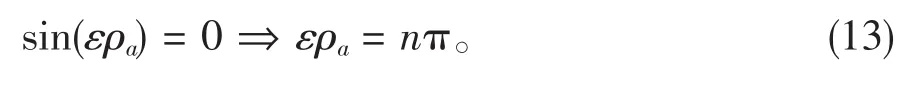
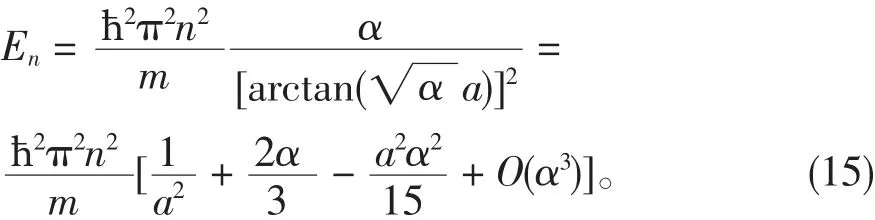
把ρa=arctana代入上式并做泰勒级数展开，可得显然，该结果首要项即为通常的一维无限深势阱的能量本征值，修正项都依赖于α。所以，如果α=0，则由广义测不准关系得到的能量本征值就回到了通常的结果。

3 结论

根据广义测不准关系，得到修正的一维无限深势阱问题的能量本征值。结果表明，存在与α相关的能量修正项，而与其它参数没有关系。虽然无限深势阱是一种理想情况，但是对这种理想问题的研究既可以反映出广义测不准原理的特点，而且该研究方法还可以推广到其他情况，如有限深势阱以及线性谐振子等问题。无论如何，广义测不准关系是否成立及其参数的值都需要在将来的量子力学实验中进行验证。

[1]AmatiD，CiafaloniM，Veneziano G.Can spacetime be probed below the string size[J].Phys Lett B，1989 226：41.

[2]Konishi K，PaffutiG，Provero P.Minimum physical length and the generalized uncertainty principle in string theory[J].Phys Lett B，1990，234：276-284.

[3]Maggiore M.Quantum groups，gravity，and the generalized uncertainty principle[J].Phys Rev D，1994，49：5182-5187.

[4]Kempf A，Mangano G，Mann R B.Hilbert space representation of theminimal length uncertainty relation[J].Phys Rev D，1995，52：1108-1118.

[5]Kempf A.Uncertainty relation in quantum mechanicswith quantum group symmetry[J].JMath Phys，1994，35：4483-4496.

[6]NozariK，Pedram P，Molkara M.Minimal length，maximalmomentum and the entropic force law[J].Int JTheor Phys，2012，51：1268-1275.

[7]Chang L N，Minic D，Okamura N，et al.Takeuchi，Exact solution of the harmonic oscillator in arbitrary dimensions with minimal length uncertainty relations[J].Phys Rev D，2002，65：125027.

[8]Medved A JM，Vagenas E C.When conceptual worlds collide-The generalized uncertainty principle and the Bekenstein-Hawking entropy[J].Phys Rev D，2004，70：124021.

[9]Zhao R，Wu Y Q，Zhang L C.Generalized uncertainty principle and thermodynamic quantities of the Achucarro-Ortiz b lack hole [J].Mod Phys Lett A，2008，23：839-846.

〔责任编辑 李 海〕

Generalized U ncertainty P rincip le and its E ffect on S quare W ell

MA Meng-sen，LIHuai-fan，ZHAO Hui-hua

（School of Physical Science and Electronics，ShanxiDatong University，Datong Shanxi，037009）

In this paper we considered the generalized uncertainty principle and recalculated the infinite potential square well to obtain the energy eigenvalue.It show s that the energy eigenvalue is different from the usual result En＝h2π2n2蛐2ma2because of the existence of some correction terms.Moreover，the correction terms are only relevant to the parameterα.

generalized uncertainty principle；infinite potential squarewell

O411.1

A

2012-10-10

国家自然科学基金理论物理专项[11247261]；国家自然科学基金项目[11075098，11175109]；山西大同大学博士科研启动经费[2011-B-03]；

马孟森（1984-），男，河北沧州人，博士，讲师，研究方向：引力理论、黑洞物理、宇宙学。

1674－0874（2013）01－0030－04