四元数在计算机辅助手术空间配准中的研究*

韦韫韬，周轶冰，周东航，李春洁

(1.佳木斯大学，佳木斯 154007;2.佳木斯市中心医院，佳木斯 154002)

1 前言

1843年，英国数学家哈密尔顿(W.R.Hamilton 1805－1865)发现了一种数学概念—四元数，它的乘法不符合交换律，是一种非常简单的超复数，作为对复数的一种扩充，强有力地推动了向量代数的发展。近些年，研究者发现四元数可以用来表示物体的旋转特性，同时也开始应用于计算机辅助外科手术的空间配准技术上［1］。

2 四元数及其在三维空间的应用

四元数由一个实部和三个虚部组成，表示为:r=r0+r1i+r2j+r3k。其中r02+r12+r22+r32=1，另外，四元数不符合乘法交换律，打破了固有的乘法概念，四元数的乘法规则见表1。

表1 四元数乘法运算表

由于四元数乘法存在上述的特殊性，例如:i*j=－(j*i)，所以正好可以使用四元数来表示三维空间中物体的旋转和平移，使用以下矩阵形式来表示三维空间中的任意一点。

可以将该矩阵分成两部分:①对角线上的元素(a11，a22，a33)用于表示不同空间尺度的变换;②除对角线以外的其他元素用于表示两个空间转换时的旋转矩阵。如果只考虑第二部分，即不考虑两空间的尺度变换，则四元数就完全可以用来表示两空间点集配准时的旋转矩阵［2］，借助四元数旋转矩阵可以表示为:

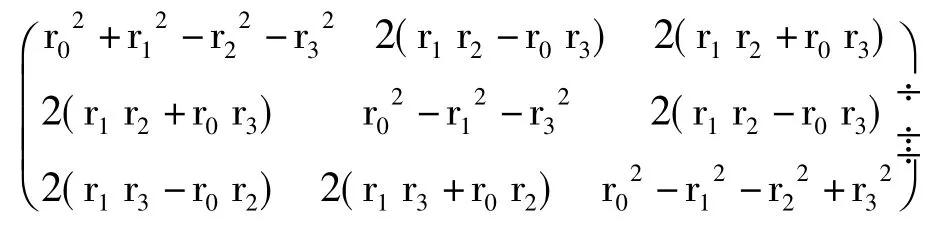
3 基于点集的空间配准方案

3.1 算法基本原理

假设 P、Q 两个空间点集，其中 P={pi，i=1，2，…，n}表示在坐标空间(x，y，z)下的图像空间点集，Q={qi，i=1，2，…，n}表示在坐标空间(u，v，w)下的手术空间点集，两坐标空间下P和Q中的点一一对应。找出医学图像空间和手术空间两点集的对应关系和转换规则是基于点集的控件配准算法的主要研究内容。可以使用一个旋转矩阵和一个平移向量来表示两空间点集的转换和配准，即两点集之间的线性关系如下:

其中，R代表配准过程中所需要的旋转矩阵，T代表平移向量，ε则是进行两空间点集配准时所产生的误差项［3］。如果配准后，ε在可以接受的范围内，R和T则是要寻找的最优旋转矩阵和最优平移向量，于是如何控制ε在可接受的范围内就成为了要解决的重要问题。由于两空间点集中包含的点很多，令pi和qi为任意一对对应点，对其进行空间配准时一定会产生一个相对应的误差项εi，利用最小化误差平方和的原理就可以解决控制误差的难题，即满足:

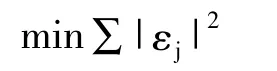
具体采用以下方法:首先进行数据采集，获取实验模型的特征点数据，利用三维坐标和四元数来表示这些特征点的信息;然后计算点集的质心和点集的协方差矩阵，构造特征矩阵，经过雅可比变换找到最大特征值和相应的特征向量;最后利用最小化误差平方和的原理获取最优旋转矩阵R和最优平移向量T，以达到医学图像空间和手术空间的精确配准［4］，流程如图1 所示。

3.2 空间配准的矩阵求解

(1)已知两个空间点集 P={pi，i=1，2，…，n}，Q={qi，i=1，2，…，n}，利用统计学均值表示两点集质心分别为:

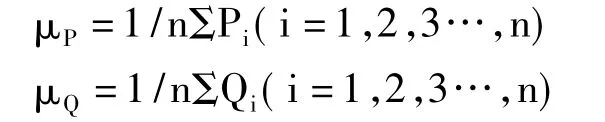
(2)计算两点集的协方差矩阵为:

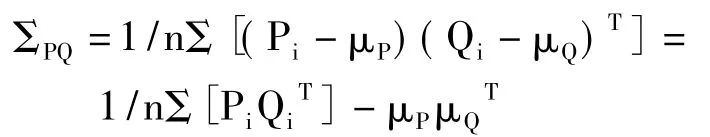
图1 空间配准算法流程图

(3)假设协方差矩阵为:

(4)构造特征矩阵

选取Σ的元素组成列向量W=［E23E31E12］T，则可得到对称矩阵:

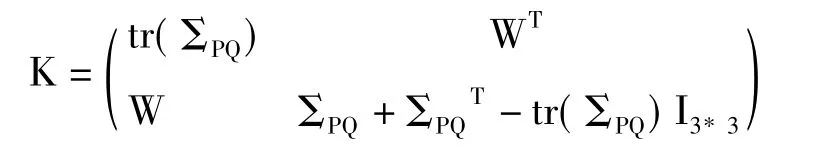
(5)利用矩阵变换理论，对K进行雅可比变换，得到矩阵K的最大特征值和相应的特征向量为［r0r1r2r3］T作为最优的旋转向量，通过计算可得r02+r12+r22+r32=1，则为满足条件的四元数。可以计算最优旋转矩阵R，再计算最优平移向量T为:

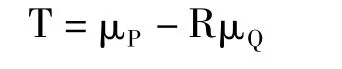
4 选取仿真实验的特征点

本次仿真模拟实验中模型特征点的获取采用了标志点法，这主要是因为:①考虑到仿真实验中，标志点法的可操作性强，实现比较容易;②标志点法获取的特征点数据比较精准。但实际操作中也要注意，实验模型做完CT扫描后，标注点的位置不能改变，否则将会严重影响仿真实验的精准性［5］。

5 仿真实验结果及分析

本次模拟仿真实验采用肝脏模型作为实验对象，实验前对模型进行CT扫描，采集了4个标志点作为配准仿真实验的对象。首先记录实验前模型空间4个标志点的三维坐标，见表2。

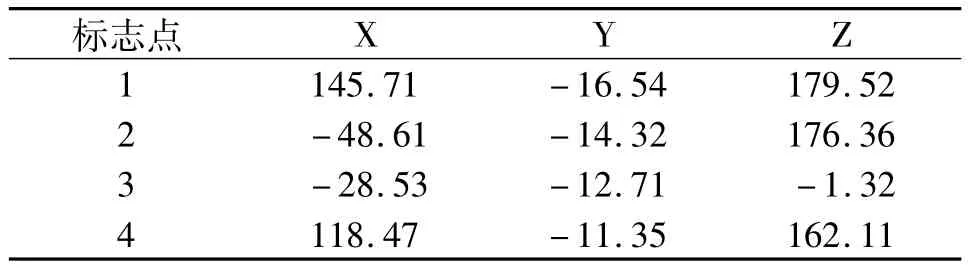
表2 配准前CT图像空间标志点坐标

同时记录仿真实验前模型空间4个标志点的三维坐标，见表3，两组点集一一对应。

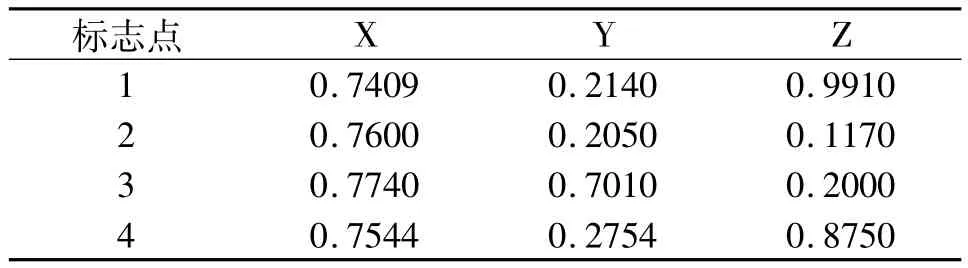
表3 配准前模型空间标志点坐标

由于两点集所在空间不同，需要进行尺度变换，然后进行空间配准，空间配准的尺度、四元数和平移向量都是满足最小化误差平方和的最优解［6］。同时可以获得坐标变换矩阵，计算出配准后模型空间点集的三维坐标如表4所示。

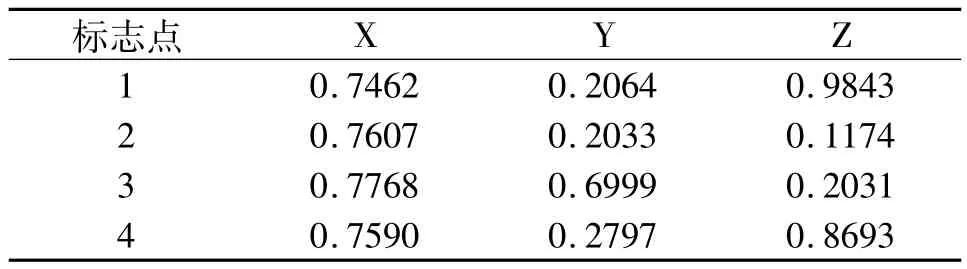
表4 配准后模型空间点集坐标

由各表中的三维坐标可以看出，本次仿真实验有效的控制了空间配准的误差，ε＜0.5mm，在可以接受的范围内。

6 结 束 语

利用四元数矩阵分解方法详细地推导了空间配准算法的原理和矩阵求解过程，并利用最小化误差平方和方法获取了三维医学图像空间和手术空间配准时的最优旋转矩阵和最优平移向量，成功地解决了计算机辅助肝脏手术中空间配准这一关键技术。

［1］Grimson W，Eric L，Kikinis R.Image－guided surgery［J］.Scientific American，1999，24(6):62 －69.

［2］Peters T M.Image－guided surgery and therapy:current status and future directions［A］.Proceedings of SPIE The Inter national Society for Optical Engineering［C］.London:The MUT Press，2001:1 －12.

［3］Gunkel A R，Thunmfart W F，Freysinger W.Computer aided 3 － navigation systems［J］.Survey and location determination，2000，48(3):75 －90.

［4］Hassenpflug，Peter.Superiority of auto － stereoscopic visualization for image－guided navigation in liver surgery［A］.Proceedings of SPI E［C］.London:The MUT Press，2002:24－26.

［5］王勇，马立元，王忠强.四元数法在计算机图形学中的应用［J］.军械工程学院学报，2001，13(2):48 －51.

［6］张铁，谢存禧.机器人学［M］.广州:华南理工大学出版社，2001:123－139.