用流态化理论分析气体钻井携岩问题
2013-09-12王朝飞朱忠喜吴继伟雷先志
王朝飞 朱忠喜 吴继伟 雷先志
(1.长江大学(武汉校区)石油工程学院,湖北 武汉 430100;2.中国石油新疆油田公司工程技术处,新疆 克拉玛依 834000;3.中国石油新疆油田公司工程技术研究院,新疆 克拉玛依 834000;4.中国石油塔西南勘探开发公司柯克亚作业区,新疆 库尔勒 844804)
0 引言
气体钻井具有提高机械钻速、克服井漏、防止水敏性地层井壁坍塌等优点,越来越受到钻井业界人士的关注。在气体钻井施工中保持充足的气体流量对成功实施钻井至关重要。目前,对满足井眼净化条件下最小注气量问题的研究文献中,介绍较多的研究方法有两种:一是从空气采矿钻井实践中得到的经验型最小动能法,二是从气固两相流中的颗粒运动学角度出发得到的最小速度法[1]。前者工程实用性较强,后者更侧重于研究岩屑运移内部机理[2-3]。笔者着重从岩屑运移的本质出发,结合冶金和化工等领域中的“流态化理论”[4],研究气体钻井岩屑运移机理。
1 固体流态化过程
流态化简单来说就是固体物质流体化,是指流体(气体或液体)以一定的流速通过固体颗粒组成的床层时,可将大量固体颗粒悬浮于流动的流体中,颗粒在流体作用下上下翻滚,犹如液体,在流体中跳跃或随流体一起流动的状态。当流体自下而上流过颗粒组成的床层时,因流体流速不同会出现不同的情况,随着流体流速的逐渐增大,相继会出现:固定床阶段、床层膨胀阶段、全部颗粒都悬浮阶段、输送床阶段。在每个阶段中,固体颗粒的运动状态发生变化的原因是由于受流体流速影响显著的曳力发生了变化。
2 曳力分析
流体以一定的速度绕过颗粒流动时,流体与颗粒之间产生一对大小相等、方向相反的作用力,将流体作用于颗粒上的力称为曳力。当流体自下而上流过颗粒组成的床层时,随着流体流速的逐渐增大,固体颗粒所受曳力变化显著,曳力与流体的流速、物性以及颗粒性质之间的关系[5]如图1所示。
颗粒微元面积d S上的曳力为:
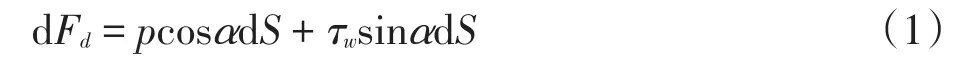
式中,Fd为颗粒所受的总曳力,N;p为压力,MPa;τw为剪应力,N/m2;α为流速与壁面法向夹角,(°);S为颗粒表面积,m2。
将上式沿颗粒表面积分,得到总曳力为:
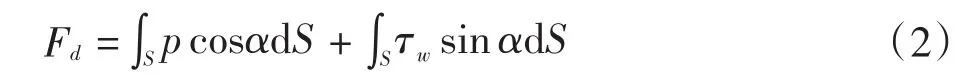
对于光滑球体颗粒,利用因次分析方法,可得出曳力表达式为:

式中,CD为曳力系数,与雷诺数Re=有关;Ap为颗粒在流动方向上的投影面积,m2;ρg为流体密度,kg/m3;v为流速,m/s。

图1 作用于颗粒上的形体曳力和表面曳力图
3 井筒中岩屑运移受力分析
假设井筒中某点处球形岩屑颗粒受到重力G、浮力Fb和曳力Fd3个力的作用,如图2a所示。

图2 岩屑受力分析图
根据牛顿第二定律,具体表示为:

式中,ρs为颗粒的密度,kg/m3;g为重力加速度,m/s2;dP为颗粒直径,m;a为加速度,m/s2。
由于曳力随气流速度增大而增大,当气流速度较小时,悬浮的岩屑颗粒受到的曳力小于岩屑的浮重,岩屑具有向下的加速度而有回落到井底的趋势;当气流速度大到足以克服浮重的影响时,岩屑具有向上的加速度,岩屑开始向上移动。在气流速度v增大的过程中必然存在某一数值vt(临界流速),此时阻力、浮力与重力三者的合力为零,颗粒处于悬浮状态。在气体钻井条件下,需对曳力系数进行修正,其临界流速vt表示为:

式中,vt为临界流速,m/s;∅s为球形度。
以上计算是根据均匀上升气流中岩屑颗粒受力分析得出的临界流速,而当环空当量直径与岩屑颗粒平均直径的比值(db-dc)/dP<100时,还应考虑岩屑上移受到井壁和钻柱壁面的限制的情况。岩屑颗粒与颗粒、颗粒与边壁在发生碰撞过程中会发生能量损耗,相当于岩屑在上升过程中又受到了一个向下的阻力作用,即边壁效应。边壁效应产生的阻力为Fr,如图2b。引入Zenz.F.A和D.F.Othmer对边壁效应的影响修正系数[4-5],可得出:
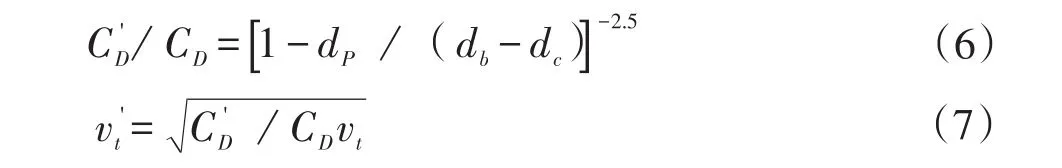
在气体钻井条件下,岩屑颗粒并非圆球状,颗粒形状对曳力系数是有影响的,因此,还要对上述公式进行修正。
4 井眼净化条件
当岩屑颗粒群一起向上移动时,岩屑之间还存在着相互作用。Bradshaw认为,当岩屑组分等体积分数Cp低于0.04时,岩屑颗粒的相互作用较弱,可以忽略[6]。因此,根据这个原则确定机械钻速条件下的岩屑当地上移速度vtr,即相对井壁的岩屑上移速度。其计算公式如下:
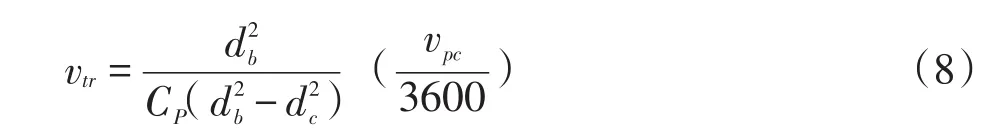
岩屑能够被气流顺利携带上移,满足井眼净化条件的气体流量为:

式中,vtr为岩屑当地上移速度,m/s;CP为体积分数;qg为气体体积流量,m3/s;vPC为机械钻速,m/h。
以上分析都是在井眼中任一点处进行的,气体密度和黏度大小都是指该点处的压力和温度的数值。因此,在进行气体体积流量计算时还应对井筒压力进行迭代求解。
5 实例计算
结合文献6中给出的伊朗SNL-7井空气钻井实钻参数,应用文中的流态化理论模型,计算了第三次开钻和第四次开钻的注气量,计算结果及误差对比如表1所示。
与文献6提供相同计算条件下的计算结果相比,应用文中颗粒运动临界流速法计算得到的结果比实钻数据要小,误差在-10%以内,更加接近实钻情况。

表1 计算结果及误差对比情况表
6 结论
1)应用流态化颗粒运动理论分析气体钻井携岩规律时,所得到的曳力修正系数是受气体速度、环空边壁效应、颗粒大小、球形度影响的多元函数,而不能被简单地归结为某一常数值。
2)环空当量直径和岩屑颗粒直径的比值越大,其边壁效应越强烈,则满足携岩条件的气体流速或气体流量越大。
3)颗粒越接近球形,其曳力系数越小,满足携岩的气体流速越大;反之,颗粒越不规则,其曳力系数越大,满足携岩的气体流速越小。
4)采用修正后流态化气体携岩模型计算得到的结果更接近现场实际,模型更加可靠。
[1]Boyun Guo,Ali Ghalambor.欠平衡钻井气体体积流量的计算[M].北京:中国石化出版社,2006.
[2]孟英峰,练章华,李永杰,等.气体钻水平井的携岩研究及在白浅111H井的应用[J].天然气工业,2005,25(8):50-53.
[3]郭建华,李黔,王锦,等.气体钻井岩屑运移机理研究[J].天然气工业,2006,26(6):66-67.
[4]吴占松,马润田,汪展文.流态化技术基础及应用[M].北京:化学工业出版社,2006.
[5]曾凡,胡永平,杨毅,等.矿物加工颗粒学[M].徐州:中国矿业大学出版社,2001.
[6]岳国林,杨万和,郑传义.空气泡沫钻井技术在伊朗SNL_7井的应用[J]. 新疆石油科技,2007,17(4):1-4.
