基于开放式数控系统的零相差跟踪控制*

李学伟，赵万华，卢秉恒

(西安交通大学机械制造系统工程国家重点实验室，西安 710054)

0 引言

数控机床进给系统的动态特性，导致实际加工过程中系统输入与输出间存在变化的跟随误差。进给系统的跟踪性能直接影响数控机床的加工精度［1］。Tomizuka［2］提 出 的 零 相 差 跟 踪 控 制 (zero phase error tracking controller-ZPETC)是一种基于逆系统思想的控制方法，即设计控制器为控制对象的逆，结合零极点对消和相位对消，使得控制器和被控对象的串联传递函数近似为1，在较大的带宽范围减少传统反馈闭环系统所带来的相位误差和幅值误差，达到更高的跟随精度。

由于零相差控制能够有效改善机床进给系统的跟随特性，提高数控机床的加工精度，国内外学者相继提出了最优增益零相差和自适应零相差跟踪前馈补偿方法，并对其进行了大量改进研究和应用［3-11］。最优增益零相差跟踪控制主要用于提高进给系统的中高频幅频特性，前馈控制器设计相对复杂。自适应零相差跟踪控制虽然对进给系统负载变引起的系统特性变化具有一定的自适应调节能力，但需要实时对系统模型进行在线辨识，而系统模型辨识的实时性和准确性使该方法的应用受到很大限制。与最优增益零相差和自适应零相差跟踪控制相比，零相差跟踪算法相对简单并能保证系统具有较好的稳定性。对于传统的数控机床，由于数控系统是封闭的，该方法一直处于实验室研究和实验阶段，无法在其内部实现零相位跟踪控制算法。

本文以RTX660数控铣床为研究对象，利用PA数控系统的二次开发功能，将零相差跟踪控制算法嵌入到数控系统插补器中提高了数控机床的单轴运动控制精度，同时减小了多轴联动加工的轮廓误差。

1 进给系统模型辨识

进给系统的模型辨识有开环系统模型辨识和闭环系统模型辨识［12］。因为插补器位于位置闭环以外，本文选择利用伪噪声序列对进给系统进行开环系统模型辨识。

1.1 伪噪声序列的产生

本文采用线性同余法［9］产生系统辨识所需的伪噪声信号，线性同余法的计算公式如下：

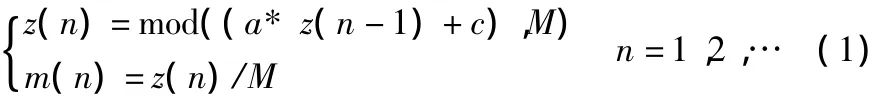
第一个式子是求(a*z(n－1)+c)与M相除的余数，第二个式子中的m(n)即为0－1之间的随机数，通过合理配置z(0)、M、a、c可以选择随机序列的频率分布。

1.2 最小二乘法模型辨识

本文模型辨识采用的算法为最小二乘法［10］。最小二乘法最初是通过解超定方程求最优解。设y为一组自变量X的函数：

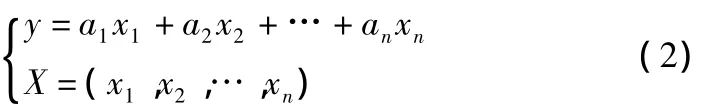
若对y进行m次观测实验，则有：

存在，即可求出待定参数：a=(a1，a2，…，an)－1。可证明存在唯一解：a=A－1Y。其中：

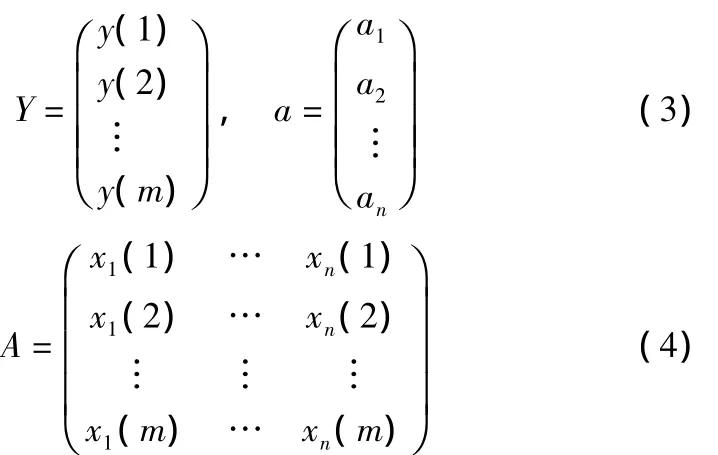
当m＞n时，方程数多于未知数个数，需要用估计方法估算最佳值。可以采用最小二乘法进行估计：

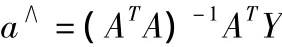
2 零相差跟踪控制算法

零相差跟踪控制的基本原理是基于模型的预测，利用已知未来信息设计系统的前馈补偿，理论上能够使被控对象系统的相位差在全频域内为0。其基本结构如图1。

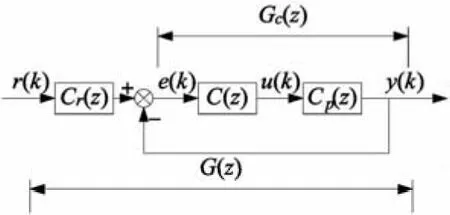
图1 零相差控制结构框图

图中r，e，u，y和Gp(z)分别表示系统输入，误差，控制器输出，系统输出以及离散时间控制对象。本文中C(z)是基于反馈的PI控制器，Cr(z)是以减小跟踪误差为目的而设计的零相差跟踪控制器。已知控制对象和反馈PI控制器组成的闭环系统的离散时间传递函数为：

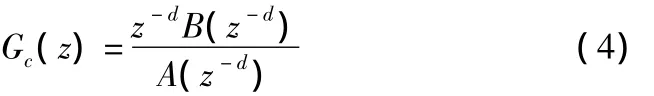
d表示系统延时，A和B为互质离散不等式。正常情况下机床系统不应该产生震荡，所以A不包含不稳定零点。

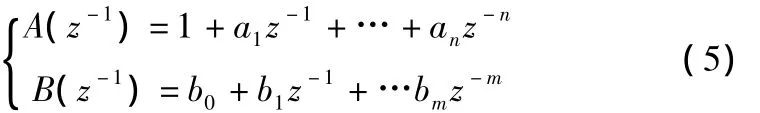
此处的A，B，d均由前文中所述辨识实验得出。

当Gc(z)为非最小相位系统时，B包含不稳定零点。按照zpetc原理，此时若取Gc(z)的逆为前馈控制器，B的不稳定零点将变成Gc(z)的不稳定极点，导致控制器的不稳定。一种证明有效的解决办法是将B分解为稳定部分Ba(z－1)和不稳定部分Bu(z－1)。

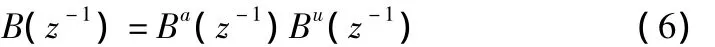
Ba(z－1)为单位圆内的系统零点组成的多项式，Bu(z－1)为单位圆外和单位圆上的系统零点组成的多项式。根据Tomizuka提出的设计方法，零相差跟踪控制器可表示为：

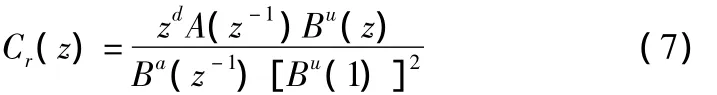
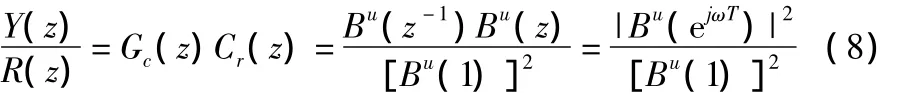
其中ω代表频域算子，可见传递函数无虚部，说明在所有频率处均无相位差。

此时经过前馈补偿矫正后的传递函数为：

3 实验设计及结果分析

3.1 试验台平台及试验流程

本实验是在RTX660三轴数控铣床上进行，实验机床如图2所示。

图2 RTX660三轴数控铣床试验台

该机床配有PA开放式数控系统，可通过该系统提供的接口对加工指令插补后的离散位置坐标和反馈位置进行实时读取计算和修改。该算法在每个插补器时钟周期内运行一次。插补时钟周期为2ms。电主轴采用德国GMN电主轴，最高转速30000r/min。电机和驱动器采用安川SGMSH-13ACA61，驱动器设为速度控制模式，控制参数通过其提供的离线整定方法自动确定，X轴和Y轴位置环增益在数控系统中分别设为2.95和3。实验流程如图3所示。

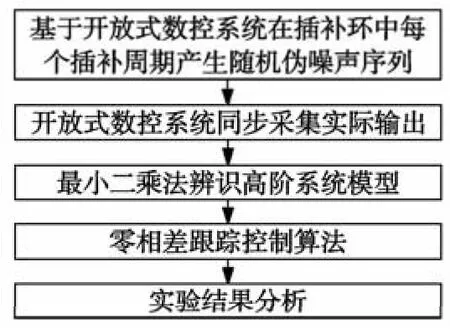
图3 实验流程

3.2 系统模型辨识实验

在公式(1)中取：z(0)=7、c=7、a=31、M=1021。此时随机伪噪声序列时域和频率分布如图4和图5所示。

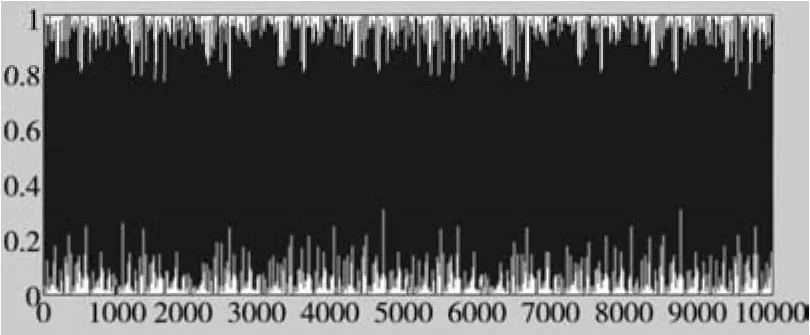
图4 随机伪噪声序列时域图

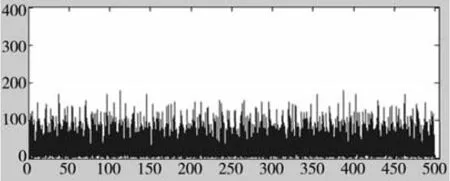
图5 随机伪噪声序列频域分布图

通过数控系统的二次开发功能，在数控系统插补器内设置计数器，每个插补周期计算一个伪随机信号作为数控机床X轴进给系统的速度指令输入，同时记录进给系统的反馈位置，系统的位置输入输出如图6所示。

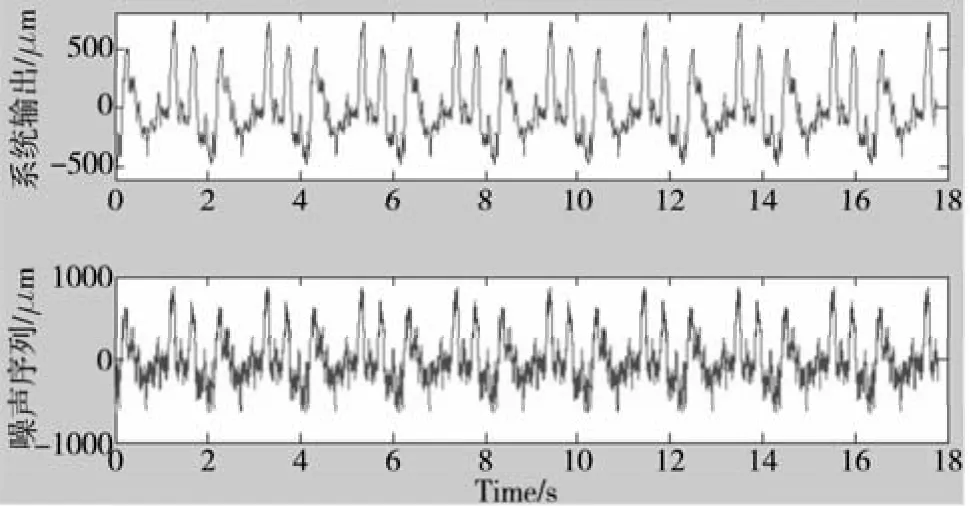
图6 系统辨识的输入输出

采用前述最小二乘法对激励信号数据和反馈位置数据估算进给估算，逐步加大模型阶数，直至残差变动很小为止。采用以上方法获取的X轴进给系统模型为：

3.3 基于开放式数控系统的零相位跟踪控制

根据辨识的系统模型可知，存在6个零点不能作为控制器极点，因此，根据公式(7)获取的零相差跟踪控制算法公式为：

设当前时刻为k，插补数据为r(k)此时通过零相差跟踪控制算法计算后输入到位置环的指令为：

公式(11)表明，为了使进给系统获取好的跟踪性能，零相差跟踪控制器需要预读9个插补数据。将算法嵌入开放式数控系统插补器中，每个插补器时钟周期实时更新插补数据和计算该周期输入到位置环的校正值并发送到运动控制器。

3.4 实验结果分析

3.4.1 单轴跟随特性比较

在开放式数控系统嵌入零相差跟随控制算法前后，对X轴进给系统输入正弦曲线指令，通过开放式数控系统实时读取其输出位置，通过计算工作台当前输出位置与当前指令位置的差，获得进给系统的跟随误差，数控系统插补器嵌入零相差控制算法前后其跟随误差如图7所示。

实验结果表明，嵌入零相差跟踪控制后，跟随误差基本消除，图中的几个尖峰是由于进给轴反向时由于摩擦力的低速非线性造成的。

3.4.2 两轴联动圆轨迹切削轮廓误差比较

为了比较零相差控制对联动加工轮廓误差的影响效果，进行了两轴联动加工圆轨迹实验，切削材料为铝合金，进刀量0.2mm，切削圆轨迹半径为40mm，切削速度为6m/min，主轴转速20000r/min。如图8所示。

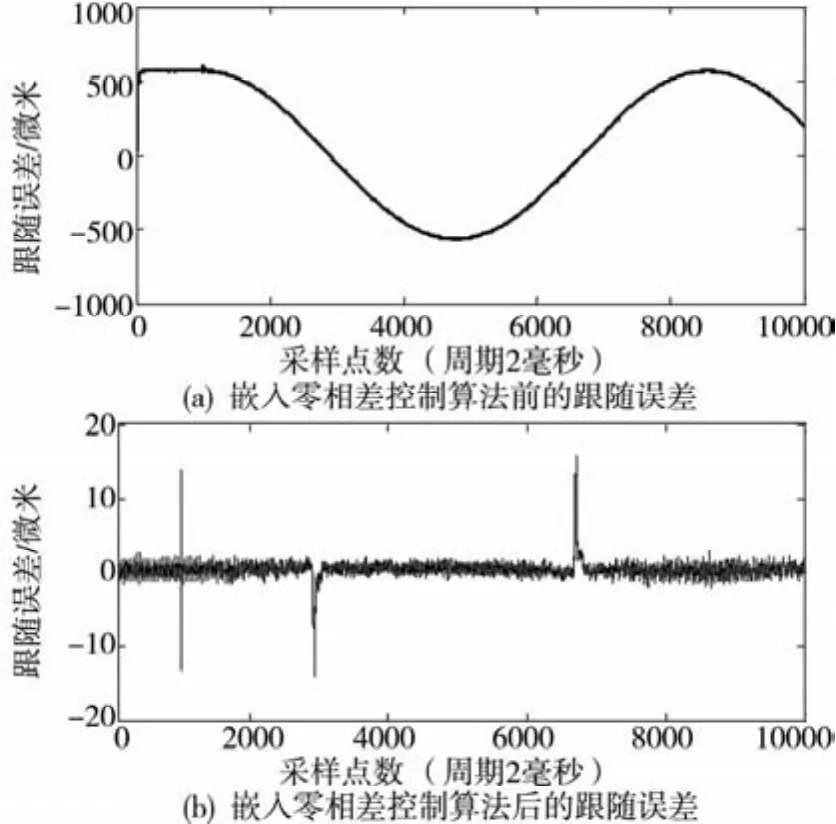
图7 嵌入零相差跟随控制前后跟随误差比较

图8 圆轨迹切削实验

通过开放式数控系统记录实际反馈位置后得到加工过程中的轮廓误差。采用相同方法设计Y轴零相差控制算法，将零相差控制算法嵌入插补器前后的轮廓误差比较如图9所示。

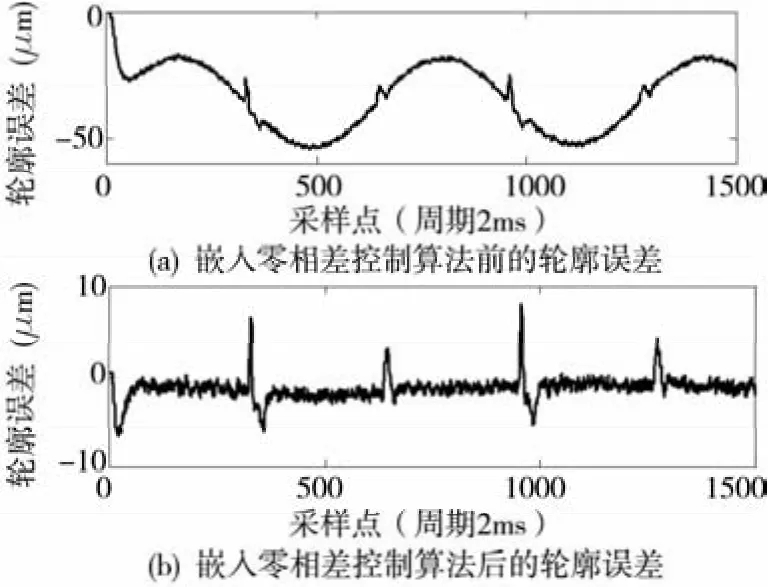
图9 嵌入零相差跟踪控制前后圆轨迹加工轮廓误差比较

实验结果表明，由于两轴机械传动系统参数和控制参数选取的不同，插补器嵌入零相差控制算法前，造成两轴联动圆轨迹存在超过50μm的轮廓误差，在插补器中嵌入零相差控制算法对两个轴分别进行前馈补偿后，其除了由于低速摩擦特性造成过象限误差外的轮廓误差得到很好地补偿。

4 结论

本文基于开放式数控系统的二次开发功能，对数控机床进给系统进行了模型辨识，设计了零相差跟踪控制器，并通过在插补器内预读插补位置数据和嵌入零相差跟踪控制算法，实现了进给系统的零相差前馈控制。通过单轴跟随特性和两轴联动加工的实验，验证了该方法能够有效的改善单轴进给系统的跟随性能以及多轴联动加工的轮廓精度。

［1］Ramesh R，Mannan MA，Poo AN.Tracking and contour error control in CNC servo systems［J］.International Journal of Machine Tools＆ Manufacture，2005，45(3)：301－326.

［2］Tomizuka M.Zero Phase Error Tracking Algorithm for Digital-Control［J］.Journal of Dynamic Systems Measurement and Control-Transactions of the Asme，1987，109(1)：65 －68.

［3］Funahashi Y，Yamada M.Zero Phase Error Tracking Controllers with Optimal Gain Characteristics［J］.Journal of Dynamic Systems Measurement and Control-Transactions of the Asme，1993，115(3)：311 －318.

［4］Tsao TC，Tomizuka M.Adaptive Zero Phase Error Tracking Algorithm for Digital-Control［J］.Journal of Dynamic Systems Measurement and Control-Transactions of the Asme，1987，109(4)：349 －354.

［5］Yeh SS，Hsu PL.An optimal and adaptive design of the feedforward motion controller［J］.Ieee-Asme Transactions on Mechatronics，1999，4(4)：428 －439.

［6］Wang X，Liu NF，Liu ZQ，et al.Zero Phase Error Tracking Control with Friction Compensation Based Motion Control System［J］.Icia：2009 International Conference on Information and Automation，Vols 1－3，2009：1174－1179.

［7］Liu XD，Wu YJ，Liu YM.Digital Servo Control Based on Adaptive Zero Phase Error Tracking Controller＆Zero Phase Prefilter［J］.2010 Chinese Control and Decision Conference，Vols 1－5，2010：3492－3497.

［8］Park HS，Chang PH，Lee DY.Concurrent design of continuous Zero Phase Error Tracking Controller and sinusoidal trajectory for improved tracking control［J］.Journal of Dynamic Systems Measurement and Control-Transactions of the Asme，2001，123(1)：127 －129.

［9］Koide D，Tokumaru H，Hishi K，et al.High-speed tracking servo using zero phase error tracking-feed-forward method for professional-use optical disks over 10000 rpm［J］.Japanese Journal of Applied Physics Part 1-Regular Papers Brief Communications＆ Review Papers，2007，46(6B)：3765 －3770.

［10］Adnan R，Samad AM，Tahir NM，et al.Trajectory Zero Phase Error Tracking Control Using Comparing Coefficients Method［J］.Cspa：2009 5th International Colloquium on SignalProcessing and ItsApplications， Proceedings，2009：385－390.

［11］Kim JS.A Feasible Approach for the Unified PID Position Controller Including Zero-Phase Error Tracking Performance for Direct Drive Rotation Motor［J］.Journal of Power Electronics，2009，9(1)：74 －84.

［12］Kraus F，Qiu XB，Schaufelberger W.Identification and control of a servo system［J］.(Sysid＇97)：System Identification，Vols 1－3，1998：197－202.