一种基于遗传模拟退火算法的航迹优化方法

杨晓龙，曲东才

(海军航空工程学院 a.研究生管理大队;b.控制工程系，山东 烟台 264001)

飞机地形跟踪飞行过程中由于飞行航路方向固定、飞越山顶时暴露时间过长，易被敌方发现和跟踪。地形回避(terrain avoidance，TA)是在保持飞机飞行高度不变的基础上，通过飞机横向机动来绕过地形障碍的一种超低空飞行技术［1］，它可以在保证飞行安全的前提下，进一步改善飞机的飞行隐蔽性，提高飞机执行低空突防任务的成功率。

本文主要对飞机地形回避的航迹规划进行研究，首先对地形障碍进行分类和建模，然后依据飞机地形回避的实际约束条件，利用改进狄克斯特拉算法进行初始航路规划，在保证飞行安全的基础上，运用遗传模拟退火算法对航路进行优化，寻找到整体航程最短的航路。

1 障碍空间建模

航迹规划是指在特定约束条件下，寻找运动体从初始点到目标点满足某种性能指标最优的运动轨迹，它是飞机进行地形回避飞行过程中的一个关键环节，是飞机成功实现低空突防的基础［4］。

地形障碍是飞机低空飞行的主要威胁来源，也是航迹规划中需要避开的主要障碍物。所以在飞机进行地形回避飞行过程中要首先对地形障碍进行建模分析，尽可能地保持模型的真实性和可靠性。

1.1 地形障碍建模

实际地形多种多样，要用一个统一的模型来表示各种地形往往比较困难。考虑海拔高度是地形的最直接的表述参数之一，而对于地形回避而言，由于飞行高度一定，海拔高度大于其飞行高度的地形均是威胁部分。

对地形进行采样后，选取出飞行障碍点集，并对其中各个采样点所属障碍的类别进行判定。因为同一个障碍的采样点间距紧凑，所以采用k均值聚类分析算法，对采样点集进行分类。k均值聚类算法是一种动态聚类法，该算法的基本思想为:随机选取k个初始聚类中心，按最小距离的原则将各个采样点分配到k类中的某一类，然后不断地循环计算类心、调整各采样点的类别，最终使得各采样点到其类心距离的平方和最小［5］。

通过k均值算法分类后，对同一类地形采样点进行统一考虑，建立地形模型。因为地形障碍边界的不确定性，为了同时满足对模型的精确性和统一表述的要求，只能采取折中的办法建立近似的模型，其方法为:用一个圆形模型来近似代替一个地形障碍，其中，每个类别的类心为圆心，取该类中所有样本点与类心距离的最大值为半径。这样圆心参数显示障碍的位置，而圆半径则反映出障碍的大小。图1所示的是在k均值聚类方法的基础上2个地形障碍的建模过程。

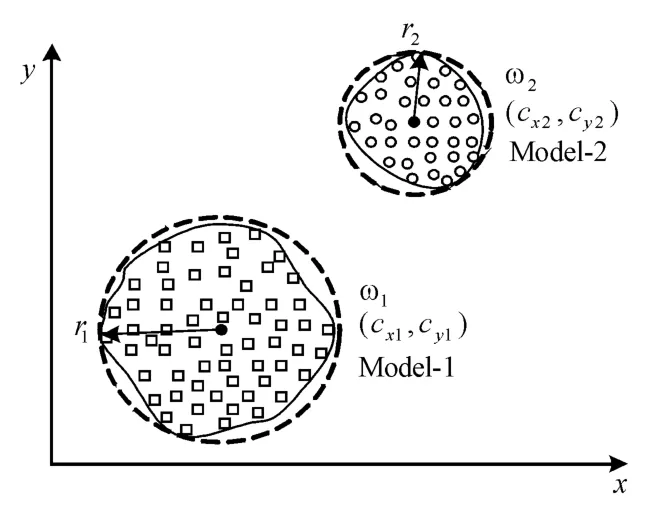
图1 地形障碍建模过程示意图

图1中，通过k均值聚类算法，将采样点分成2类，分别用圆形点和方形点表示，以类心(cx1，cy1)、(cx2，cy2)为圆心，采样点到类心距离的最大值r1、r2为半径，建立了地形障碍的近似模型。

1.2 建立可行节点空间

可行节点是指飞机可以安全飞行的节点，显然，在威胁空间里拥有无穷多个可行节点，为了降低算法的复杂度，缩短算法运行时间，需要减少可行节点的数量。本文进行初始航迹规划时选取障碍圆心之间的连线的中点和障碍圆心到地图边界连线的中点为可行节点。这样选取可行节点可以将飞机飞行过程中相对于临近的障碍威胁的危险系数降到最小。

检验每个可行节点的合法性，计算可行节点到每个障碍圆心的距离与其半径的差值Dij，判断该可行节点是否处于障碍模型内部，即

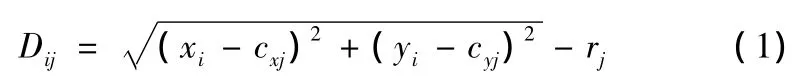
式中:i=1，2，…，n;j=1，2，…，k;Dij表示第 i个可行节点到第j个障碍圆心的距离与其半径的差值。

向量 Di=［Di1，Di2，…，Dij，…］，如果 Di中存在小于或等于0的元素，则可行节点i是不合法的，反之则为合法的可行节点。

建立可行节点空间后，2个可行节点之间的连线就构成了一段飞行航迹，给每段航迹赋权值，由可行节点为顶点，节点之间相互连接构成一个赋权图。Costij表示从可行节点i到可行节点j之间连线的代价函数。

并不是任何2个可行节点之间都有连线，这是因为2个可行节点的连线可能穿过某一障碍，此时该连线的代价函数的值为无穷大，如果飞机沿此航路飞行就会发生撞地的危险。

因此取代价函数的表达式

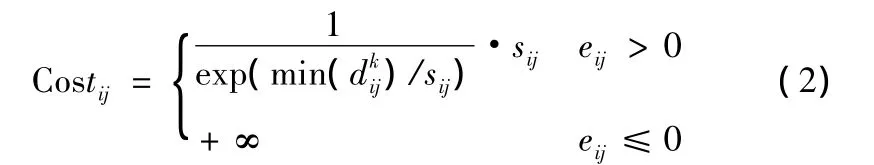
其中，sij表示可行节点i与j之间航路的长度;表示可行节点i与j之间航路到第k个障碍圆心的距离的，eij=min(-rk)，如果eij＞0则说明该航路合法，反之则不合法。由代价函数的表达式可以看出，代价函数与航路长度近似成正比，与航路的威胁系数近似成反比。

2 初始航迹规划

当障碍空间建模完成之后，就可以利用寻优算法搜索累计代价函数值最小的最优航迹。狄克斯特拉算法是一种典型的单源最短路径寻优算法，算法的基本思想是将赋权图中的顶点分为2组，第1组S存放已经确定最短路径的节点，第2组V存放未确定的节点。算法循环过程中按最短路径长度递增的顺序将V中的节点逐个移至S中，当终点被从V中移至 S 中时，算法循环结束［4，6］。

针对地形回避问题的特殊情况，对狄克斯特拉算法进行改进，加入航路最短距离smin和最大转弯角φ两个约束条件，保证规划出的航路能够满足飞机飞行条件。

改进狄克斯特拉算法流程:

1)初始化节点集S、V，将初始点p0放到S组，其余可行节点和终点pend放到V组，利用赋权图建立可行节点之间的邻接矩阵，初始化可行节点到初始点的最短路径d(v0i)(k=0)，(i=1，2，…，n)，k表示循环次数，如果初始点到可行节点有连接线段，则对应值为线段的权值，反之取极大值。

2)选择d(v0i)(k)中最小值d(v0j)(k)将节点j从点集V中移到点集S中。

3)根据节点j的邻接矩阵更新数据d(v0i)(k+1)。设ηj为以节点j为末端点的航路线段向量，ηji表示以j为起点，未确定节点i为结点的航路向量，则对于航路j→i的2个约束条件可表示为

满足式(3)则航路满足最小距离约束，满足式(4)，则航路满足最大转弯角约束，此时新的最短路径依照式(5)更新，否则不更新。

式(5)中，d(vji)是点集V中剩余节点到节点j的路径，如果剩余节点与j有连接线段，则对应值为线段的权值，反之取极大值。

4)重复第二和第三步，直到终点pend移到点集S中，此时d(v0n)(k)为初始点到终点的最短路径。

3 基于遗传模拟退火算法的航迹优化

初始航迹规划中的可行节点为连接线的中点，因此不是整个规划空间的最优航迹，利用遗传算法对规划初始航迹进行调整，让各航迹节点在相应的障碍端点连接线上滑动，得到新的航迹节点，根据新的航迹点进行规划，得到最优航迹。

遗传算法由于不受搜索空间限制性假设约束，不要求优化函数具备隐含并行性、连续、可导等假设，对于航迹规划这种含有大量模糊信息、多约束的优化问题来说，具有特别重要的意义。模拟退火算法模拟固体退火的温度参数T，在判断是否接受新解时依据Metropolis接受准则，既接受好的新解，同时按一定的概率对恶化解也接受，通过这样的判断，有效地避免了很多优化算法容易陷入局部极值和过早收敛的问题。

正是利用了模拟退火算法的优点，与遗传算法相结合，设计一种遗传模拟退火算法，在遗传算法的交叉和变异操作中引入Metropolis接受准则，避免了遗传算法陷入局部极值的问题。

3.1 基因编码方式

遗传算法首先需要确定基因编码方式，用以表达需要解决的问题。基因的编码方法除了决定个体基因染色体排列形式外，还决定了个体从搜索空间基因型变换到解空间表现型时的解码方法。

航迹规划中基因编码通常经纬度坐标系法，而单纯的经纬度坐标系法不能全面反映飞行器当前状态。因此，本文设计了一种动态链表染色体编码方案，它能减少航迹规划时重复计算量，提高了内存空间的利用效率，简化了插入和删除节点操作，其链表格式如图2所示。

图2 神经网络染色体结构

图2中Nn为航迹节点，Nni表示航迹节点的基因，其值如表1所示。这种基因编码方式虽然增加了计算机物理内存，但是减少了重复计算量，同时，便于实时提取飞行器航迹相关信息，在不用解码的情况下，就可以直接计算参考航迹的代价函数值，更接近问题的原始形式，表达式更有效，更能够生成好的解。

表1 基因编码在航迹中的物理意义

3.2 适应度函数

在遗传算法航迹规划中，适应度是评价航迹优劣的唯一标准。个体适应度评价函数，直接影响遗传算法的计算效率和计算时间。它通过威胁源、航迹距离、安全高度和约束违背量等评价因素指标，评定满足初始点到目标点的可行航迹。从本质上讲，航迹规划的目标就是使航迹的适应度更优。

对于地形回避系统，可行航迹的飞行高度一致，对威胁都已进行有效回避，只需考虑航迹总航程即可，因此可以取适应度函数f(n)为航迹总航程。

3.3 遗传操作算子

遗传操作算子是遗传算法具备强大搜索能力的核心，是调整和控制进化过程的基本工具。在航迹规划中，由于算法特殊的基因编码方式，遗传操作算子需要进行改进以满足其实现航迹规划任务。为此对遗传算子进行的特殊处理，将其应用于航迹节点，从而生成更好的航迹路径。

1)选择算子。选择运算使用比例选择算子，是利用比例于各个个体适应度的概率来确定子孙被选择的可能性，设种群数量为M，个体i的适应度为fi，则个体i被选中的概率为

个体的概率给定以后，随机产生［0，1］之间的随机数，如果个体的选择概率大于此数则被选中，小于此数则被淘汰，从而那些高适配值个体被选中的概率就大，低适配值个体就容易被淘汰。

2)交叉算子。将2条航迹重新组合，生成新的航迹。交叉运算采用单点交叉算子，只有一个交叉点。生成2个新的子代个体可以可行，也可以不可行，且航迹节点数可以不相同。交叉概率pc一般选为0.25～1。

3)扰动算子。对航迹节点中的一个节点坐标随机进行改变，使其沿着相应障碍的端点连线进行滑动，得到新的航迹。

3.4 算法描述

遗传模拟退火算法航迹规划的基本步骤如下:

1)设定种群的规模M，最大遗传操作代数为N，初始温度T=T0，温度更新次数l=0，设定温度变化按照 Tl+i=0.9Tl，设定终止温度 Te;

2)生成初始种群Pl(k)，k=0;

3)计算种群Pl(k)中的每个染色体的适应度函数，按照适应度的大小根据比例算子选出M个染色体组成新种群Pls(k+1);

4)将新种群Pls(k+1)中染色体按照传统方法进行交叉操作得新种群Plcl(k+1)，设种群Pls(k+1)中个体i和个体j进行了交叉得到种群Plcl(k+1)中个体i'和个体j'，交叉前2个个体i和j的适应值分别为f(i)和f(j)，交叉操作后2个个体i'和个体 j'的适应值分别为 f(i')和 f(j')，按照下式Metropolis接受准则经过若干次的迭代得到新种群Plc(k+1)

5)变异操作与交叉操作类似，将Plc(k+1)变异得到Plm1(k+1)，然后对变异后的各个个体依据式(9)得到新的种群Plm(k+1)

式(9)中i和i'分别表示变异前和变异后的个体，适应值为f(i)和 f(i')。

6)将Plm(k+1)赋给Pl(k)，同时k=k+1。判断k是否小于N，如果是则转至第7步，否则转至第4步。

7)更新温度 Tl+i=0.9Tl，l=l+1，并且更新种群Pl+1(k)=Pl(k)。如果满足停止准则，则停止计算输出最优解;否则转至第4步。

4 实例仿真

对本文提出的航迹优化方案进行验证，构建一个3000 m2区域的数字地图［7］，在高度为300 m的基准平面内进行地形回避航路规划。

首先构建基准平面图，如图3所示。在此基础上，对平面图中的4个地形障碍运用k均值算法聚类建模，建立障碍空间模型。如图4所示。

设置飞行起点为p0=(200，2800)、飞行终点为pend=(2800，200)，进行初始航迹规划，得到初始航路图。在初始航迹的基础上，运用遗传模拟退火算法对航迹进行优化，设种群大小为50，以航迹的总航程为适应度值对航路进行优化，循环迭代100次后，得到航迹曲线如图5中，图5中实线所示初始航迹，虚线表示优化航迹，图6将规划的航迹还原到数字地图中，遗传模拟退火算法的适应度值变化曲线如图7所示。

图3 基准平面

图4 k均值算法聚类建模

图5 优化航迹曲线

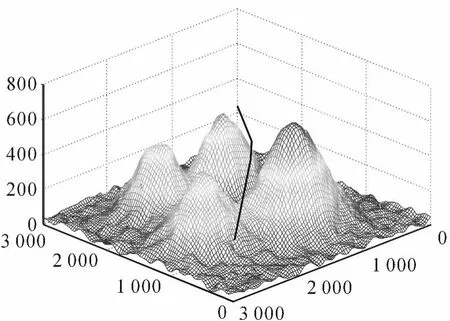
图6 优化航迹3D示意图

图7 适应度值变化曲线

5 结束语

本文对飞机地形回避飞行进行航路规划研究，通过k均值算法实现了对地形障碍采用点的聚类，并在此基础上完成了对地形障碍空间的统一建模，通过狄克斯特拉算法完成了对飞行航迹的初始规划，然后在此基础上运用将模拟退火算法用于遗传算法实现了对航迹的优化，仿真结果显示经过优化后的航迹在保证航路安全的基础上，缩短了整个航路的航程，达到了优化的目的，证明了本文提出的方案的可行性和合理性。

［1］闵昌万，袁建平.军用飞行器航迹规划综述［J］.飞行力学，1998，19(2)：13-18.

［2］沈春林，徐克虎，贺也平.低空突防中的若干关键技术［J］.南京航空航天大学学报，2003(3)：134-139.

［3］范洪达，马向玲，叶文.飞机低空突防航路规划技术［M］.北京：国防工业出版社，2007：7-8，105-107.

［4］黄明.武装直升机航迹规划与轨迹控制研究［D］.南京：南京航空航天大学，2004：12-16.

［5］孙即祥.现代模式识别［M］.长沙：国防科技大学出版社，2002：30-32.

［6］项林斌，秦硕，黄学宇，等.一种无源自动地形跟随系统的设计［J］.弹箭与制导学报，2005，25(2)：635-639.

［7］StephanWei，Markus Achtelik，Laurent Kneip.Intuitive 3D Maps for MAV Terrain Explorationand Obstacle Avoidance［J］.J Intell Robot Syst，2011(61)：473 – 493.

［8］王美仙，李明，张子军.飞行器控制律设计方法发展综述［J］.飞行力学，2007，25(2)：1-5.

［9］Sterens B L，Lewis F L.Aircraft Control and Simulation［M］.New York：John Wiley and Sons INC.，1992：175-240.

［10］辛贵州.无人飞行器航迹规划算法研究［D］.哈尔滨：哈尔滨工程大学，2010：48-50.