小波包与混沌和神经网络相结合的人民币汇率预测研究

■殷光伟 沈阳工业大学经济学院 沈阳工业大学金融市场和风险管理研究所

■高丽峰 付岱山 万志华 沈阳工业大学经济学院

自2005年7月21日起，我国开始实行了以市场供求为基础、参考一篮子货币来进行调节、有管理的浮动汇率制度。至此，人民币汇率不再盯住单一美元，人民币汇率的变动趋势变得更加复杂化，对人民币汇率的准确预测也变得更加困难。

人工神经网络是一种非参数的数据驱动型的方法，由于其具有能够逼近非线性的能力，在预测领域中得到了比较广泛的应用；但是，当将人工神经网络用于人民币汇率预测时，并不能得到理想的效果。汇率系统具有混沌特性，由于混沌具有一定的确定性，使得它具有有限预测能力，因此，对汇率系统长期演化行为进行预测是不可行的，而对其短期行为进行预测是可行的。然而，当采用混沌模型对汇率系统进行短期预测时，效果也不能令人满意。究其原因还是汇率时序太复杂。由于汇率时序太复杂，因此很难对其准确预测。

为了更好地对人民币汇率进行预测，本文提出一种组合预测方法，将小波包变换引入到人民币汇率预测中，并将其与混沌和神经网络相结合进行预测，以期提高人民币汇率预报的精度。

一、相关理论

1.小波包简介。设{Vj；j∈Z}（Z是整数集）构成L2（R）（R是实数）上的正交多分辨分析，其尺度函数和母波函数分别为φ（t）和（t），它们满足以下二尺度方程

其中，系数hk与gk系数满足下面条件

对于固定尺度情况，定义一系列递归函数如下

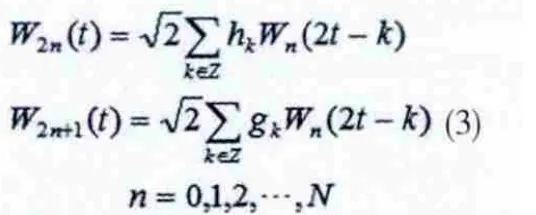
则由(3)式所确定的函数序列Wn(t)（n=0,1,2,…,N）称为由W0=φ确定的小波包。

2.混沌理论简介。混沌理论主要是研究自然界非线性过程内在随机性所具有的特殊规律性，揭示非线性系统中有序和无序、确定性与随机性的统一。

重构相空间是混沌理论的一个重要内容之一，其目的是在高维相空间中恢复决定时序动力系统的混沌吸引子。

在重构相空间中，嵌入维数m的选取非常关键。通常有两种方法可用来计算嵌入维数，即关联维数法和虚假邻域法，但它们有共同的缺陷，就是在选择嵌入维时都包含主观参数或主观判断。而学者Cao L.提出一种基于零阶近似的方法来计算嵌入维数，也称为零阶近似法，这种方法在选择嵌入维数时不依赖主观参数，故文中采用此方法来计算嵌入维数。

3.人工神经网络简介。人工神经网络，简称神经网络，是模拟生物神经网络进行信息处理的一种数学模型。神经网络由大量的人工神经元相互连接来进行计算，并能够根据外界的信息来改变自身的结构；它主要是通过调整神经元之间的权值对数据进行建模，并最终达到具备解决实际问题的能力。

神经网络结构一般有三个层次，即输入层、隐含层和输出层，各层次顺次连接。其中，输入层连接外部输入模式，并由各输入单元传送给相连的隐含层各单元；隐含层是神经网络的内部处理单元，神经网络所具有的模式变换的能力主要体现在隐含层单元的处理功能上；输出层则产生神经网络的输出模式。

神经网包括很多种，其中最常用的一种是BP神经网络。BP神经网络是一种以误差反向传播为基础的前向网络，具有非常强的非线性映射能力。在实际应用中，大约80%神经网络模型采用了BP神经网络或BP神经网络的变化形式。本文采用的神经网络也是BP神经网络。

二、实证分析

1.实证研究设计。人民币兑美元汇率数据具有多尺度特性，针对这一多尺度特性，本研究提出一种小波包变换与混沌和神经网络结合的汇率时间序列预测模型。实证步骤如下：

（1）通过小波包变换，将原始时间序列分解成不同尺度水平的子序列；（2）利用混沌理论对变换后所得到的从低频到高频的不同频率的子序列分别进行分析，以确定各子序列都具有混沌特性；（3）基于混沌信息和神经网络对各子时间序列构建模型，简称为混沌-神经网络模型，并对所构建模型进行训练和预测；（4）最后将由基于混沌信息和神经网络构建模型进行预测所得到的子时间序列预测结果进行小波包重构，得到汇率时间序列的预测结果。

2.实证过程与结果分析。本文选取2010年12月1日至2010年12月30日共22个交易日的每100美元/人民币每日分时汇率数据为实证研究的原始数据。数据来源于http：//fx.Sauder.Ubc.ca/data.html。每个交易日的汇率数据是取自从8:00到17:00的10个整点的汇率卖出价。

(1)小波包分解与特性分析。按照实证步骤，首先要对人民币汇率序列进行小波包分解，根据预测误差最小的原则，确定分解的层数为三层，这样就将原始时间序列分解成从低频到高频八个频率成分的子序列。

对汇率进行小波包分解之后，还需要对分解所得的各子序列进行混沌特征分析与判别，以确定它们是否具有混沌特征。进行混沌分析与判别的标准，是要看各子序列的最大Lyapunov指数是否为正，如果为正，则可判断是混沌的。本文采用小数据量方法求取各子序列的最大Lyapunov指数，其计算结果都为正值，因此，可以判断各子序列都具有混沌特征，都是混沌时间序列。

(2)混沌-神经网络模型构建。由于各子序列都是混沌时间序列，在各子序列中必然隐含有混沌的信息，因此，可基于混沌信息和神经网络来构建各子序列的预测模型，即混沌-神经网络模型。

混沌-神经网络实际上是“特殊”的神经网络，之所以“特殊”，是因为它是利用混沌时间序列的混沌信息来确定神经网络输入层的神经元数目。而一般的神经网络在确定输入层神经元的数目时，都没有考虑混沌信息。因此，混沌-神经网络与一般神经网络的区别是在于输入层神经元数目的确定方式有所不同。

利用混沌信息来确定神经网络输入层的神经元数目，是指把混沌时间序列重构相空间的最佳嵌入维数作为输入层的神经元的数目。这样，只要重构相空间的最佳嵌入维数能够计算出来，那么输入层的神经元数目也就确定下来。

本文采用零阶近似法来计算各子序列重构相空间的最佳嵌入维数，结果如表1所示。

表1中的计算结果即可作为从低频到高频的各子序列预测模型的输入层神经元数目。

表1 重构相空间的最佳嵌入维数

输入层神经元数目确定后，还需要确定网络层数、隐含层神经元数目以及输出层神经元数目等参数，这些参数的确定方式与一般神经网络相关参数的确定方式相同。具体结果如下：

①确定网络层数。由于一个具有单隐含层的神经网络只要包括足够多的神经元个数就可以逼近任意连续函数，因此，本文针对从低频到高频各个子序列所构建的预测模型都只有一个隐含层。

②确定隐含层神经元数目。对隐含层神经元数目的确定可采取试凑法或经验公式来进行。具体结果如表2所示。

表2 隐含层神经元数目

③确定输出层神经元数目。输出层神经元的数目是根据实际问题来确定的。本文所做的汇率预测为一步向前预测，因此，对每个子序列所做的预测也为一步向前预测，每个子序列的预测模型的输出数据都只有1个，所以每个模型的输出层神经元的数目都只有1个。

输入层神经元数目、网络层数、隐含层神经元数目、输出层神经元数目等参数确定后，还需要确定每个模型的传递函数、训练方法及初始权值等，这些也是构建模型的主要工作。

(3)预测结果与分析。模型构建完成后，可采用trainlm函数和Levenberg-Marquardt算法对网络进行训练和学习。之后，就可应用所构建的模型（即模型1、模型2、模型3、模型4、模型5、模型6、模型7、模型8）分别对子序列（即序列1、序列2、序列3、序列4、序列5、序列6、序列7、序列8）进行预测。

本文进行实证研究的汇率数据，样本数量共有220个，因此，经三层小波包分解后所得到的每个子序列也均有220个数据。对每个子序列进行预测时，是以每个子序列的前200个数据作为网络的训练样本，而后面20个数据则作为测试样本用以检验网络预测效果。

每个子序列的的预测结果得到之后，再将它们应用小波包理论进行重构，即可得到最终的预测结果，预测结果如图1所示。预测的均方根误差为0.0153，平均绝对误差率为0.0015574%，预测方向精度为0.9474。可见预测效果很好。

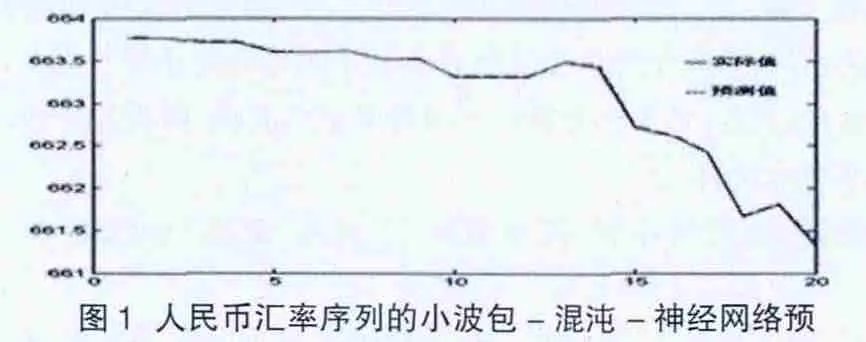
本文也采用小波包与神经网络结合的方法对汇率进行了预测。预测的均方根误差为0.0253，平均绝对误差率为0.0030932%，预测方向精度为0.8947。

由预测指标对比分析可知，基于小波包与混沌和神经网络相结合方法的预测效果明显优于基于小波包与神经网络相结合方法的预测效果。

为进一步确认本文所提方法的有效性，本文还以2005-07-21至2010-12-30美元兑人民币日汇率数据为实证数据进行研究。实证数据共1372个，以前1367个数据为样本对后5个数据进行预测，预测均方根误差为0.0023，平均绝对误差率为0.027299%，预测效果仍然很好。而采用小波包与神经网络结合的方法对日汇率进行预测，其预测均方根误差为0.0032，平均绝对误差率为0.036871%，因此仍可以得出结论，本文所提方法的预测效果明显优于基于小波包与神经网络相结合方法的预测效果。由此可以得出，本文所提方法对人民币每日分时汇率和日汇率的预测都具有有效性。

三、结论

本文提出了一种人民币汇率建模及其预测的小波包与混沌和神经网络相结合的三阶段汇率时间序列预测方法。通过对比小波包与混沌和神经网络相结合的预测与小波包与神经网络相结合的预测，本研究发现，虽然小波包与神经网络相结合的预测效果已经很好，但小波包与混沌和神经网络相结合的预测效果则更好，预测精度更高。这说明本文提出的方法能更好地刻画时间序列的规律，更好地把握汇率价格变化的特征。采用此方法对人民币汇率进行预测，其预测结果会更加准确。

[1]刘贵忠,邸双亮.小波分析及其应用[M].西安电子科技大学出版社,1992.

[2]秦前清,杨宗凯.实用小波分析[M].西安电子科技大学出版社,1994.

[3]Grassberger P, Procaccia I.Characterization of stranger attractors [J],Physical Review Letters,1993, 50(5): 346～349.

[4]Matthew B Kennel, et al, Determining embedding dimension for phase-space reconstruction using a geometrical construction[J], Physical ReviewA,19923, 45(6): 3403～3411.

[5]Cao L.Practical method for determining the minimum embedding dimension of a scalar time series [J].PhysicaD, 1997, 121: 75—88.

[6]Rosenstein, M.T., Collins, J.J., De Luca, C.J.A practical method for calculating largest Lyapunov exponents from small data sets [J].Physica D,1993, 65: 117—134.