一类非线性脉冲时滞差分方程的振动性

田海燕

（山西大同大学数学与计算机科学学院，山西大同037009）

一类非线性脉冲时滞差分方程的振动性

田海燕

（山西大同大学数学与计算机科学学院，山西大同037009）

研究了一类非线性脉冲时滞差分方程解的振动性，得到了该方程所有解振动的一个充分条件。

非线性；脉冲时滞差分方程；振动性

近年来，对于时滞差分方程的研究已经有了大量的成果[1]。同时脉冲微分方程振动性研究也有不少的研究成果发表，但脉冲差分方程尤其是非线性脉冲时滞差分方程的振动性成果还比较少。文献[2]研究了具有多时滞的线性脉冲差分方程

得到了方程所有解振动的若干充分条件。

考虑如下形式更一般的非线性脉冲时滞差分方程

1 预备知识

引理1 设0≤bk＜M，nk+1-nk＞K，k=1，2，3，…，且有pi（n）≥0，如果则方程（1）的所有解振动。

引理2 若｛xn｝最终为正，且存在自然数v，使对所有k≥v，有限数列｛xnk+1，xnk+2，…，xnk+1｝单调不增。如

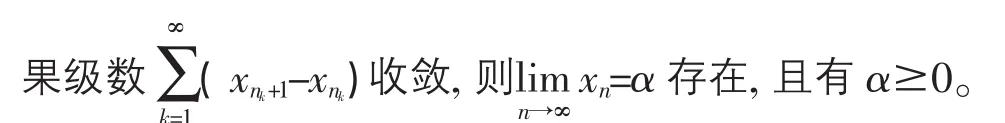
2 主要结论

则方程（4）的所有解振动。

证明 反证法。设方程（4）有一解是非振动的，不失一般性，设方程（4）有一个最终正解｛xn｝，则由条件知最终有fi（n，xn-ki）＞0，从而由方程（4）知最终有

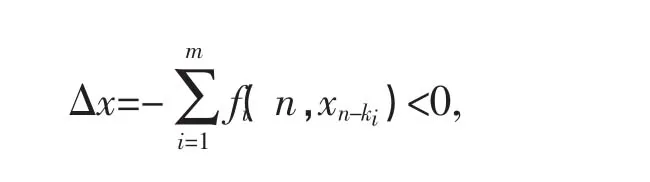
于是由引理1可知方程 （1）的所有解振动，这就与｛xn｝是（1）的一个最终正解矛盾。故方程（4）的所有解振动。定理证毕。

[1]张广，高英.差分方程的振动理论[M].北京：高等教育出版社，2001.

[2]魏耿平，高平.具多滞量脉冲差分方程的振动性[J].湖南大学学报，1999（S1）：4-6.

[3]申淑媛，翁佩萱.具有脉冲的非线性时滞差分方程的振动性和渐近性[J].华南师范大学学报，2005（2）：93-98.

[4]葛礼霞，姬春秋，赵文英.一类非线性脉冲时滞差分方程的振动性和渐近性[J].山东理工大学学报，2009（5）：90-92.

〔责任编辑 高海〕

Oscillation of Nonlinear Impulsive Delay Difference Equations

TIAN Hai-yan
（School of Mathematics and Computer Science，ShanxiDatong University，Datong Shanxi，037009）

In this paper，we study oscillation of the nonlinear impulsive delay difference equation.The sufficient conditions are obtained for oscillation of all solutions of the equation.

nonlinear；impulsive delay difference equation；oscillation

O175

A

1674-0874（2013）06-0005-02

2012-08-08

国家青年科学基金项目[11301312]

田海燕（1984-），女，山西朔州人，硕士，助教，研究方向：微分方程。