交通流的混沌特性分析及其预测＊

罗 轶

（湖南师范大学物理与信息科学学院，湖南长沙 410081）

交通流的混沌特性分析及其预测＊

罗 轶

（湖南师范大学物理与信息科学学院，湖南长沙 410081）

实时准确的短时交通流预测是智能交通系统中实现交通控制和诱导的关键技术之一.首先，采用饱和关联维数法和互信息量法对交通流时间序列的嵌入维数和延迟时间进行计算，并根据计算结果对交通流时间序列进行相空间重构；然后，采用wolf方法计算其最大Lyapunov指数，并对其进行功率谱分析，结果表明，交通流时间序列具有噪声；最后，分别采用基于BP神经网络和RBF神经网络的预测模型对交通流时间序列进行预测，结果表明，2种模型对短时交通流均能较好预测，但后者的预测精度较高，预测速度较快.

嵌入维数；延迟时间；相空间重构；BP神经网络；RBF神经网络

随着中国社会经济的快速发展，交通拥堵问题在大中城市普遍存在，交通拥堵不仅极大地影响城市居民出行，而且产生的汽车尾气和噪声污染严重影响城市环境.目前智能交通系统成为了解决交通拥堵问题的一种新思想和新技术.交通诱导和控制是实现智能交通的核心技术之一，实时准确的交通流预测则是实现交通诱导和控制的前提.道路实时观测数据所构成的时间序列是进行交通流预测的基础.由于交通流数据具有短期性和实时性，所以其通常表现出不规则的复杂动力学行为，快速识别短时交通流中的混沌是应用混沌理论进行交通流预测的前提.目前，国内外已有不少学者应用神经网络进行短时交通流预测，并取得了一定成果.考虑到交通流量具有动态性的特点，笔者采用基于BP神经网络和RBF神经网络的预测模型对短时交通流进行预测，研究了人工神经网络在交通流预测中的应用.

1 交通流混沌特性分析

1.1 交通流时间序列的相空间重构

道路实时采集的交通流时间序列是1维的标量时间序列，其低维的相空间根本无法完全反映出交通流复杂的动力学特性，所以对交通流时间序列进行混沌特性分析的首要任务是完成相空间重构，经过重构后，标量时间序列被映射成多维序列，且该多维序列相空间与原标量时间序列的相空间等价，从而能够全面描述交通流复杂的动力学特征.依据Takens定理［1］，对交通流时间序列q（n），采样点n＝1，2，...，N，采用基于延迟坐标的相空间重构法进行重构可得

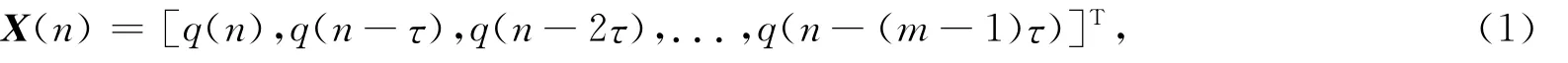
其中：X（n）为相空间重构后的多维交通流时间序列；n＝（m－1）τ＋1，...，N；τ为延迟时间；m为嵌入维数.由（1）式可知，选择合适的嵌入维数m和延迟时间τ将是实现交通流相空间重构的关键.

延迟时间τ是时间序列的动力学特性中最重要的参量之一.若选择的τ过小，时间序列的相空间轨迹将受到挤压，导致相空间矢量中的任意2个分量因为在数值上非常接近而无法相互区分；若τ选择过大，将引发后续时刻动力学形态的剧变，使得混沌吸引子的轨迹在2个方向上的投影毫无相关性可言［2－4］.文献［3］介绍了多种求解延迟时间的方法，包括自相关法、互信息量法和C-C方法.笔者采用互信息量法来计算交通流时间序列的延迟时间，其步骤如下：

（1）选定离散时间序列X＝｛x1，x2，...，xm｝，并产生延迟时间为τ的离散时间序列Y＝｛y1，y2，...，yn｝，其中m＝n，xi＝yi＋τ.

（2）计算序列X和Y关于τ的互信息量函数：

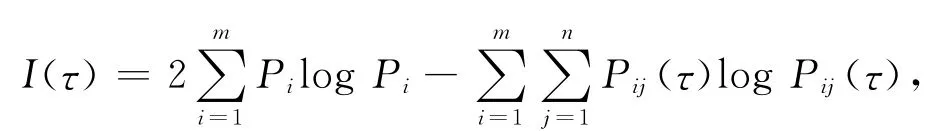
其中P（x）为事件x发生的概率.

（3）作出时间延迟与互信息量之间的关系图，图中平均互信息量为第1个局部最小值时所对应的时间延迟即为选定的最佳时间延迟.

计算嵌入维数m的目的是使短时交通流序列相空间重构前的吸引子和重构后的吸引子等价.若m选取过小，混沌吸引子可能会发生折叠以至在某些地方出现自相交，重构得到的多维空间不能完全涵盖原序列的特征；若m选择过大，则会大幅增加计算量，而且噪声和舍入误差的影响也会进一步放大［2－4］.文献［3］介绍了多种求解嵌入维数的方法，包括试算法、虚假最近邻点法和饱和关联维数法等.笔者采用饱和关联维数法即G-P算法来计算交通流时间序列的嵌入维数，其步骤如下：

（1）先给定一个较小嵌入维数m＝m0，产生一个重构的相空间，如（1）式所示.选取｛X（1），X（2），...，X（n）｝相空间内任意不相交的两点X（i）和X（j）.

（2）计算关联函数

其中：‖X（i）－X（j）‖为相点X（i）和X（j）之间的欧氏距离；H（·）是Heaviside函数（阶跃函数）；r为临界阈值.

（3）调整阈值r的取值范围，计算ln C（r）.

（4）增加嵌入维数m＝m1＞m0，重复步骤（2）和（3），画出嵌入维数m取不同值时ln C（r）与ln r的关系图.

1.2 交通流的功率谱分析

在实际应用中，受到检测和提取方法以及计算工具的限制，使得交通流序列不可避免的存在噪声，若仅在时域内对交通流序列进行观测，则难以有效地分辨其真实特征.笔者采用功率谱分析的方式对交通流时间序列的混沌特性进行定性分析，其步骤如下：

（1）选定交通流时间序列q（1），q（2），...，q（N），设定周期条件q（n＋N）＝q（n），计算序列的自相关函数为

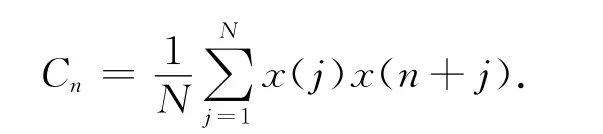
（2）对Cn进行离散傅里叶变换，其傅氏系数为

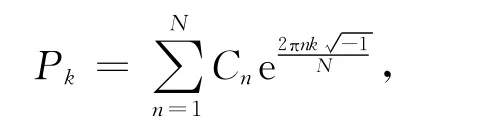
周期序列、混沌序列和随机序列均能通过功率谱得到很好地区分.周期或拟周期序列的功率谱具有单峰或几个峰，混沌序列的功率谱图无明显的峰值或峰连成一片形成宽峰，随机序列的功率谱与频率无关，连续且无明显峰值［2］.

1.3 最大Lyapunov指数的计算

笔者采用计算最大Lyapunov指数的方式对交通流序列的混沌特性进行定量分析.Lyapunov指数λ表征了时间序列在相空间中相邻运动轨道间收敛或发散的平均指数率，它的大小直接决定了该时间序列是否具有混沌特性，其中最大Lyapunov指数是动力学特性中最为重要的参量.格里波基证明只要最大Lyapunov指数大于零，就可以肯定混沌的存在［2］.当最大Lyapunov指数大于零，即混沌存在的前提下，最大Lyapunov指数越小，则运动轨道短期内发散率相对较小，此时该混沌序列具备的可预测性较好.文献［2］介绍了多种求解最大Lyapunov指数的方法，包括Wolf方法、Jocobian方法和小数据量方法等.笔者采用wolf方法来求解最大Lyapunov指数，其步骤如下：

（1）根据选定的延迟时间τ和嵌入维数m对交通流时间序列进行相空间重构得到X（n），如（1）式所示.

（2）取初始时间点n0、任意时间点ni和最终时间点nM.首先计算X（n0）与其最近邻点X0（n0）的最近距离L0＝‖X（n0）－X0（n0）‖，随着时间演化到时间点ni，L′0＝‖X（ni）－X0（ni）‖大于某一规定值ε（ε＞0），保留X（ni），并找到其最近邻点Xi（ni），使得Li＝‖X（ni）－Xi（ni）‖＜ε，重复上述过程直到时间终点nM.

（3）计算最大Lyapunov指数

2 基于神经网络的交通流预测

2.1 BP神经网络

BP神经网络又称为误差反向传播（Back Propagation）神经网络，它是一种由信息正向传播和误差反向传播2个过程组成的多层前向型神经网络.BP神经网络通常由输入层、中间层（隐含层）、输出层等3个部分组成.各层之间实现全连接，而各层内神经元之间无连接.BP神经网络采用有监督学习方式进行学习，训练过程需要提供输入向量和期望输出响应.将期望输出响应与实际输出响应之间的误差从输出层反向经过中间层传输到输入层并逐层修正各自连接权值的过程称为反向传播.由于误差反向传输，BP神经网络采用的传递函数必须是可微的，通常采用sigmoid型函数、正切函数tansig和线性函数purelin.［4－6］

2.2 RBF神经网络

径向基函数（Radial Basic Function，RBF）神经网络是一种由输入层、隐含层和输出层这3层组成的前向型网络.一些源点（感知单元）组成了输入层，实现网络与外界的连接.隐含层通常采用高斯函数、多二次函数、逆多二次函数等径向基函数，实现输入层到隐含层之间的非线性变换，该层神经元数目依据描述问题的复杂程度来确定，通常数量较大.输出层采用线性函数对输入层的信号进行响应.RBF神经网络的核心思想是：隐含层采用径向基函数作为隐单元的“基”构成隐含层空间，将输入向量不通过权值连接的方式直接映射到隐空间，该映射关系随径向基函数中心点的确定而确定.由于隐含层空间与输出空间之间采用线性函数进行映射，所以将采用网络可调参数作为权值的隐单元输出线性加权和作为网络的输出.由于该权值可由线性方程直接解出，所以RBF神经网络的学习速度较快并能避免BP神经网络中常见的局部最小问题.［7－8］

2.3 基于神经网络的交通流预测模型构建与评估

基于神经网络的交通流预测模型构建流程如下：（1）交通流数据的采样与整理.确定预测方式、输入序列矩阵、输出序列矩阵、输入目标序列矩阵和输出目标序列矩阵.（2）分别使用互信息量法和G-P算法计算延迟时间τ和嵌入维数m，并对交通流序列进行相空间重构.（3）对交通流序列进行功率谱分析，同时采用wolf方法对相空间重构后的交通流进行最大Lyapunov指数计算，从而对交通流序列的混沌特性作定性和定量分析.（4）采用BP神经网络和RBF神经网络对交通流序列进行预测.（5）将实际预测值与期望预测值进行对比，根据预测效果调整模型参数.

笔者采用平均绝对偏差εmad、均方根误差εrmse、平均绝对百分比误差εmape和标准均方根误差εnrmse等4个误差指标对2个模型的预测结果进行评估.各误差指标的计算公式如下［4］：

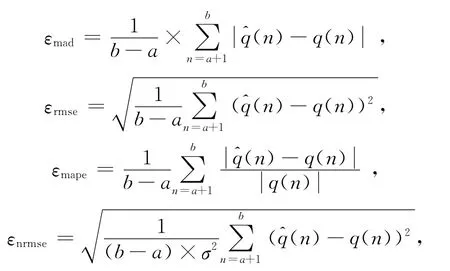
3 实验与分析

文中所采用的交通流数据为2010年1月18日至2010年1月22日（周一至周五）间，北京市西直门桥处方向为至西向东断面的混合交通流流量数据.数据的采样间隔为10min，共720个采样点数据.所有仿真结果均在Intel双核T5470，1.6GHz，内存2GB的MATLAB R2009a仿真环境下完成.

3.1 延迟时间和嵌入维数计算

利用互信息量法得到的交通流时间序列的互信息量函数图如图1所示.从图1中可以看出：当C＝1时，互信息量达到第1个极小点，所以最佳时间延迟选择s.

采用G-P算法得到的嵌入维数m取1～7时ln C（r）与lnδ的关系图如图2所示.由于m≥4时，图中各条曲线互相平行，其斜率保持稳定不再变化，关联维数趋于饱和阶段，所以嵌入维数选择m＝4.

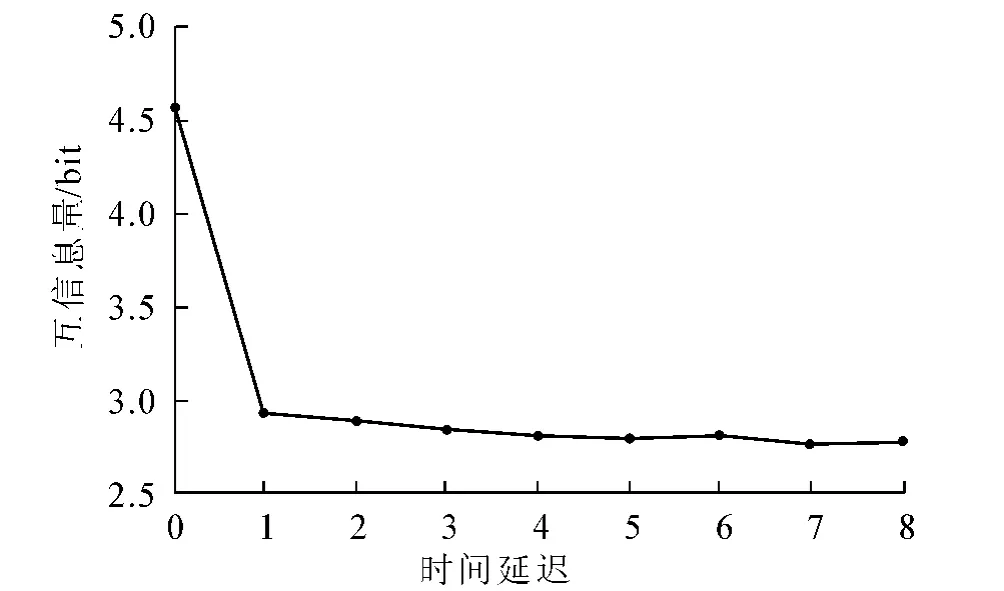
图1 交通流时间序列的互信息量函数

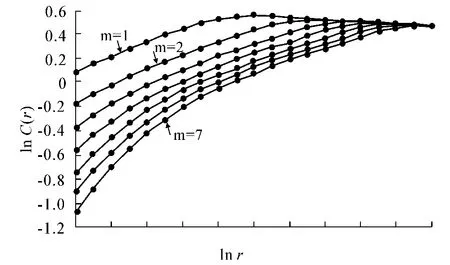
图2 交通流时间序列关联积分与半径的关系

3.2 实测交通流数据混沌特性分析

为了更加直观地反映短时交通流序列的混沌特性，文中同时给出含噪声的Lorenz序列和交通流序列的功率谱图，如图3所示.其中Lorenz混沌时间序列的系统方程为

其中：a＝10，b＝28，c＝8／3；初始化参数x（0）＝12，y（0）＝2，z（0）＝9；采样间隔为0.01s，Lorenz混沌序列的计算方法采用四阶Runge-Kutta法.Lorenz混沌时间序列中加入均值为0信噪比为0dB的高斯白噪声.

对照图3a）和3b）可以看出，低频部分的功率谱都存在连续的宽峰，而高频部分则表现出噪声的特性，表明交通流序列是含有噪声的混沌序列.

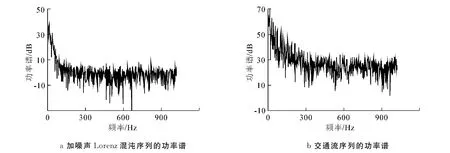
图3 不同时间序列的功率谱

表1给出了无噪Lorenz混沌时间序列和交通流时间序列的最大Lyapunov指数求解结果，其中无噪Lorenz混沌时间序列的系统方程为（2）式所示，Lorenz混沌序列的计算方法和参数设置均与前文一致.从表1可以看出交通流时间序列的最大Lyapunov指数大于零，与无噪Lorenz混沌时间序列的大小相近，且均较小，表明交通流时间序列具有较好的可预测性.

表1 最大Lyapunov指数对比分析

3.3 基于神经网络的模型预测

文中研究所用的交通流数据的采样间隔为10min，共720个采样点数据.预测方法采用前4d的交通流数据作为网络训练样本，最后1天的交通流数据作为测试样本.依据文中前面研究的结果，延迟时间τ＝1，嵌入维数m＝4，所以将720个采样点数据重构为4×716的输入序列矩阵和1×716的输出序列矩阵.其中用于神经网络训练的输入矩阵大小为4×572，输出目标序列矩阵大小为1×572；用于检测神经网络预测效果的输入序列矩阵大小为4×144，输出目标序列矩阵大小为1×144.为了便于快速收敛，首先对采集到的原始数据进行归一化处理，使得数据样本值落在0到1之间.BP神经网络的设置如下：输入层有4个神经元，输出层有1个神经元，隐含层的神经元个数为5，隐含层的激活函数为logsig，输出层的激活函数为purelin，训练函数为trainlm，训练次数为3 000，训练目标值为0.000 1，学习速率为0.1.RBF神经网络的设置如下：网络误差目标为0.000 1，散布常数为1，隐含层神经元个数为25，添加显示的神经元数目为1.

图4，5分别给出了BP神经网络和RBF神经网络对交通流序列进行预测的结果.

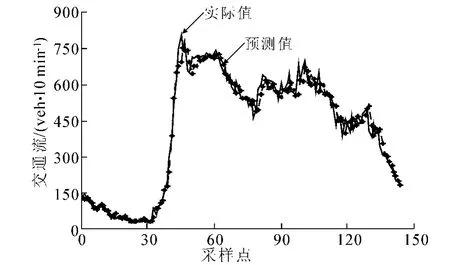
图4 BP神经网路的预测结果

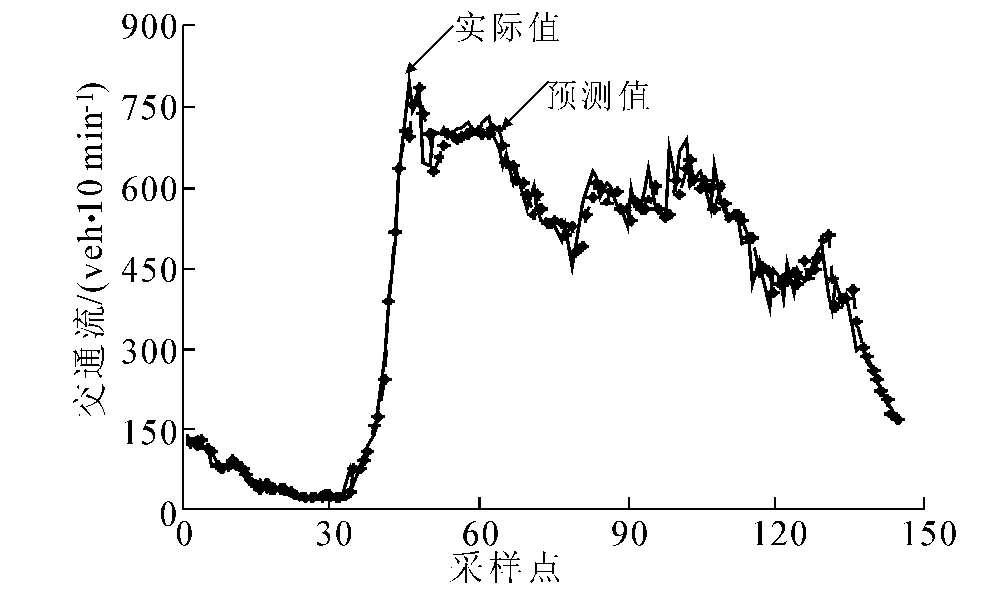
图5 RBF神经网路的预测结果

表2给出了BP神经网络和RBF神经网络对交通流进行预测的误差统计结果.

表2 预测的误差统计

从图4，5可知，无论是采用BP神经网络还是RBF神经网络对交通流进行预测，其预测值曲线和真实值曲线的变化趋势一致，预测值和真实值之间拟合较好.表2表明2种模型的预测结果均能较好反映交通流变化的趋势和规律，预测精度较高，可以满足交通控制和诱导所需要的预测精度.但采用RBF神经网络进行预测时，其训练时间为BP神经网络的37.5%.

4 结语

（1）对实测交通流时间序列分别采用饱和关联维数法和互信息量法进行了嵌入维数m和延迟时间τ的计算，并根据计算结果对交通流时间序列进行了相空间重构.随后分别采用计算最大Lyapunov指数和功率谱分析的方法对相空间重构后的交通流的混沌特性进行了定量和定性分析.结果表明，短时交通流序列是含有噪声的混沌序列，能够对其进行精度较高的预测.

（2）建立了基于BP神经网络和RBF神经网络的交通流预测模型.实验结果表明，2种模型均能够较好的反映交通流变化的趋势和规律，预测精度较高.但RBF神经网络的训练速度更快，性能更好.

［1］ TAKENS F.Determing Strange Attractors in Turbulence［J］.Lecture Notes in Math，1981，89（8）：361－381.

［2］ 吕金虎，陆君安，陈士华.混沌时间序列分析及其应用［M］.武汉：武汉大学出版社，2002：57－80.

［3］ 王海燕，卢 山.非线性时间序列的分析及其应用［M］.北京：科学出版社，2006：33－40.

［4］ 杨 飞.基于回声状态网络的交通流预测模型及其相关研究［D］.北京：北京邮电大学，2012.

［5］ 陈雪平，曾 盛，胡 刚.基于BP神经网络的短时交通流预测［J］.公路交通技术，2008，6（3）：115－117.

［6］ 朱 凯，王正林.精通MATLAB神经网络［M］.北京：电子工业出版社，2010：375－394.

［7］ WANG Jin，SHI Qi-xin，LU Hua-pu.The Study of Short-Term Traffic Flow Forecasting Based on Theory of Chaos［C］／／2005IEEE Intelligent Vehicles Symposium.USA：IEEE Press，2005：869－874.

［8］ 史忠植.神经网络［M］.北京：高等教育出版社，2009：140－155.

（责任编辑 陈炳权）

Analysis and Prediction on the Chaotic Property of Traffic Flow Time Series

LUO Yi
（College of Physics and Information Science，Hunan Normal University，Changsha 410081，China）

The real-teime and procise short-ferm traffic flow forecesting is the key factor for the realizing of traffic control and traffic guidance in the intelligent traffic system.Saturated correlation dimension method and mutual information method are used to calculate embedding dimension and delay time，and the traffic flow time series is reconstructed accordingly in phase space.Wolf method is used to calculate the largest Lyapunov exponent，and the power spectrum of traffic flow time series is analyzed.Results show that the traffic flow series is a chaotic sequence with noise.The prediction models based on BP neural networks and RBF neural networks are applied to pedict traffic flow time series，which shows that the two models both have good prediction effects，with the former having higher prediction accuracy and quicker prediction speed.

embedding dimension；delay time；phase space reconstruction；BP neural networks；RBF neural networks

U495

A

10.3969／j.issn.1007－2985.2013.05.015

1007－2985（2013）05－0060－06

2013－06－15

湖南省教育厅科学研究资助项目（11C0816）

罗 轶（1980－），男，广西陆川人，湖南师范大学物理与信息科学学院讲师，博士生，主要从事移动通信与交通信息处理研究.